同余理论在单循环比赛程序表编排中的应用
2015-10-17杨玲
杨玲
(凉山卫生学校 数理化教研室,四川 西昌 615000)
同余理论在单循环比赛程序表编排中的应用
杨玲
(凉山卫生学校 数理化教研室,四川 西昌 615000)
单循环比赛需要详细确定每1轮的参赛队对阵,应用同余理论可以很好地完成单循环比赛程序表的编排.
同余理论;单循环比赛;程序表;编排
0 引言
所谓单循环比赛,就是所有参加比赛的队都相互比赛1次,最后按照所有比赛过程中胜负场数与得分多少排列名次.这是1种比较公平合理的竞赛方法,在比赛队伍数量不多、竞赛时间充足的情况下多采用这种方法.
假设有N个队参加比赛,当N为奇数时,在每一轮比赛中总有1支队伍要轮空;当N为偶数时就不会出现轮空的情况.为了解决这一问题,可以在N为奇数时人为加进1个队,使比赛队伍数量变为偶数.然后安排一个N+1个队的比赛程序表,在每1轮比赛中,被安排和加进的队就轮空.这样就可以假设有偶数个队进行比赛,并按国内比赛或世界性比赛惯例,给每个队1个编号.
一般国内比赛,各队以上届比赛所取得的名次数作为代号,如第1名为“1”,第2名为“2”,依次类推;世界性比赛则大都采用东道主代号为“1”,上届第1名为“2”,依次类推.这样自然就给加进的队1个最大的编号.并且很容易知道,在单循环比赛中,每个队所要进行的比赛的总场数为N-1,比赛轮次为N-1轮.
为了下面证明需要,先给出有关同余式的一些性质.
引理1[1]同余理论:设0≠m∈Z,a,b∈Z,如果m∣b-a,就称b同余于a模m,记作 b≡a(mod m).
引理2[1](i)a≡a(mod m);
(ii)若b≡a(mod m),则a≡b(mod m);
(iii)若c≡b(mod m),b≡a(mod m),则c≡a(mod m).引理3[2](i)若a≡b(mod m),c≡d(mod m),则a+c≡b+d(mod m);
(ii)若a+b≡c(mod m),则a≡c-b(mod m).
引理4[3]若ac≡bc(mod m),(c,m)=1则a≡b(mod m).
1 比赛程序表推导
现假定x,r∈A={1,2,…,N-1},则可用同余式

来确定在第r轮比赛中,第x队的对手是第y队.
但我们的任务是要使不同的队在每1轮比赛中有不同的对手,让所有参加比赛的队都相互比赛1次.下面就(1)式证明以下几点.

则由(2)(3)式可得
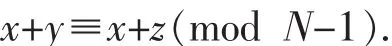
所以y≡z(mod N-1),又y,z∈A,所以y=z.
这就说明了每1个队在每1轮比赛中对手是唯一的.
(二)在每1轮比赛中,若为x队确定的对手是y队,则为y队确定的对手也是x队.
证明 设在第r轮比赛中,x队的对手是y队,y队的对手是z队,且x,y,z∈A,则
由(1)式有

则由(4)(5)式可得
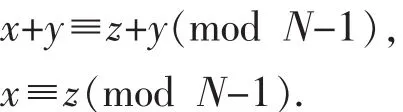
又因为x,z∈A,所以x=z.
即在每1轮比赛中,若为x队确定的对手是y队,则为y队确定的对手也是x队.
(三)每1个队在每1轮比赛中都和不同的对手进行比赛.
证明 设第x队在第r轮和第s轮的对手分别为y,z,且x,r,s∈A,r≠s,则由(1)式有
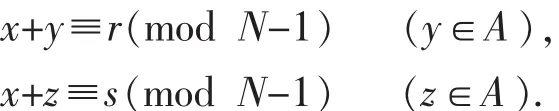
若y=z,则r=s,出现矛盾,所以y≠z.
故每1个队在每1轮比赛中都和不同的对手进行比赛.
但当(1)式中x=y时,这种情况就违反了比赛规则.而事实上,这种情况又是不可避免的,现在就来证明这种情况的存在.
证明 由(1)式有

这里x,r∈A,并且仅有1个这样的x满足(6)式.
若y∈A,也满足(6)式,则2y≡r(mod N-1).
又2x≡r(mod N-1),所以2x≡2y(mod N-1).
因为N-1是奇数,所以(2,N-1)=1,x≡y(mod N-1).
又因为x,y∈A,所以x=y.
即在每1轮比赛中,满足(4)式中的第x队是唯一的.并且很容易知道(6)式在集合A中总有一解为

从而,除了满足(6)式的那个例外的队外,通过(1)式,对集合A中的每1个队,都已经指定了它在第r轮比赛中的对手,而让满足(6)式这个例外的队与第N个队进行比赛.
于是,接下来的任务就是要对这个特殊的第N队进行像(一),(二),(三)的证明,即如下结论.
(四)第N个队在每1轮比赛中,对手x是唯一的.
前面已证明在每1轮比赛中,满足(6)式中的第x队是唯一的.所以第N个队在每1轮比赛中,对手x是唯一的.
(一)每1个队在每1轮比赛中,对手是唯一的.
证明 ∵在第r轮比赛中,对x队确定对手y队,z队,且x,y,z∈A,则
由(1)式有
(五)在每1轮比赛中,若为N队确定的对手是x队,则为x队确定的对手也是N队.
因为让满足(6)式这个例外的x队与第N队进行比赛,所以N队确定的对手是x队,则为x队确定的对手也是N队.
(六)第N队在每,1轮中都和不同的对手进行比赛.
证明 假设在第s轮和第r轮中(s≠r)有

这里x,y,s,r∈A,若x=y,则s≡r(mod N-1).
又因为s,r∈A,所以s=r,出现矛盾,因此x≠y.
即第N队在每1轮比赛中都和不同的对手进行比赛.
以上就证明了(1)式能够使在每1轮比赛中,不同的队有不同的对手,而且在整个比赛中,对于有N个队参加的比赛,各个队的对手均为N-1个队,又比赛总共N-1场,则每两队恰好比赛了1次.这就是单循环比赛,所有参加比赛的队都相互比赛1次.
2 比赛程序表编排
现在用(1)式来安排单循环比赛的程序表.现就一般情况给出这张程序表,即来排一张有N个队参加的单循环赛程序表,这里N为偶数,所要比赛的轮次为N-1轮,即r∈{1,2,…,N-1}.按照(1)式得到的详细单循环赛程序表见表1.
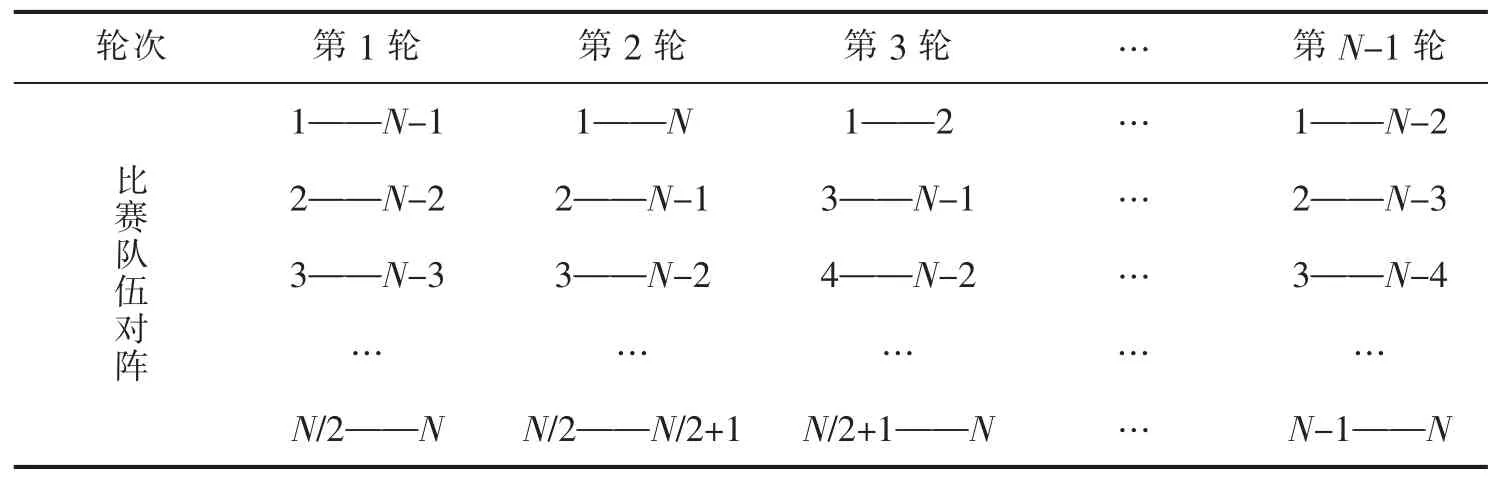
表1 单循环赛对阵表
以上结果表明,同余理论可以很好地应用到单循环比赛程序表的编排中.
[1]闵嗣鹤,严士健.初等数论[M].北京:高等教育出版社,2004.
[2]潘承洞,潘承彪.初等代数数论[M].济南:山东大学出版社,1991.
[3][美]杜德利.基础数论[M].上海:上海科学技术出版社,1980.
(责任编辑 钮效鹍)
Application of Congruence Theory in Round-robin Tournament Schedule
YANG Ling
(Department of Math,Physics and Chemistry,Lianshang Health School,Xichang,Sichuan 615000,China)
A round-robin tournament is a competition in which each contestant meets all other contestants in turn.Congruence theory can be applied to generate the schedule fast and effectively.
congruence theory;round-robin tournament;schedule;arrangement
O156
A
1673-1972(2015)03-0028-03
2015-02-15
杨玲(1982-),女,四川西昌人,助教,主要从事数学教学研究.
