1 m口径非球面主镜面型检测结果分析

孙宁，于帅北，赵天骄，2

（1.中国科学院长春光学精密机械与物理研究所，吉林长春130033；2.中国科学院大学，北京100039）



1 m口径非球面主镜面型检测结果分析

孙宁1，于帅北1，赵天骄1，2

（1.中国科学院长春光学精密机械与物理研究所，吉林长春130033；2.中国科学院大学，北京100039）

介绍了三种常用非球面镜片面型精度的检测方法。在用干涉仪对非球面大口径主反射镜进行检测时，由于使用了辅助平面镜，得到的检测结果并不是主镜的真实面型精度。综合考虑干涉仪测量结果和辅助平面镜面型精度的Zernike多项式，得到了某1m口径抛物面主镜的实际面型精度。

非球面；主反射镜；辅助平面镜；干涉测量；Zernike多项式

引言

在光电经纬仪的望远镜系统中，主反射镜是光电测量设备的关键部件，其面型精度对光学系统的成像质量起着决定性的作用。

非球面主镜相对于球面主镜具有更大的自由度和灵活性以及更多的设计变量，应用于光学系统可以使用更少的元件数量来实现更高的系统性能，有效地校正各种相差，改善像质。随着光电经纬仪望远系统的应用需求不断提高，要求主镜具有更高的面型精度、更大的口径。对非球面主镜面型误差进行检测也成为重要研究内容。

尽管非球面光学元件在设计和使用性能上具有诸多优点，但在应用规模上远不如平面和球面光学元件，原因主要在于非球面光学元件的检测难度要远远大于平面和球面光学元件。现对常见的非球面镜片的面型检测技术做以介绍，并对某型光电经纬仪1 m口径主镜的检测结果进行分析［1-2］。

1　常见非球面面型检测方法

非球面主镜的面型检测技术可以分为接触式检测和非接触式检测两大类。

1.1接触式检测

最常见的接触式检测是三坐标检测法，即利用三坐标测量机，直接测量出非球面表面各点的三维坐标值，得到非球面表面形状误差。这种测量方法虽然原理简单，但是测量效率低下，而且属接触式测量，易对被测反射面造成磨损。

1.2非接触式测量

1）补偿镜法。

补偿镜法是一种以补偿镜作为辅助元件，通过完全补偿非球面的法向像差产生与理想非球面形状一致的波前，进而对非球面进行面型检测的技术。其原理光路如图1所示。

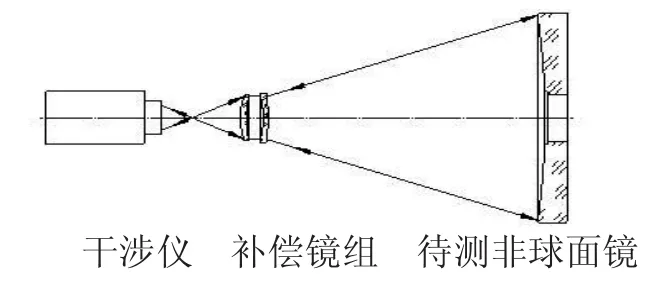
图1　补偿镜法检测非球面光路图

一般来说，补偿镜法检测凹面镜时所用的补偿镜口径相对被测面来说要小得多，容易加工到很高的精度。但是仍然有一些不足，比如设计难度大，测量中存在难以取出的装调和制造误差，针对不同参数的非球面需要专门设计与之对应的补偿镜从而不具备通用性等。

2）无像差点法。

无像差点法利用了二次曲面光学共轭点的性质，借助平面或球面镜的辅助完成对非球面面型的检测，合理设计辅助反射镜的尺寸及位置，就可以与待测二次曲面组成自准直系统，进而利用干涉仪完成零位检测。

如下页图2所示，由焦点处点光源发出的光经抛物面反射后成为平行光，再由辅助平面反射镜反射后沿原路返回干涉仪，形成零位检测。

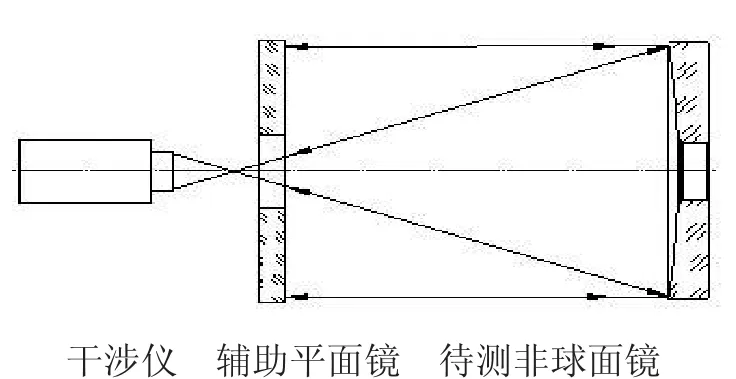
图2　无像差点法检测抛物面光路图

虽然无像差点法存在一些不足，如当被测二次曲面口径增大时，辅助反射镜的尺寸也相应变大，增大了加工成本；对助反射镜的面型精度和装调精度要求很高等，但是无像差点法测量方便，检测精度也很高，是二次曲面面型检测的一种常用方法［2-9］。

本文采用无差像点法对某型号经纬仪1m口径抛物面主反射镜的反射面面型精度进行检测，和辅助反射镜已知面型分别进行Zernike拟合，从而分离出主镜本身的面型精度，为进一步的分析提供数据和依据。

用Zernike多项式的协方差矩阵的线性变换来直接求解多项式系数的方法不需经过正交化过程，很适合于编写拟合过程的计算机程序［10-12］。

2　辅助平面镜

本次检测使用的平面镜外径Φ1 050mm，中心有效直径Φ160mm，厚度160mm，材料为微晶玻璃。支承方式为吊带支承。其面型精度RP=0.020 6 λwv=λwv/48.5=13.04 nm（λwv=632.8 nm）。检测干涉图如图3所示。

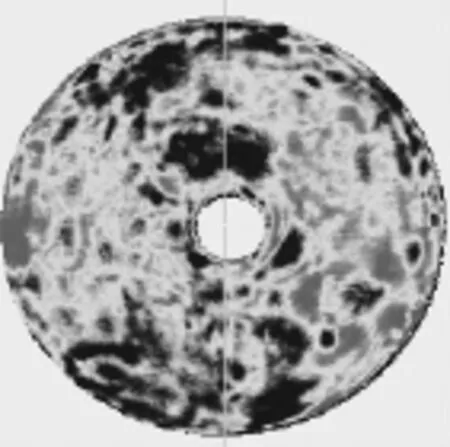
图3　干涉仪对辅助平面镜面型检测

同时可以得到辅助平面镜面型精度的36项Zernike拟合公式：

3　主镜面型精度检测

本文被测主镜材料为微晶玻璃，有效通光口径Φ1 000mm，中心有效直径Φ200 mm，边缘厚度140mm，反射面为抛物面。支承状态为安装在主镜室中。

使用4D干涉仪及3中辅助平面镜，按2.2（2）中无像差点方法对其进行检测，得到如图4所示干涉图。其面型精度RP=0.029 6λwv=λwv/33.8=18.73 nm（λwv=632.8 nm）。

同时可以得到主镜检测面型精度的36项Zernike拟合公式：

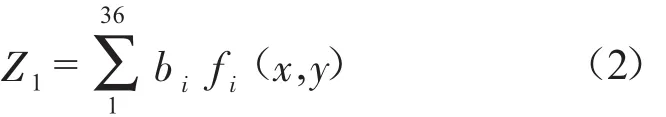
图4　干涉仪对支承系统中主镜面型检测

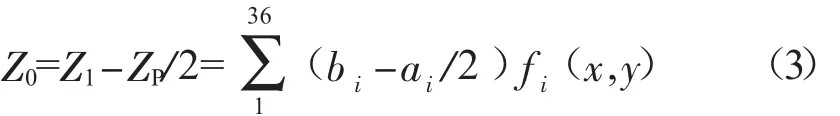
其面型精度R0=0.024 5λwv=λwv/40.8=15.5 nm（λwv=632.8 nm）。面型云图如图5所示。

4　主镜实际面型

使用无像差点法检测主镜，其结果包含了辅助平面镜带来的影响。如果要对主镜在支承系统中的不同状态进行更精确分析，就要将检测结果中辅助平面镜的影响排除。

由于检测时光线在主镜上进行了两次反射，在辅助平面镜上进行了一次反射，所以主镜实际面型的36项Zernike拟合公式为：

图5　支承系统中主镜实际面型云图

5　误差分析

1）36项Zernike拟合公式排除了各高频项，与实际面型不可能完全一致，会使分析结果产生一定误差；

2）干涉仪检测主镜和平面镜面型精度时，取的是多组检测的最优值，与真值之间亦存在微小误差。

6　结论

1）使用4D干涉仪及3中辅助平面镜，按2.2（2）中无像差点法对某1m口径抛物面主镜面型精度进行检测，得到如图4所示干涉图及面型精度（RP=0.0296λwv）。

2）根据干涉仪检测结果对辅助平面镜和被测主镜面型精度分别进行拟合，得到36项Zernike拟合公式，见公式（1）、公式（2）。

3）根据公式（3），得到排除辅助平面镜影响后的支承系统中主镜实际面型的36项Zernike拟合公式，以及面型精度（R0=0.024 5λwv）和如图5示面型云图。

［1］谢高容.非球面镜片面型检测技术综述［J］.光学仪器，2007，29（2）：87-90.

［2］师途，杨勇英.非球面光学元件的面形检测技术［J］.中国光学，2014，7（1）：26-46.

［3］张坤领，林彬，王晓峰.非球面加工现状［J］.组合机床与自动化加工技术，2007（5）:1-5；10.

［4］张金平.夏克-哈特曼波前传感器检测大口径非球面应用研究［D］.长春:中国科学院长春光学精密机械与物理研究所，2012.

［5］王孝坤.激光跟踪仪检验非球面面形的方法［J］.光子学报，2012，41（4）：379-383.

［6］卢文川，张金平，等.Shack-Hartmann波前传感器非零位在轴检测离轴非球面反射镜［J］.光学技术，2012，38（4）:410-414.

［7］雷柏平，伍凡，陈强.大口径非球面Ronchi光栅测量方法［J］.光电工程，2007，34（5）:140-144.

［8］SELKE L A.Theoretical elastic deflections of a thick horizontal circular mirror on a double-ring support［J］.Appl Opt，1970，9（6）:1 453-1 456.

［9］NELSON JE，LUBLINER J，MAST T S.Telescope mirror supports: plate deflections on point supports［J］.SPIE，1982，333（12）:212-228.

［10］刘月爱.条纹分析中一种简单的Zernike多项式拟合方法［J］.光学学报，1985，5（4）:368-373.

［11］MACK B.Deflection and stress analysis of a 4.2-m diameter primary mirror of an altazimuth-mounted telescope［J］.Appl Opt，1980，19（6）:1 000-1 010.

［12］WILSON R N.Reflecting telescope optics Ⅱ，manufacture，testing，alignment，modern techniques［M］.Berlin:Springer，1999:242-259.

（编辑：姚欢）

Accuracy Analysis of Primary Mirror with 1m-aperture

Sun Ning1，Yu Shuaibei1，Zhao Tianjiao1，2
（1.Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun Jilin 130033；2.University of Chinese Academy of Sciences，Beijing 100039）

Three common kinds of aspheric lens surface testing methods are introduced.When the large diameter aspheric primary mirror is tested by the interferometer，the obtained result don't show the actual accuracy of the primary mirror due to the use of auxiliary plane mirror.Taking the test results of interferometer and the Zernike polynomials for the accuracy of the auxiliary plane mirror into consideration，we get the real accuracy of a parabolic primary mirror with 1meter-aperture.

aspheric；primary mirror；auxiliary plane mirror；interferometer；Zernike polynomials

TH745

A

2095-0748（2015）23-0035-03

10.16525/j.cnki.14-1362/n.2015.23.15

2015-10-29

孙宁（1974—），男，吉林辽源人，硕士，毕业于中科院长春光机所，现就职于中科院长春光机所，副研究员，主要从事主镜支撑系统研究。