平板折叠桌的参数设计
2015-10-17涂冰贤蔡晨瑶李韶伟
涂冰贤,蔡晨瑶,林 晶,李韶伟
(台州学院 数学与信息工程学院,浙江 临海 317000)
0 引言
创意平板桌[1](the Rising Side Table)是由荷兰设计师Robert van Embricqs设计的一种可折叠成平板的桌子,桌面呈圆形,桌腿随着铰链的活动可以平摊成一张平板,见图1。桌腿由若干根木条组成,分成两组,每组各用一根钢筋将木条连接,钢筋两端分别固定在桌腿各组最外侧的两根木条上,并且沿木条有空槽的位置以保证滑动的自由度。桌子外形由直纹曲面构成,造型美观[2]。
依据2014年全国大学生数学建模赛题[2],考虑创意平板折叠桌的动态变化过程,设计加工参数(桌腿木条开槽的长度、桌脚边缘线(见图4)、平板尺寸、钢筋位置)等要求,本文研究如下问题:
问题1.对于给定尺寸的长方形平板、木条宽度以及折叠后的桌高,建立模型描述此折叠桌的动态变化过程,并给出相关加工参数。
问题2.对于给定的桌高和桌面直径,综合考虑各项设计因素,讨论折叠桌的最优设计加工参数。
问题3.对于给定的桌面形状,根据所建立的模型设计创意折叠桌。

图1 折叠桌的动态过程
1 模型假设
a.假设长方形平板切割后相邻木条之间紧密排列,没有空隙;
b.假设切割点都位于各个木条宽的中点处,见图2所示;
c.假设钢筋在开槽中可自由移动,无摩擦;
d.假设开槽上下两端预留木条的最小长度相同;
e.在不涉及体积的情况下,将钢筋、木条视为线段(同理忽略桌面厚度)。
2 模型建立与求解
2.1 问题1的分析与求解
第一步:确定切割点为木条宽的中点。
第二步:假设桌面单侧切割木条n根,长方形平板的长和宽分别为L,W。如图2所示,以圆形桌面的中心位置为坐标原点建立三维坐标系,令木条切割点对应的横坐标从上至下依次为x1,x2,…,xk,xn,可得

从而确定其第k根木条的桌脚长为

第三步:当折叠桌达到最佳稳固状态时,根据桌高和第一条桌脚长满足的正弦关系确定桌脚偏离平面位置的最大角θm。由折叠桌的初始状态得到第k根木条开槽最上方位置到铰链的距离dk1,运用余弦定理得到折叠桌在稳固状态时第k根木条开槽最下方位置到铰链的距离dk2,那么第k根桌腿木条开槽的长度为



图2 切割点的位置

图3 第k根木条稳定状态的截面图
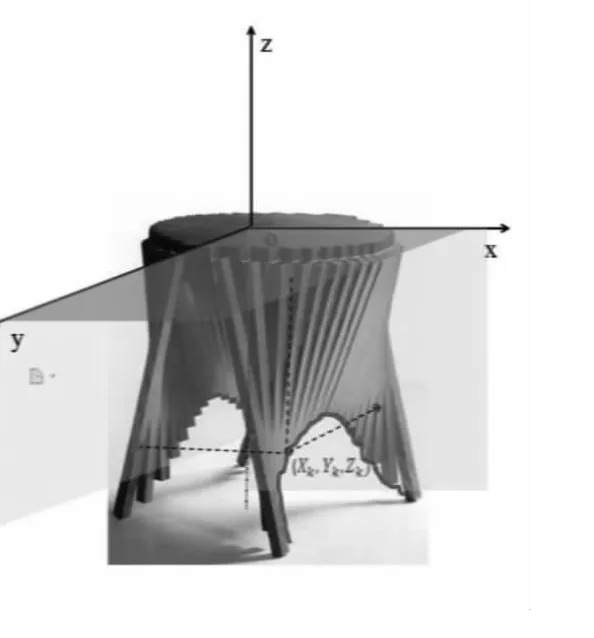
图4 桌脚边缘线的三维坐标系
由Matlab编程可得折叠桌从初始平板状态到稳固状态的折叠过程中,各个桌脚运行轨迹图,见图5。
同时计算出xk、桌脚长度lk、槽长△dk,进而描述出达到稳固状态时桌脚边缘线图(见图6)。
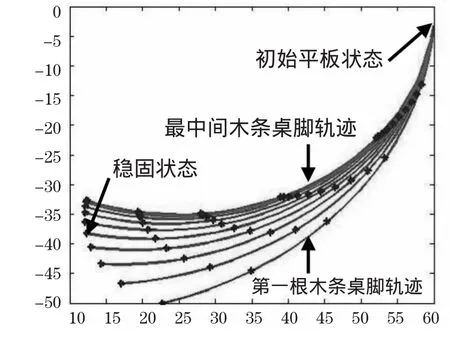
图5 折叠过程中桌脚运行轨迹图
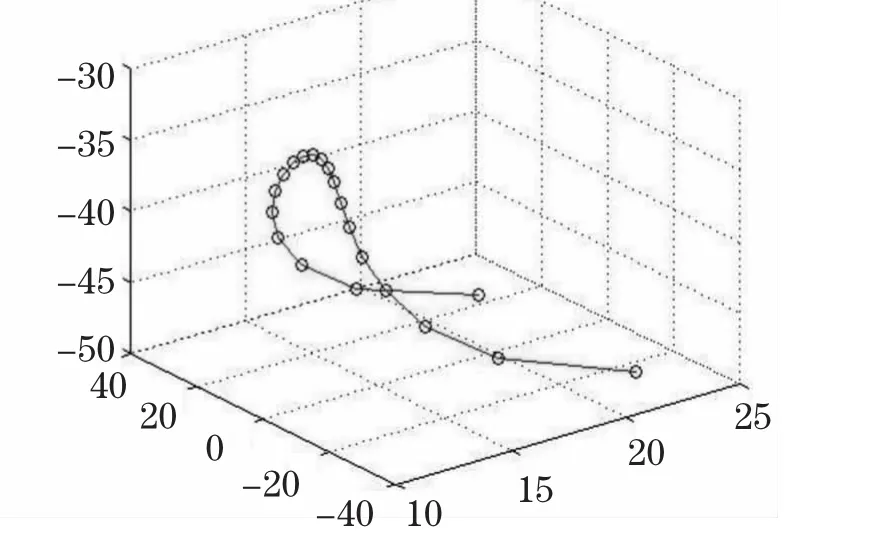
图6 稳固状态桌脚边缘线图
2.2 问题2的分析与求解
2.2.1 相关指标的分析
由于折叠桌的设计要做到稳固性好、加工方便、用材最少,而每一项指标都较为抽象,因此需要将其数值化,用具体的数值衡量其设计的优劣。
加工方便的分析:以长方形木板的切割条数n来衡量折叠桌的加工方便程度,n越小,加工越方便。
用材最少的分析:由于长方形木条的厚度不可忽略,通过折叠桌的体积大小衡量其用材的多少。
2.2.2 问题二的算法设计
在此基础上最优的加工参数设计过程如下:
第一步:设定初始桌面直径W,桌高H,木条n根,给定一个初始的桌脚倾斜角θ,可得

第二步:通过稳固率η,可得到长方形木板的长
L=2Hcosθ+2x1.
第三步:设定开槽上下两端预留木条的最小长度都为Sk,由此得到最长桌脚的开槽最上方位置到铰链的距离dk1和开槽最下方位置到铰链的距离dk2,确定钢筋的大致位置,见图8。
商务酒店设计中的客房设计应为旅客提供一个私密的、放松的、舒适的空间,浓缩了休息、私人办公、娱乐、商务会谈等诸多使用要求的功能性空间,该部分是客户入住后的重要的活动部分,在设计方面必须全面考虑美感与舒适程度,应该通过细节来展现出中式元素,保证客户能够在入住过程中体验心灵的休息。

图7 有效支撑面积

图8 初始状态桌面的俯视图
第四步:根据最初设定的木板长度L及其他参数可计算得到的木板长度L’为

进一步可由差值△L=L-L’修正钢筋的位置。
第六步:在得到稳固状态时桌脚倾斜角θm与木条根数n的情况下,相当于得到了与问题一相同的条件,测试不同的n与H的值,对比即可得到最优设计加工参数(长方形平板尺寸、钢筋位置、开槽长度)。部分测试数据木条的根数n、木板的长度L以及折叠桌的体积V如表1所示。

表1 问题2的测试结果
最优设计加工参数如下:
平板尺寸:L=85.53cm,W=80cm,h=3cm;
钢筋的位置在第十根桌腿到铰链6cm处;
开槽的长度见表2。

表2 开槽的长度cm
2.3 问题3的分析与求解
对于任意给定的桌面形状,考虑稳固性和材料利用方面的因素,假设桌面单侧木条数量n和桌腿与地面所成的角为90°,则桌子所对应的高为

由此可根据客户对桌面形状和高度的要求确定桌面切割的木条数量n和所需长方形木板的长度L。如图9所示,利用目标逆推法,进一步可构建从特殊到一般的平板桌模型。

图9 任意桌面切割木条前的预设定过程示意图
下述以对“半八卦桌”(见图10)为例进行分析并建立桌脚架构模型,设计创意折叠桌。
第一步:根据图9能确定各组桌腿投影到地面上的点,再由桌脚边缘线的大致形状确定桌面大致形状,经过分段切割之后取出其中任意一个独立弧线,建立如图11所示的坐标系。
第二步:利用图像数字化的方法,得到“半八卦桌”桌面对应最短长度的半桌木条长度x1,同理依次求出 x1,x2,…,xk,xn。
第三步:由问题2的方法确定θ和k。利用Matlab编程得到“半八卦桌”的折叠过程示意图,见图12,并给出最优设计加工参数。
第四步:由模型得到另外两组创意平板折叠桌的设计加工模型,见图13。
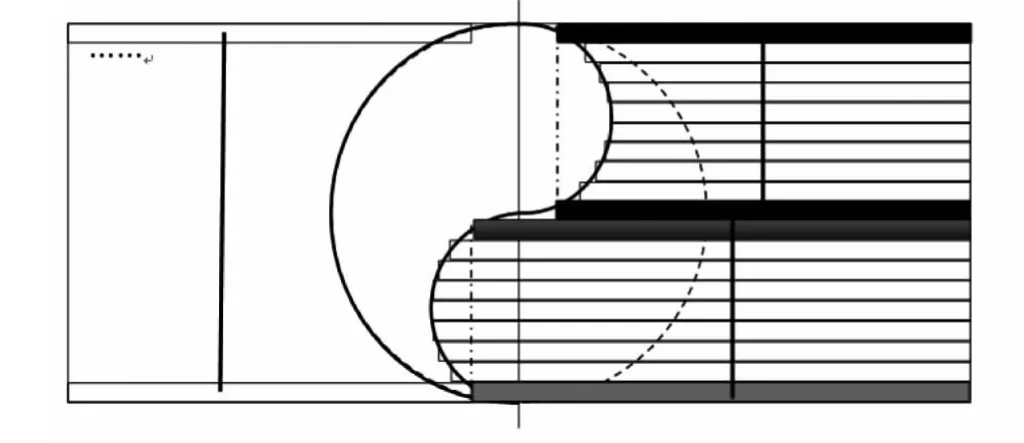
图10 “半八卦桌”的桌面分割图

图11 局部凸曲桌面平铺示意图

图12 “半八卦桌”的折叠过程示意图

图13 (规则桌面的)创意平板折叠桌举例示意
3 模型检验及评价
灵敏度检验发现加工参数lk,dk1,dk2等结果与桌高H和桌脚偏离平面位置的角度θ等数据变化并不敏感;模型1和模型2都具备很强的实际可操作性等优点。
(1)模型具有较强的可推广性,给定任意长方形平板尺寸和桌高,通过问题1模型即可控制桌脚动态过程和开槽长度。
(2)综合考虑了折叠桌的多个优化目标,任意给定桌高和桌面直径,由问题2模型可得到最优的设计加工参数。
当然本模型也存在着如下不足:
(1)测试所取的桌高和木板厚度的数据有限,得到的结果的最优性有待理论验证。
(2)问题3中“半八卦桌”的参数设计,考虑到桌面厚度、加工误差等因素还有待调整。
4 结束语
本文综合考虑创意平板折叠桌的稳固性、用料最少、加工方便等因素,解决了创意平板折叠桌加工参数的最优设计问题,给出了桌脚边缘线的动态变化结果。模型简洁可靠。进一步地,以“半八卦桌”为例,构建从特殊到一般的桌脚架构模型,给出了一般封闭曲线桌形的桌脚架构条件,并给出了一些以基本图形为桌形的折叠桌动态变化过程的仿真示意图形。
本文的模型可进一步考虑木条厚度,并给出非对称的桌面形状的相应设计加工参数,使模型更具普遍性。
[1]Caroline Williamson.rising-side-table-by-robert-van-embricqs[EB/OL]. (2012-02-07)[2015-3-10].http://design-milk.com/rising-side-table-by-robert-van-embricqs/.
[2]2014 年全国大学生数学建模竞赛赛题 B 题[EB/OL]. (2014-09-11)[2015-3-10].http://www.mcm.edu.cn/html_cn/block/c61dfec317d7a5bd9b2b8efed81c8af3.html.
[3]张智丰.数学实验[M].北京:科学出版社,2008:36.
[4]王正林,刘明.精通MATLAB7[M].北京:电子工业出版社,2007:182.
[5]卓金武,魏永生.MATLAB在数学建模中的应用[M].北京:北京航空航天出版社,2001:93.
