SweedlerHopf代数上Green环的自同构群

贾婷婷，苑呈涛，李立斌

（扬州大学数学科学学院，江苏 扬州225002）

SweedlerHopf代数上Green环的自同构群

贾婷婷，苑呈涛，李立斌*

（扬州大学数学科学学院，江苏 扬州225002）

假设H2是特征为0的代数闭域k上的Sweedler四维Hopf代数，并用r（H2）表示H2的Green环，证明了r（H2）的自同构群Aut（r（H2））同构于Klein四元群.

自同构群；Green环；SweedlerHopf代数

环与代数的自同构是代数学领域最经典的研究问题之一.对于给定的环或代数，如何刻画其自同构群目前还没有统一的方法和技巧.Dicks［1］，Yu［2］，Drensky［3］等在多项式代数的自同构，特别是2个变元的多项式代数（环）方面开展了一些有意义的研究.Alev等人［4］和Artamonov［5］证明了当q不是单位根时量子平面kq（x，y）=k［x，y］/（xy-qyx）以及量子化包络代数Uq（sl（2））的自同构.朱美玲等［6］得到当q不是单位根时量子群Uq（fm（K））的同构与自同构分类.近年来，Green环的研究日渐兴起.Chen等［7］确定了Taft代数Hn（q）的Green环r（Hn（q））的生成元和生成关系.Li等［8］得到了广义TaftHopf代数Hn，d的Green环r（Hn，d）的结构及其所有幂零元的表达式.本文拟利用r（H2）的生成元和生成关系提出r（H2）的自同构群，并证明其自同构群Aut（r（H2））同构于Klein四元群K4.

1　预备知识

设正整数n，d≥2且d|n，q是d 次本原单位根.Radford［9］定义了Hopf代数Hn，d=Hn，d（q）由g和h 生成，且满足gn=1，hd=0，hg=qgh.Hn，d的余乘法Δ、余单位ε和反极元S 分别表示为

注：dimHn，d=dn，｛gihj|0≤i≤n-1，0≤j≤d-1｝是Hn，d的一组PoincareBirkhoffWitt（PBW）基.当d=n时，Hn=Hn，n为n2-维Taft（Hopf）代数［10］；因此，将Hn，d称为广义TaftHopf代数［11］.当n=2时，H2为Sweedler四维Hopf代数.

Hopf代数上的Green环 设H是域k上有限维Hopf代数，有限维H-模V的同构类记为［V］. 设a（H）表示所有［V］生成的自由Abel群，在a（H）上定义乘法［M］［N］=［M⊗N］，则a（H）是环.该环模去所有关系式［M⊕N］=［M］+［N］所得商环称为Hopf代数H的Green环（表示环），记作r（H）.

定理1［7］771，［8］280设Z［y，z］是Z 上关于变量y和z 的多项式代数.Hn，d的Green环r（Hn，d）同构于Z［y，z］/I，式中I为Z［y，z］的理想且由多项式yn-1，（z-ym-1）Fd（ym，z）生成，其中m=n/d.Fd（ym，z）是广义Fibonacci多项式，满足Fs+2（y，z）=zFs+1（y，z）-yFs（y，z），s≥0；F0（y，z）=0；F1（y，z）=1.

推论2 H2的Green环r（H2）同构于Z［y，z］/I，式中I=（y2-1，z2-yz-z）.

2　主要结果

记Aut（r（H2））表示Sweedler四维Hopf代数H2的Green环r（H2）的自同构群.对任意H2的Z-线性变换f，记Af，|Af|分别为线性变换对应的系数矩阵和该系数矩阵的行列式.

设ε，σ，τ，φ是r（H2）上的Z-线性映射，其中ε是恒等映射，σ，τ，φ分别由下式确定：

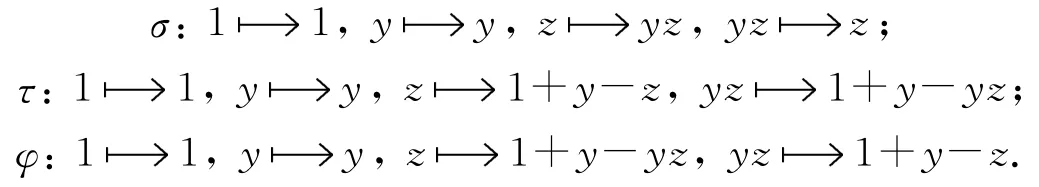
易证ε，σ，τ，φ是r（H2）的自同构，且στ=φ，σ2=τ2=φ2=ε，故｛ε，σ，τ，φ｝是Aut（r（H2））的子群且同构于Klein四元群K4.

命题3 设f是r（H2）的自同构，则f（y）=y或f（y）=-y.

证明 因f是r（H2）的自同构，且y2=1，故（f（y））2=1.

设f（y）=a1+a2y+a3z+a4yz，ai∈z（1≤i≤4），则（a1+a2y+a3z+a4yz）2=1.有a21+a22+ 2a1a2y+（a23+a24+2a1a3+2a2a4+2a3a4）z+（a23+a24+2a1a4+2a2a3+2a3a4）yz=1，可得方程组

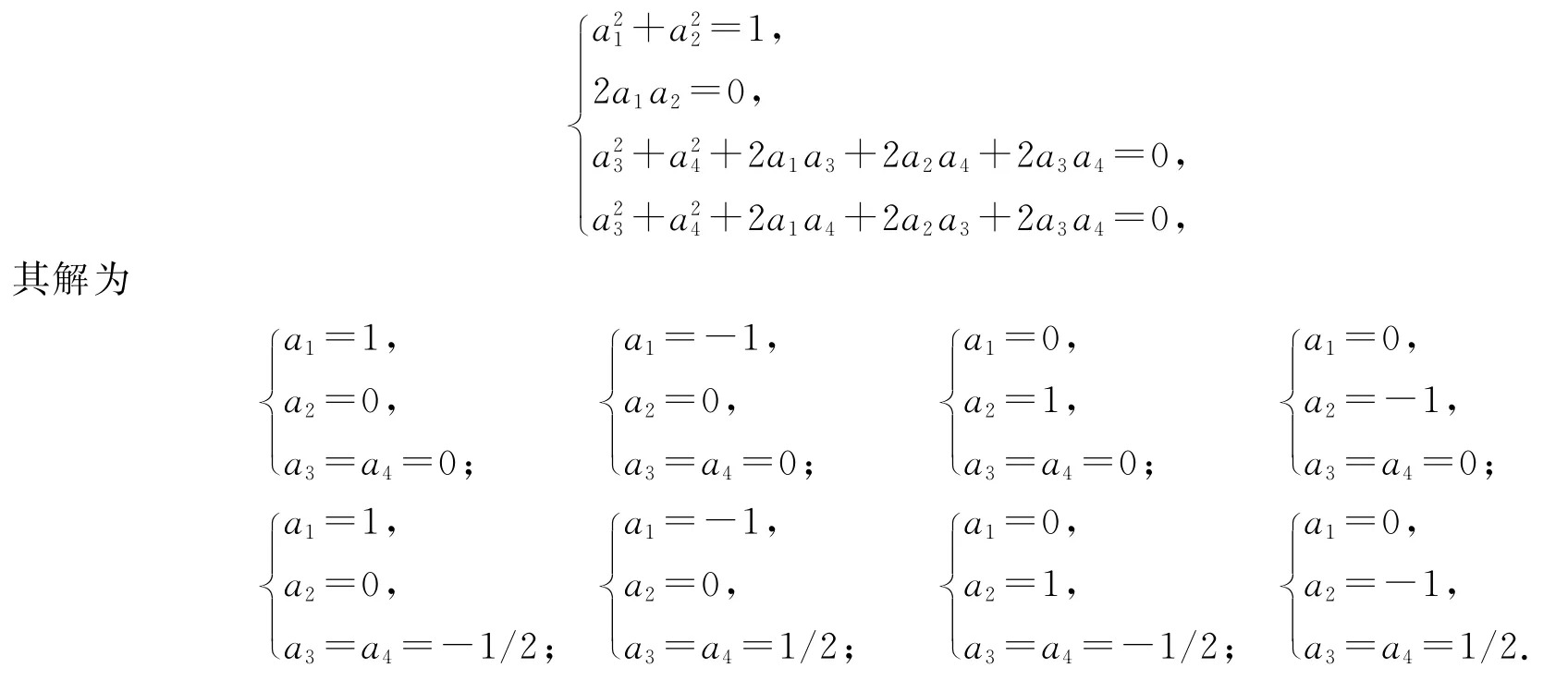
由于a1，a2，a3，a4∈z，f（y）≠1且f（y）≠-1，故只有a1=0，a2=±1，a3=a4=0符合条件，即f（y）=y或f（y）=-y.

根据英语语言文学学科的特点，结合新《国标》和内蒙古科技大学人才培养目标及地方区域对英语人才的需求，通过拓展实习基地、鼓励科研创新和丰富第二课堂等活动增强学生的语言运用能力，培养其研究能力和创新能力，提高综合能力和全面素质，以便更好地培养出国际视野宽阔、语言基本功扎实、创新能力强的高素质英语人才。

命题4 设f是r（H2）的自同构，且f（y）=y，则f∈｛ε，σ，τ，φ｝.

证明 由z2=yz+z得

（f（z））2=f（z2）=f（yz+z）=f（yz）+f（z）=f（y）f（z）+f（z）=［f（y）+1］f（z）=（1+y）f（z）. 设f（z）=b1+b2y+b3z+b4yz，有

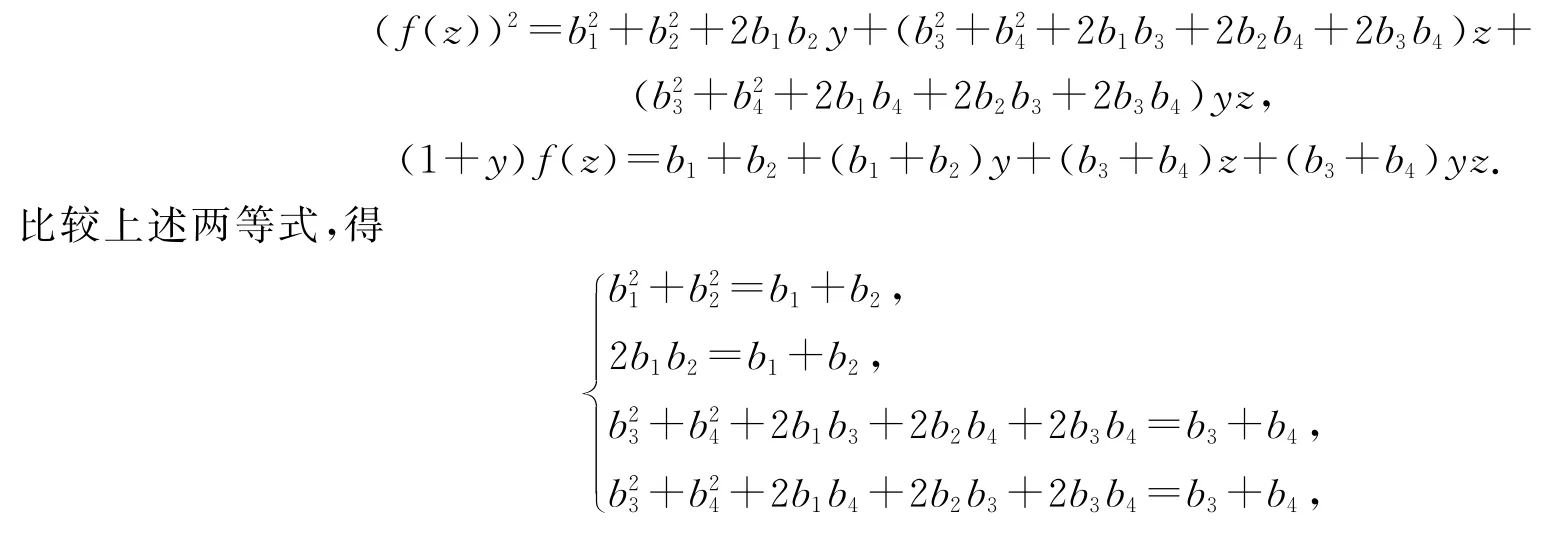
情形1 若f（z）=bz-byz，则f（yz）=-bz+byz.

情形2 若f（z）=bz+（1-b）yz，则f（yz）=（1-b）z+byz.

情形4 若f（z）=1+y+bz-（1+b）yz，则f（yz）=1+y-（1+b）z+byz.

综上可得f∈｛ε，σ，τ，φ｝.

定理5 设Aut（r（H2））是r（H2）的自同构群，则Aut（r（H2））≅K4.

证明 设f是r（H2）的自同构，则当f（y）=-y 时，有f（z）=1-y（证明过程同命题4），因f（z）=1-y=f（1+y），故不成立.由命题3，4知f（y）=y且f∈｛ε，σ，τ，φ｝，故Aut（r（H2））=｛ε，σ，τ，φ｝≅K4.

［1］DICKS W.Automorphisms of the polynomial ring in two variables［J］.Publ Sec Mat Univ Autonoma Barcelona，1983，27（1）：155-162.

［2］YU Jietai.Recognizing automorphisms of polynomial algebras［J］.Mat Contemp，1998，14：215-225.

［3］DRENSKY V，YU Jietai.Automorphisms of polynomial algebras and dirichlet series［J］.J Algebra，2009，321（1）：292-302.

［4］ALEV J，CHAMARIE M.Dérivations et automorphismes de quelques algèbres quantiques［J］.Commun Algebra，1992，20（6）：1787-1802.

［5］ARTAMONOV V A.Quantum polynomial algebras［J］.J Math Sci，1997，87（3）：3441-3462.

［6］朱美玲，沙凯平.量子群Uq（fm（K））的同构与自同构［J］.扬州大学学报：自然科学版，2011，14（3）：6-8，12.

［7］CHEN Huixiang，van OYSTAEYEN F V，ZHANG Yinhuo.The Green rings of Taft algebras［J］.Proc Amer Math Soc，2014，142（3）：765-775.

［8］LI Libin，ZHANG Yinhuo.The Green rings of the generalized Taft Hopf algebras［J］.Contemp Math，2013，585：275-288.

［9］RADFORD D E.On a coradical of a finite-dimensional Hopf algebra［J］.Proc Amer Math Soc，1975，53（1）：9-15.

［10］TAFT E J.The order of the antipode of finite-dimensional Hopf algebra［J］.Proc Nat Acad Sci，1971，68（11）：2631-2633.

［11］CHEN Xiaowu，HUANG Hualin，YE Yu，et al.Monomial Hopf algebras［J］.J Algebra，2004，275（1）：212-232.

The automorphism group of Green ring over Sweedler Hopf algebra

JIA Tingting，YUAN Chengtao，LI Libin*
（Sch of Math Sci，Yangzhou Univ，Yangzhou 225002，China）

Let H2be the Sweedler’s 4-dimensional Hopf algebra over a fixed algebraically closed field k of characteristic 0，where r（H2）denotes the Green ring of H2.In this paper，it is shown that the automorphism group of the Green ring r（H2）is isomorphic to the Klein four group K4.

automorphism group；Green ring；Sweedler’s Hopf algebra

O153.3；O152.2

A

1007-824X（2015）02-0008-04

（责任编辑 秋 实）

2014-11-11.*联系人，E-mail：lbli@yzu.edu.cn.

国家自然科学基金资助项目（11471282）；高等学校博士点基金资助项目（20123250110005）.

贾婷婷，苑呈涛，李立斌.SweedlerHopf代数上Green环的自同构群［J］.扬州大学学报：自然科学版，2015，18（2）：8-11.