分布式发电系统中并网逆变器的控制策略研究

吴春秋，唐慧妍

（1.海军驻上海江南造船（集团）有限责任公司 军事代表室，上海 201913; 2.中国船舶重工集团公司第七一一研究所，上海 201108）

分布式发电系统中并网逆变器的控制策略研究

吴春秋1，唐慧妍2

（1.海军驻上海江南造船（集团）有限责任公司 军事代表室，上海 201913; 2.中国船舶重工集团公司第七一一研究所，上海 201108）

本文针对于LCL型三相并网逆变器的控制策略进行展开，重点分析三相并网逆变器在不同坐标系下的控制特性，最后基于SABER软件搭建10kW系统进行仿真验证。

分布式发电系统；LCL；并网逆变器

0 引言

随着能源危机与环境污染问题日益严峻，以太阳能、风能为代表的可再生能源以其无污染、资源无枯竭等优势将在未来能源格局中扮演重要角色。基于可再生能源的分布式发电系统(Distributed generating system，DGS)与环境相兼容，发电方式灵活，可满足用户的特殊需求，可广泛应用于偏远地区供电。分布式发电系统与集中供电系统结合将形成一个高效，灵活的电力系统，提高了可再生能源的利用率，可有效改善电力系统的供电可靠性和提高供电系统容量[1]。

分布式发电系统的组网方式多种多样，通常按照汇流母线的类型可以分为三类：基于直流母线的组网方式，基于交流母线线的组网方式和基于混合母线的组网方式。基于直流母线的组网方式以其控制简单，扩容方便，易于实现独立/并网双模式运行等优势成为中小容量的分布式发电系统的首选方案。

并网逆变器作为DGS与电网的接口设备，直接影响入网电能质量。通常三相并网逆变器按照滤波器结构划分由L型和LCL型。相比于L型滤波器，LCL滤波器高频衰减特性更好，在获得同样的控制效果时，LCL滤波器的体积更小，因此，更适合大功率场合。

三相并网逆变器是一个多变量、高阶、相互耦合的系统，采用坐标变换来可以减少系统的阶数。基于同步旋转d-q坐标变换，系统的控制量为直流量，使用传统的PI调节器即可获得零稳态误差的控制效果，但LCL型三相并网逆变器在d-q坐标系下存在耦合，要精确设计控制系统，需要对系统解耦。基于静止α-β坐标变换，三相并网逆变器可以等效为两个单相并网逆变器，系统在α轴和β轴上相互独立，不存在耦合，但是α-β坐标系下，系统控制量仍为交流量，因此，系统不易实现零稳态误差控制。本文重点讨论d-q及α-β坐标系下并网逆变器的控制特性，分析d-q坐标系下的耦合量对系统性能的影响以及合理的解耦方式，基于SABER仿真平台，搭建10kW系统，并进行仿真验证。

1 LCL型并网逆变器的数学模型

LCL型并网逆变器主电路拓扑如图1所示。选择电感L1和L2的电流，以及电容电压为状态变量，即可得到系统的状态方程为：

式中，k=a、b、c。由于三相三线制系统要满足三相电流之和为0，因此三相之间会相互耦合。通常，通过abc/dq或abc/αβ坐标变换，使系统降阶[2,3]。

图1 LCL型并网逆变器

通过abc/dq坐标变换后，系统状态方程为：

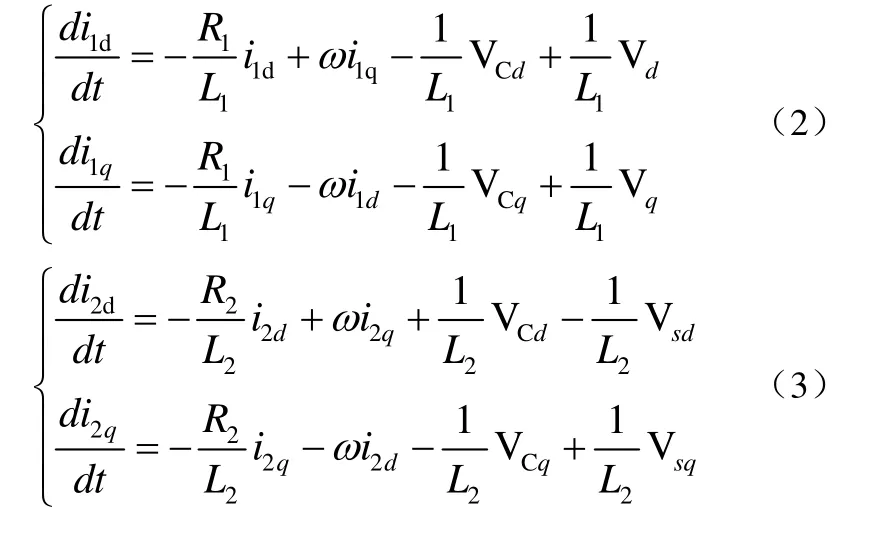
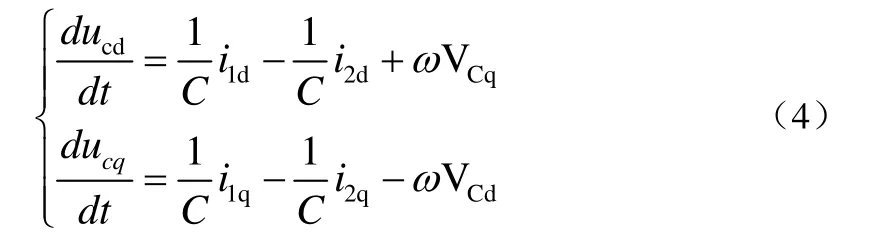
通过abc/αβ坐标变换后，系统状态方程为：

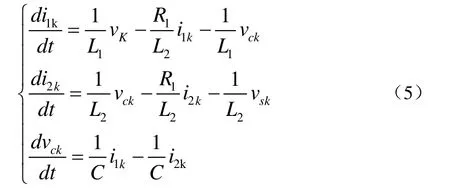
式中，k=α、β。可以看出，d-q坐标下，系统存在强耦合，若需要精确设计控制器，需要对系统解耦。α-β坐标下，系统在α轴和β轴上相互独立，三相并网逆变器可以等效为两个单相并网逆变器。

2 LCL型并网逆变器在d-q和α-β坐标系下的特性

根据式(2)～式(5)可以得到d-q及α-β坐标下，系统的等效框图如图2及图3所示。图2可等效变换为图4。可以看出，系统存在强耦合，若需要设计控制系统，需要进行解耦控制。从图4可知，若需完全解耦，则应该引入反馈控制[2,3]，如图5所示。显然，若需完全解耦，则需要引入微分项，而实际系统中微分项易引入噪声，尤其是二次微分项对噪声很敏感。并且，从图中可知，耦合项与系统主电路参数有关，因此，要达到完全解耦的控制效果，反馈项对系统参数的精度依赖程度很高，在实际系统中显然很难做到。

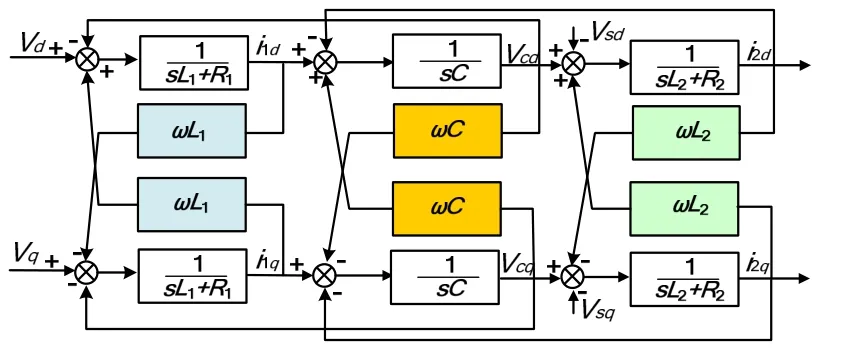
图2 d-q坐标系下系统的控制框图

图3 α-β坐标系下系统的控制框图

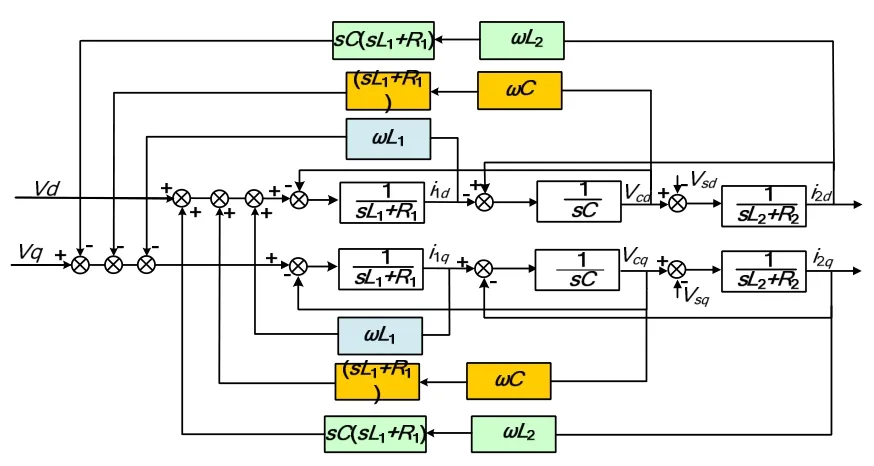
图4 d-q坐标系下系统的等效变换框图

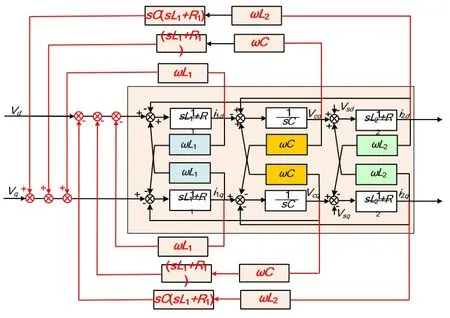
图5 d-q坐标系下系统的完全解耦控制框图

在实际系统中，对于大功率场合，由于L1，L2比较小，因此，在解耦控制中，可以忽略耦合项ωL1，ωL2。在小功率的应用场合，由于C比较小，耦合项ωC可以忽略。当电网电压畸变时，要削弱电网电压对并网电流的影响，需要引入电网电压前馈控制，此时系统若不进行解耦控制，则d轴和q轴的前馈函数存在耦合，若要d轴和q轴的电网电压前馈项相互独立，则需要对系统进行完全解耦。

在d-q坐标系下，系统的控制量为直流量，因此，使用传统的 PI调节器，系统即可实现零稳态误差控制。在α-β坐标系下，系统在α轴和β轴上相互独立，但是系统的控制量仍为交流量，若使用PI调节器，则难以零稳态误差控制。文献[4]及[5]中提到使用比例谐振调节器(PR)，在基频处谐振，产生无穷大增益，以实现并网电流完全无误差跟踪指令电流。PR调节器表达式为：

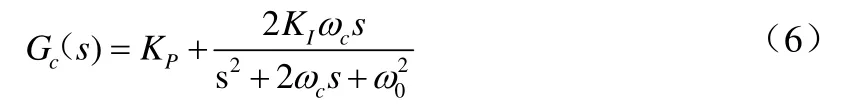
本文分析d-q坐标下的控制选用PI调节器，分析α-β坐标系下的控制，选择改进的PR调节器。

3 d-q和α-β坐标系下三相并网逆变器的控制策略

根据前文分析，α-β坐标下系统选用的控制策略如图6所示。图中，指令电流以d-q轴上的分量给出，其中d轴指令表征并网有功电流分量，q轴指令表征并网电流无功分量，该系统可以实现并网电流的有功与无功独立控制。其中外环调节器选用改进的PR调节器，以实现系统的无静差控制。d-q坐标下，系统简化的控制框图如图7所示，该图中忽略了耦合项。两种坐标系下，系统的主要参数如表1所示。

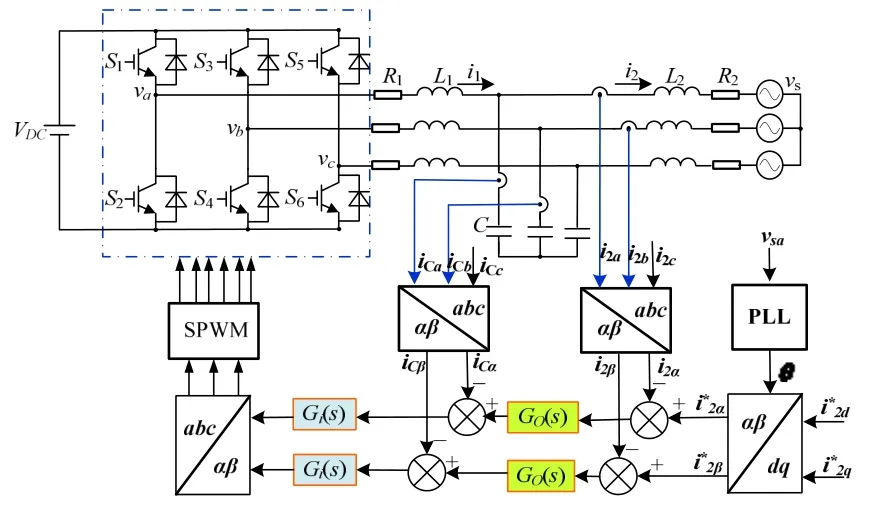
图6 α-β坐标系下系统的控制框图

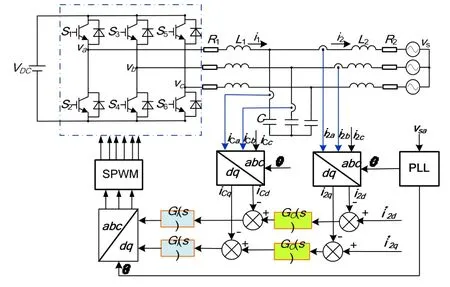
图7 d-q坐标系下系统的控制框图

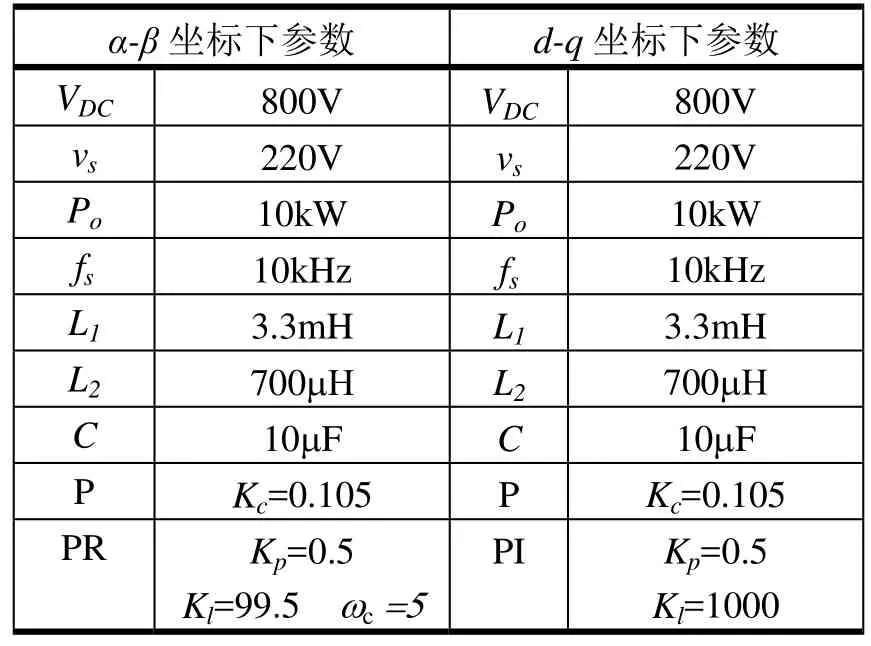
表1 α-β和d-q坐标系下三相并网逆变器参数

4 仿真分析

根据前文分析，基于SABER搭建仿真平台，对两种坐标系下的控制策略进行仿真验证，其中d-q坐标系下，采用简化的解耦控制方法，即忽略了状态反馈解耦项中的一次微分项和二次微分项。

图8给出α-β坐标系下并网电流波形，电流指令为i2*=21.21A，实际电流i2=21.17A，可见采用改进的PR调节器后，系统基本实现无静差控制。图9为系统实现单位功率因数并网的波形(电流波形扩大10倍)；图10为电网频率偏移至49Hz时，并网电流波形，可见使用改进的PR调节器，系统仍能够获得良好的控制效果；图11为系统实现有功与无功独立控制的并网电流波形，其中PF=-0.707。

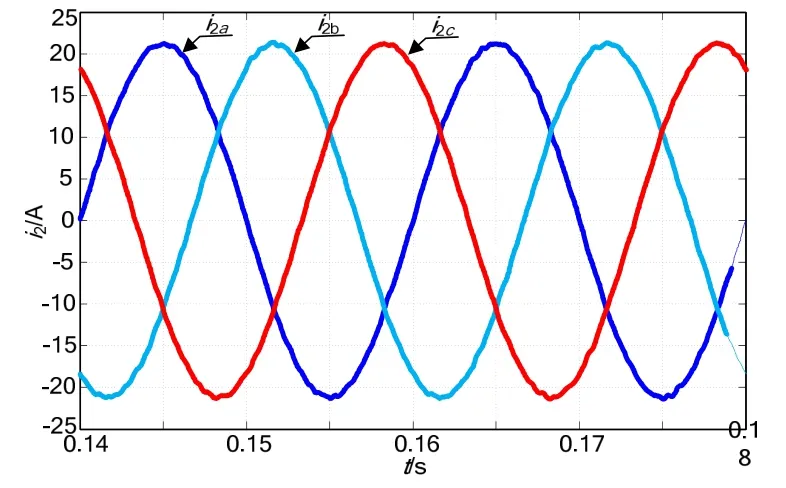
图8 α-β坐标系下并网电流波形(THD=0.6%)

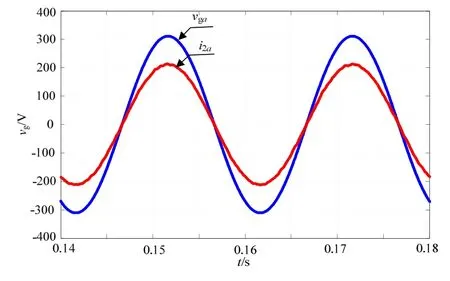
图9 α-β坐标系下电网电压与并网电流波形(PF=1)

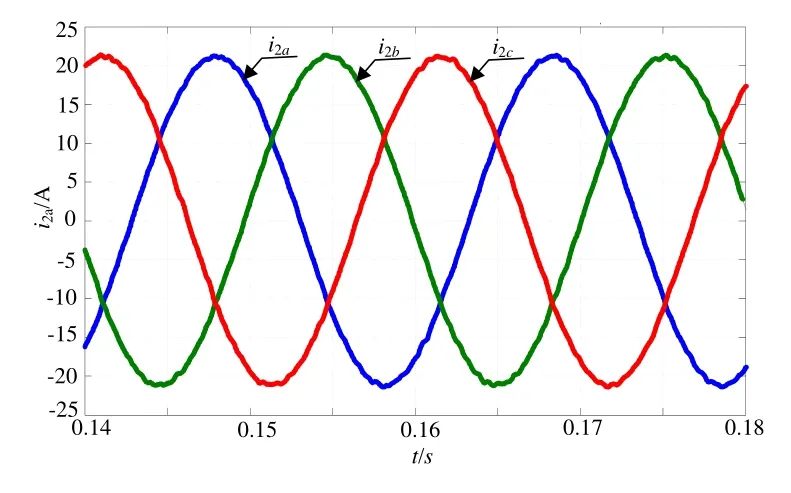
图10 α-β坐标系下电网频率为49Hz并网电流波形

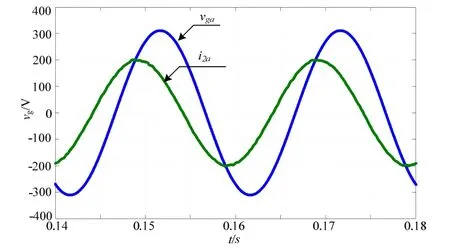
图11 α-β坐标系下电网电压与并网电流波形(PF=-0.707)

图12给出d-q坐标系下并网电流波形，电流指令为i2*=21.21A,实际值为i2=21.21A，即d-q坐标下系下，采用PI调节器即可实现零稳态误差控制。图13给出系统实现单位功率因数并网的波形。

图14为公用电网畸变后的波形，其中含五次谐波有5%，含七次谐波5%，电网总畸变率为5.65%；图15给出电网畸变情况下，α-β坐标系下并网电流波形，图16给出给出电网畸变情况下，d-q坐标系下并网电流波形。

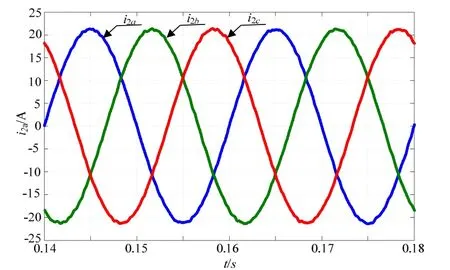
图12 d-q坐标系下并网电流波形(THD=0.62%)

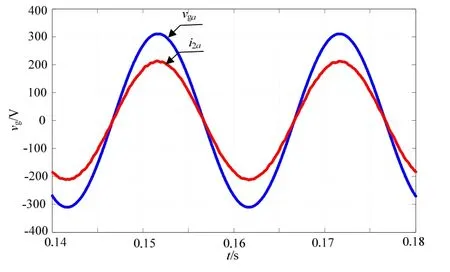
图13 d-q坐标系下电网电压与并网电流波形

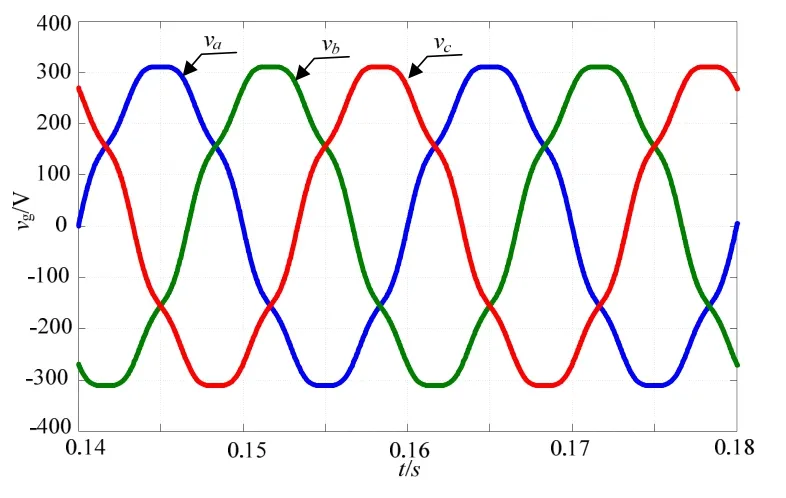
图14 电网电网电压畸变后波形(THD=5.65%)

图15 α-β坐标系下并网电流波形(THD=2.93%)

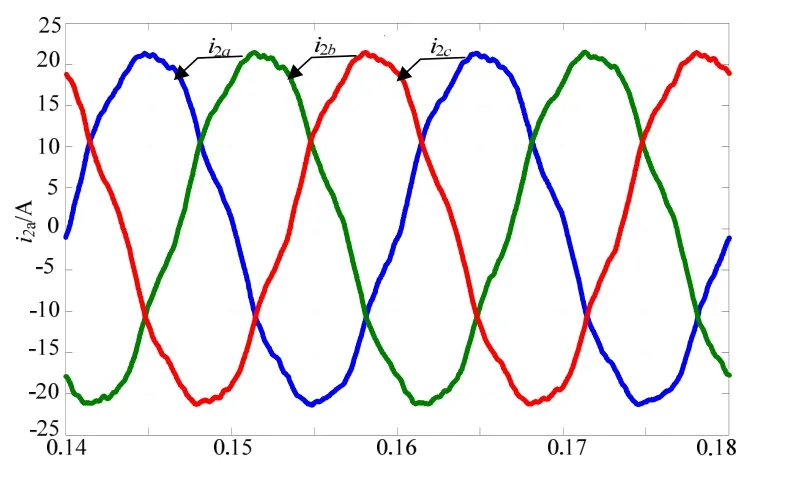
图16 d-q坐标系下并网电流波形(THD=4.43%)

从仿真波形中可以看出，两种坐标下系统的控制策略均能达到良好的效果。其中d-q坐标系下，系统在电网畸变时，并网电流波形THD偏大，一方面是由于所设计的系统输出阻抗在电网5次及7次谐波频率处的输出阻抗不够大，因此对该频段处的谐波衰减不够；另一方面，可能是忽略了耦合项造成的。这方面的原因还有待于进一步分析。

实际上，要从根本上消除电网电压对并网电流的影响，需要引入电网电压前馈控制，关于α-β及d-q坐标下电网电压前馈控制，将在下一步工作中展开。

5 总结

本文针对于分布式发电系统中并网逆变器的控制做了分析。首先在不同坐标系下，建立了LCL型三相并网逆变器的数学模型。接着比较了LCL型三相并网逆变器在d-q和α-β坐标下的控制特性，分析了d-q坐标系下系统的耦合以及解耦方法。最后分析了d-q和α-β坐标下三相并网逆变器的控制策略，基于SABER搭建仿真模型予以验证。

仿真结果表明，本文分析的两种控制策略，均获得良好的控制效果。关于d-q坐标系下，耦合量对系统性能的影响，以及如何削弱电网背景谐波对并网电流的影响，将在下一步工作中深入研究。

[1]赵为.太阳能光伏并网发电的研究[D].合肥:合肥工业大学,2003.

[2]刘飞,殷进军,周彦,段善旭.LCL滤波器的三相光伏逆变器双环控制策略[J].电力电子技术,2008,42(9):29-31.

[3]刘飞.三相光伏发电系统的运行控制策略[D].武汉:华中科技大学,2006.

[4]Twining E,Holmes G.D.Grid current regulation of a three-phase voltage source inverter with an LCL input filter[J].IEEE Transactions on Power Electronics,2003,18(3):888–895.

[5]Teodorescu R,Blaabierg F,Borup U,Liserre M.A new control structure for grid-connected LCL PV inverters with zero steady-state error and selective harmonic compensation[J].Proc.IEEE APEC,2004,1 (1):580-586.

Control Strategy Research on Grid-connected Inverter Used in Distributed Generator System

WU Chun-qiu1,TANG Hui-yan2
(1.Naval Military Reprentative Office in Jiangnan Shipyard (Group) Co.,Ltd.,Shanghai 201913,China; 2.No.711 Research Institute,CSIC,Shanghai 201108,China)

This paper introduces the control strategy of LCL three phase grid-connected inverter.The control characteristics of the three phase grid-connected inverter in different coordinates are analyzed.Finally,one 10kW system is built by SABER and it is verified by simulation.

distributed generator system; LCL; grid-connected inverter

TM464

A

10.16443/j.cnki.31-1420.2015.04.018

吴春秋（1977-），男，工程师。研究方向：船舶自动化。