刀头几何角度对刀型截齿力学特性的影响

宋胜伟， 高修林

(黑龙江科技大学 机械工程学院，哈尔滨 150022)

0 引言

刀型截齿是截割煤岩的刀具，国内外学者对其力学特性进行了大量的研究。陈渠等[1]通过实验研究指出，适当减小截角和主刃宽度有利于改善截割性能。张守柱[2]通过实验方法确定了QJB型扁截齿的几何参数。雷玉勇等[3]认为斜角的存在有利于改善刀齿排屑性能，降低截割阻力和比能耗。郑连宏等[4]研究认为减小前角会增大截割阻力。王洪英等[5]利用自制实验台对镐齿和刀齿分别进行了实验，建立了镐齿的数学模型。耿建平等[6]给出了冲击式采煤机刀齿几何参数了的确定方法。孟波等[7]建立了刀齿冲击破煤力学模型，确定了刀齿的合理几何参数。John P等[8]认为前角为正时，岩石破坏主要是由拉破坏或拉破坏和剪切破坏综合引起的，当前角为负时，主要破坏形式为剪切破坏。学者们从旋转截割的角度对刀齿受力和其自身刀头几何角度之间的关系进行研究相对较少。笔者利用ABAQUS对刀头几何角度与刀齿力学特性的关系进行仿真分析，以期提高刀型截齿的截割效率。

1 有限元模型的建立

仿真模型包括刀型截齿和煤岩两部分，利用ABAQUS和Pro/E建立三维模型，并在ABAQUS中进行相应设置，完成有限元模型的建立。

1.1 煤岩

采用线弹性模型、扩展的线性Drucker－Prager塑性模型、剪切损伤模型、等效塑性应变和耗散能定义煤岩属性[9－10]。煤岩尺寸为130 mm ×100 mm ×200 mm，在截齿运动轨迹方向上弧长为201 mm，分区截面大小为50 mm×55 mm。密度1 500 kg/m3，杨氏模量1 400 MPa，泊松比0.3，煤岩抗压强度28 MPa。煤岩三维模型如图1所示。

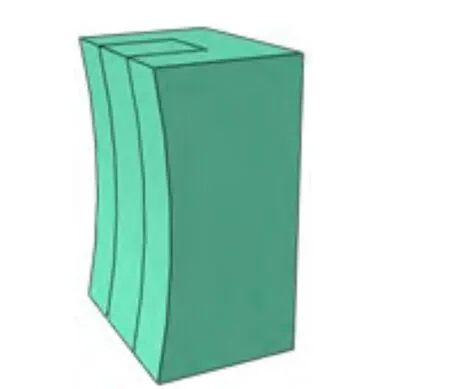
图1 煤岩三维模型Fig.1 Three-dimensional model of coal rock

1.2 刀型截齿

1.2.1 刀型截齿刀头角度

刀齿刀头角度及运动方向如图2所示。α为前角，β为后角，δ为截角，θ为两侧刀面在垂直刀面凸脊方向上的夹角，简称为侧刀面夹角。l1为侧刀面在平行于截割方向上的投影长度，l2为侧刀面在垂直于凸脊方向的投影长度，b为截齿宽度。斜角和侧刀面夹角的关系推导如式(1)～(4)所示。

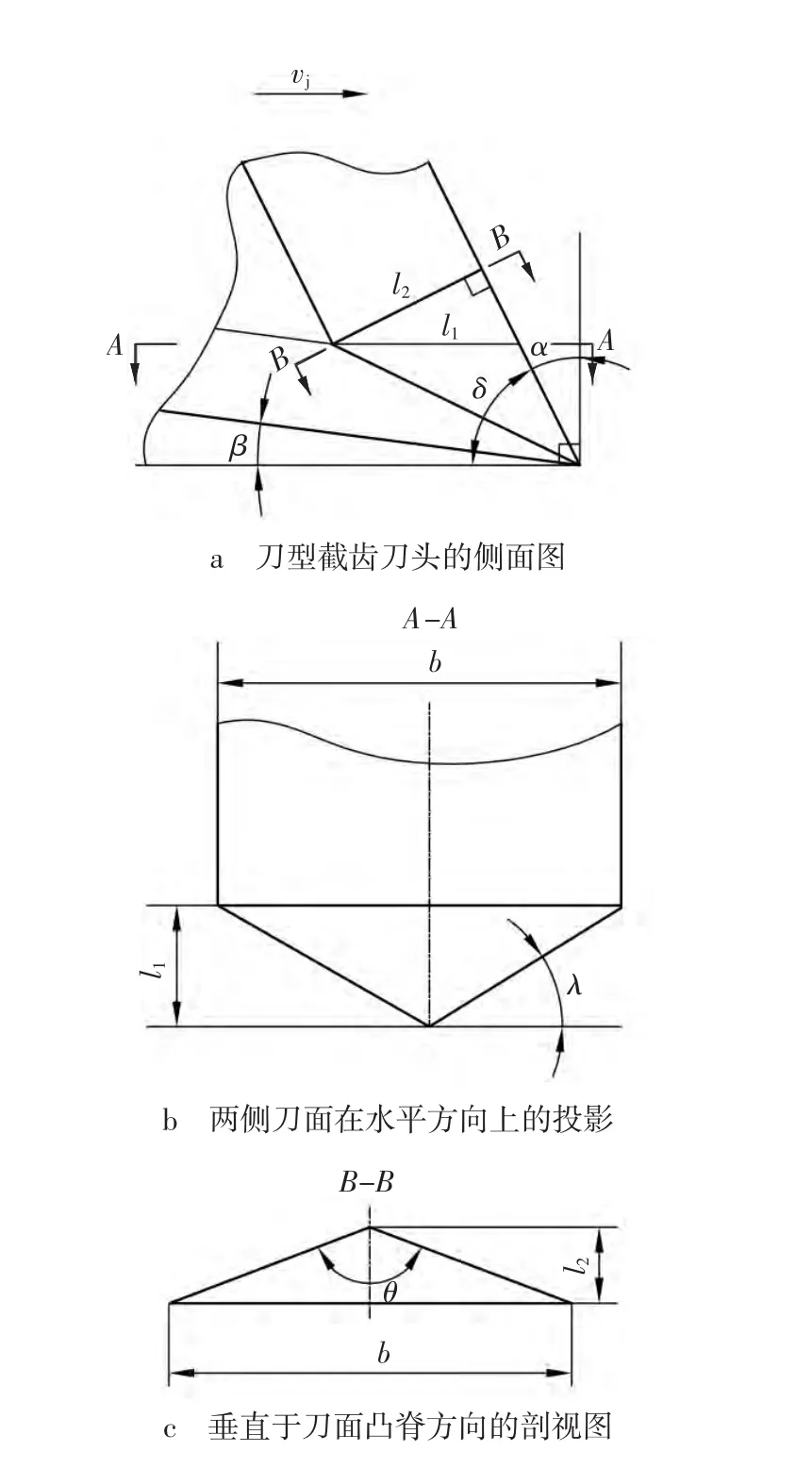
图2 刀齿刀头角度Fig.2 Cutting blade angle of flat pick

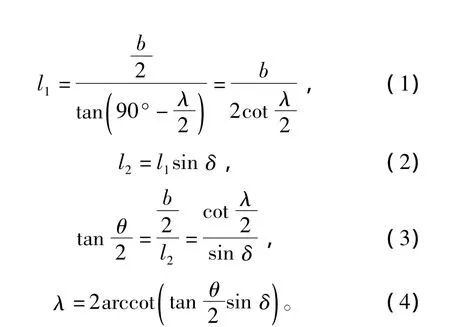
由式(4)可知，斜角λ不仅和侧刀面夹角θ有关，还与截角δ有关。当δ在0～90°范围内时，λ随着θ增大而减小，随θ减小而增大。

1.2.2 刀型截齿

在Pro/E中建立刀齿三维模型，将其导入ABAQUS的Part模块中。在Property模块中分别定义齿体和硬质合金刀片的材料属性。齿体材料为42CrMo，密度 7 800 kg/m3，杨氏模量 20 GPa，泊松比0.3。硬质合金刀片材料为YG11C，密度14 600 kg/m3，杨氏模量600 GPa，泊松比0.22。

1.3 模型参数

在Assembly模块中，设置刀齿为径向安装。在Step模块设置时间为0.07 s。在Interaction模块中进行相应的相互作用属性和相互作用设置。在Load模块中设置煤岩和刀齿的边界条件。滚筒转速35 r/min，牵引速度4 m/min。由于模拟的是一个完整切削过程的一部分，故初始时的切削厚度不为零，设定此厚度为初始切削厚度。切削厚度由初始切削厚度和切削厚度增量组成。切削厚度增量为切削厚度在牵引方向上的变化量，最大切削厚度增量即仿真时间与牵引速度的乘积。初始切削厚度为15 mm。根据计算可知，最大切削厚度增量为4.7 mm，故最大切削厚度为19.7 mm。在Mesh模块中对刀齿和煤岩进行网格划分，装配模型如图3所示。

图3 刀齿截割煤岩装配模型Fig.3 Assembly model of flat pick cutting coal rock

2 不同刀头角度的力学性能

2.1 斜角

以斜角为变量，建立四种刀齿模型。侧刀面夹角分别为 110°、120°、130°和 140°，对应斜角分别为73.4°、63.1°、52.8°和 42.3°。前角 20°，后角 10°。刀齿应力分布云图如图4所示，三向载荷截割力Fj、侧向力Fc和牵引力Fq如图5所示。

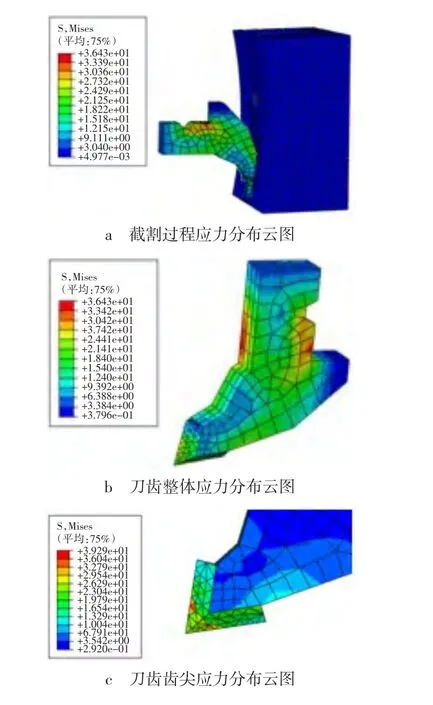
图4 刀齿应力云图Fig.4 Stress nephogram of flat pick

由图4a、b可知，刀齿齿体与齿座接触的部分受到较大的应力作用。一方面是因为刀齿采用径向安装形式，伸出长度大，更易受到大的弯矩作用，另一方面则是因为截齿安装在齿座中的部分尺寸较小。由图4c可知，靠近截齿齿尖以及前后刀面的凸脊部分应力最大，这是因为齿尖和凸脊最先与煤岩发生接触，并在截割过程中受到密实核的挤压作用。

由图5可知，刀齿三向载荷都为无规则波动。截割阻力波动程度最为剧烈，牵引阻力的波动程度较小，这是煤岩突然崩落造成的。侧向阻力在y轴零值附近上下正负波动，这是截齿侧刀面受煤岩挤压及煤岩崩落的不同步造成的。

以全部峰值的平均值反映刀齿峰值变化，简称峰值均值，以整体数据的平均值反映刀齿平均受力，以标准差s衡量载荷波动情况。由图5可以很明显地看出，侧向阻力的特点，故不再对侧向阻力做更深入的讨论，而是重点分析截割阻力、牵引阻力和各影响因素之间的关系。对仿真数据提取、处理后，绘制描述截割阻力和牵引阻力的三个评价指标与斜角之间关系的散点图并添加拟合曲线，分别如图6、图7所示，其中1为截割阻力峰值均值拟合曲线，2为截割阻力均值拟合曲线，3为牵引阻力峰值均值拟合曲线，4为牵引阻力均值拟合曲线。

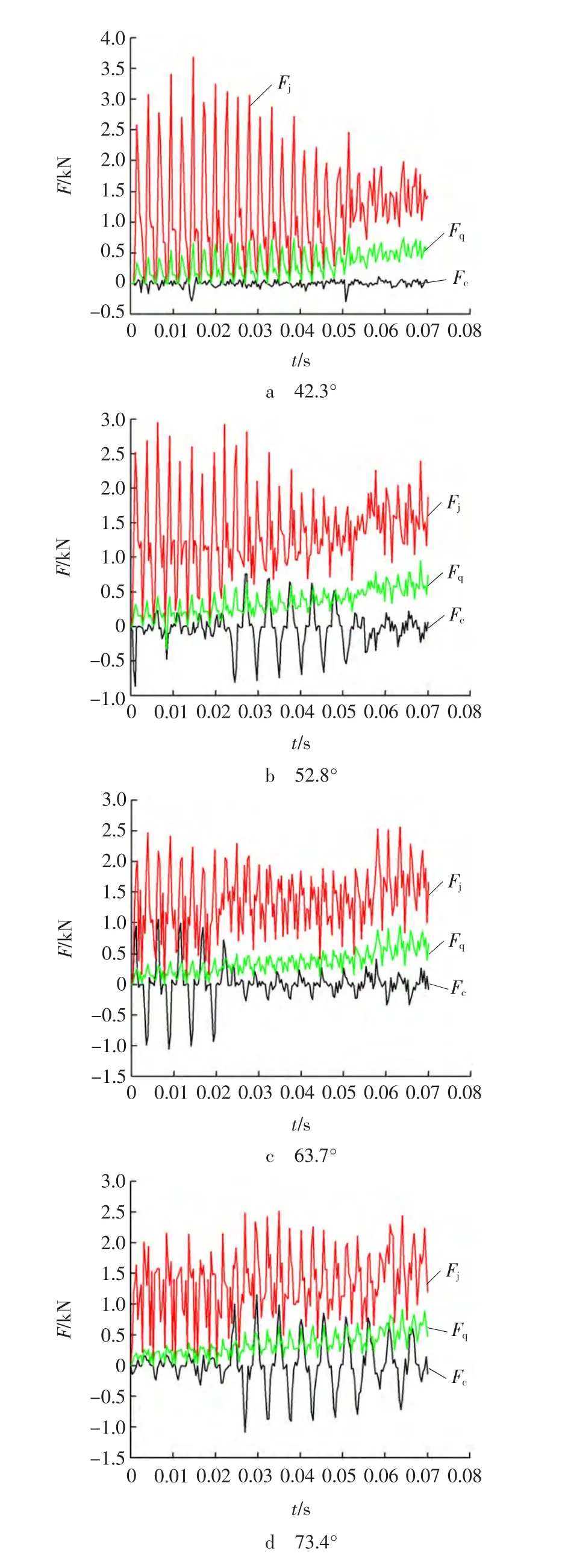
图5 不同斜角时刀齿三向载荷曲线Fig.5 Curves of three directional load on flat pick with diverse bevel angle

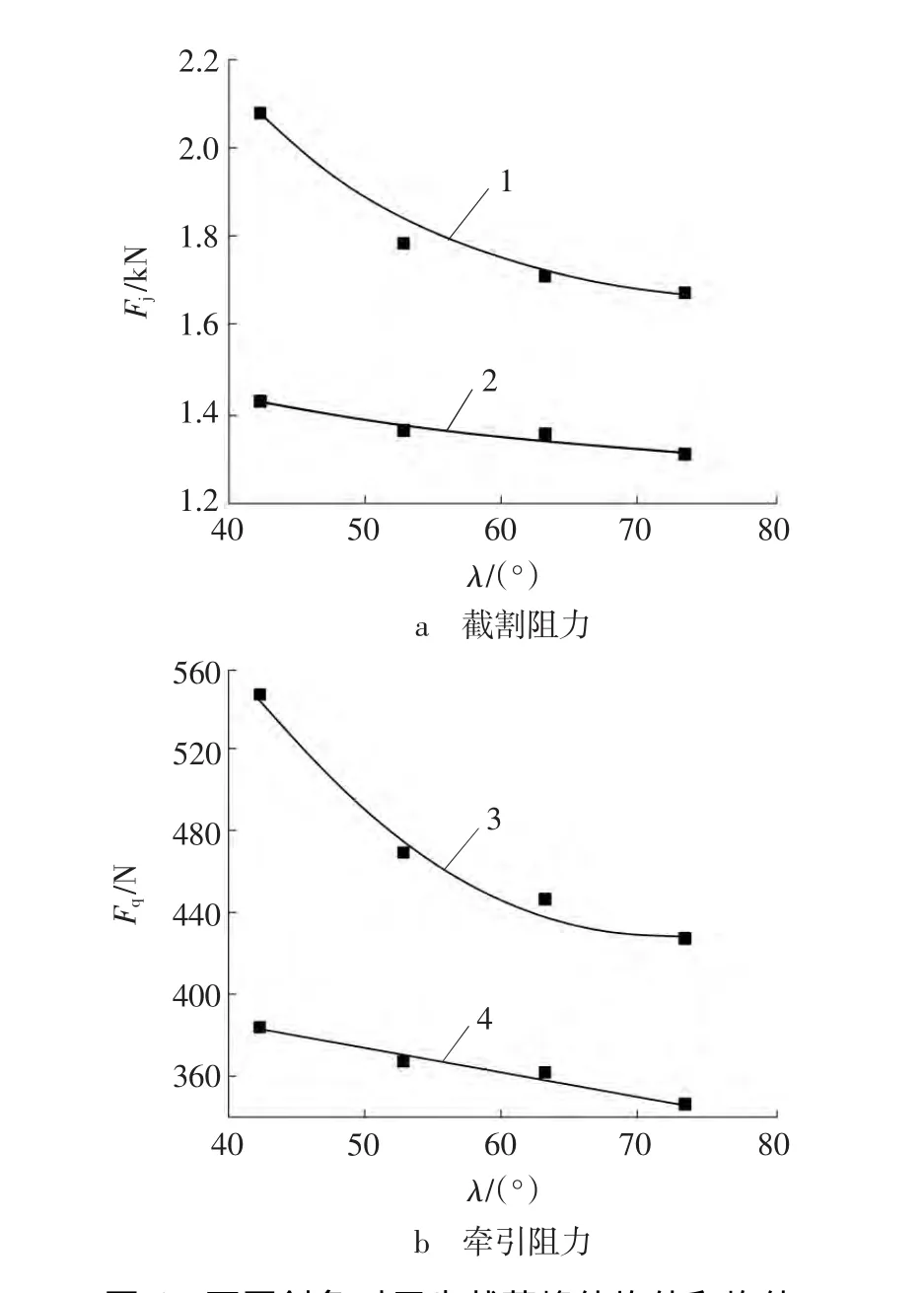
图6 不同斜角时刀齿载荷峰值均值和均值Fig.6 Mean value and average of peak value on force of flat pick with diverse bevel angle

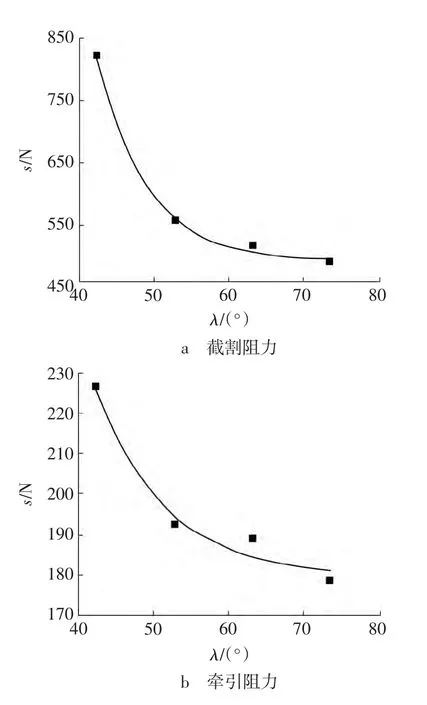
图7 不同斜角时刀齿载荷标准差Fig.7 Standard deviation of force on flat pick with diverse bevel angle

由图6a可知，随着斜角的增大，截割阻力峰值均值及均值逐渐减小。这是因为随着斜角的增大，刀齿的屋脊状特征更加明显，截齿和煤岩在截割方向上的接触面积变小。由图6b可知，牵引阻力峰值均值及均值同样随着斜角的增大而减小。这是因为斜角增大有利于切屑的排出，致使密实核不能完全发育。

由图7a和b可知，随着斜角的增大，截割阻力标准差和牵引阻力标准差都逐渐减小。这是因为增大斜角可以加速切屑排出，煤岩对齿面作用力的波动减小，说明斜角的增大有利于降低截割阻力和牵引阻力的波动程度。

2.2 前角

以前角为变量，建立四种刀齿模型。前角分别为 14°、16°、18°、20°，后角 10°，斜角 73.4°。提取数据并处理，分别如图8、图9所示，其中1为截割阻力峰值均值拟合曲线，2为截割阻力均值拟合曲线，3为牵引阻力峰值均值拟合曲线，4为牵引阻力均值拟合曲线。

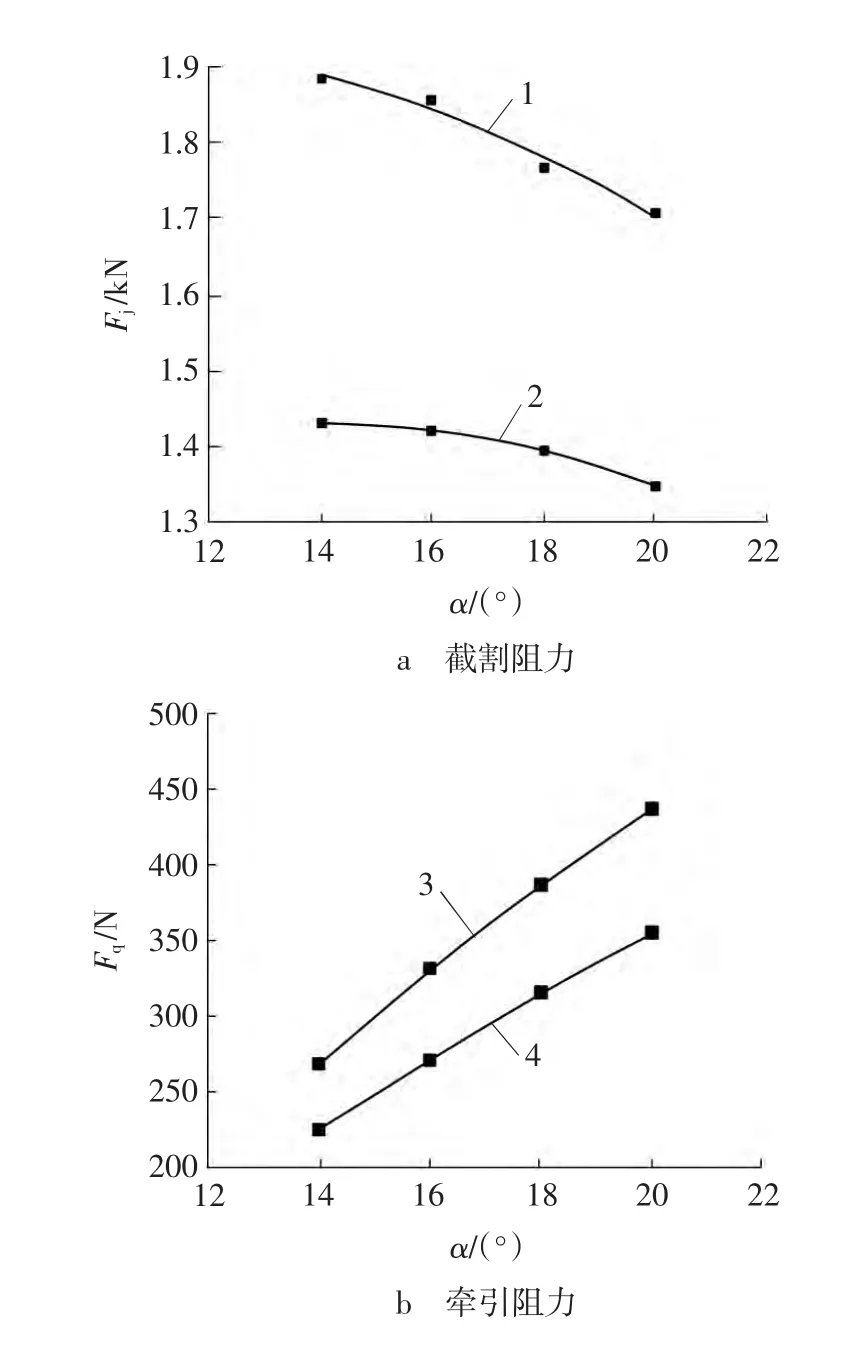
图8 不同前角时刀齿载荷峰值均值和均值Fig.8 Mean value and average of peak value on force of flat pick with diverse rank angle

由图8a可知，随着前角的增大，截割阻力峰值均值及均值都逐渐减小。这是因为随着前角增大，煤岩垂直作用于刀齿前刀面方向的力不断减少，并且破碎的煤岩可以加速排出。由图8b可知，牵引阻力峰值均值及均值都随着前角的增大而增大。这是因为在截齿截割煤岩的过程中，破碎煤岩对后刀面有挤压作用并且无法排出，从而造成牵引阻力的增大。

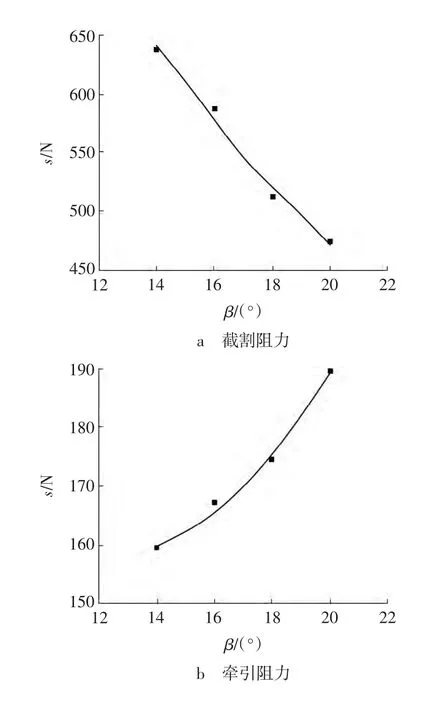
图9 不同前角时刀齿载荷标准差Fig.9 Standard deviation of force on flat pick with diverse rank angle

由图9a可知，随着前角的增大，截割阻力标准差呈现下降趋势，截割阻力数据离散程度降低。由图9b可知，牵引阻力标准差随着前角的增大而增大，牵引阻力数据离散程度增大。这是因为前角增大及后角固定，导致截齿刀头强度减弱，所以牵引阻力更容易产生波动。而前刀面因为有斜角的存在，可以相互抵消一部分的作用力，并且可以排出煤粉，故不会因前角增大造成截割阻力波动程度增大。

2.3 后角

以后角为变量，建立五种刀齿模型。前角20°，后角分别为 6°、8°、10°、12°和 14°，斜角 73.4°。提取数据并处理，分别如图10、图11所示，其中1为截割阻力峰值均值拟合曲线，2为截割阻力均值拟合曲线，3为牵引阻力峰值均值拟合曲线，4为牵引阻力均值拟合曲线。

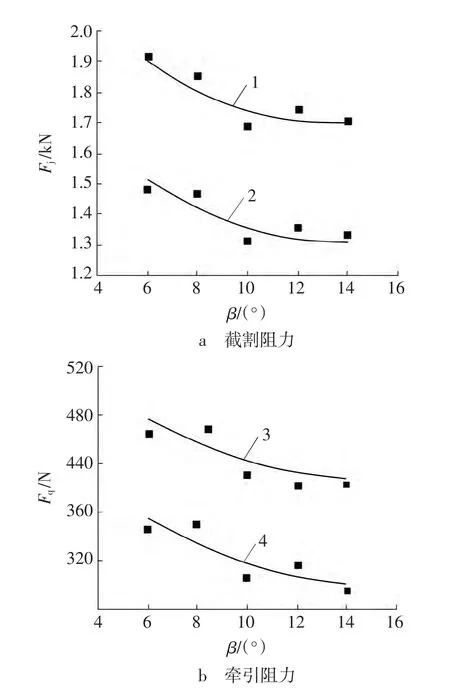
图10 不同后角时刀齿载荷峰值均值及均值Fig.10 Mean value and average of peak value on force of flat pick with diverse relief angle

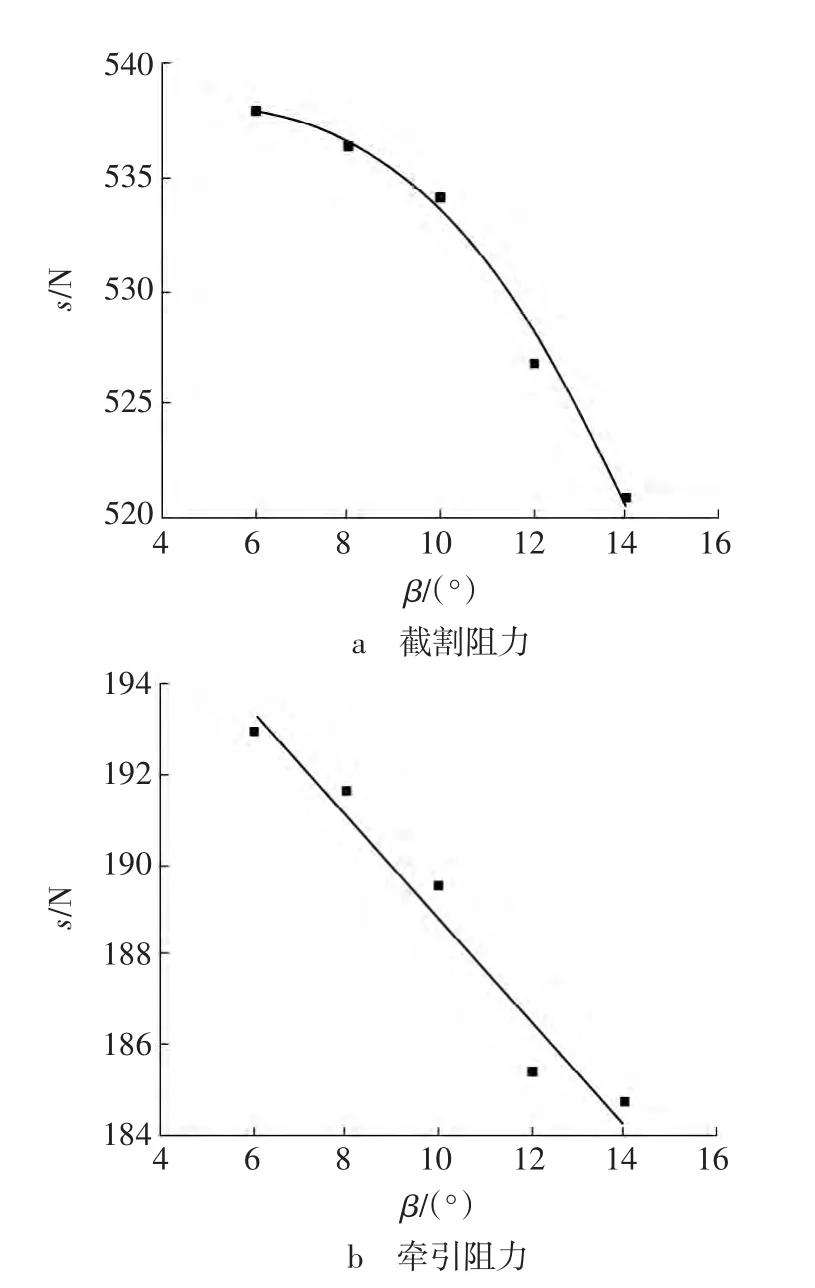
图11 不同后角时刀齿载荷标准差Fig.11 Standard deviation of force on flat pick with diverse relief angle

由图10a可知，随着后角增大，截割阻力峰值均值及其均值均呈现下降趋势。由图10中b图可知，牵引阻力峰值均值及均值同样随着后角的增大而减小。这是因为当后角为正，且逐渐增大时，可以避免截齿和煤岩直接发生接触，从而降低截割阻力和牵引阻力。

由图11可知，随着后角增大，截割阻力标准差和牵引阻力标准差逐渐减小。说明后角越大，截割阻力和牵引阻力的数据波动程度越小。这是因为后角增大与截齿后刀面接触的煤岩破碎程度减小，对后刀面的作用力也减小。

3 截割阻力均值与后角的回归方程

回归分析是处理两个或两个以上变量之间定量关系的一种最常用的统计方法，用此方法可以发现隐含在随机数据内部的统计规律[10]。回归分析有多种类型，根据研究内容，选用一元非线性回归分析方法建立截割阻力均值和后角间的回归方程。

3.1 回归方程的建立

根据前面分析可知，截割阻力均值和后角之间接近二次函数关系。故假设回归方程为:

β——刀齿后角，(°);

a，b1，b2——回归系数。

令x1=β，x2=β2，y=¯P，则回归方程可写成y=a+b1x1+b2x2，即将一元非线性问题转化为多元线性问题分析。按照多元线性回归分析要求，对截割阻力均值和后角数据进行处理，得到正规方程组:

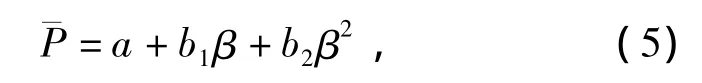
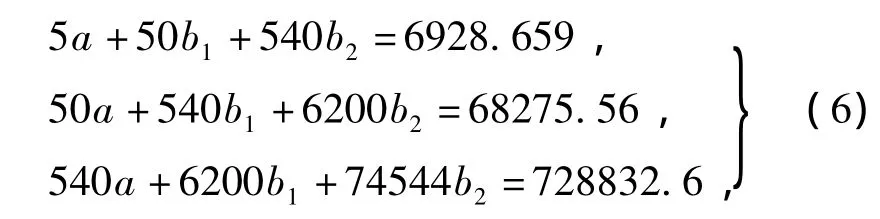
解得 a=1949.82，b1= －92.96，b2=3.38，所以回归方程为

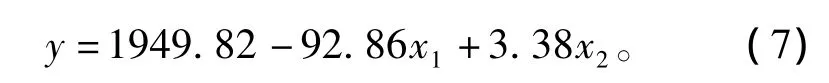
3.2 回归方程显著性检验

采用相关系数检验法进行显著性检验。总离差平方和SST=29 378.26，偏差平方和SSR=28 120.46，则复相关系数R为

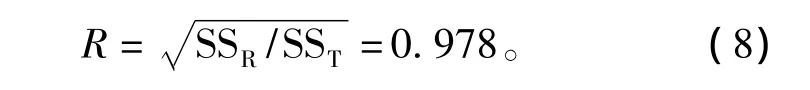
给定显著性水平 α=0.05，n=5，自变量个数m=2，查资料得Rmin=0.975。可知R＞Rmin，所以所建立的多元非线性回归方程与仿真数据拟合得很好。拟合曲线如图10中曲线2所示。因此所求的二次多项式为:

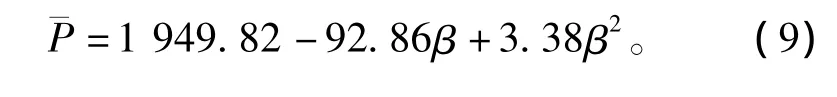
4 结论

(1)增大斜角或后角，可以减小截割阻力和牵引阻力的峰值以及平均值，同时也可以降低截割阻力和牵引阻力的波动程度。

(2)增大前角可以减少截割阻力的峰值均值、平均值，降低波动程度，但是会使牵引阻力的峰值均值、平均值，波动程度增加。

(3)建立了截割阻力均值和截齿后角之间的回归方程，经过显著性分析，验证了回归方程能够很好地反映两者之间的关系。

[1]陈 渠，高天林.楔形截齿最佳截槽间距的研究[J].重庆大学学报，1989，12(4):100－105.

[2]张守柱.采煤机高效QJB型扁截齿[J].煤矿机电，1998(1):40－54.

[3]雷玉勇，李晓红，杨 林，等.煤岩切割刀具几何参数的理论分析[J].煤矿机械，1999(6):20－22.

[4]郑连宏，李文华.采煤机刀齿前角的实验研究[J].辽宁工程技术大学学报:自然科学版，2002，21(1):105－107.

[5]王洪英，刘春生，王金波.采煤机镐形齿与刀形齿截割力实验分析[J].煤矿机械，2002(6):29－31.

[6]耿建平，田取珍，杨双锁.冲击式采煤机刀齿几何参数的优化[J].太原理工大学学报，2003，34(4):393－394.

[7]孟 波，田取珍，徐彦明，等.冲击式采煤机刀齿受力分析及其几何参数的确定[J].山西煤炭，2001，21(4):9－11.

[8]JOHN P，LOUI U，RAO M.Numerical studies on chip formation in drag-pick cutting of rocks[J].Geotechnical and Geological Engineering，2012，30(1):145 －161.

[9]陈明祥.弹塑性力学[M].北京:科学出版社，2007:61－78.

[10]宋 杨.镐型截齿截割煤岩力学特性的数值模拟[D].哈尔滨:黑龙江科技大学，2013:30－35.

[11]李云雁，胡传荣.实验设计与数据处理[M].北京:化学工业出版社，2005:44－87.