基于广义形态学的高光谱图像解混算法

赵　岩,　张春晶,　王东辉

(1.黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022; 2.黑龙江科技大学 电子与信息工程学院,哈尔滨 150022; 3.哈尔滨工程大学 信息与通信工程学院, 哈尔滨 150001)



基于广义形态学的高光谱图像解混算法

赵岩1,张春晶2,王东辉3

(1.黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022; 2.黑龙江科技大学 电子与信息工程学院,哈尔滨 150022; 3.哈尔滨工程大学 信息与通信工程学院, 哈尔滨 150001)

综合利用像元的光谱和空间信息,提出一种基于广义形态学的混合像元分解算法。引入基准像元,避免形态学算子在像元排序规则和替换准则上存在的局限性。针对图像中不同类别交界处存在的交叉替换现象,广义开-闭算子采用修正能量函数作为距离测度进行计算。端元提取之后利用全约束最小二乘法进行丰度反演。利用矿物光谱的模拟数据和真实数据进行实验,结果表明,该算法无需先验信息便可自动进行混合像元分解,分解精度较高。

高光谱混合像元分解; 广义形态学; 修正能量函数

地球表面很少由均一物质组成,当具有不同波谱属性的物质出现在同一个像元内时,就会出现混合现象,即混合像元(Mixed Pixel)[1-4]。高光谱图像混合像元分解技术可应用于矿产资源勘探等领域。在线性混合模型[5]进行光谱解混操作之前,需要进行光谱端元提取,为光谱解混获取必要的先验知识。光谱端元的选择应当具有代表性,成为图像内大多数像元的类别成分集合[6]。端元波谱作为混合像元分解过程中的参考波谱,影响混合像元分解结果的精度[7]。常用的获取端元波谱的方法有纯净像元指数(Pixel Purity Index, PPI)、N-FINDR算法、顶点成分分析(Vector Component Analysis, VCA)、迭代误差分析(Iterative Error Analysis, IEA)、独立成分分析(Independent Component Analysis, ICA)等。这些方法只是考虑光谱信息,而忽略了像素间的空间相关性[8]。自动形态学端元提取(Automated Morphological Endmember Extraction, AMEE)[9],在高光谱图像处理中引入反映像素间空间相关性信息的形态学算子。AMEE算法膨胀运算应用到图像中不同地物类别的边界处时,出现交叉替换现象。笔者引入正则化的修正能量函数作为距离测度,同时给出关键参量——基准像元的计算方法,通过计算广义形态开-闭算子进行端元提取,之后进行全约束最小二乘法[10]丰度反演,名为广义形态学端元提取-全约束最小二乘算法(Generalized Morphological Endmember Extraction-Fully Constrainded Least Squares, GMEE-FCLS)。

1　广义形态学算子

1.1线性光谱混合模型

线性光谱混合模型(Linear Spectral Mixture Model,LSMM)计算简单,应用广泛,是混合像元分解的常用方法。设X为像元光谱向量,S=[s1,s2,…,sN]为端元光谱矩阵,A=[a1,a2,…,aN]T是N维向量,其各分量元素为端元丰度,N为随机噪声。线性光谱混合模型为:

X=SA+N,

(1)

ai≥0,

(2)

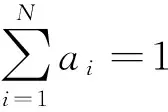
(3)

1.2能量函数

能量函数(Energy Function)为相邻像元的能量测度[11],它包含图像的空间信息。考虑N维光谱向量si=[si1,si2,…,siN]T,sj=[sj1,sj2,…,sjN]T,则si和sj的EF为

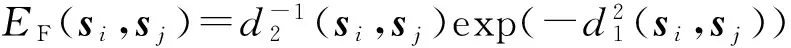
(4)

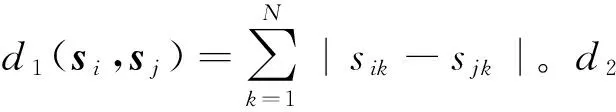
1.3修正能量函数

常用的表征光谱间相似性的距离测度有光谱角(Spectral Angle Distance, SAD)、欧式距离(Euclidean Minimum Distance, EMD)、光谱信息散度(Spectral Information Divergence, SID)、马氏距离(Mahalanobis Distance, MD)等。文中引入修正能量函数(Modified Energy Function, MEF)计算该距离。将EF中的欧式距离d2替换为加入正则化项的马氏距离d3。将正则化项加入协方差矩阵中,可以提高求取协方差矩阵的逆阵的稳定性,使其适用于稍小的样本[12]。马氏距离可以排除光谱波段之间的相关性的干扰。修正能量函数(ECF)为

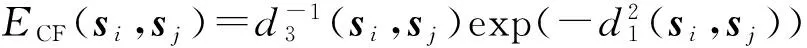
(5)

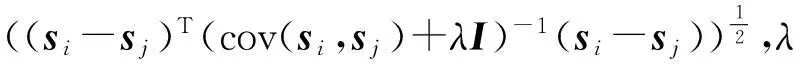
结构元素的尺寸和结构形状影响形态学图像空间信息的提取[13]。广义形态学算子采用两个不同尺寸结构元素,输出统计偏倚小于经典形态学算子[14],端元提取性能得到改善。基于导出序的广义形态学算子将光谱向量作为整体处理[15],广义开-闭算子(GOC)和广义闭-开算子(GCO)[16]为

GOC(f(x,y))=(f∘B1·B2)(x,y),

(6)

GCO(f(x,y))=(f·B1∘B2)(x,y),

(7)

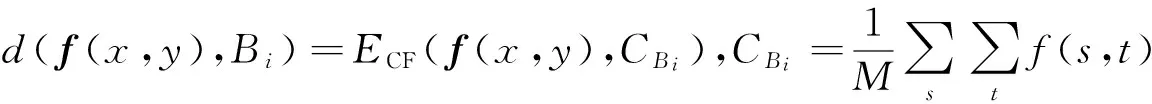
通常情况下,纯像元的GOC值最大,GCO值约为零,而混合像元的GCO值最大,GOC值约为零。

1.5基准像元

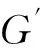
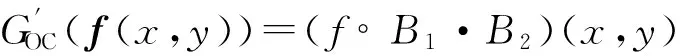
(8)

其中,度量算子d(f(x,y),Bi)=ECF(f(x,y),e(j,k)),e(j,k)为基准像元,

e(j,k)=argmax(GCO(f(x,y))。

(9)

2　端元提取算法与丰度反演

2.1基于广义形态学算子的端元提取算法

基于广义形态学算子的端元提取步骤:

步骤1将利用虚拟维度法(Virtual Dimensionality, VD)[18]估计出的端元数作为算法的终止条件。当已提取的端元数达到VD估计的端元数时,结束运算。

步骤2设定结构元素B1、B2的空间尺寸。

步骤3遍历整幅图像计算基准像元e(j,k)。

步骤7若未满足步骤1的终止条件,重复步骤4。

2.2全约束最小二乘法丰度反演

采用满足“非负”和“和为1”的全约束最小二乘法进行丰度反演。

(10)

将式(10)代入“非负”约束最小二乘法[8](Nonegatively Constrainded Least Squares, NCLS)得到全约束最小二乘法的丰度解。

3　实验分析

3.1性能指标

解混精度评价采用光谱角距离(dSAD)和均方根误差(Re)这两个常用的指标。

对于第i个端元,dSAD定义为

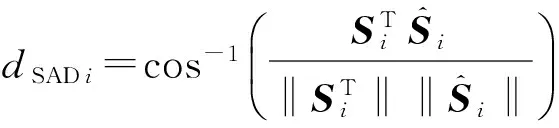
(11)

Re定义为

(12)

3.2模拟数据实验

模拟实验数据由USGS矿物光谱库中选取出五种线性独立的端元光谱,按照Dirichlet分布进行混合。端元丰度之和进行归一化处理,加入不同强度的白噪声,波段数为50,图像大小为256×256像元。

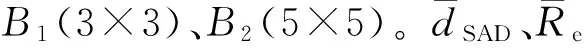
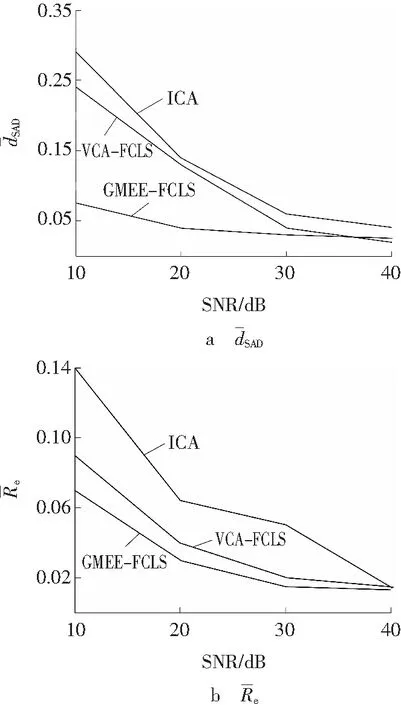
图1　不同噪声强度时不同算法性能的比较

3.3真实数据实验

真实图像采用美国内华达州Cuprite地区的AVIRIS(AirborneVisible/InfraredImagingSpectrometer)高光谱数据(400×350像元,波长范围1.99～2.48μm,成像于1995年),共计172～221波段间的50个波段数据,图2为第196波段。实验中去掉大气吸收的221波段,实际采用49个波段。

图2　内华达州Cuprite地区的AVIRIS图像

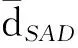
表1　Cuprite地区数据的光谱角距离比较

图3　基于GMEE-FCLS算法的解混结果

4　结束语

基于广义形态学算子的高光谱混合像元分解方法,从结构元素中像元的排序规则和替换准则入手,引入基准像元,并以修正能量函数为距离测度。该GMEE-FCLS算法结合光谱和空间信息,考虑光谱波段的相关性。矿物光谱的模拟和真实数据实验分析表明，文中提出的方法能够提高混合像元分解的精度。

[1]GREER J B. Sparse demixing of hyperspectral images[J]. IEEE Transactions on Image Processing, 2012, 21(1): 219-228.

[2]YOKOYA N, CHANUSSOT J, IWASAKI A. Nonlinear unmixing of hyperspectral data using semi-nonnegative matrix factorization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014 52(2): 1430-1437.

[3]赵春晖, 崔士玲, 刘务. 基于分层的多端元光谱解混算法[J]. 光电子·激光, 2014, 25(9): 1830-1836.

[4]杨可明, 王林伟, 刘士文, 等. 压缩感知和万有引力模型相结合的高光谱混合像元分解[J]. 测绘学报, 2014, 43(10): 1068-1074.

[5]NEVILLE R A, STAENZ K, SZEREDI T, et al. Automatic endmember extraction from hyperspectral data for mineral exploration[C]//Fourth International Airborne Remote Sensing Conference and Exhibition. Canada： [s.n.], 1999: 21-24.

[6]王立国, 赵春晖. 高光谱图像处理技术[M]. 北京: 国防工业出版社, 2013: 11.

[7]邓书斌. ENVI遥感图像处理方法[M]. 北京: 科学出版社, 2010: 334.

[8]JI R R, GAO Y, HONG R C, et al. Spectral-spatial constraint hyperspectral image classification[J]. IEEE Transactions Geoscience and Remote Sensing, 2014, 52(3): 1811-1824.

[9]杜培军, 谭琨, 夏俊士. 高光谱遥感影像分类与支持向量机应用研究[M]. 北京: 科学出版社, 2012.

[10]张兵, 高连如. 高光谱图像分类与目标识别[M]. 北京: 科学出版社, 2011: 147-148.

[11]孙显, 付琨, 王宏琦. 高分辨率遥感图形理解[M]. 北京: 科学出版社, 2011: 145.

[12]NASRABADI N M. Regularization for spectral matched filter and RX anomaly detector[C]//SPIE, Defense and Security Symposium. [S.l.]: International Society for Optics and Photonics, 2008, 6966: 1-12.

[13]刘生, 王晓宇, 邱新法. 一种高分辨率遥感影像的数学形态学滤波算法[J]. 气象与减灾研究, 2008, 31(4): 48-51.

[14]段汕. 形态学及其在遥感影像处理中的应用研究[D]. 武汉: 武汉大学, 2004: 115-124.

[15]PLAZA A, MARTINEZ P, PLAZA J, et al. Dimensionality reduction and classification of hyperspectral image data using sequences of extended morphological transformations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(3): 466-479.

[16]赵春晖. 数字形态滤波器理论及其算法研究[D]. 哈尔滨: 哈尔滨工业大学, 1998: 59.

[17]王瀛, 梁楠, 郭雷. 一种基于修正扩展形态学算子的高光谱遥感图像端元提取算法[J]. 光子学报, 2012, 41(6): 672-677.

[18]CHANG CHEIN-I, DU QIAN. Estimation of number of spectrally distinct signal sources in hyperspectral imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(3): 608-619.

(编辑徐岩)

Generalized morphology-based hyperspectral image unmixing algorithm

ZHAOYan1,ZHANGChunjing2,WANGDonghui3

(1.School of Electric & Control Engineering, Heilongjiang University of Science & Technology, Harbin 150022, China; 2.School of Electronic & Information Engineering, Heilongjiang University of Science & Technology, Harbin 150022, China; 3.College of Information & Communication Engineering, Harbin Engineering University, Harbin 150001, China)

This paper introduces an unmixing algorithm based on generalized morphology, thanks to comprehensive utilization of pixel spectral and spatial information. The algorithm study consists of introducing reference pixel and avoiding morphological operator which suffers from limitations in the pixel arrangement rule and replacement criteria; calculating the generalized open-closing operator using the modified energy function as a distance measure in response to cross substitution occurring in different types of junction in the image; and performing abundance inversion using fully constrainded least squares, after the endmember extraction. The experiment using simulated data and real data of mineral spectrum shows that proposed algorithm has a demonstrated ability to automatically decompose mixed pixel without prior information and exhibits a higher decomposition precision.

hyperspectral unmixing; generalized morphology; modified energy function

2015-03-23

黑龙江省教育厅科学技术研究面上项目(12541734)

赵岩(1976-),女,黑龙江省齐齐哈尔人,讲师,硕士,研究方向:图像处理、智能控制,E-mail:zh-ao-yan@sina.com。

10.3969/j.issn.2095-7262.2015.03.023

TN911.73

2095-7262(2015)03-0343-05

A