基于零阶算法的轨道吊结构优化设计
2015-10-15尹征南
项 青,尹征南,秦 昊
(1.上海大学上海市应用数学和力学研究所,上海 200072;2.上海市特种设备监督检验技术研究院,上海 200333)
基于零阶算法的轨道吊结构优化设计
项青1,尹征南1,秦昊2
(1.上海大学上海市应用数学和力学研究所,上海 200072;2.上海市特种设备监督检验技术研究院,上海 200333)
工程机械轨道吊结构的超差使用,使得材料利用率较低,造成经济成本的浪费.从轨道吊仓主梁结构的力学分析出发,将主梁重量的优化问题转化成力学约束条件下结构设计参数最优值的求解问题.将主梁翼缘板、腹板的几何尺寸作为输入参数,以结构强度、刚度、稳定性作为响应参数,建立了基于零阶算法的数学优化模型,通过有限元数值计算求得主梁的优化设计结果.计算结果表明,采用新的设计方法可以减轻主梁的重量,提高材料的使用效率.
零阶算法;轨道吊结构;优化设计
工程机械中的轨道吊是起重运输设备之一,主要用于钢铁、冶金、建材等行业的大型加工企业.轨道吊对于企业的安全生产具有非常重要的作用.在传统工业设计中,轨道吊结构常采用较大的安全系数,这就使得设备制造材料的利用率较低,造成不必要的材料浪费.箱形主梁是轨道吊的主要结构之一,占轨道吊结构质量的60%以上.因此,对轨道吊的主梁结构进行优化设计,可以在保证设备运行安全可靠的同时减轻箱形主梁的质量,从而减轻轨道吊结构的质量,提高经济效率.由于工况复杂、结构本身的几何特征以及变形的非线性特性,通常采用强度和刚度的被动校核进行安全验证[1-2].结构优化设计是通过力学分析将结构的被动安全校核转变为主动设计结构方案和初选构件的截面尺寸,并从各种可能的设计中寻求较完善或较适宜的方案,以期对工程实际应用提供理论指导[3-4].
本工作通过分析轨道吊结构中箱形主梁的结构和受力特点,在考虑主梁外载荷自重、惯性力及风载荷的基础上,建立主梁结构优化设计数学模型,并通过零阶算法,将结构刚度、强度和稳定性约束下的主梁自重极值问题转化成无条件约束下的极值问题,进而得到主梁几何参数的优化设计结果.所得结果表明本设计方法可以为充分利用结构部件的承载能力、控制结构重量提供参考.
1 轨道吊主梁结构
主梁作为轨道吊的主要承载构件,在工作过程中直接承受工作载荷,因此要求具有较高的强度、较好的稳定性以及尽可能小的自重.箱形双梁桥架是目前使用较广泛的主梁结构形式,具有制造简单、生产工效高、通用性强等优点,但也存在结构自重大、主梁容易下挠、桥架的水平刚度较差等缺点[5-6].因此,本工作拟对箱形双梁桥架形式的主梁进行优化设计,在减轻结构自重的同时,满足使用要求.
主梁的外载荷主要包括自重、惯性力和风载荷[7].
自重载荷为结构本身重量,即

式中,m为构件质量,g为重力加速度.
惯性力通过采用附加运动的机械加速度来计算,即

式中,a为构件运动加速度.
风载荷p1依据起重机设计手册提供的数据[8]来计算,即

式中,vs为风速,C为风力系数,A为构件正面迎风面积,ϕ为构件与风向的夹角.因为本工作假定风载荷是沿起重机最不利的水平方向作用的静力载荷,所以计算时取空旷地区高度10 m处的阵风风速(15.5 m/s).
2 轨道吊主梁结构的优化设计
2.1优化流程
现代优化设计方法是以最优化理论为基础,以计算机为手段,根据所追求的性能目标,建立目标函数,并在满足给定的各种约束条件下,寻求最优的设计方案.目前,常用的数值优化流程[9]如图1所示.
由图1可以看出,轨道吊结构的优化设计首先是确定优化设计参数,建立设计模型;然后将模型简化为有限元模型,并以结构强度、刚度和稳定性为设计约束条件,得到需要的优化结果.

图1 数值优化流程框图Fig.1 Flow chart of numerical optimization
2.2力学模型
本工作针对轨道吊主梁结构,以主梁结构整体强度、刚度及稳定性作为约束函数,并采用主梁翼缘板、腹板几何尺寸参数(如板长、板宽以及相应厚度等)作为设计变量,通过进行多参量优化分析,以期得到优化的主梁构件几何尺寸.轨道吊箱形主梁模型如图2所示,其中模型的设计变量可用一组相互独立的参数来表示:

式中,H为主梁高度,B为主梁宽度,T1和T2分别为上、下翼缘板的厚度,T3和T4分别为左、右腹板的厚度.
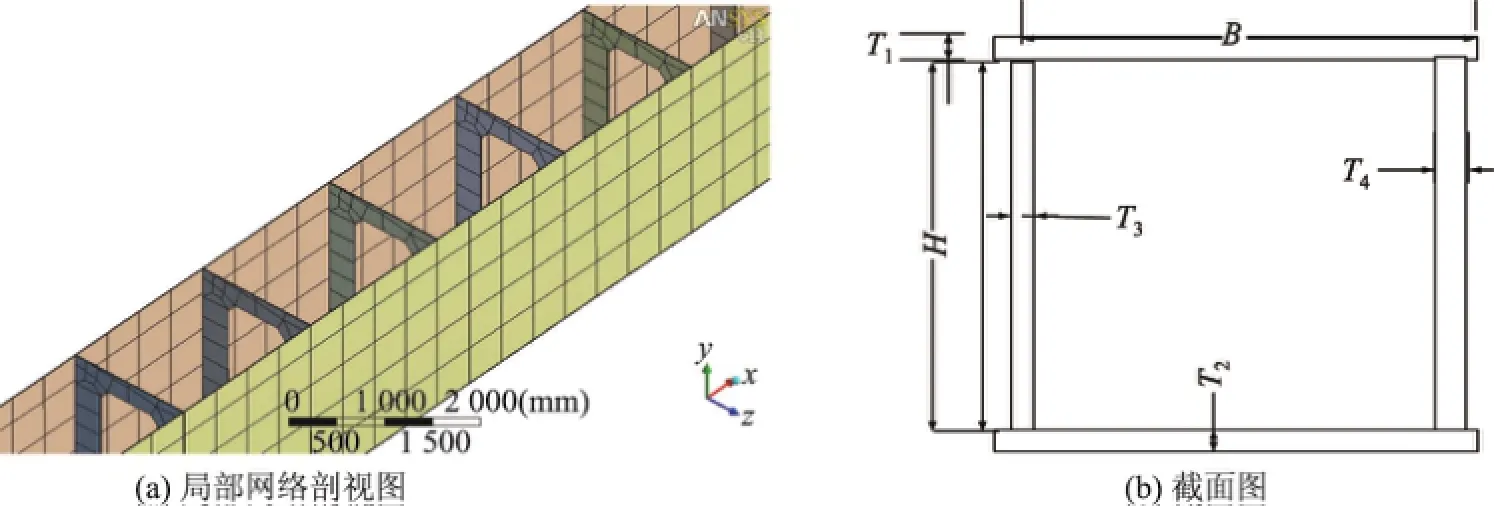
图2 轨道吊箱形主梁模型Fig.2 Model of the main beam for track hanging structure
因为在主梁跨度K固定的情况下,箱形主梁的自重和截面积成正比.因此,箱形主梁的体积(目标函数)为

根据起重机设计手册中的要求,主梁强度约束条件为最大应力不超过许用应力,即

式中,[σ]为结构许用应力.

主梁稳定性约束条件为优化后的屈曲特征值要小于原特征值,即

式中,λ0为优化前的屈曲特征值.
将目标函数与约束条件联立,可得如下方程组:

因此,通过求解式(9),可将相应的工程问题转换为力学约束条件下的最优解问题.
2.3基于零阶算法的优化方法
本工作采用零阶算法[10-11]求解上述力学约束条件下的最优解问题.零阶算法是在抽样统计的基础上,通过拟合设计变量、状态变量和目标函数的响应函数寻求最优解.
对于式(9)所示的约束极小值问题,设计变量可以取为


目标函数可以取为

式中,εg,εh,εw,εf为小参数.
工程问题一般采用平方拟合方法.式(11)和(12)的拟合公式为

根据式(11)~(13),约束极小值问题可写为如下形式:
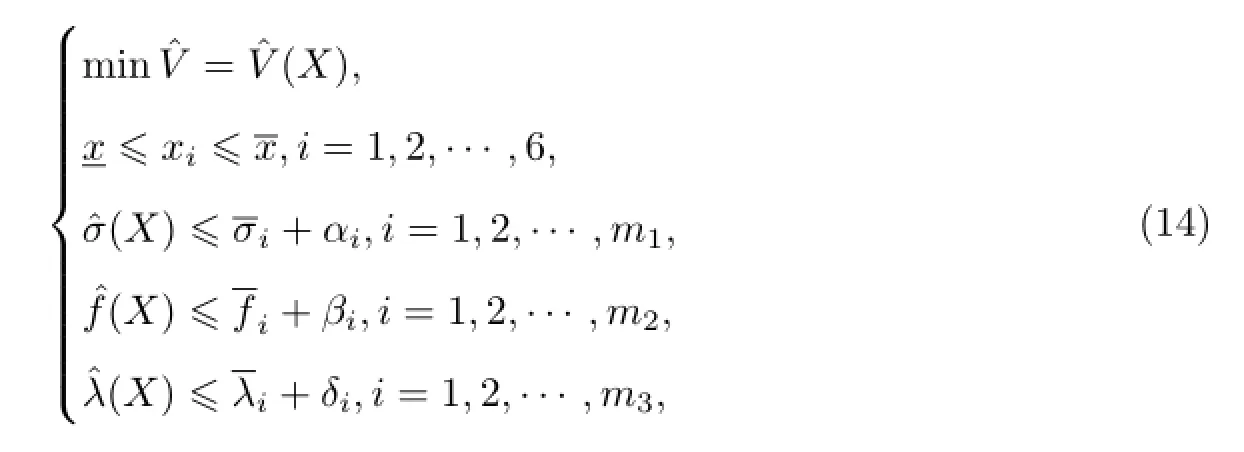
利用求约束条件下极值问题的拉格朗日公式[12-13],可将式(14)改写为
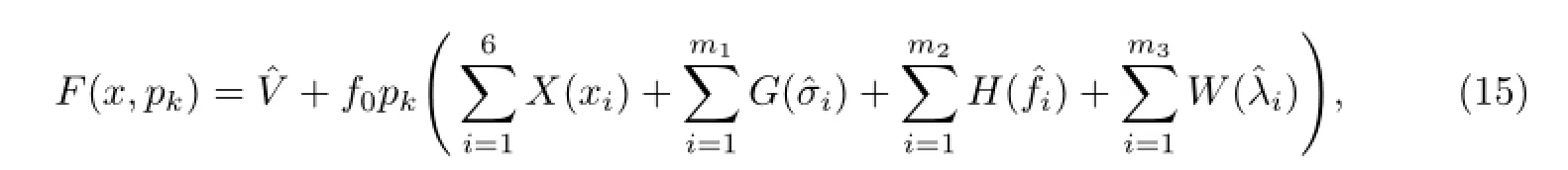
式中,xi为设计变量,f0为目标函数的参考值,pk为响应面参数,X为施加设计变量约束的罚函数,G,H,W为状态变量约束的罚函数.罚函数的形式如下:

式中,i=1,2,···,n,c1,c2,c3,c4为系数,ε为小参数.
通过式(14)~(16),可将约束条件及目标函数转化为无约束方程,再利用有限元数值计算方法,即可求得无约束极小化目标函数的优化解[14].
3 结果与讨论
通过参数化建模、求解,提取并指定优化变量和响应变量,再利用零阶优化方法,进行优化分析,计算求解得到相应的轨道吊主梁结构极值问题的设计变量优化值.相关的计算结果如表1所示.
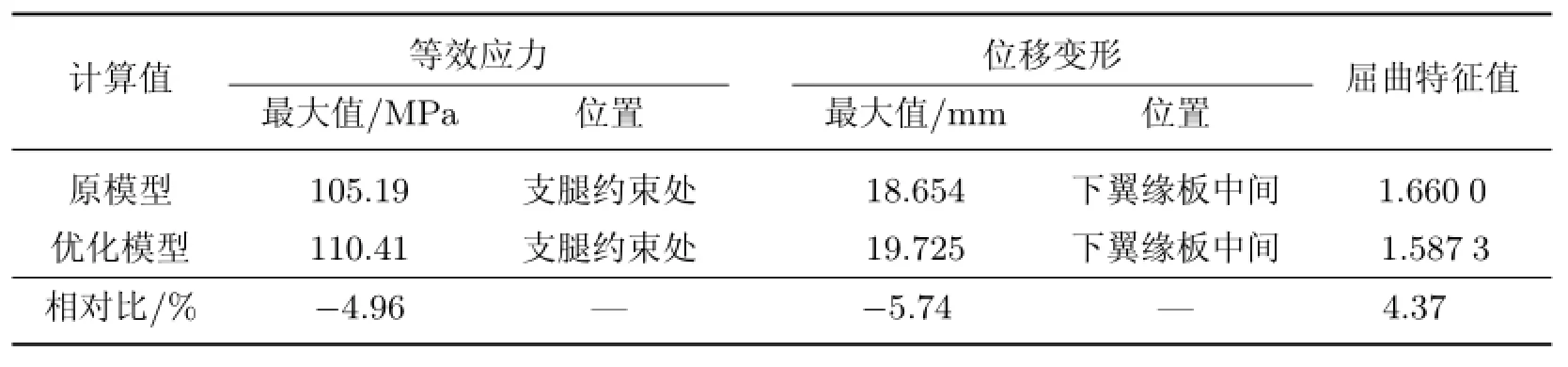
表1 主梁结构的计算特征量Table 1 Structural characteristic quantity for the main beam
由表1可以看出,主梁在优化前后的等效应力的最大值均出现在支腿约束处,二者仅相差4.96%;主梁在优化前后的最大变形均出现在下翼缘板中间,二者相差5.74%.主梁在优化前后的最大等效应力及位移均满足设计规范要求.主梁优化后的屈曲特征值变小,表明其整体及局部稳定性比优化前要好,并且高于安全系数.
表2为主梁结构的优化几何尺寸.可以看出,在满足强度、刚度和稳定性的约束下,优化构件的几何参数减轻了结构质量.与优化前的结构进行对比可知,上、下翼缘板厚度、主腹板厚度、主梁高、宽等尺寸均比优化前减小了约8%,而副腹板厚度仅增加了6.6%,最终主梁结构的质量减轻了20.28%.
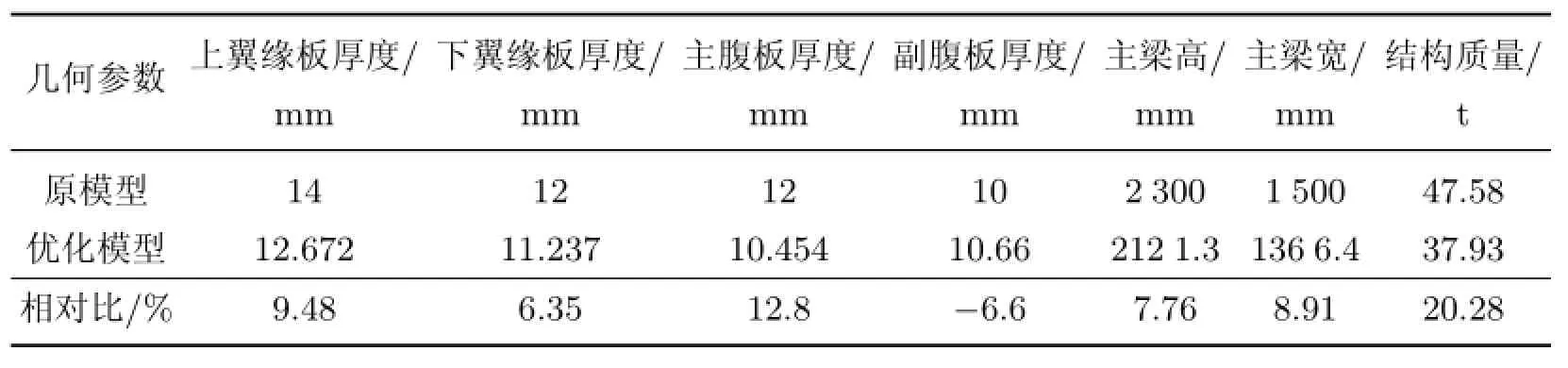
表2 主梁结构的优化几何尺寸Table 2 Optimization of the beam geometry
表3给出了构件各参数尺寸与等效应力、位移及屈曲特征值的相关度.相关度表示了结构尺寸对构件强度、刚度和稳定性的影响程度.主梁结构几何尺寸的相关度如图3所示.可以看出,主、副腹板厚度对强度影响较大;上、下翼缘板厚度和主、副腹板厚度对刚度影响较大;副腹板厚度、下翼缘板厚度、主腹板厚度对稳定性有较大的影响.在主梁结构强度、刚度和稳定性的综合要求下,副腹板厚度、主腹板厚度和下翼缘板厚度对主梁重量优化影响较大,而主梁的高和宽对强度、刚度及稳定性的影响较小.

表3 主梁结构几何尺寸的优化相关度Table 3 Relevance of the geometry optimization for the beam structure a.u.

图3 主梁结构几何尺寸的相关度Fig.3 Geometry relevance of the beam structure
4 结束语
本工作利用零阶算法将力学约束条件下的极值问题转化为无条件约束下的极值问题,并通过优化计算,将轨道吊主梁的相关几何参数进行了优化,在满足设计要求的条件下,减轻了主梁约20%的质量.
(1)通过优化计算,在保证结构刚度、强度及稳定性的前提下,主梁结构质量减轻达20.28%,主梁上、下翼缘板厚度,主腹板厚度、主梁高、宽等尺寸比优化前减小了8%左右,副腹板厚仅仅增加了6.6%.
(2)获得了相关几何尺寸的优化相关度,并通过相关度分析,得到了构件各尺寸对强度、刚度及稳定性的影响.主、副腹板厚度对强度影响较大;上、下翼缘板厚度、主、副腹板厚度对刚度影响较大;副腹板厚度、下翼缘板厚度、主腹板厚度对稳定性影响较大;主梁的高和宽对强度、刚度及稳定性的影响较小.
(3)通过力学建模、有限元计算和优化设计,可以合理利用结构部件承载能力、控制结构重量.在满足结构设计合理、安全的前提下,可实现产品精益制造,提高企业经济效益.
[1]程丽珠.桥式起重机主梁结构分析和优化设计[D].长春:吉林大学,2006.
[2]张晓丽,李明鹏,李跃华,等.桥式起重机主梁腹板结构拓扑优化设计[J].重庆工学院学报:自然科学版,2007,21(4):30-32.
[3]秦东晨,闫利利.桥式起重机箱形主梁的结构优化设计[J].矿山机械,2010,38(12):48-51.
[4]于兰峰.LDF型单梁桥式起重机小偏轨箱形主梁的优化设计[J].机械科学与技术,1996,15(2):198-202.
[5]赵小伟,卫良保.基于APDL的桥式起重机主梁快速优化设计[J].太原科技大学学报,2012,33(1):49-53.
[6]陶元芳,石小飞.基于改进微粒群算法的起重机主梁优化设计[J].中国工程机械学报,2012,10(1):50-53.
[7]郑玉巧,黄建龙,赵超凡.基于ANSYS的龙门起重机主梁力学性能分析[J].矿山机械,2010,38(11):60-62.
[8]《起重机设计手册》编写组.起重机设计手册[M].北京:机械工业出版社,1980.
[9]刘齐茂,燕柳斌.基于零阶和一阶优化算法的建筑结构抗震优化设计[J].华南地震,2008,28(4):27-34.
[10]郭彤,李爱群,王浩.基于牛顿-拉普森迭代和零阶优化算法的悬索结构找形研究[J].工程力学,2007,24(4):142-146.
[11]费景高.一类微分-代数系统实时控制的零阶保持算法[J].自然科学进展,2002,12(2):215-218.
[12]韩艳丽.约束优化问题的罚函数的研究[D].焦作:河南理工大学,2011.
[13]杜学武.求解约束优化问题的增广拉格朗日函数法[D].上海:上海大学,2005.
[14]郭彤,李爱群,费庆国,等.零阶与一阶优化算法在悬索桥模型修正中的应用对比分析[J].振动与冲击,2007,26(4):35-38.
Optimal design of track hanging structure using a zero-order algorithm
XIANG Qing1,YIN Zheng-nan1,QIN Hao2
(1.Shanghai Institute of Applied Mathematics and Mechanics,Shanghai University,
Shanghai 200072,China;2.Shanghai City Special-Purpose Equipment Surveillance and Inspection,Shanghai 200333,China)
Use of out of tolerance in hanging rail construction in engineering machinery usually causes inadequate utilization of the material and results in waste.Based on a mechanical analysis of the main beam structure in track hanging,a design optimization problem of weight of the girder structure is transformed to a solution of optimal parameters values under mechanical constraints optimal parameters.Using a girder flange plate and the web geometry value as input parameters,structural strength,stiffness,stability as response parameters,an optimization model is established based on a zero-order algorithm. Optimization results of the main beam are obtained by finite element numerical calculation. The results show that the new design method can reduce weight of the main beam and improve the efficient use of materials.
zero-order algorithm;track hanging structure;optimal design
TH 21
A
1007-2861(2015)06-0742-07
10.3969/j.issn.1007-2861.2015.03.003
2014-04-30
国家自然科学基金资助项目(10972128,11142004);上海市重点学科建设资助项目(S30106)
尹征南(1975—),男,讲师,博士,研究方向为冲击动力学、材料力学行为.E-mail:znyin@shu.edu.cn
