非均匀电场下乳化油中液滴变形动力学行为

陈庆国，宋春辉，梁雯，郑天宇，刘增，赵忠山，魏新劳



非均匀电场下乳化油中液滴变形动力学行为

陈庆国1，宋春辉1，梁雯1，郑天宇1，刘增2，赵忠山2，魏新劳1

（1哈尔滨理工大学工程电介质及其应用教育部重点实验室，黑龙江哈尔滨 150080；2大庆油田设计院，黑龙江大庆 163712）

外加电场下液滴的变形动力学行为是乳化液电脱水机理研究的重要内容。基于Cahn-Hilliard方程的相场方法，建立了液滴在非均匀电场下的仿真模型，研究了电场作用下乳化液中液滴在形变、移动和聚结过程中电荷密度和电场力的分布规律，以及流场和电场的耦合作用。仿真分析了液滴粒径、电场强度以及电场非均匀系数对液滴运动行为的影响。利用实验室小型脱水系统开展了乳化液脱水实验，并通过高速摄像机对乳化液中液滴的运动行为进行了观测与分析。研究结果表明，在非均匀电场中液滴表面的极化电荷分布不均，由液滴中部向两端逐渐增大，在靠近电场集中方向处的电荷密度和Maxwell应力值最大；在一定范围内增大电场强度、电场非均匀系数或液滴粒径，可使液滴形变量增大，液滴向电场集中区域的移动速度以及液滴间的聚结速度增加。

非均匀电场；相场方法；变形；动力学；聚结；数值模拟

引 言

原油电脱水因其高效和环保性被广泛应用，其脱水原理是原油乳液中的水滴在电场作用下合并成大水滴后沉降，实现油水分离[1-3]。国内外相关学者通过不同的实验方法和模型，对“油包水”型乳化液中水滴在电场作用下的脱水特性有了一定认识[4-9]。随着计算机的发展，数值模拟已成为重要的研究方法，如Feng等[10]通过有限元法研究了均匀电场中流体黏性对液滴变形规律的影响。Lac等[11]采用边界积分法，通过同时求解在均匀电场和流体场中的中性漏电液滴得到均匀电场中液滴的形变与稳定性规律。危卫等[12]通过VOF方法，研究了外加电场中中性漏电液滴和带电液滴形变的内在规律。梁猛等[13]通过Cahn-Hilliard方程的相场方法，研究了在匀强电场中，电场强度、液滴粒径和界面张力对液滴形变和破裂的影响。张军等[14]通过数值模拟研究了高压直流静电破乳过程中离散液滴群的运动规律。Kazimierz等[15]利用边界元素法研究了液滴在均匀电场中变形和破裂的动力学。张军等[16]通过耗散动力学方法对均匀电场下两相不相溶液体中的液滴变形特性进行了模拟。前述的实验研究和数值模拟中，均未涉及非均匀电场作用下液滴的迁移行为以及液滴表面极化电荷与液滴表面所受应力的分布情况，而且大多数的实验研究主要集中在实验分析方面，对外加非均匀电场下液滴的形变及力学行为和电场不均匀程度对乳化液脱水影响的研究很少。

本文采用Cahn-Hilliard方程的相场方法，建立了非均匀电场中的液滴模型，通过流场和电场的耦合作用，研究了液滴在非均匀电场中液滴表面极化电荷和液滴表面所受Maxwell应力的不均匀分布对液滴形变、位移和聚结的影响。并通过实验研究了电场强度、电场不均匀程度和液滴粒径对乳化液脱水的影响以及水滴在非均匀电场下的运动行为。研究结果可为乳化液在非均匀电场下的脱水特性研究奠定基础，指导陆上及海上油田高效原油电脱水器的设计。

1 仿真模型

1.1 电场模型

为研究液滴在非均匀电场下的形变和运动规律，通过多场耦合软件COMSOL Multiphysics 4.2a进行仿真分析。利用圆柱电极建立的电场模型的初始条件为内、外电极半径分别为1和2的同轴圆柱结构，在内、外电极间施加高压电场，仿真模型及仿真结果如图1所示。

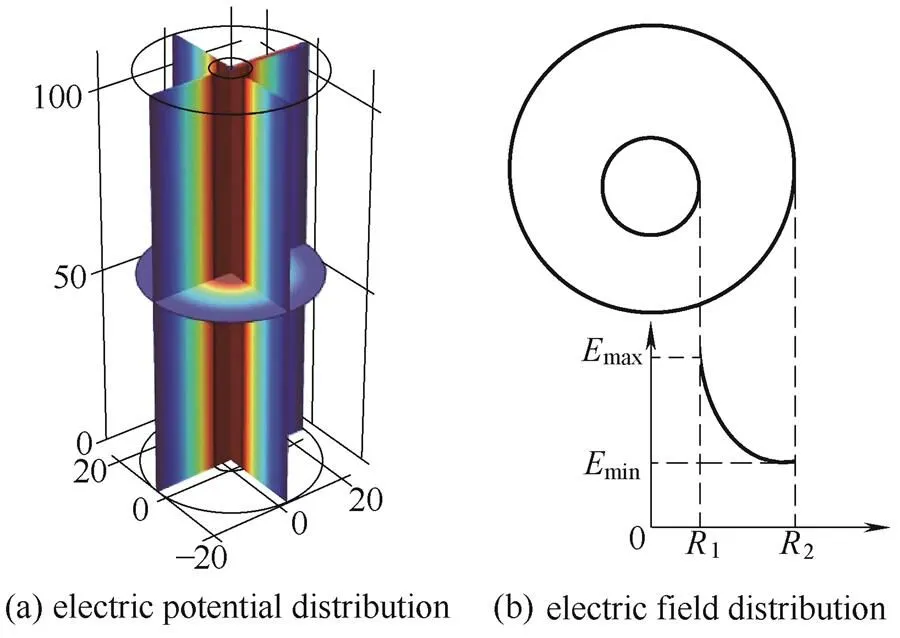
图1 同轴圆柱电极结构仿真

从图1中可以看出，沿半径方向随着偏离圆心程度的增加，电势逐渐降低；圆柱电极形成的是非均匀电场，电场强度分布和电势分布一致，且在内外电极间任意等径柱面上的电场强度相同。

电流体动力学中产生的动态电流通常比较小，因此可以忽略磁效应的影响。在交流电场中，电流密度可表示为传导电流密度和位移电流密度之和，写为以下形式

在静电场作用下，分散相中的液滴所受的电场力可由Maxwell应力张量表示

Maxwell应力张量可表达为

可知，电场力可表达为

其中，式(5)等号右侧第1项是表面电荷与电场作用的体积力，沿着电场线方向；第2项是电场的极化应力，它沿着流体与周围介质界面的法向方向；第3项是由于介质密度变化引起的，本文假设流体为不可压缩，该项可忽略。

1.2 液滴模型

假设液滴的初始形态为球体，仿真过程中液滴悬浮于油中，所建立的模型如图2所示。

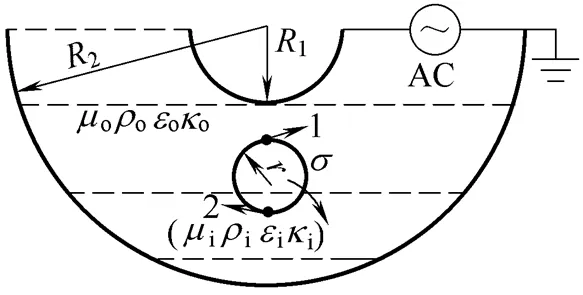
图2 液滴悬浮于油中的仿真模型

图2为一个半径、黏度i、密度i、相对介电常数i、电导率i的液滴悬浮于黏度o、密度o、相对介电常数o、电导率o的绝缘油中，液滴与油的界面张力为，点1和点2为液滴模型沿电场线方向的数据采样点。

电流体动力学中，流体运动受到耦合的惯性力、黏性力和电场力支配[17]，这些力影响流体的运动状态。假设液滴与周围的油互不相溶，且液滴和油均为不可压缩流体，由流体运动的动量平衡定律和质量守恒定律可得

黏性切应力张量可以表示为

在分散相液滴的变形动力学研究中，分散相与连续相的界面变化是研究关键，本文采用相场方法模拟界面运动，该方法通过微分方程反映相变过程中的扩散、有序化势以及热力学驱动力的综合作用，用其解来描述相界面的形态、曲率以及界面的移动[18]。

相场方法的控制方程可表达为

其中，变量表达式为

单位体积界面张力矢量st作为动量守恒方程式(6)的源项，其与的关系为

在利用相场方法进行两相流模拟时，通过求解方程式(9)的解来描述相界面的形态、曲率以及界面的移动，可以实现两相流界面的追踪。

2 仿真结果与讨论

假设液滴显电中性（未考虑液滴在位移过程中接触电极荷电过程），在仿真过程中，分散相与连续相的初始设置为：液滴直径为4 mm，界面张力为29 mN·m-1，连续相黏度为14.5 mPa·s，密度为880 kg·m-3，液滴密度为960 kg·m-3，水滴电导率为5.5 μS·m-1。在电极间施加频率为50 Hz的正弦交流高压，使液滴处于电场强度为4 kV·cm-1的电场中，仿真分析得到液滴在交流电场中主要发生形变、位移和聚结3种运动行为。

2.1 液滴形变与位移

液滴在一周期20 ms内的形变以及在0.15 s内的运动情况分别如图3、图4所示。

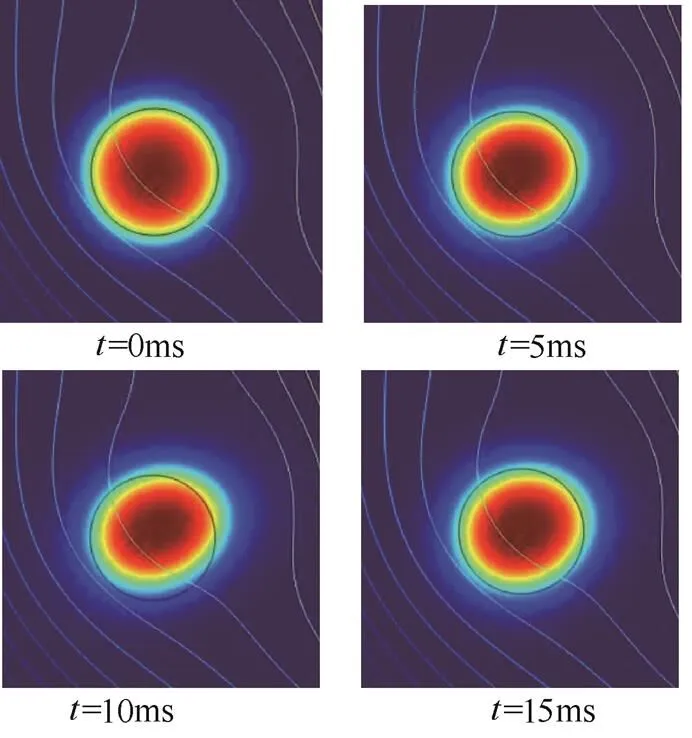
图3 单液滴振荡形变

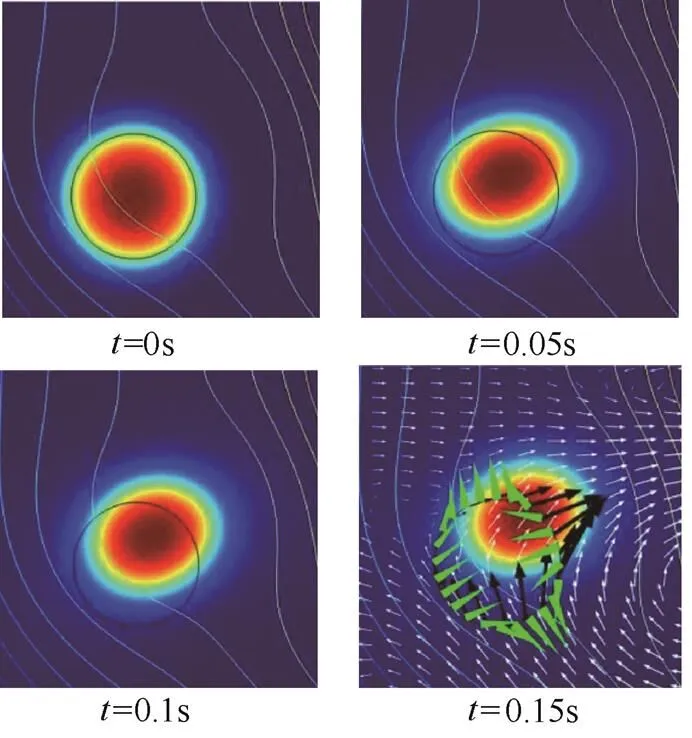
图4 液滴位移及流体速度矢量分布

从图3可以看出，在电场作用下，液滴形态在球形和椭球形之间不断变换，说明液滴沿电场线方向发生振荡。从图4中可以看出，在非均匀电场下，液滴沿电场线方向发生形变的同时向场强集中处发生位移。在0.15 s时刻，箭头表示速度矢量分布，其中白色箭头表示液滴周围流体速度矢量，黑色箭头表示液滴表面速度矢量，锥形箭头表示液滴受到的黏性应力矢量分布。从分布图中可以看出，液滴在形变过程中受到周围流体对其产生的黏性应力作用，阻碍液滴变形；但液滴所受到的电场力大于阻力，致使液滴继续向场强集中处移动。

为了进一步研究液滴形变的根本原因，对液滴表面电荷密度的分布情况进行仿真，仿真结果如图5所示。

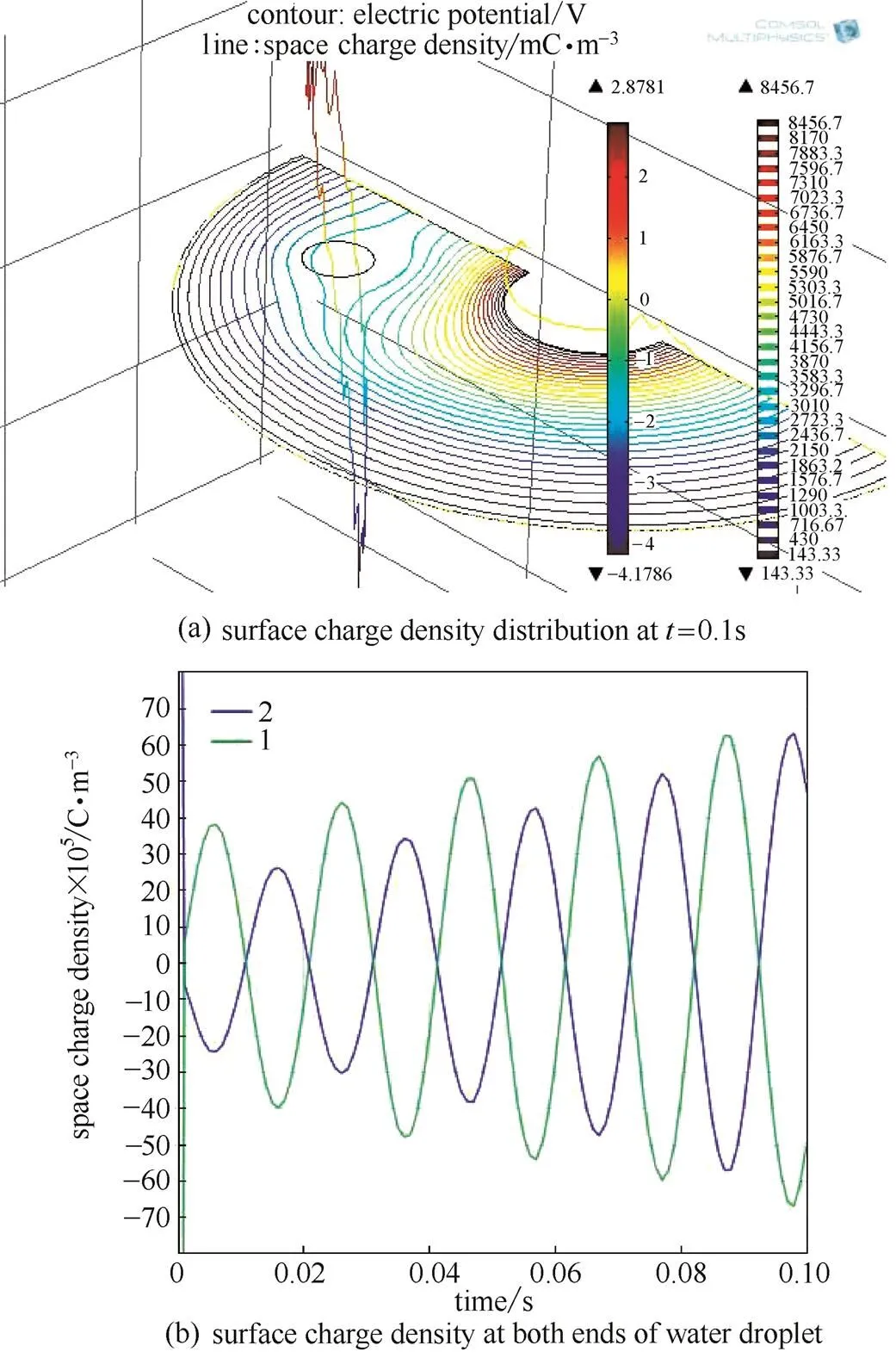
图5 液滴表面电荷密度随时间分布曲线

从图5 (a)可以看出液滴极化电荷密度由液滴中部向两端逐渐增大，在场强集中处，极化电荷密度增大速度较快，靠近场强集中的端部电荷密度最大；从图5 (b)可以看出，在交变电场下，电荷密度随电场强度变化而变化，当电场强度增加时，电荷密度增大。

通过仿真分析可以得出，液滴形变主要受到其电荷密度分布和电场强度变化的影响。在非均匀电场作用下，由于电荷密度主要分布在液滴两端，且在电场强度集中处的端部达到最大，因此液滴沿电场方向拉伸，并在电场强度集中处产生最大形变。随着电场强度的变化，电荷密度也随之增加或减少，使液滴沿电场方向产生振荡。

为了进一步研究液滴位移的根本原因，对液滴沿电场方向受到的Maxwell应力分布情况进行仿真，仿真结果如图6所示。

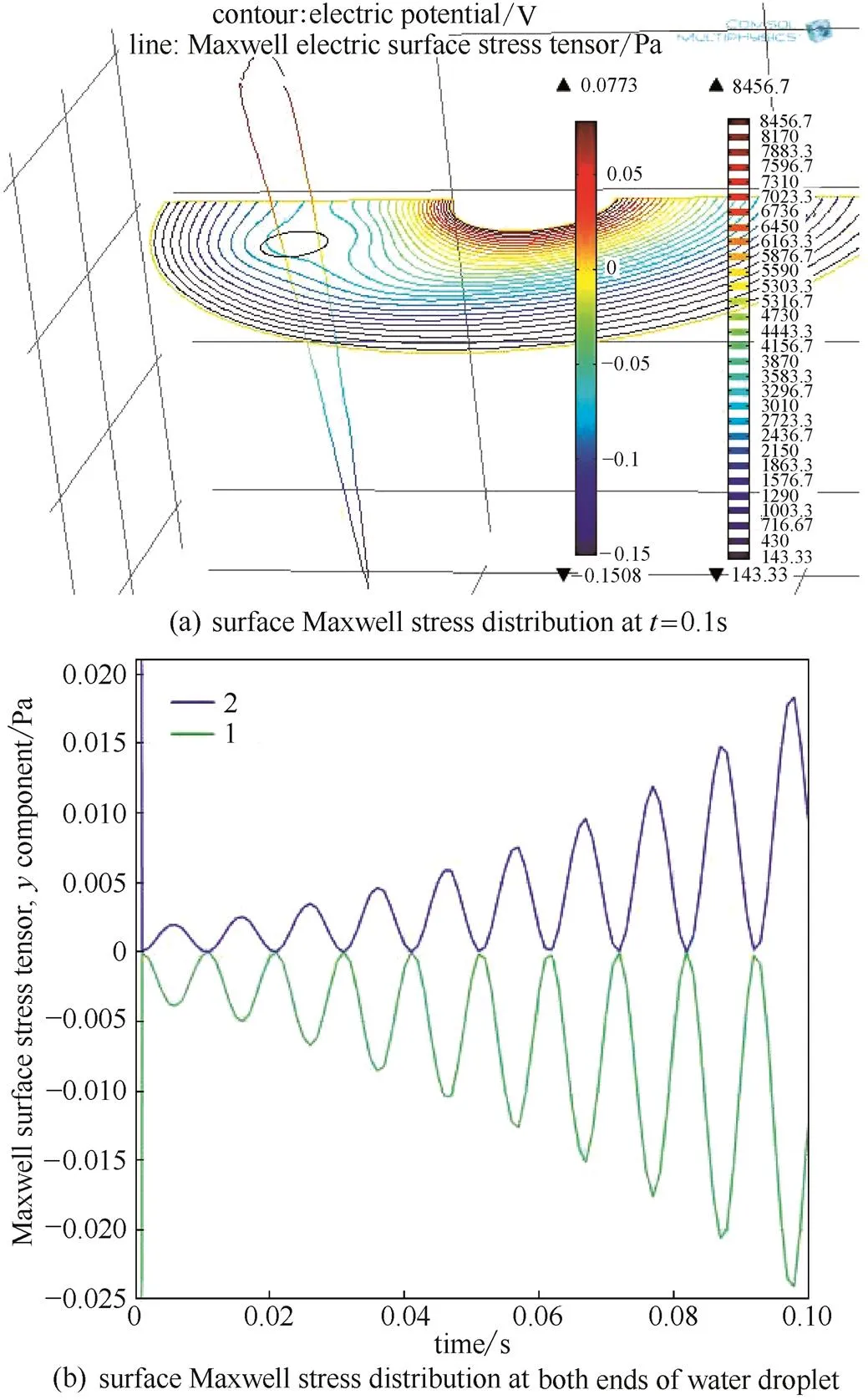
图6 液滴表面Maxwell应力

从图6 (a)可以看出，液滴表面Maxwell应力分布与电荷密度分布相似，在液滴最靠近电场集中方向的端部产生的应力最大，且从液滴中部逐渐向两端增大；从图6 (b)可知，液滴两端受到的应力大小不同，这是由于非均匀电场作用下液滴表面极化电荷密度分布不同、不同位置的电场强度大小不同，因此液滴在点1处所受到的应力大于在点2处所受到的应力，液滴整体所受合力不为零，使得液滴向电场集中处移动。随着液滴的移动，所处位置的电场强度逐渐增大，液滴所受合力也逐渐增大，从而加快了液滴的移动速度。

2.2 液滴聚结

液滴在0.15 s内的聚结情况如图7所示。

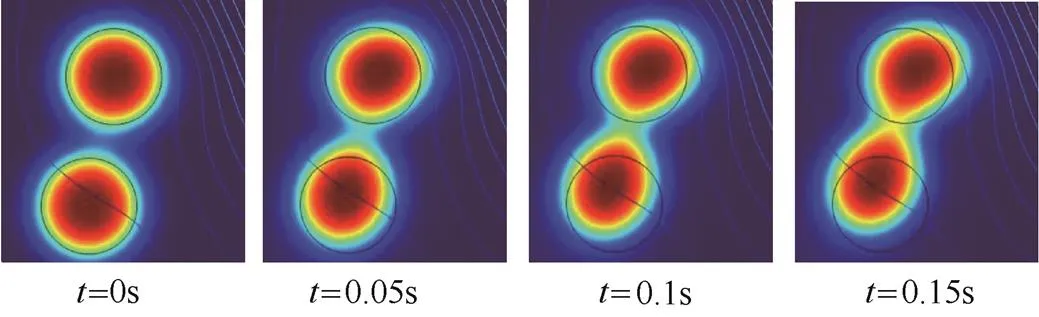
图7 液滴聚结情况

从图中可以看出，在非均匀电场作用下，液滴在发生聚结的同时也沿着电场线方向向电场强度集中处移动。

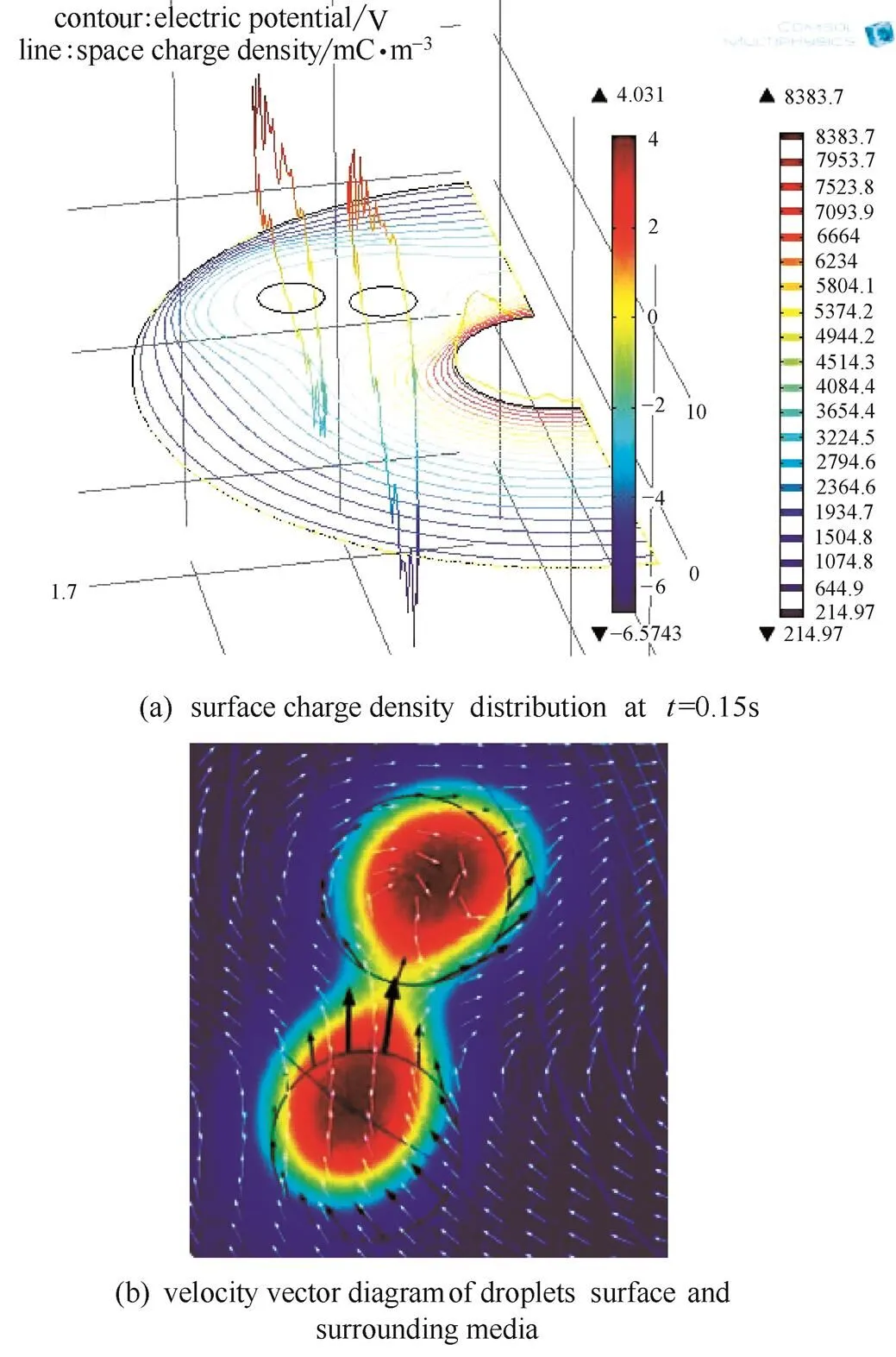
图8 液滴表面电荷密度和速度矢量图

从图8 (a)可以看出，液滴相互靠近的端部处极化电荷极性相反，使得液滴之间存在偶极吸引作用。从图8 (b)可以看出，液滴对在聚结过程中的形变量大于单液滴时的形变量。通过图中代表流体速度矢量分布的白色箭头可知，在电场力作用下，流体克服流动阻力从液滴两侧流向端部，使得连续相间产生湍动，液滴内部形成环流，加强了液滴的形变。通过图中黑色箭头代表的液滴表面速度矢量分布可以看出，原本要向电场强度密集处移动的液滴，在偶极力作用下改变了运动方向，向靠近自己的液滴方向移动，从而使两个液滴间发生聚结；若液滴所受到的偶极力小于电场力，有可能会发生液滴对间距增加的情况。

3 液滴运动行为的影响因素分析

3.1 电场强度及其分布对液滴运动行为的影响

为研究电场强度对液滴形变的影响，得到半径为2 mm的液滴在电场强度为2、4、6、8、12 kV·cm-1下的最大形变分别如图9 (a)～(e)所示。

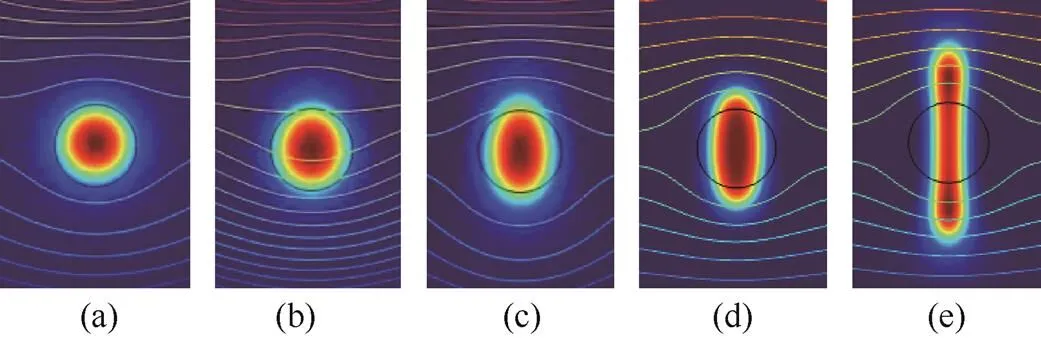
图9 不同电场强度下液滴形变

从仿真结果可以看出，随着电场强度的增大，液滴最大形变程度变大，当场强提高到一定程度时液滴形变过大易出现破裂。

液滴最大形变量随电场强度的增大有明显增大，这是由于液滴在电场作用下产生的极化电荷量与电场强度呈正比，而液滴受到的电场力为极化电荷与场强的乘积，所以当电场强度增大时，液滴所受电场力变大，液滴最大形变量增加。

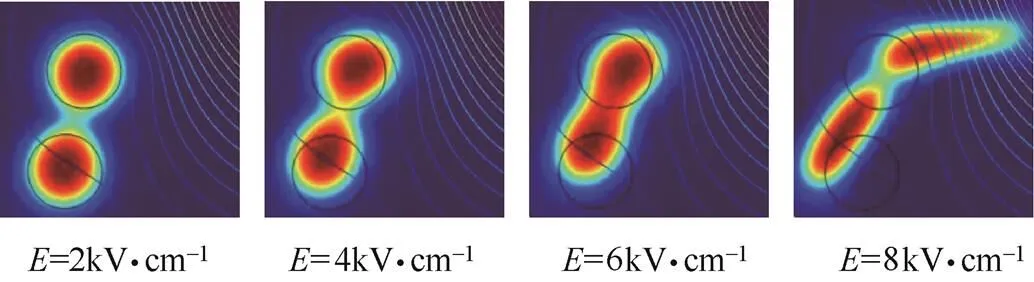
图10 不同场强下液滴聚结情况

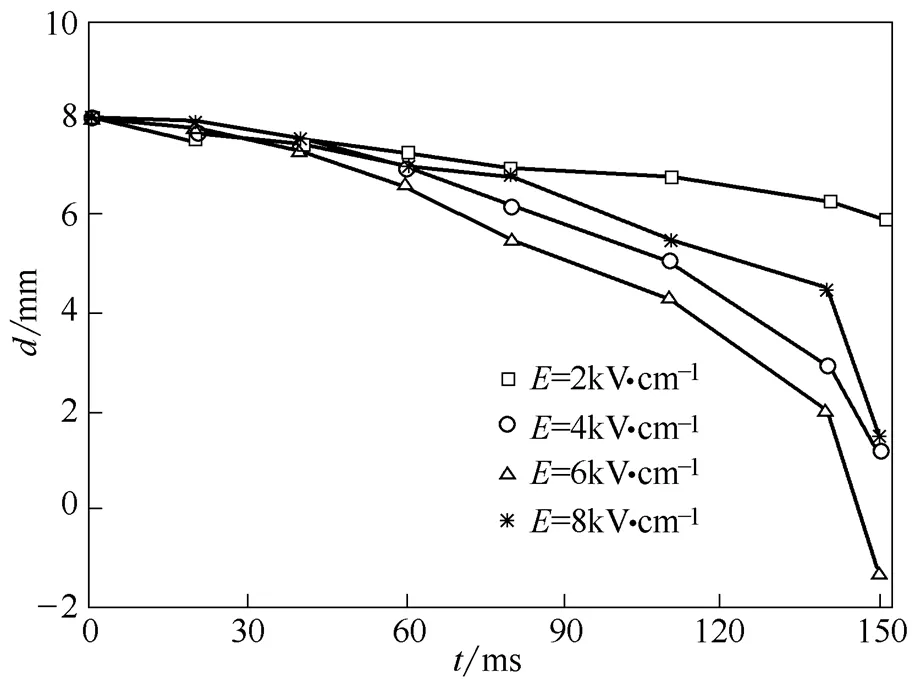
图11 不同电场强度下液滴间距随时间的变化

从仿真结果可以看出，随着电场强度的增大，液滴间的靠近速度逐渐加快，当电场强度增大到一定程度后，液滴间靠近速度变慢。这是因为，影响液滴间距的主要因素为偶极吸引力和介电泳力，当电场强度在一定范围内时，偶极力对液滴的影响大于介电泳力，此时随着电场强度的增大，液滴间距逐渐减小；当电场强度增大到一定程度时，液滴受介电泳力影响较大，介电泳力迫使液滴向场强集中处移动，靠近场强密集处的液滴移动速度快，导致两液滴间距逐渐增大，液滴聚结时间增长，所以过高的电场强度不利于液滴聚结。

证明：应用推论2.取显然an≠0且an→0(n→∞),bn≠0且从而于是函数在点x=0没有极限。证明非常好，值得重视！

为了研究非均匀电场中，电场集中程度对液滴运动行为的影响，将液滴模型分别放置在场强分布不同的电场1和电场2中进行仿真分析，同时保证液滴所处位置的电场强度相同。

电场1和电场2的分布如图12所示。

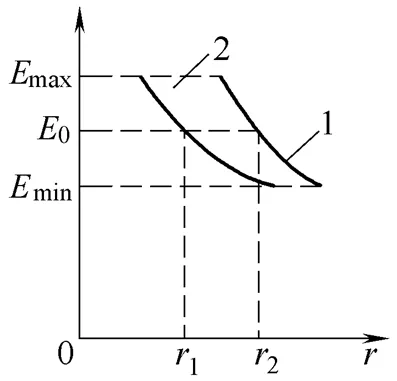
图12 不同非均匀度的电场分布曲线

从图12可知，电场1场强变化率大于电场2，电场非均匀度更大。将液滴模型分别放置在电场强度为0的1、2处，得到液滴在0.15 s内的形变及位移情况分别如图13 (a)、(b)所示。

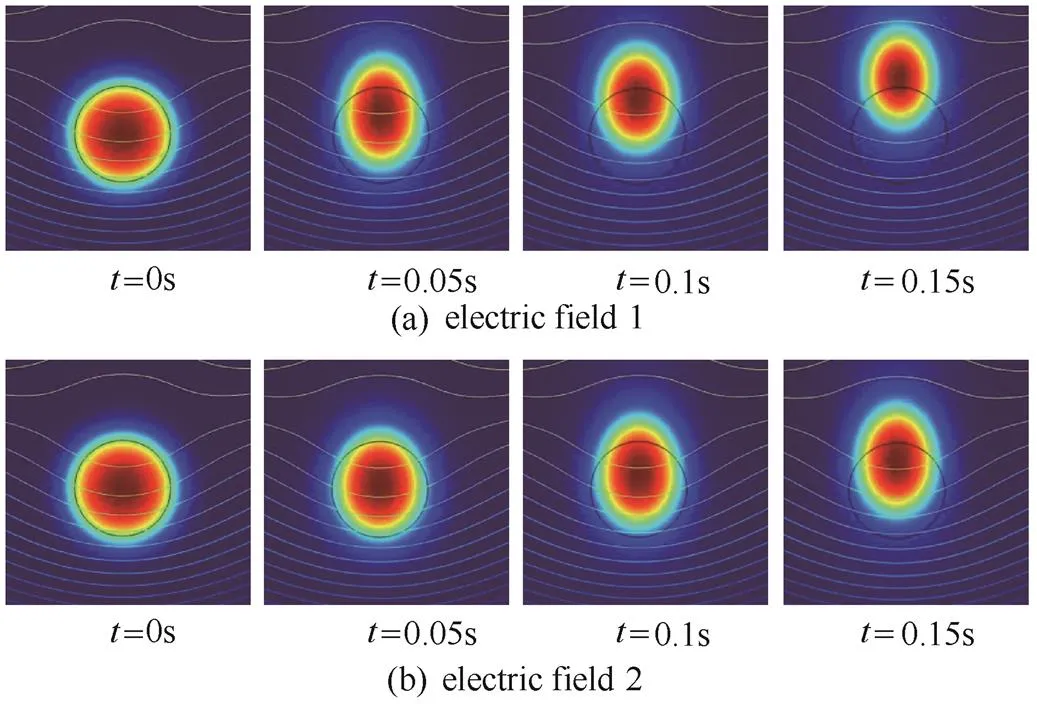
图13 不同梯度电场下液滴的形变及位移情况

从仿真结果可以看出，液滴最大形变量以及位移受电场强度和场强分布的影响较明显。

液滴在电场1中的位移和液滴形变量均大于在电场2中。在0 s时刻，液滴受到电场力作用开始移动，由于电场1中的电场梯度较大，在下一时刻液滴所处位置中的电场强度和本身的极化电荷量都大于电场2，所以液滴在电场1中所受的电场拉力和合力都大于电场2，进一步导致了液滴形变量和位移量的增大。

3.2 液滴直径对形变量的影响

为了定量体现液滴形变程度，定义液滴形变度为[19]

通过仿真计算得到液滴在不同半径时其形变度与电场强度关系如图14所示。

从图14可知，当电场强度由2 kV·cm-1增大到8 kV·cm-1时，半径为1.5 mm的液滴形变度由0.15增大到0.82，半径3 mm的液滴形变度由0.32增大到0.9；液滴粒径越大，所受电场强度越高，液滴形变量越大。

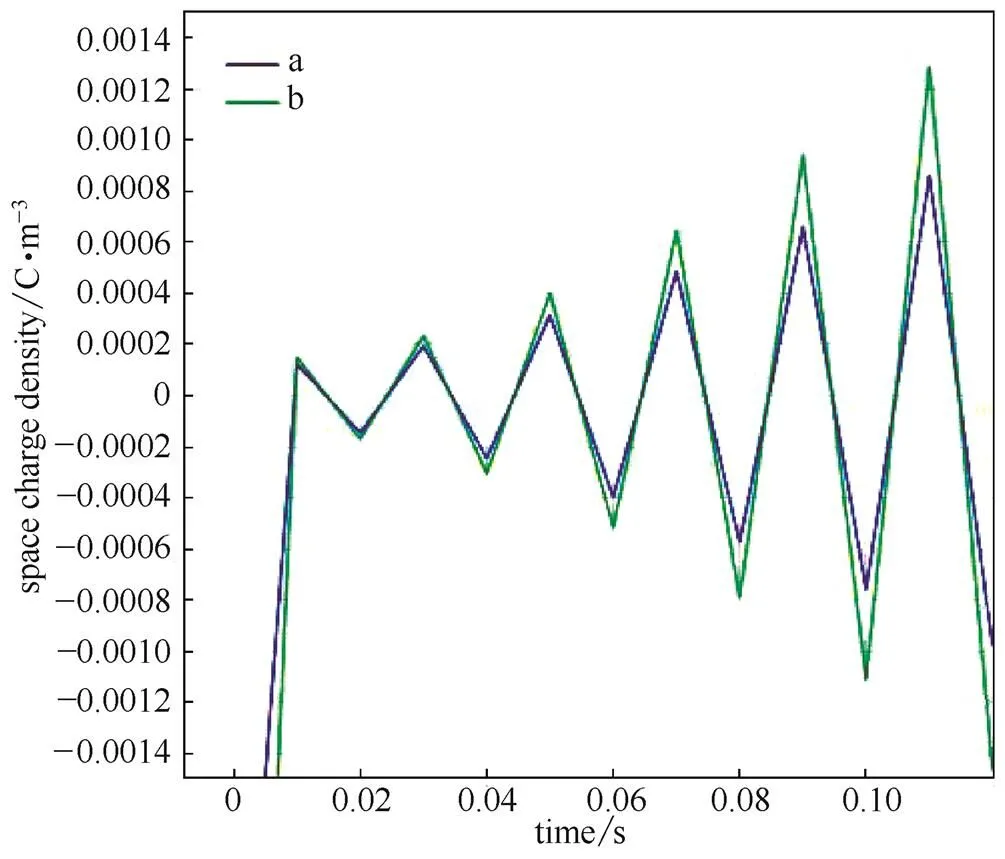
图15 液滴表面电荷密度随时间的变化

从图15中可以看出，大液滴b处比小液滴a处极化出的电荷密度大，可知在相同电场强度作用下，液滴粒径越大产生的极化电荷越多，使得液滴受到的电场力越大，形变量越大。由此可知在相同条件下，粒径大的液滴形变大，液滴接触时偶极吸引力大，液滴之间的聚结速率更快。

4 脱水实验研究

4.1 实验系统与方法

乳化液脱水实验系统如图16所示，它由混合罐、乳化机、计量泵、电脱水器、废液罐和高速摄像机组成。调配罐设有夹层，便于导热油循环使乳化液加热至实验所需温度；乳化机为转速范围在0～30000 r·min-1的ESB-500型实验室高剪切均质乳化机；脱水电源由高压工频交流供电装置提供，其幅值调节范围为0～15 kV；乳化液电脱水微观实验现象采用MS55K型高速摄像机拍摄记录，并与计算机相连进行图片处理。脱水电极由同轴空心不锈钢管构成，内电极接高压，外电极接地。

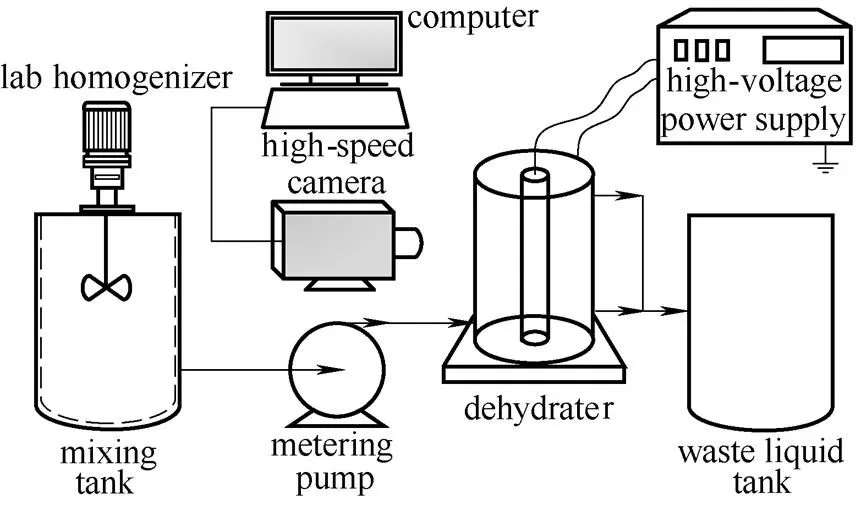
图16 乳化液脱水实验系统

实验用油选择工业白油，25℃时其密度为877 kg·m-3，动力黏度为14.5 mPa·s，与水的界面张力为29 mN·m-1。为了得到稳定的含水率为10%的乳化液，实验时将白油与蒸馏水按9:1的体积比例混合倒入调配罐中，加入体积分数为1%的Span-80乳化剂，通过乳化机将油水混合液乳化，形成均相稳态的乳化液。然后开启计量泵将液体泵入脱水器内进行电脱水实验，通过水分测定仪测量试样的含水率。

在进行乳化液电脱水实验中，脱水率是衡量脱水效果的指标，脱水率可按式(13)进行计算

对于同轴圆柱电极，当内半径与外半径之比小于1/时为极不均匀电场，大于1/时为稍不均匀电场，为了定量体现电场非均匀程度的大小，引入非均匀系数，其表达式为[20]

实验中采用的3种电极参数如表1所示。

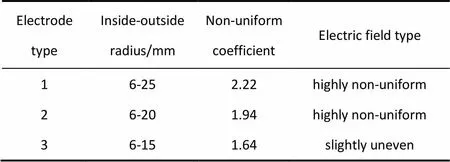
表1 电极尺寸及其不均匀系数

4.2 实验结果与分析

4.2.1 乳化液中液滴的运动情况 为了分析液滴在非均匀电场中的运动情况，在圆柱电极中充满模拟油，滴入半径为溶解少量水溶性红色染料的水滴，施加高压。实验过程中利用高速摄像机以100帧/秒的速度进行拍摄，利用LED灯对液滴进行了补光拍摄，得到水滴的运动及形变情况如图17所示，图中左侧电极施加高压，右侧电极接地。

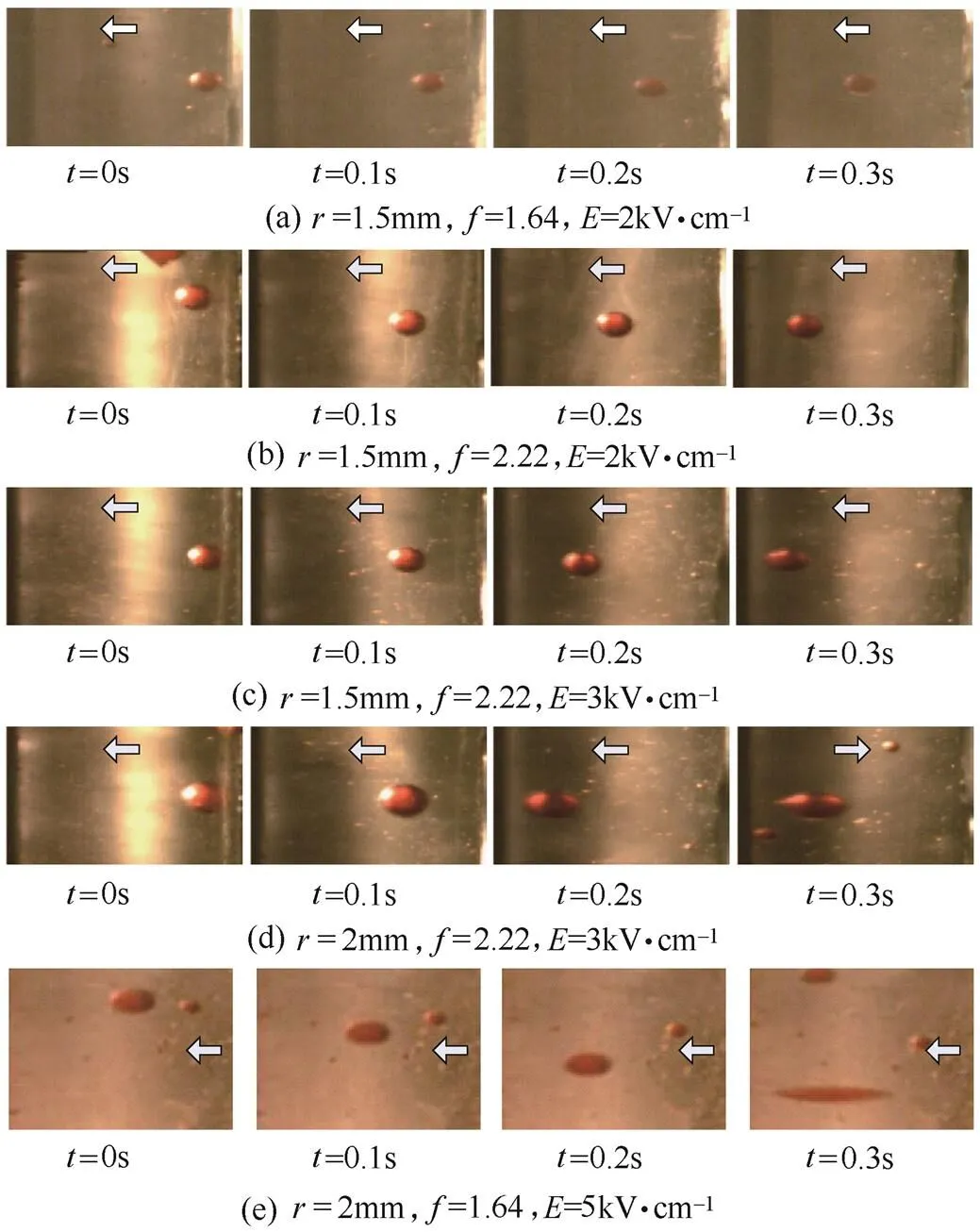
图17 水滴在非均匀电场中的运动

从图17 (a)、(b)中可以看出，电场非均匀系数越大，液滴向场强集中处移动的速度越快；从图17 (b)、(c)中可以看出，随着场强的增大，液滴运动速度增加；从图17 (c)、(d)中可以看出，在相同时间内半径大的液滴比半径小的液滴运动速度快，且形变量大；从图17 (e)可以看出，液滴在高场强下形变量较大，易发生破裂。

通过以上分析可知，液滴受到介电泳力和形变程度与电场强度有密切关系，当电场越集中、电场场强越大、液滴半径越大，液滴所受介电泳力越大，液滴运动的速度越大，液滴形变越大。

为了分析液滴在非均匀电场中的聚结情况，向极板两端分别施加3 kV·cm-1和6 kV·cm-1的交流电场后得到液滴之间的聚结情况如图18所示。

图18 水滴在非均匀电场中的聚结

从图18 (a)中可以看出，在3 kV·cm-1场强下液滴对在约0.3 s内完成了接触、排液和聚结的整个聚结过程。在图18 (b)中，两液滴在0.2 s时刻发生聚结，随后和第3个液滴发生聚结，但由于聚结后的液滴粒径较大，在拉伸后容易发生破裂，所以提高电场非均匀系数虽然可以加大液滴形变量、加快液滴的聚结速率，但也容易造成大液滴的破裂。从图18 (c)中可以看出，在6 kV·cm-1的场强作用下，虽然液滴形变量有所增加，但两个液滴在向电场强度密集处移动的过程中，相对距离逐渐增大，最终并未发生聚结。这是因为，在较高电场强度下，液滴受介电泳力影响较大，向电场集中处移动的速度较快，导致了两液滴间距的增加，使得液滴接触聚结时间变长。

4.2.2 电场强度及其分布对乳化液脱水的影响 为研究电场强度和电场不均匀程度对乳化液脱水效果的影响，以圆柱电极平均场强衡量外施场强的大小，平均场强av的表达式为[20]

在非均匀系数为2.22、1.94和1.64，平均场强av分别为3 kV·cm-1和6 kV·cm-1的电场作用下，对含水率为10%的乳化液进行脱水实验，得到乳化液脱水率随时间变化曲线如图19所示。

在图19中，不同电场下乳化液脱水率达到80%时所用脱水时间如表2所示。

表2 不同电场强度下脱水率为80%所用时间

从图19和表2可以看出，随着非均匀系数和脱水电场的增加，脱水速率加快；非均匀系数对脱水速率的影响比电场强度的影响更显著。不同电场强度下乳化液最终含水率如表3所示。

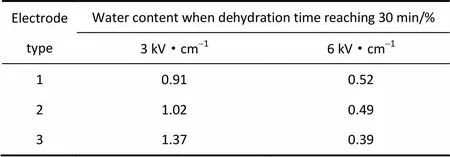
表3 不同电场强度下的最终含水率

由表3可以看出，随着非均匀系数和脱水电场的增加，最终含水率均相应减小；电场强度对最终含水率的影响比非均匀系数的影响更明显。在高场强（6 kV·cm-1）下，电场非均匀系数的提高有利于最终含水率的降低，但过高的非均匀系数造成电场的高度集中容易导致电分散现象的发生，不利于脱水的进行。

4.2.3 液滴直径对乳化液脱水的影响 剪切速率对乳化液中液滴粒径影响较大，实验过程中通过电子显微镜观察到剪切速率分别为5000、10000、20000 r·min-1时，乳化液中局部液滴分布如图20所示。

图20 不同转速时液滴分布

从图20可以看出，随着剪切机转速的升高，液滴平均直径变小，在转速为5000、10000、20000 r·min-1下，液滴平均直径分别为15.96、9.54、5.89 μm。实验得到非均匀系数为2.22、平均场强为3 kV·cm-1电场下，不同剪切速率下乳化液脱水率随时间变化曲线如图21所示。

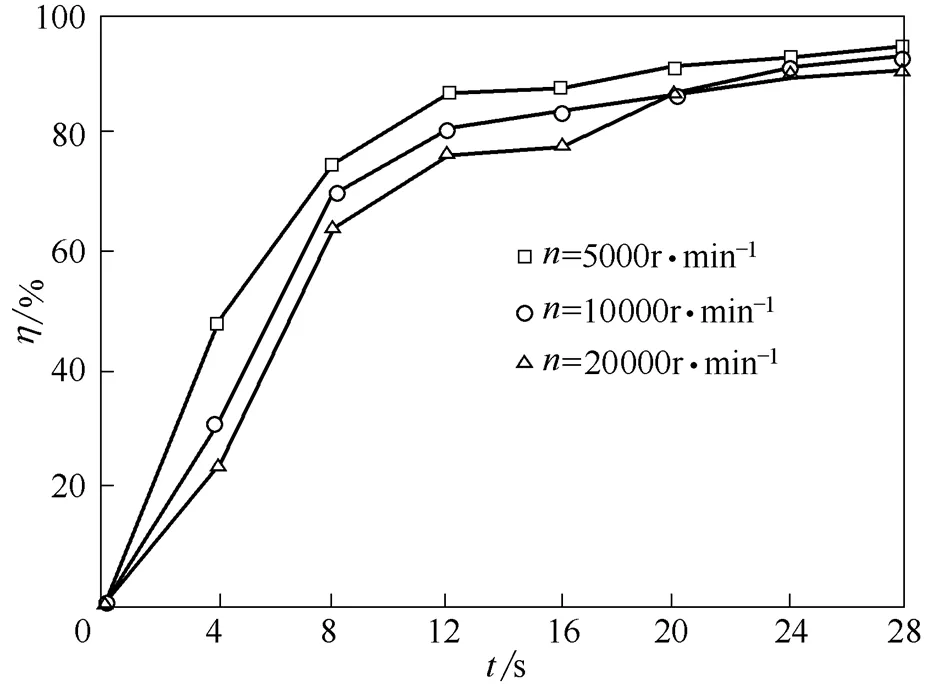
图21 不同转速乳化液脱水率随时间的变化

从图21中可以看出，随着液滴直径的增大，乳化液的脱水效率逐渐增大。在同一电场强度下，液滴直径越大，形变量越大，液滴之间的偶极吸引作用越大，两液滴越容易发生聚结，使脱水时间变短，这一实验结果与仿真结果一致。

5 结 论

本文借助仿真手段，采用将流场和电场相耦合的方法，研究了单液滴的形变和双液滴的聚结行为，对影响液滴聚结速率的因素进行了分析，并通过实验验证了仿真结果的准确性，得到结论如下。

（1）在非均匀电场中，液滴表面极化电荷分布不均，由液滴中部向两端逐渐增大；在靠近电场集中方向处的电荷密度和Maxwell应力最大。

（2）乳化液中液滴的形变以及力学行为取决于流场和电场共同的作用，且电场强度越大，电场越集中，液滴粒径越大，液滴极化电荷越多，形变越大，液滴受介电泳力越大，向电场集中处位移速度越快，液滴间聚结速率越快。

（3）通过脱水实验和高速摄像机的观测可知，在一定范围内，可通过提高非均匀系数、提高电场强度、增大液滴直径等手段提高乳化液中液滴的聚结速率；当电场强度过高，非均匀度过大时，液滴受到的电场力和介电泳力过大，容易导致液滴发生破裂，降低了液滴对的聚结效率。

符 号 说 明

D——液滴形变度，% d——液滴间距，m E——外施电场强度，V·m-1 Eav——平均电场强度，V·m-1 Emax，Emin——分别为电场强度最大、最小值，V·m-1 F，Fst——分别为电场力、表面张力，N·m-3 f——电场非均匀系数 G——化学势，J·m-3 g——重力加速度，m·s-2 h——界面厚度，m I——单位矩阵 J——电流密度，A·m-2 l1，l2——分别为液滴椭圆时的长轴、短轴长度，m P0，Pt——分别为乳化液初始时刻、t时刻含水率，% p——流体压力，Pa R1，R2——分别为圆柱电极内半径、外半径，m r——液滴半径，m T——Maxwell应力张量，N·m-2 V——流体速度矢量，m·s-1 γ——控制Cahn-Hilliard方程扩散尺度的迁移系数，m-3·s·kg-1 εr——相对介电常数 ε0——真空介电常数，8.85×10-12 F·m-1 h——乳化液脱水率，% κ——流体电导率，S·m-1 l——混合能量密度，N μ——流体黏度，Pa·s ρ——流体密度，kg·cm-3 ω——电场角频率

References

[1] Feng Shuchu (冯叔初), Guo Kuichang (郭揆常). Oil & Gas Gathering Transportation and Processing in Mines (油气集输与矿场加工) [M]. Dongying: China University of Petroleum Press, 2006

[2] Chen Qingguo (陈庆国), Liang Wen (梁雯), Song Chunhui (宋春辉). Effect of electric field strength on crude oil emulsion’s demulsification and dehydration [J].(高电压技术), 2014, 40 (1):173-180

[3] Yang Donghai (杨东海), He Limin (何利民), Ye Tuanjie (叶团结), Luo Xiaoming (罗小明). Factors influencing single drop deformation in high-voltage AC electric field [J].(化工学报), 2011, 62 (5): 1358-1364

[4] Eow John S, Ghadiri Mojtaba, Sharif Adel. Experimental studies of deformation and break up of aqueous drops in high electric fields [J].:.,., 2003, 22 (5): 193- 210

[5] Graeme Supeene, Charles R Koch, Subir Bhattacharjee. Deformation of a droplet in an electric field: nonlinear transient response in perfect and leaky dielectric media [J]., 2008, 31 (8): 463-476

[6] Kazem Alinezhad, Morteza Hosseini, Kamyar Movagarnejad, Mehdi Salehi. Experimental and modeling approach to study separation of water in crude oil emulsion under non-uniform electrical field [J]., 2010, 27 (1): 198-205

[7] Ha Jong Wook, Yang Seung Man. Break up of a multiple emulsion drop in a uniform electric field [J]., 1999, 21 (3): 92-100

[8] Sun Zhiqian (孙治谦), Jin Youhai (金有海), Wang Lei (王磊), Wang Zhenbo (王振波). Impact of high-frequency pulse electric field parameters on polarization and deformation of water droplet [J].(化工学报), 2012, 63 (10): 3112-3118

[9] John S Eow, Mojtaba Ghadiri. Electrostatic enhancement of coalescence of water droplets in oil: a review of the technology [J]., 2002, 85: 357-368

[10] Feng J G, Scott T C. A computational analysis of electrohydrodynamics of a leaky dielectric drop in an electric field [J].. ,1996, 311: 289-326

[11] Lac E, Homsy G M. Axisymmetric deformation and stability of a viscous drop in a steady electric field [J].., 2007, 590: 239-264

[12] Wei Wei (危卫), Zhang Yunwei (张云伟), Gu Zhaolin (顾兆林). The electrorheological droplet’s deformation and mechanical beavior [J].(科学通报), 2013, 58 (3): 197-205

[13] Liang Meng (梁猛), Li Qing (李青), Wang Kuisheng (王奎升), Liu Jingye (刘竟业), Chen Jiaqing (陈家庆). Deformation and break of dispersed phase droplets in uniform electric field [J].(化工学报), 2014, 65 (3): 843-848

[14] Zhang Jun (张军), He Hongzhou (何宏舟). Dynamics of dispersed droplets in demulsification under high electrical voltage [J].(化工学报), 2013, 64 (6): 2050-2057

[15] Kazimierz Adamiak, Jerzy M Floryan. Dynamics of water droplet distortion and breakup in a uniform electric field [J]...., 2011, 47 (6): 2374-2382

[16] Zhang Jun (张军), He Hongzhou (何宏舟), Huang Guanxing (黄冠星). Simulation of droplet deformation in uniform electric field with dissipative particle dynamics approach [J].(化工学报), 2014, 65 (10): 3872-3877

[17] Bai Li (白莉), Ni Lingying (倪玲英), Guo Changhui (郭长会), Wei Qingcai (魏庆彩). Analysis of the droplets’ deformation and breakage in high voltage DC field [J].(应用力学学报), 2013, 30 (1):76-79

[18] Jacqmin D. Calculation of two-phase Navier-Stokes flows using Phase-Field modeling [J]., 1999, 155:96-127

[19] Taylor G I. The deformation of emulsions in definable fields of flow [J].... ,1934, 146: 501-523

[20] Yan Zhang (严璋), Zhu Deheng (朱德恒). High Voltage Insulation Technology (高电压绝缘技术) [M]. 2nd ed. Beijing: China Electric Power Press, 2009: 7-12

Kinetics behavior of water droplet deformation in emulsified oil subjected to non-uniform electric field

CHEN Qingguo1, SONG Chunhui1, LIANG Wen1, ZHENG Tianyu1, LIU Zeng2,ZHAO Zhongshan2, WEI Xinlao1

(Key Laboratory of Engineering Dielectrics and Its ApplicationMOEHarbin University of Science and TechnologyHarbinHeilongjiangChina;Design Institute of Daqing OilfieldDaqingHeilongjiangChina

Kinetics behavior of droplet deformation under electric field is important in the research on emulsion electric dehydration mechanism. In order to study the dynamic behavior of water droplets under non-uniform electric field, a simulation model of droplet under non-uniform electric field was established through the phase field method based on Cahn-Hilliard formulation. The distributions of charge density and electric field force on the droplet surface as well as the coupling effect of flow field and electric field were investigated during the process of droplet deformation, moving and coalescence. The influences of droplet size, electric field strength and non-uniform coefficient on droplet behavior were simulated and analyzed. The experimental study on the emulsion dehydration under non-uniform electric field was conducted by using the small dehydration test system in laboratory, and the droplets motion in the emulsion under different conditions was observed and analyzed by high-speed camera. The distribution of polarization charges was different on the droplet surface under non-uniform electric field, increasing from the center to both ends of the droplet. The values of polarization charge and Maxwell stress at droplet’s one end surface closed to electric field concentrated area were the largest. The increase of electric field strength, electric field non-uniformity coefficient or droplet diameter could lead to larger droplet deformation, faster moving of droplet to concentrated electric field area, and higher coalescence rate.

non-uniform electric field; phase field method; deformation; kinetics; coalescence; numerical simulation

2014-10-23.

SONG Chunhui, songchunhui0903@163.com

10.11949/j.issn.0438-1157.20141600

TE 624

A

0438—1157（2015）03—0955—10

国家重点基础研究发展计划项目（2012CB723308）；黑龙江省科技攻关项目（GZ11A210）。

2014-10-23收到初稿，2014-11-28收到修改稿。

联系人：宋春辉。第一作者：陈庆国（1970—），男，博士，教授。

supported by the National Basic Research Program of China (2012CB723308) and the Key Science and Technology Program of Heilongjiang Province (GZ11A210).