二流—四流球谐函数谱展开累加辐射传输方案在全球气候模式中的应用
2015-10-14张华卢鹏荆现文
张华 卢鹏 荆现文
二流—四流球谐函数谱展开累加辐射传输方案在全球气候模式中的应用
张华1, 2卢鹏3, 1荆现文1, 2
1中国气象局气候研究开放实验室/国家气候中心,北京100081;2南京信息工程大学气象灾害预报预警与评估协同创新中心,南京210044;3江苏省气候中心,南京210008
本文首先构建了二流—四流球谐函数谱展开累加辐射传输的新方案,然后将其应用于国家气候中心第二代大气环流模式BCC_AGCM2.0.1的新版本中,并与模式中原有的Eddington累加方案进行了比较。由于新方案本质上是单层Eddington近似方案在四流上的推广。因此新方案在计算精度上要优于原方案。通过在全球气候模式中的应用与比较,本文发现新方案对气候模拟会产生比较大的影响。在晴空条件下,新方案计算的在南纬30°到60°区间、北大西洋东北部以及非洲北部的撒哈拉沙漠区域的地表向下年平均短波辐射通量要小于原方案结果,最大差别可以达到3.5 W/m2;同时,新方案计算的在南纬30°到60°区间和北大西洋东北部的大气顶向上年平均短波辐射通量要大于原方案结果,最大差别达到3 W/m2。在有云大气情况下,新方案计算的地表向下年平均短波辐射通量要小于原方案结果,并随着纬度的增加,新旧两种方案的差别逐渐变大,在南北极时达到最大5.5 W/m2;同时,新方案计算的在赤道区域的大气顶的年平均短波向上辐射通量要小于原方案结果,最大差别为2.5 W/m2,而在南北纬30°到60°区间,新方案计算的在大气顶的年平均短波向上辐射通量则要大于原方案结果,最大差别为1.5 W/m2。新方案计算的年平均短波加热率普遍高于原方案结果,特别是在800 hPa到地表之间的低层大气以及50 hPa到100 hPa的高层大气,最大差别可达0.03 K/d。因此,新方案有助于改善全球气候模式中普遍存在的赤道平流层中下层的温度冷偏差现象。
四流球谐函数 辐射传输方案 辐射通量 加热率 冷偏差
1 引言
辐射过程是大气中最重要的物理过程之一。一方面,地气系统的辐射收支决定了长期的全球平均气候状况;另一方面,太阳辐射能和热辐射能在大气中的辐散、辐合,形成非绝热冷、热源,造成大气水平和垂直层结的不稳定(石广玉,2007)。在具体的大气辐射模式中,前者通过大气顶和地表的辐射通量表征;后者通过大气加热率反映。
气候模式中的辐射模式比较计划(简称:ICRCCM,the Intercomparison of Radiation Codes in Climate Models)第一阶段第二部分(Fouquart et al., 1991)比较了26个短波辐射模式。其中在晴空条件下共有21个大气辐射模式参加了比较(不包括逐线积分模式),结果表明:各模式间的均方根差 别在4%左右。在有云大气条件下,均方根的差 别随着云层光学厚度的变化而变化,从4%到10%。ICRCCM第三阶段(Barker et al., 2003)比较了25个短波辐射模式,其中包括2个逐线积分模式、4个蒙特卡洛光子输运算法。在热带大气廓线条件下,在太阳直射时,无论有云与否,大多数短波辐射模式都会低估15~25 W/m2的大气吸收。Halthore et al.(2005)评估了16个短波辐射模式,结果表明,在晴空不考虑气溶胶大气情况下,各种短波辐射模式计算的地表直接辐射强度之间的均方根方差在1%以内,但在湿大气情况下,均方根方差达到5%左右。从上述比较可以看出,各种短波辐射算法很难达到一致,短波辐射模式的精度还需要进一步的提高。
目前大多数气候模式仍然采用二流近似辐射传输方案。该方案的优点在于计算速度快,但是与四流近似辐射传输方案相比,该方案在有云大气的情况下的计算误差比较大。在美国标准大气廓线情况下,二流近似辐射传输方案与48流DISORT离散纵坐标的参考结果相比,云顶加热率有可能被低估约6%(Zhang et al., 2013;Zhang and Li, 2013)。
Shibata and Uchiyama(1992)评估了四流矩阵算子法,当太阳天顶角小于72.5°时,相对误差小于5%;当太阳天顶角大于72.5°时,相对误差小于10%。Chou(1992)利用单层四流离散坐标法结合累加法计算辐射通量和加热率,与传统的通过求解线性方程组的四流离散坐标法相比,明显地节省了计算时间,因此可以应用于气候模式中。Kay et al. (2001)分别评估了二流和四流离散纵坐标法以及矩阵求逆法,结果表明在光化通量的计算中,四流离散纵坐标法略优于矩阵求逆法,而两者都要优于二流离散纵坐标法。而在辐射通量的比较中,四流离散纵坐标法要优于矩阵求逆法和二流离散纵坐标法。Ayash et al.(2008)在第三代加拿大气候中心大气环流模式(Scinocca et al., 2008)(简称:CCC GCM3,the third-generation Canadian Climate Center Atmosphere GCM)中评估了二流—四流混合离散纵坐标法(Liou et al., 1988)与二流近似辐射传输算法对辐射通量的影响。Liu et al.(2009)将Fu-Liou四流离散纵坐标辐射传输算法加入美国海军海气耦合中尺度预报系统(简称:COAMPS,Coupled Ocean–Atmosphere Mesoscale Prediction System)中,发现对三天短期天气预报的温度场有很大的改进。
Li and Ramaswamy(1996)通过比较表明,对于求解单层辐射传输方程而言,四流球谐函数辐射传输方法的透过率和反射率的精度都要略高于四流离散纵坐标方法的结果。本文利用单层四流球谐函数谱展开代替原有的二流近似解来计算均匀的单层介质的的透射率和反射率,其采用的累加过程还是原有的二流累加法(Coakley et al., 1983)。这种单层四流球谐函数谱展开和二流近似累加法结合的方法,即为二流—四流球谐函数谱展开累加法(下文中简称:新方案)。
本文将以上新方案应用到国家气候中心气候模式BCC_AGCM2.0.1新的版本(荆现文和张华,2012;Zhang et al., 2014)中进行检验和评估,以改进该模式对大气辐射的计算精度。
本文的第二部分给出了在非均匀多层大气中四流球谐函数辐射传输方案的构建;第三部分简要介绍了所用的全球气候模式和数值检验方法;第四部分比较分析了新方案与Eddington近似方案在气候模式中的表现及其模拟差异;最后在第五部分给出了本文的主要结论。
2 四流球谐函数辐射传输方案构建
辐射传输方程可以写成以下形式:

其中,为局地天顶角,是辐射强度,是光学厚度,是多次散射项,0是单次散射项。四流球谐函数辐射传输算法将辐射强度展开成球谐函数如下:

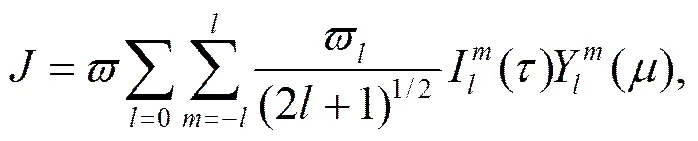
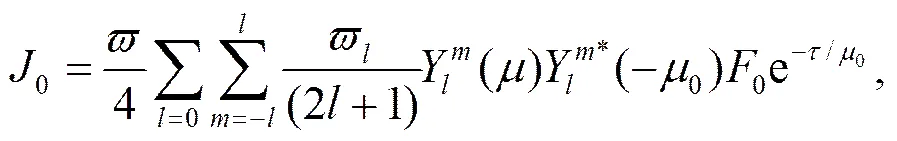
将(2),(3),(4)式代入(1)整理,并将展开到第4项,可得常系数线性微分方程组。通过求解可得辐射强度的各展开项的数值。利用公式(2)可得到辐射强度,同时也可以得到透过率和反射率。详细的推导过程也可见Li and Ramaswamy(1996)及Zhang and Li(2013)。
在求解方程时如果不考虑直接入射项,则可以通过求解齐次常系数线性微分方程组得到漫射的透过率和反射率。对于两层总的透过率和反射率则可通过Coakley et al.(1983)的公式求得:




通过上述公式(5)到(8),可以得到任意2层的反射率和透过率,从而得到非均匀大气每层的向上通量和向下通量。
本文在Li and Ramaswamy(1996)基础上,在数值上实现了二流—四流球谐函数谱展开累加计算,并将之应用于全球气候模式中进行比较和评估。
3 全球气候模式介绍和数值检验方法
本文采用国家气候中心第二代大气环流模式BCC_AGCM2.0.1(Wu et al., 2008,2010)的新版本。其水平分辨率为T42(近似于2.8度乘以2.8度),垂直方向采用混合坐标,共26层。新版本的重要特征是更新了BCC_AGCM2.0.1的辐射过程和云的垂直重叠处理,新的辐射过程采用Zhang et al.(2003,2006a,2006b)发展的BCC-RAD辐射模块(Randles et al., 2013;Zhang et al., 2014)。云的垂直重叠采用McICA蒙特卡洛随机次网格柱方法处理(荆现文和张华,2012;Jing and Zhang,2013)。气溶胶过程采用Gonget al.(2002,2003)开发的CUACE_Aero气溶胶理化数值模式(Zhang et al., 2012)。Wuet al.(2010)对BCC_AGCM2.0.1模式的模拟性能进行了系统的评估。
BCC-RAD辐射模块对于气体吸收采用相关分布算法(Shi,1981;张华,1999);对于辐射传输方程的求解,本文采用了Eddington二流累加法和二流—四流球谐函数谱展开累加两种辐射传输算法来计算大气辐射通量和加热/冷却率。
本文通过离线诊断和在线模拟两种方式比较Eddington近似和本文提出的新算法在气候模式中的模拟效果。离线诊断是在运行Eddington二流辐射传输算法的同时,加入新方案,但新方案的输出量仅作为诊断量,不产生气候反馈。离线诊断主要用于检验在相同大气条件下辐射传输算法本身的差别。在线模拟是在相同的初始场条件下分别运行Eddington近似和新方案,以检验两种方法各自对气候模拟的影响。首先离线诊断了两种方法的辐射场差异,重点给出了地表向下的短波辐射通量、大气顶向上短波辐射通量和短波辐射加热率的结果,它们分别反映了以上不同辐射传输算法下大气的透射率、反射率和大气加热情况。然后给出了两种方法对气候模拟的影响,重点分析了两种辐射传输算法对云辐射强迫的影响。
离线诊断和在线运行都是从1949年9月1日开始,积分52个月。其中辐射方案每小时调用一次(模式的积分步长为20分钟,也就是3个模式积分步长调用一次)。前16个月为Spin-up时间,取后三年(1951~1953年)的结果进行分析。所用海温资料为多年平均的月平均气候态数据(Hurrell and Trenberth, 1999)。
4 结果分析
4.1 晴空辐射通量
图1a、b分别给出了两种辐射传输算法得到 的晴空条件下地表向下和大气顶向上年平均短波辐射通量差异。从图1a可以看出,两种方案在晴空大气条件下地表向下短波辐射通量的差别较大的区域主要发生在南纬30°到60°区间的海洋表面以及非洲北部的撒哈拉沙漠,分别处于海盐气溶胶和沙尘气溶胶含量较高的区域,这些区域Eddington近似方法都高估了地表向下的短波辐射通量。Li and Ramaswamy(1996)的结果表明二流近似与新方案相比,不论是粒子单次散射比为1还是0.9都高估了大气的透射率,因此,在气溶胶浓度高的区域,Eddington近似会高估对晴空地表向下的辐射通量。
从图1b可以看出,Eddington近似与新方案相比,对大气顶向上短波辐射通量的最大低估区主要位于南北纬30°到60°的海洋区域,但在非洲北部的撒哈拉沙漠却仅出现微弱的低估和高估。Li and Ramaswamy(1996)表明:与Eddington近似相比,不论是单次散射比为1还是0.9,新方案的反射率在太阳天顶角余弦比较大时存在高估,而在太阳天顶角比较小时存在低估。而在南北纬30°到60°的海洋区域正好对应太阳天顶角余弦值比较小的时候,因此大气顶的向上通量会被低估;而对于撒哈拉沙漠区域,当太阳在北半球时则对应太阳天顶角余弦值比较大的情况,当太阳在南半球时则对应太阳天顶角余弦值比较小的情况,因此年平均的通量值正好被这种高估和低估相互抵消,仅出现很微弱的低估和高估。
4.2 有云大气辐射通量
图2与图1相似,但是为有云条件的相应结果。从图2a中可以看出,两种方案在有云大气条件下地表向下短波辐射通量的差值从赤道向两极逐渐变大,南北两极的差别最大。由于Eddington近似与新方案相比,整体都是高估单层透过率(Li and Ramaswamy,1996),同时在相同光学厚度条件下,两种算法计算的透过率差别随着太阳天顶角的增大而增大。而太阳天顶角随着纬度的增加而增加,正好与有云情况下地表向下短波辐射通量差值的分布相符。Ayash et al.(2008)的结果也表明,在有云大气情况下,二流辐射传输算法与二流—四流离散纵坐标累加算法相比到达地面的辐射通量偏多,特别是在高纬地区。
图2b表明两种方案在有云大气条件下大气顶向上短波辐射通量在热带区域存在正的差别,在南北半球中高纬度的海洋区域存在负的差别。这两个区域分别对应对流云量和层云量出现比较大的区域,云的光学厚度较大。由于当太阳天顶角余弦较大的时候,Eddington二流近似算法在反射率上存在高估,而在太阳天顶角余弦值较小的时候,Eddington二流近似算法在反射率上存在低估(Li and Ramaswamy,1996),因此在高纬度区域,对应太阳天顶角余弦值较小的情况,二流近似算法相对新方案低估了有云大气的大气顶向上短波辐射;在热带区域,对应太阳天顶角余弦值较大的情况,二流近似算法相对新方案高估了有云大气的大气顶向上短波辐射。Ayash et al.(2008)比较了二流近似与二流—四流离散纵坐标法也得到了相同的结果。

图1 用Eddington近似与新方案计算的晴空年平均辐射通量(W/m2)差值的全球分布(Eddington近似减去新方案):(a)地表向下短波辐射通量;(b)大气顶向上短波辐射通量

图2 同图1,但为有云大气条件
4.3 短波加热率
图3给出了Eddington方法与新方案计算的年平均短波加热率的差别的纬度—高度分布。可以看出,两种方法造成的短波加热率差异主要发生在800 hPa到地表的低层大气以及50 hPa到100 hPa的高层大气。对800 hPa到地表的区域,偏差最大超过0.2 K/d,这主要是受低云的影响。对于100 hPa以上的区域,Eddington近似方案相对新方案,加热率也有一个负偏差。在100 hPa以上的区域,主要处于平流层,目前全球气候模式对温度场的模拟在热带上空的平流层中下层区域几乎都存在一个冷偏差,这是全世界气候模拟普遍存在的问题(Forster et al., 2011),而Eddington近似和新方案计算的加热率差值表明,在该区域如果采用新方案计算,将会比Eddington近似计算的加热率强,有助于改善气候模式的冷偏差问题。

图3 用Eddington方法与新方案计算的年平均短波加热率差值(K/d)的纬度—高度分布(前者减去后者)
图4给出Eddington近似方法、新方案与ECMWF资料温度差值的纬度—高度分布图。从图4可以发现,采用新方案计算的温度场结果在50~100 hPa赤道地区的的确要优于Eddington近似方案,对原有模式中热带上空平流层的冷偏差有所改进。而该区域大气成分的分布及变化对于认识气候长期变化极为重要,因为该区域的臭氧、水汽、卷云和气溶胶对太阳短波辐射和地球长波辐射有很强的调节作用(陈洪滨等,2006)。
4.4 云辐射强迫
图5给出Eddington近似方法和新方案模拟的短波区间云辐射强迫与CERES资料的差值图,可以看出Eddington近似与CERES资料的全球平均值相比低估了―1.32 W/m2, 新方案与CERES资料的全球平均值相比低估了―0.33 W/m2。原因可能是由于新方案计算的加热率要大于Eddington近似方案,尤其是在加热率最大的云顶处,因此云顶的加热率变大,将抑制云的发展从而减少云量,从而减少反射到大气顶的辐射通量,使得短波区间云的负辐射强迫变小、云辐射强迫与CERES资料的结果更加接近。

图4 Eddington近似和新方案与ECMWF资料温度场差值的纬度—高度分布:(a)Eddington近似方法与ECMWF资料的差值;(b)新方案与ECMWF资料的差值

图5 Eddington近似方法和新方案与CERES资料大气顶短波云辐射强迫的差值场:(a)Eddington近似方法与CERES资料的差值(a)新方案与CERES资料的差值
从全球分布来看,新方案与Eddington近似方法相比,在北太平洋中部和南纬45°到60°海域,对模式模拟的短波云顶辐射强迫的误差有所减少。丁守国等(2005)利用ISCCP月平均云气候资料研究了全球云量分布,从年平均的经向平均图来看,云量的分布有三个峰值带,分别位于北纬10°,和南北纬60°附近,云量都在70%以上。而新方案与Eddington方法相比,改善最大的地方也是在北纬10°和南纬60°附近,表明,本文提出的新方案在云量较多的地方对模式模拟的短波大气顶云辐射强迫有较大改进。
5 主要结论
本文利用单层四流球谐函数谱展开算法结合二流累加法,构造了一种精度介于二流辐射方案和四流矩阵求解法之间的二流—四流球谐函数谱展开累加辐射传输算法。并将其应用于中国气象局国家气候中心的全球气候模式BCC_AGCM2.0.1的新版本中(荆现文和张华,2012;Zhang et al., 2014),检验了本文构建的新方案的模拟效果并与原方案进行了比较。得到的主要结论如下:
(1)在晴空情况下,Eddington近似方案和本文提出的新方案在大气顶和地表的辐射通量差异主要是由气溶胶引起的。其中对于晴空短波地表向下辐射通量,海盐气溶胶和沙尘气溶胶分别是造成Eddington近似方案和新方案差异的主要来源。对于晴空短波大气顶向上辐射通量,海盐气溶胶是造成这种差异的主要来源。
(2)在有云大气情况下,Eddington近似方案和新方案在大气顶和地表的辐射通量差异主要是由于太阳天顶角决定的。对于有云大气短波地表向下辐射通量而言,Eddington近似方案和新方案的差值从赤道向两极逐渐变大,南北两极的差别最大。对于有云大气大气顶短波向上辐射通量,Eddington近似方案与新方案相比,在高纬度地区低估了大气顶短波向上辐射通量,而在热带地区高估了大气顶短波向上辐射通量。
(3)对于短波加热率而言,新方案的加热率普遍要强于Eddington近似方案,尤其在800 hPa到地面区域和50 hPa到100 hPa区域。其中800 hPa下方的加热率,差异在云顶最大,因此会抑制云的生成,从而增加云的短波辐射通量;而100 hPa上方的正加热偏差则有助于改善在大多数模式中普遍存在的赤道平流层中下层的冷偏差现象。
此外,本文提出的新方案与二流累加辐射传输方案相比的最大优势是显著提高了对单层反射率和透过率的模拟精度。当然本文构造的新方案也有一定的局限性,单层的四流球谐函数方法可以用来计算各个方向的辐射强度,但受限于二流累加法,必须将各个方向的辐射强度积分到向上和向下两个方向的辐射通量。在这个过程中将损失部分精度,因此下一步工作我们期望将新研制的四流球谐函数辐射传输累加法(Zhang and Li,2013)应用 于本文的全球气候模式中并对模拟精度和计算效率进行对比研究。
(References:)
Ayash T, Gong S L, Jia C Q. 2008. Implementing the delta-four-stream approximation for solar radiation computations in an atmosphere general circulation model [J]. J. Atmos. Sci., 65 (7): 2448–2457.
Barker H W, Stephens G L, Partain P T, et al. 2003. Assessing 1D atmospheric solar radiative transfer models: Interpretation and handling of unresolved clouds [J]. J. Climate, 16 (16): 2676–2699.
陈洪滨, 卞建春, 吕达仁. 2006. 上对流层—下平流层交换过程研究的进展与展望 [J]. 大气科学, 30 (5): 813–820. Chen H B, Bian J C, Lü D R. 2006. Advances and prospects in the study of stratosphere exchange [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 30(5): 813–820.
Chou M D. 1992. A solar radiation model for use in climate studies [J]. J. Atmos. Sci., 49 (9): 762–772.
Coakley J A Jr, Cess R D, Yurevich F B. 1983. The effect of tropospheric aerosols on the Earth’s radiation budget: A parameterization for climate models [J]. J. Atmos. Sci., 40 (1): 116–138.
丁守国, 赵春生, 石广玉, 等. 2005. 近20年全球总云量变化趋势分析 [J]. 应用气象学报, 16 (5): 670–677. Ding S G, Zhao C S, Shi G Y, et al. 2005. Analysis of global total cloud amount variation over the past 20 years [J]. Journal of Applied Meteorological Science (in Chinese), 16(5): 670–677.
Forster P M, Fomichev V I, Rozanov E, et al. 2011. Evaluation of radiation scheme performance within chemistry climate models [J]. J. Geophys. Res., 116 (D10): 10302, doi:10.1029/2010JD015361.
Fouquart Y, Bonnel B, Ramaswamy V. 1991. Intercomparing shortwave radiation codes for climate studies [J]. J. Geophys. Res., 96 (D5): 8955– 8968.
Gong S L, Barrie L A, Lazare M. 2002. Canadian Aerosol Module (CAM): A size-segregated simulation of atmospheric aerosol processes for climate and air quality models 2. Global sea-salt aerosol and its budgets [J]. J. Geophys. Res., 107 (D24): AAC 13-1–AAC 13-14, doi:10.1029/ 2001JD002004.
Gong S L, Barrie L A, Blanchet J P, et al. 2003. Canadian Aerosol Module: A size-segregated simulation of atmospheric aerosol processes for climate and air quality models 1. Module development [J]. J. Geophys. Res., 108 (D1): AAC 3-1–AAC 3-16, doi:10.1029/2001JD002002.
Halthore R N, Crisp D, Schwartz S E, et al. 2005. Intercomparison of shortwave radiative transfer codes and measurements [J]. J. Geophys. Res., 110(D11): D11206, doi:10.1029/2004JD005293.
Hurrell J W, and Trenberth K E. 1999. Global sea surface temperature analyses: multiple problemsand their implications for climate analysis, modeling, and reanalysis [J] Bull. Amer. Met. Soc., 80 (12):2661−2678
荆现文, 张华. 2012. McICA云—辐射方案在国家气候中心全球气候模式中的应用与评估 [J]. 大气科学, 36 (5): 945–958. Jing X W, Zhang H. 2012. Application and evaluation of McICA Cloud-Radiation framework in the AGCM of the National Climate Center [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 36(5): 945–958.
Jing X W, and Zhang H. 2013. Application and evaluation of McICA scheme in BCC_AGCM2.0.1 [C]. AIP Conf. Proc. 1531, 756, doi:10.1063/1.4804880.
Kay M J, Box M A, Trautmann T, et al. 2001. Actinic flux and net flux calculations in radiative transfer—A comparative study of computational efficiency [J]. J. Atmos. Sci., 58 (24): 3752–3761.
Li J, Ramaswamy V. 1996. Four-stream spherical harmonic expansion approximation for solar radiative transfer [J]. J. Atmos. Sci., 53 (8): 1174–1186.
Liou K N, Fu Q, Ackerman T P. 1988. A simple formulation of the delta-four-stream approximation for radiative transfer paramterization [J]. J. Atmos. Sci., 45 (13): 1940–1947.
Liu M, Nachamkin J E, Westphal D L. 2009. On the improvement of COAMPS weather forecasts using an advanced radiative transfer model [J]. Wea. Forecasting, 24 (1): 286–306.
Randles C A, Kinne S, Myhre G, et al. 2013. Intercomparison of shortwave radiative transfer schemes in global aerosol modeling: Results from the AeroCom Radiative Transfer Experiment [J]. Atmos. Chem. Phys., 13: 2347–2379.
Scinocca J F, McFarlane N A, Lazare M, et al. 2008. Technical Note: The CCCma third generation AGCM and its extension into the middle atmosphere [J]. Atmos. Chem. Phys., 8, 7055–7074, doi:10.5194/ acp-8–7055-2008.
Shibata K, Uchiyama A. 1992. Accuracy of the delta-four-stream approximation in inhomogeneous scattering atmospheres [J]. J. Meteor. Soc. Japan, 70 (6): 1097–1109.
Shi G Y, 1981. An accurate calculation and representation of the infrared transmission function of the atmospheric constituents [D]. Ph.D. dissertation, Dept. of Science, Tohoku University of Japan, 71pp.
石广玉. 2007. 大气辐射学[M]. 北京: 科学出版社, 1. Shi Guangyu. 2007. Atmospheric Radiation (in Chinese) [M]. Beijing: Science Press, 1.
Wu T W, Yu R C, Zhang F. 2008. A modified dynamic framework for the atmospheric spectral model and its application [J]. J. Atmos. Sci., 65 (7): 2235–2253.
Wu T W, Yu R C, Zhang F, et al. 2010. The Beijing Climate Center atmospheric general circulation model: Description and its performance for the present-day [J]. Climate Dyn., 34 (1): 123–147.
Zhang F, Li J. 2013. Doubling-adding method for delta-four-tream spherical harmonic expansion approximation in radiative transfer parameterization [J]. J. Atmos. Sci., 70: 3084–3101.
Zhang F, Shen Z P, Li J N, et al. 2013. Analytical delta-four-stream doubling–adding method for radiative transfer parameterizations [J]. J. Atmos. Sci., 70 (3): 794–808.
张华. 1999. 非均匀路径相关-分布方法的研究 [D]. 中国科学院大气物理研究所博士学位论文, 169pp. Zhang Hua. 1999. On the study of a new correlated-distribution method for nongray gaseous absorption in the inhomogeneous scattering atmosphere [D]. Ph. D. dissertation (in Chinese), Institute of Atmospheric Physics, Chinese Academy of Sciences, 169pp.
Zhang H, Nakajima T, Shi G Y, et al. 2003. An optimal approach to overlapping bands with correlateddistribution method and its application to radiative calculations [J]. J. Geophys. Res., 108(D20): 4641, doi:10.1029/2002JD003358.
Zhang H, Shi G Y, Nakajima T, et al. 2006a. The effects of the choice of the-interval number on radiative calculations [J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 98 (1): 31–43.
Zhang H, Suzuki T, Nakajima T, et al. 2006b. Effects of band division on radiative calculations [J]. Optical Engineering, 45 (1): 016002.
Zhang H, Wang Z L, Wang Z Z, et al. 2012. Simulation of direct radiative forcing of aerosols and their effects on East Asia climate using an interactive GCM–aerosol coupled system [J]. Climate Dyn., 38 (7): 1675–1693.
Zhang H, Jing X W, Li J N. 2014. Application and evaluation of a new radiation code under McICA scheme in BCC_AGCM2.0.1 [J]. Geosci. Model Dev., 7: 737–754.
张华, 卢鹏, 荆现文. 2015. 二流—四流球谐函数谱展开累加辐射传输方案在全球气候模式中的应用[J]. 大气科学, 39 (1): 137−144, doi:10.3878/j.issn. 1006-9895.1404.13316. Zhang Hua, Lu Peng, Jing Xianwen. 2015. Application of two-four stream spherical harmonic expansion approximation in a global climate model [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 39 (1): 137−144.
Application of Two−Four Stream Spherical Harmonic Expansion Approximation in a Global Climate Model
Zhang Hua1, 2, LU Peng3, 1, and Jing Xianwen1, 2
1,,,100081;2,,210044;3,210008
In this study, a new scheme for the radiative transfer algorithm, calledthe two−four stream spherical harmonic expansion approximation, is built and applied in the new version of the Beijing Climate Center atmospheric general circulation model (BCC_AGCM2.0.1). It is then compared with the original Eddington approximation scheme. Because this new scheme expands the Eddington approximation to solve radiative transfer through the atmosphere, it has better accuracy. We found the new scheme to have a great effect on climatic simulation. In a clear sky, the new scheme reduces the shortwave downward radiative flux in the surface in the 30°–60°S regions, in the Northeast Atlantic, and in the Sahara desert, with the largest reduction being 3.5 W/m2. Meanwhile, it increases the shortwave upward radiative flux at the top of the atmosphere (TOA) in the 30–60°S regions and in the Northeast Atlantic, with the largest increase being 3 W/m2. For all-sky cases, the new scheme reduces the shortwave downward radiative flux, and the difference between the two schemes becomes larger with increasing latitude. The largest difference reaches 5.5 W/m2in the two polar regions. The new scheme also reduces the shortwave upward radiative flux at the TOA in the tropics, with the largest difference being 2.5 W/m2, but increases this flux in the 30°–60°S regions, with the largest difference being 1.5 W/m2. Moreover, the new scheme increases the shortwave heating rate within the atmosphere generally, especially for the levels between 800 hPa and the surface and between 50 and 100 hPa where the largest difference reaches 0.03 K/d. Therefore, the new scheme is useful in global climate modeling for improving the so-called temperature cold bias phenomena generally existing in the lower parts of the stratosphere above the tropics.
Four-stream spherical harmonic expansion, Radiative transfer, Radiative flux, Heating rate, Temperature cold bias
1006−9895(2015)01−0137−08
P422
A
10.3878/j.issn.1006-9895.1404.13316
2013−03−16;网络预出版日期2014−05−07
国家自然科学基金项目41375080,科技部公益性行业(气象)科研专项项目GYHY201406023,国家重点基础研究发展计划项目2011CB403405
张华,女,1965年出生,博士,研究员,主要从事气溶胶—云—辐射相互作用及其气候效应、大气辐射传输模式等方面的研究。E-mail: huazhang@cma.gov.cn
