基于对称天线相位干涉仪的入射角估计及跟踪

2015-10-14魏子翔胡永芳吴嗣亮

电子与信息学报 2015年10期

魏子翔胡永芳崔嵬吴嗣亮

魏子翔①胡永芳②崔嵬*①吴嗣亮①

①(北京理工大学信息与电子学院北京 100081)②(上海宇航系统工程研究所上海 201108)

针对现有相位干涉仪角度估计算法在近场条件下性能不佳的问题，该文提出一种远近场均性能良好的改进的导向矢量匹配算法。该算法采用对称结构天线接收来波信号，利用近场条件下对称位置天线的到达相位差中距离相关项对消的特性设计新的代价函数。代价函数最大值位置对应的入射角即为目标信号的入射角估计。在此基础上，利用相关函数的梯度正比于角度误差的特性设计角跟踪环路。作为一种局部极值估计算法，角跟踪环路相比其它全局最大值估计算法具有更好的相位噪声鲁棒性。仿真实验验证了该算法在不同相位噪声以及远近场条件下的优良性能。

信号处理；相位干涉仪；角跟踪环路；对称阵列；入射角估计

1 引言

上述提及的各个算法均基于远场模型，当目标距离较近时这些算法可能存在角度正确估计概率的下降以及估计精度的恶化甚至无法正确估计入射角的问题。与远场模型不同，近场模型采用菲涅耳近似来描述接收信号的到达相位。注意到近场模型条件下，对称位置的天线到达相位差由于二阶泰勒展开项对消后仍与距离无关。据此，本文提出了一种基于对称结构天线的改进导向矢量匹配算法。该算法将对称位置天线接收信号的到达相位差作为导向矢量的基本元素并通过共轭对称的方式扩展阵列孔径，在远近场条件下均可获得高精度的入射角估计。另外在航天测控等领域常采用相位干涉仪处理周期重复信号以获得目标的实时状态估计。若采用现有算法只对单个周期信号进行参数估计，则未能充分利用不同时刻目标轨迹间的相关性。为此本文利用相关函数的梯度正比于角度误差的特性提出了一种角度跟踪环路。角跟踪环路本质上为相关函数局部极值的估计算法，因而在其获得正确角度初值后其角度正确估计概率明显高于其它全局最大值的搜索算法，具有更好的相位噪声鲁棒性。仿真实验验证了该算法的优越性。

2 问题描述

对式(1)进行泰勒展开，则可将各个天线的入射波相位近似表达为

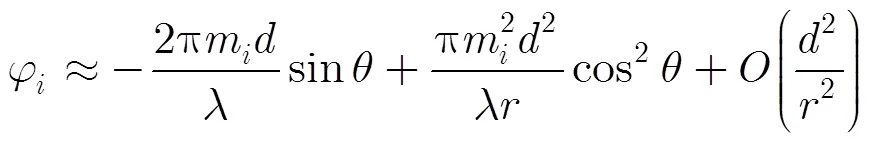
图1 对称结构的相位干涉仪示意图

3 基于对称阵列结构的相位干涉仪角度估计及跟踪算法

3.1改进的导向矢量匹配算法

导向矢量匹配算法采用远场模型估计入射角。当估计近场目标时，导向矢量匹配算法估计性能将显著恶化。为了实现良好性能的近场目标角度估计，本节将首先给出基于近场模型的导向矢量匹配算法。

将各天线的相位测量值重构为新的向量：

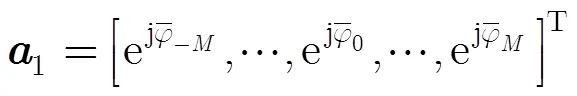
近场源条件下，对应的本地导向矢量为

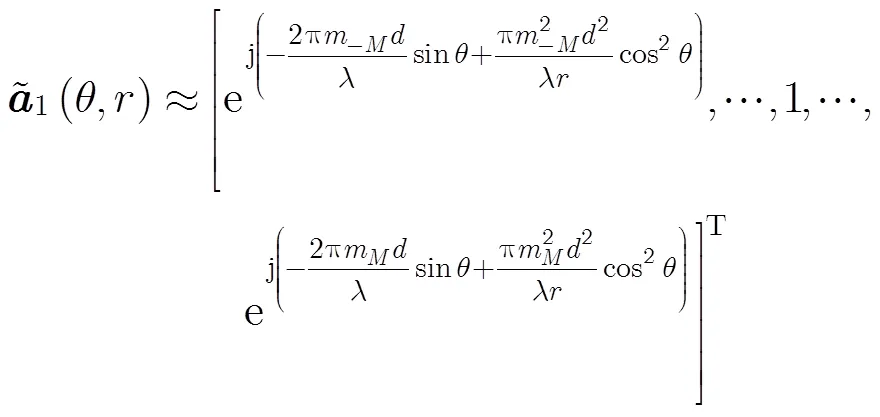
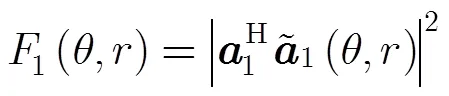
当存在测量相位噪声时，入射角估计为

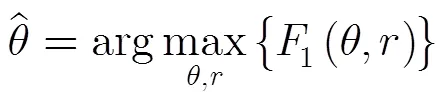
式(6)即为基于近场模型的导向矢量匹配算法。通过观察式(6)可以发现：近场条件下导向矢量匹配函数为以入射角和距离为变量的二元函数。入射角估计需通过对角度和距离的2维联合搜索实现，因而具有较高的计算复杂度。为此本节将提出一种改进的导向矢量匹配算法，该算法只需1维角度搜索即可获得近场条件下的目标信号入射角估计。

对于对称阵列而言，对称位置的阵元的相位差为

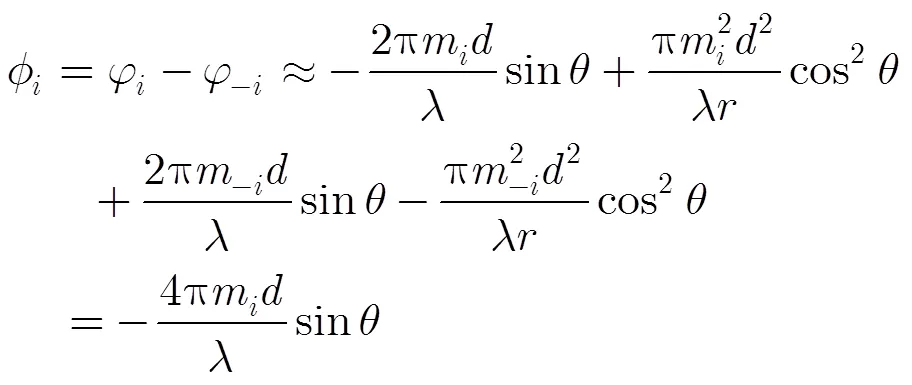
因而可利用式(7)，采用共轭对称的方法[15]将测量相位重构为

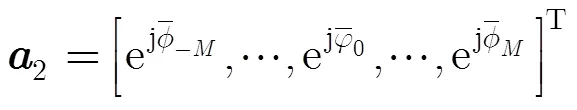
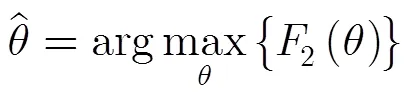
通过观察图2可以发现，原有的基于远场假设的导向矢量匹配算法的代价函数在目标由远场切换到近场后其幅度明显下降；改进的导向矢量匹配算法在远近场条件下幅值基本相同。由此可以看出，近场条件下原有的导向矢量匹配算法角度估计性能将恶化，而改进的导向矢量匹配算法角度估计性能不受影响。

3.2 闭环结构的角度跟踪算法

在航天测控、航天器交会对接以及卫星平台相互定位等领域常采用相位干涉仪处理重复周期已知的重复信号(如脉冲多普勒雷达发生的周期重复脉冲信号和连续波雷达发射的连续波信号等)而非突发信号，用以获得目标的实时位置估计。在这种情况下可以使用跟踪环路代替代价函数搜索方法可高性能且低代价获得入射角估计。本节将给出一种基于闭环结构的跟踪算法用于入射角快速测量。代价函数的梯度可以表达为

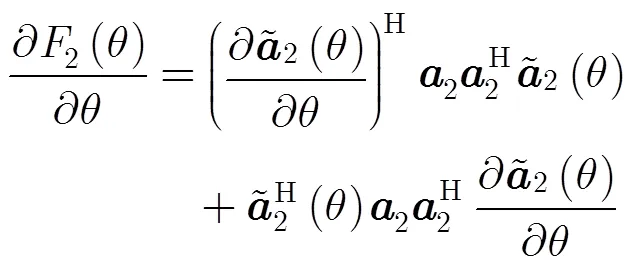
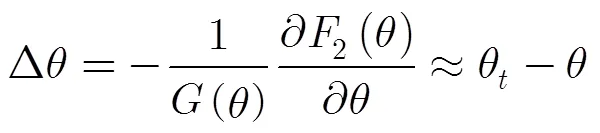
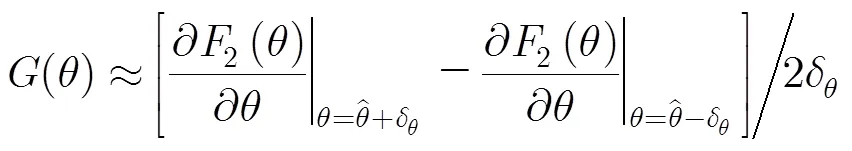
由式(13)得到角度误差估计后，可通过角度跟踪环路获得角度估计。与导航中常见的跟踪环路(如DDLL, FLL, PLL等)相似，角度跟踪环路将角度误差估计结果代入环路滤波器抑制噪声影响并经数控振荡器生成下一时刻的角度估计值。

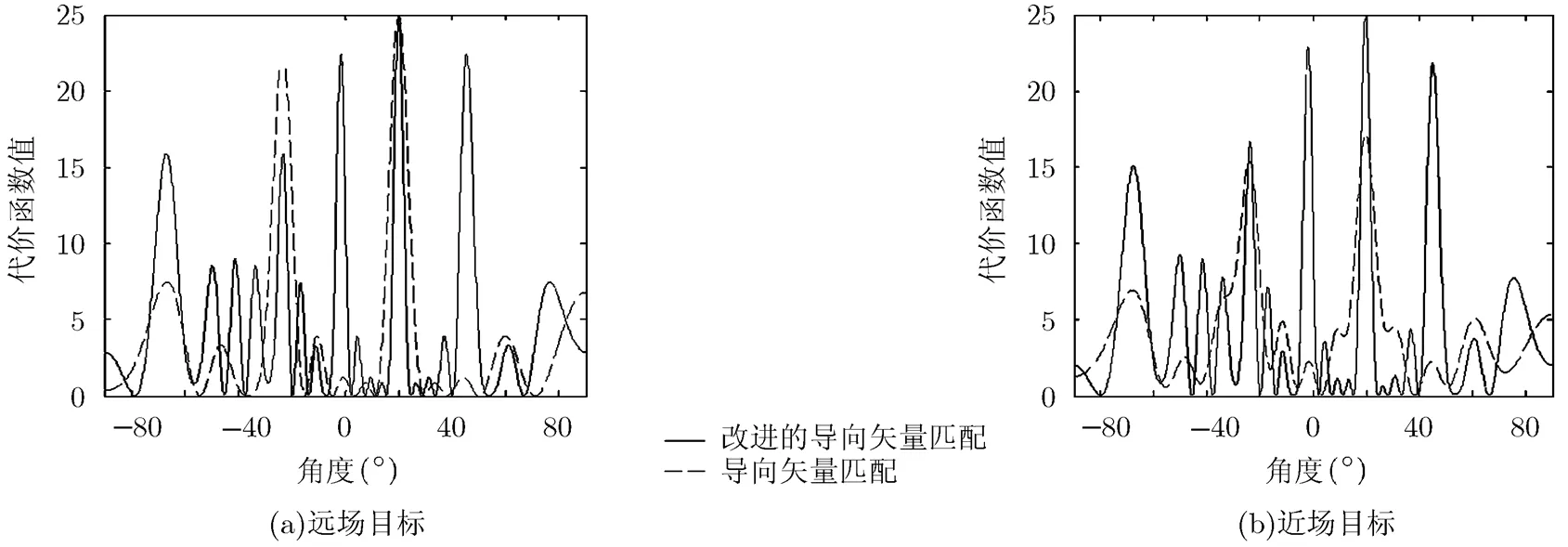
图2 两种算法的代价函数

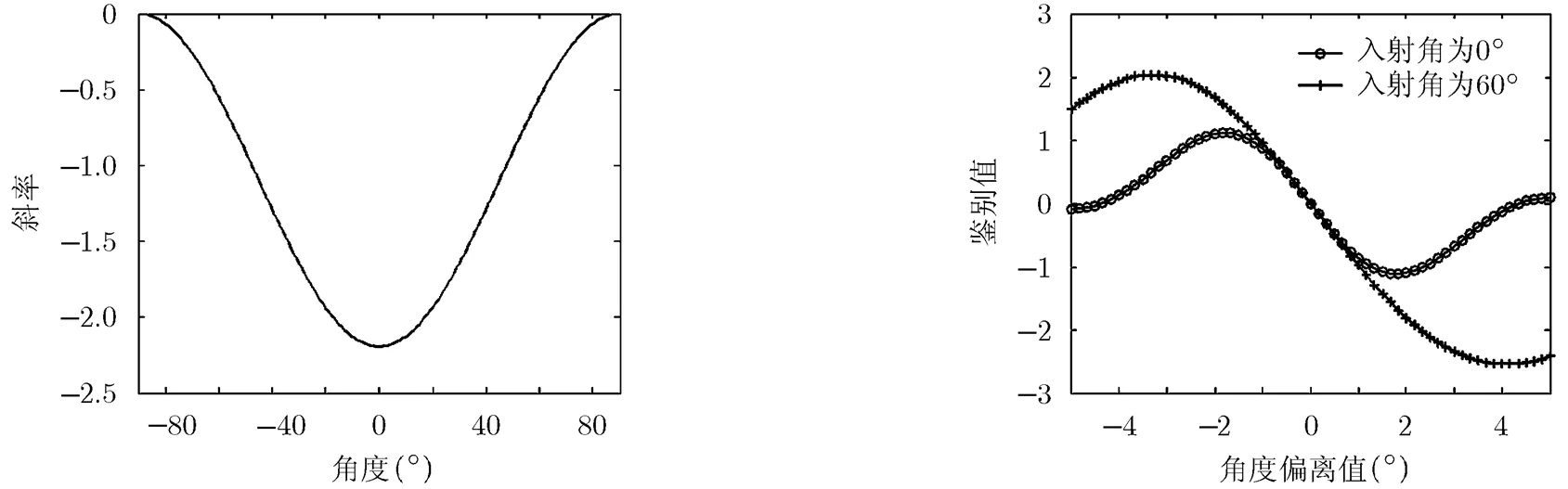
图3 不同入射角条件下梯度斜率图4 角度鉴别器鉴别曲线

如图5所示，角度跟踪环路由测量相位重构，本地信号导向矢量及其梯度矢量生成，梯度斜率估计，角度误差鉴别器，环路滤波器以及NCO几部分组成。角度误差鉴别器利用式(13)估计本地角度估计和真实角度之差，通过环路滤波器抑制噪声后经NCO累加获得更新的入射角度估计。通过对比式(10)和式(15)可以发现，角度跟踪环路无需角度搜索，算法实现需极低的运算代价。

4 仿真验证

由于角跟踪环路中采用环路滤波器抑制噪声，故当比较各算法角度估计精度性能时，亦对导向矢量匹配法、余弦函数匹配法、虚拟基线法以及基于RARE的算法角度估计结果采用滤波器抑制噪声。由式(15)可以得到角度跟踪环路的误差传递函数为

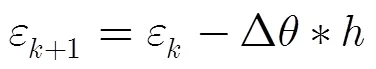
4.1角度正确估计概率

为了评估各算法远、近场条件下角度正确估计概率随信噪比的变化情况，考虑一个角速度为的匀速运动目标，目标的角度由到匀速变化。远场时目标的距离设定为，近场时目标的距离设为。采用角跟踪环路及其初始角度估计算法(即改进的导向矢量匹配算法)、导向矢量匹配算法、余弦函数匹配算法、虚拟基线法以及基于RARE的算法分别对500点数据进行入射角估计。角跟踪环路的初值估计、导向矢量匹配法以及余弦函数匹配法的角度搜索间隔均为；当各算法角度估计值偏离真实值小于时认为获得了正确的角度估计，统计角度正确估计概率如图6所示。

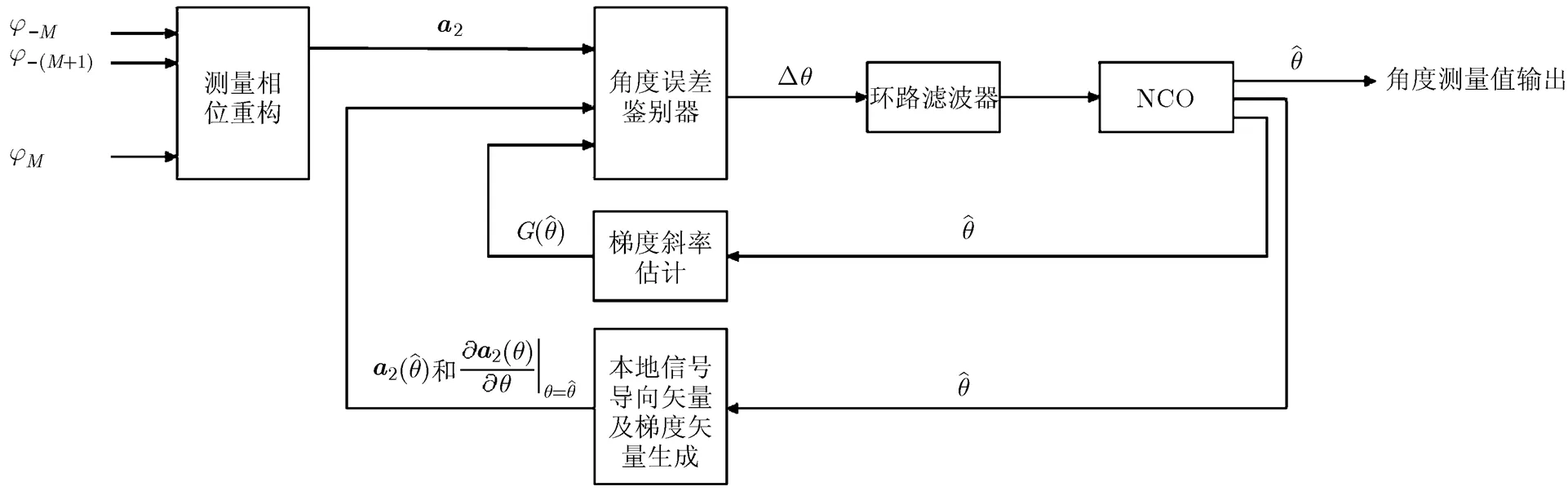
图5 角度跟踪环路结构框图

如图6所示，远近场条件下除角跟踪环路外，其它算法随着相位噪声的增加角度正确估计概率降低；角跟踪环路的正确估计概率一直保持为1，相比其它算法其具有更好的相位噪声鲁棒性；角跟踪环路角度初值估计算法和基于RARE的算法角度估计正确概率在远近场条件下均接近且优于虚拟基线法，3种算法的角度估计正确概率均不随远近场条件的变化而改变；导向矢量匹配算法和余弦函数匹配算法随着目标由远场切换到近场后，角度估计正确概率明显下降。远场条件下角跟踪环路的初值估计算法相比导向矢量匹配法和余弦函数匹配法其角度估计正确概率较低；然而由于角度初值估计算法只是应用于角度跟踪环路的初始角度估计过程中，因而可通过采用多点相位矢量平均[17]的方法来抑制相位噪声，从而提高其角度估计的正确概率。

图6 天线数目变化对参数估计性能影响

4.2角度估计精度

表1不同距离条件下各算法角度估计RMSE及正确概率(目标角度匀速变化)

从表1的统计结果可以看出，随着距离的减少，角跟踪环路、虚拟基线法以及基于RARE的算法的角度估计RMSE结果均无明显变化；余弦函数匹配法和导向矢量匹配法的RMSE结果分别在距离减小到和时显著恶化甚至无法正确进行角度估计。角跟踪环路在不同距离条件下均取得了优良的角度估计结果，角度估计精度与基于RARE算法相当，并优于其它3种算法。

4.3角度和距离同时变化时算法性能

4.1节和4.2节相关仿真验证了各算法在角度匀速运动、距离上静止条件下的性能。为了更加充分地评估各算法在动态条件下的性能，本节仿真将考虑一个在角度和距离同时做正弦运动的目标。目标在角度和距离上的运动过程如图7所示。相位测量值生成的时间间隔为0.1 s，相位噪声满足零均值高斯分布且其标准差为。采用角跟踪环路、导向矢量匹配法、余弦函数匹配法、虚拟基线法以及基于RARE的算法分别对500点数据估计目标角度。对各算法的角度估计结果的野值(角度估计值偏离真实值大于)进行处理(令其保持前一时刻数值)并将处理后的角度估计结果采用式(18)描述的滤波器抑制噪声影响。实施200次独立的蒙特卡罗仿真实验，统计各算法角度估计的正确概率及其均方根误差(RMSE)结果如图8所示。

由于各算法处理的数据长度较长(500点)，为了能够较清晰地在图中给出各个算法的统计数据，图8中的数据是在完成各算法的性能统计后对统计数据进行20倍抽取后的结果。

图8(a)中，3种近场源估计算法(包括角跟踪环路、虚拟基线法和基于RARE的算法)在随目标距离变化过程中，其角度估计正确概率无明显变化且均保持在较高水平(正确概率>0.9)，角跟踪环路和基于RARE的算法的角度估计正确概率优于虚拟基线法；而导向矢量匹配法和余弦函数匹配法在目标距离接近后，其角度估计正确概率均明显下降。图8(b)只给出了角跟踪环路、虚拟基线法和基于RARE的算法的仿真统计结果，这是由于导向矢量匹配法和余弦函数匹配法在近场条件下角度正确估计概率过低，难以统计其多次实验的均方根误差结果。从图8(b)中可以看出，当各算法收敛后(约1 s时刻后)，角跟踪环路和基于RARE的算法的角度估计RMSE性能接近且均优于虚拟基线法。这些结果也与4.1节和4.2节的相关仿真的结果一致。

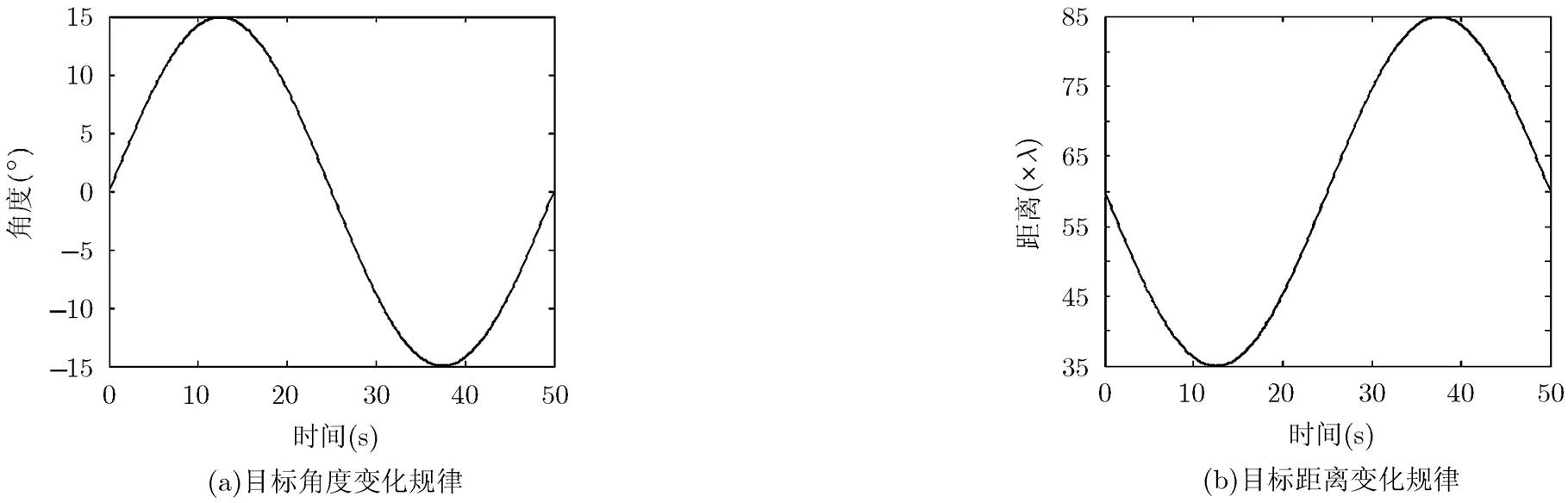
图7 目标运动规律

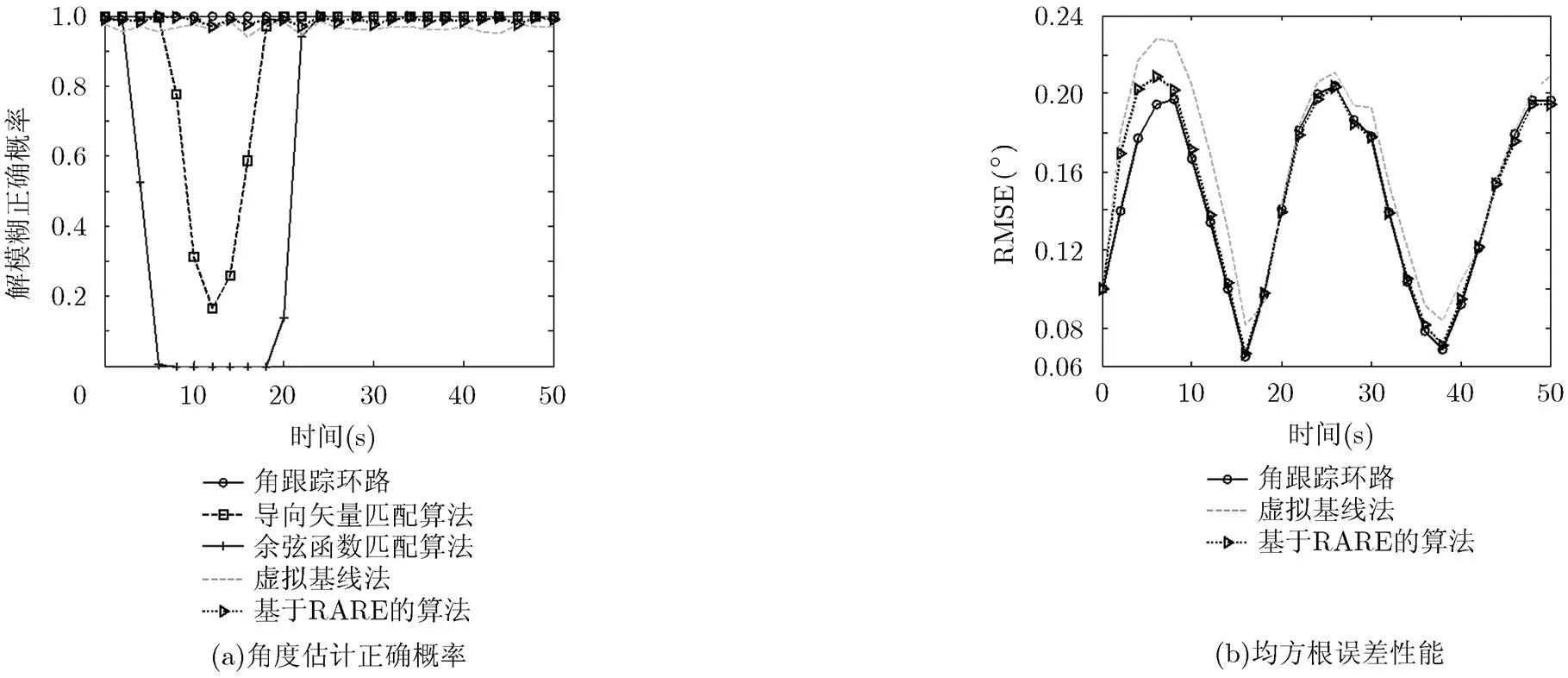
图8 各算法性能统计结果

4.4讨论

第1类相位干涉仪测角算法利用阵列的特殊几何关系来获得长基线相位差的整周模糊数估计。长基线相位差正确解模糊后，第1类算法仅采用单个基线的相位差转换获得入射角估计，因而其角度估计性能劣于充分利用各天线信息的第2类(即相关类)算法。不过这两类算法均基于远场模型提出，未对近场条件下的测角进行考虑。在近场条件下第1类算法若采用对称位置的相位差解相位差模糊并估计入射角则该类算法仍能正常工作；第2类算法由于采用本地信号与接收信号进行相关，在近场条件下若仍采用远场模型将会产生模型失配从而无法正确估计角度，若采用近场模型对算法进行修正则需要进行距离和角度的2维联合搜索，运算代价巨大。两类算法的优缺点如表2所示。

表2两类算法的优缺点

第1类算法第2类算法优点若采用对称位置的相位差来解相位差模糊则近场条件下仍能正常工作不易受到相位噪声影响缺点易受相位噪声影响近场条件下无法正常工作

本文提出的改进导向矢量匹配算法充分利用了各天线的有效信息，因而相比第1类算法不易受到相位噪声影响；由于利用了对称位置天线到达相位差的特点，因而近场条件下仍可正常获得角度估计。角度跟踪环路的提出进一步降低了改进导向矢量算法的运算代价且具有更好的相位噪声的鲁棒性：(1)角度跟踪环路通过估计并反馈角度估计误差的方式获得高精度的入射角估计，使得其无需角度搜索过程便可获得入射角估计；(2)角度跟踪环路本质上是一种局部极值的估计算法，因而对于稀疏阵列而言其角度估计正确概率显然优于现有的全局搜索算法。

除了以上传统的基于相位测量值的相位干涉仪信号处理算法，还有一些基于原始信号观测值的近场源估计算法可实现近场源入射角的高性能估计(如基于RARE的算法)。不过这些算法实现时往往需要协方差矩阵计算、矩阵的特征值分解和多次矩阵行列式或矩阵乘法的计算等操作，计算量方面远大于角跟踪环路，因而角跟踪环路不失为一种低代价且高性能的远近场通用的入射角估计方法，具有一定的实用价值。

5 结论

针对现有相位干涉仪测角算法难以获得近场源的高性能角度估计问题，本文提出一种改进的导向矢量匹配算法。该算法基于近场模型，利用对称位置天线的相位差不受距离影响的特性重构了阵列的导向矢量并获得以角度为变量的一元代价函数。通过搜索代价函数的最大值的方式获得入射角估计。利用代价函数的梯度正比于角度估计误差的特性，提出一种角度跟踪环路。角度跟踪环路进一步降低改进导向矢量匹配算法的运算代价。由于采用估计局部极值的策略代替原算法中全局最大值搜索策略，因而角度跟踪环路具有更优的相位噪声鲁棒性。

[1] Sundaram K R, Mallik R K, and Murthy U M S. Modulo conversion method for estimating the direction of arrival[J].2000, 36(4): 1391-1396.

[2] 袁孝康. 相位干涉仪测向定位研究[J]. 上海航天, 1999, 1(3): 1-6.

Yuan Xiao-kang. Study on direction-finding and position with phase interferometers[J]., 1999, 1(3): 1-6.

[3] 李东虎. 干涉仪测向系统中的基线配置技术[J]. 无线电工程, 2014, 44(4): 17-19.

Li Dong-hu. Baseline configuration technique in interferometer direction finding system[J]., 2014, 44(4): 17-19.

[4] 张亮, 徐振海, 熊子源, 等. 基于圆阵干涉仪的被动导引头宽带测向方法[J]. 系统工程与电子技术, 2012, 34(3): 462-466.

Zhang Liang, Xu Zhen-hai, Xiong Zi-yuan,. Wideband direction finding method of passive radar seeker based on circular array phase interferometer[J]., 2012, 34(3): 462-466.

[5] 周亚强, 陈翥, 皇甫堪, 等. 噪扰条件下多基线相位干涉仪解模糊算法[J]. 电子与信息学报, 2005, 27(2): 259-261.

Zhou Ya-qiang, Chen Zhu, Huangfu Kan,. Algorithm of solving multi-baseline interferometer phase difference ambiguity in noisy circumstance[J].&, 2005, 27(2): 259-261.

[6] 狄慧, 刘渝, 杨健, 等. 联合到达时间估计的长基线测向相位解模糊算法研究[J]. 电子学报, 2013, 41(3): 496-501.

Di Hui, Liu Yu, Yang Jian,. Long baseline direction finding unwrapping phase ambiguity algorithm with TOA estimation[J]., 2013, 41(3): 496-501.

[7] 朱旭东. 相关处理在干涉测向仪中的应用[J]. 现代雷达, 2003, 1(1): 22-25.

Zhu Xu-dong. Application of correlation method for interferometer direction finder[J]., 2003, 1(1): 22-25.

[8] 张敏, 郭福成, 周一宇, 等. 时变长基线2维干涉仪测向方法[J]. 电子与信息学报, 2013, 35(12): 2882-2888.

Zhang Min, Guo Fu-cheng, Zhou Yi-yu,. Direction finding method for two-dimension interferometer using the time varying long baseline[J].&, 2013, 35(12): 2882-2888.

[9] 刘建华, 彭应宁, 田立生. 基于方向向量空间距离的干涉仪测向处理方法[J]. 无线电工程, 1999, 29(1): 14-19.

Liu Jian-hua, Peng Ying-ning, and Tian Li-sheng. Space distance of steering vector based algorithm for DOA estimation with phase interferometer[J]., 1999, 29(1): 14-19.

[10] 李淳, 廖桂生, 李艳斌. 改进的相关干涉仪测向处理方法[J]. 西安电子科技大学学报, 2006, 33(3): 400-403.

Li Chun, Liao Gui-sheng, and Li Yan-bin. A DF method for the improved correlative interferometer[J]., 2006, 33(3): 400-403.

[11] 魏合文, 王军, 叶尚福. 一种基于余弦函数的相位干涉仪阵列DOA估计算法[J]. 电子与信息学报, 2007, 29(11): 2665-2668.

Wei He-wen, Wang Jun, and Ye Shang-fu. An algorithm of estimation direction of arrival for phase interferometer array using cosine function[J].&, 2007, 29(11): 2665-2668.

[12] Liu Guo-hong and Sun Xiao-ying. Efficient method of passive localization for mixed far-field and near-field sources[J]., 2013, 12: 902-905.

[13] Zhi Wan-jun and Chia Yan-wah. Near-field source localization via symmetric subarrays[J]., 2007, 14(6): 409-412.

[14] Liu Guo-hong and Sun Xiao-ying. Two-stage matrix differencing algorithm for mixed far-field and near-field sources classification and localization[J]., 2014, 14(6): 1957-1965.

[15] 虞飞, 陶建武, 李京书. 相干声波信号DOA单快拍矢量平滑估计与跟踪算法[J]. 电子学报, 2011, 39(12): 2733-2740.

Yu Fei, Tao Jian-wu, and Li Jing-shu. Direction finding and subspace tracking of coherent acoustic signals with single snapshot smoothing based on vector sensor array[J]., 2011, 39(12): 2733-2740.

[16] 刘亮, 陶建武, 黄家才. 基于稀疏对称阵列的近场源定位[J]. 电子学报, 2009, 37(6): 1307-1312.

Liu Liang, Tao Jian-wu, and Huang Jia-cai. Near-field source localization based on sparse symmetric array[J]., 2009, 37(6): 1307-1312.

[17] 韩月涛, 吴嗣亮, 王堃, 等. 一种基于有限记忆算法的干涉仪解模糊纠错方法[J]. 宇航学报, 2012, 33(1): 120-127.

Han Yue-tao, Wu Si-liang, Wang Kun,. An ambiguity- resolving error correction method of interferometer based on limited memory algorithm[J]., 2012, 33(1): 120-127.

Estimating and Tracking Angle of Arrival via Phase Interferometer with Symmetric Array

Wei Zi-xiang①Hu Yong-fang②Cui Wei①Wu Si-liang①

①(,,100081,)②(,201108,)

The exiting algorithms for Angle Of Arrival (AOA) estimation of incident signal via phase interferometer may degrade significantly for near-field target. To deal with this issue, a Modified Steering Vector Matching (MSVM) algorithm with the good performance in both far field and near field is proposed. Symmetric array is employed to receive signal. The phase difference of antennas in symmetric position is independent on range as the terms related to range in arriving phases are cancelled. Accordingly, a cost function, which is only related to the AOA in near field, is derived, and the AOA of incident signal can be estimated by finding the maximal value of the cost function. Based on MSVM algorithm, an angle tracking loop is proposed by employing the feature that the gradient of cost function is proportional to the angle error. As a fast algorithm for finding local extremum of cost function, angle tracking loop is obviously more robust than other algorithm searching global maximum in terms of phase noise. Simulations are implemented to verify the excellent performance of angle tracking loop under different phase noise and range scenarios.

Signal processing; Phase interferometer; Angle tracking loop; Symmetric array; Angle Of Arrival (AOA) estimate

TN971

1009-5896(2015)10-2369-08

10.11999/JEIT150013

2015-01-05；改回日期：2015-05-04；

2015-06-18

崔嵬 cuiwei@bit.edu.cn

上海航天科技基金(SAST201215)和新世纪优秀人才支持计划(NCET-13-0034)

The Foundation of Shanghai Aerospace Science and Technology (SAST201215); The Program for New Century Excellent Talents in University (NCET-13-0034)

魏子翔：男，1987年生，博士生，研究方向为扩频信号处理.

胡永芳：女，1970年生，高级工程师，研究方向为空间飞行器总体设计暨空间电源控制系统.

崔嵬：男，1976年生，教授，博士生导师，研究方向为空间合作/非合作目标无线电探测与定位、信号处理理论与应用.