一种快速DSmT-DS近似推理融合方法

郭 强 何 友 李新德



一种快速DSmT-DS近似推理融合方法

郭 强*①何 友①李新德②

①(海军航空工程学院信息融合技术研究所 烟台 264001)②(东南大学复杂工程测量与控制教育部重点实验室 南京 210096)

该文对Dempster-Shafer(DS)理论以及Dezert-Smarandache理论(DSmT)进行了深入研究，为了能够在仅需较低计算复杂度的前提下得到更加精确的融合结果，提出一种新的快速DSmT-DS近似推理融合方法。该方法针对超幂集空间仅单子焦元具有信度赋值的情况，将超幂集空间拆分映射成元素为各单子焦元和其补集的二元集合的新的超幂集空间，并求出每个补集的信度赋值；再运用Dezert-Smarandache框架中的第5条比例冲突分配规则(DSmT+PCR5)在新的超幂集空间的二元集合子空间下对多证据源进行融合，得到各单子焦元的融合结果；然后通过归一化处理求得各单子焦元的信度赋值。通过理论分析得出该文方法的融合结果是介于Dezert-Smarandache框架中的第5条比例冲突分配规则(DSmT+PCR5)及Dempster-Shafer(DS)框架下的 Dempster 组合规则之间。该文方法在需要较低计算复杂度的前提下，可以得到优于Dempster组合规则的近似融合结果。最后通过多个角度与已有方法进行对比，验证了该文方法的优越性。

信息融合；证据理论；Dezert-Smarandache理论；近似推理；拆分映射

1 引言

信息融合技术作为一门蓬勃发展的新兴关键技术，由于可以将多个信源采集的不完整信息加以综合，减少多源信息间可能存在的冗余和矛盾信息，降低其不确定性，提高智能系统决策、规划、反应的快速正确性，近年来得到国内外学者的广泛重视，并在军事和国民经济等多个领域得到了广泛的应用。随着信息环境的日益复杂，越来越多的信息获取、融合和智能决策系统对于如何高效地融合高冲突、不完善、不精确的不确定证据信息提出了更高的要求。DSmT理论(Dezert-Smarandache Theory)是由文献[5]提出的一种新的处理不确定、高度冲突和不精确的证据源的融合问题的有效方法。它可以看作是DST理论(Dempster-Shafer Theory)的扩展，却不受DS (Dempster-Shafer)框架的限制，可以有效处理复杂的静态或动态融合问题，特别是当信息源间的冲突非常大时，或者是所考虑问题的框架中命题之间的界限模糊、不确定、不精确而很难细分时，DSmT都发挥了它的优势[6,7]。目前该理论方法已在图像处理、机器人环境感知、军事上的多目标跟踪与识别、故障诊断、雷达目标分类等领域都得到了广泛的应用。而现阶段推广和应用DSmT最突出的瓶颈问题是，随着鉴别框架中焦元数目的增多，其组合推理运算成指数级增长。

为了解决这一问题，文献[13,14]提出一种快速分层递阶的DSmT近似推理融合方法。该方法的融合结果在保持与DSmT经典方法融合结果较高信息相似度的前提下，计算量显著减少，较好地解决了DSmT的计算瓶颈问题。但该方法在信息源存在较高的冲突时，正确结果焦元的信度赋值会向其它焦元转移，导致各焦元的信度赋值融合结果较平均，对冲突证据源敏感性弱，而且该方法需要对每一个二叉树分组的焦元进行Dezert-Smarandache框架中的第5条比例冲突分配规则(Proportional Conflict Redistribution No.5 within Dezert- Smarandache framework, DSmT+PCR5)融合计算，分组的粒度随着焦元数目的增多而增多，导致计算量仍然较大。

因此，本文提出一种新的快速DSmT-DS近似推理融合方法。该方法针对仅单子焦元具有信度赋值情况，将超幂集空间拆分映射成元素为各单子焦元和其补集的二元集合的新的超幂集空间，并求出新超幂集空间中每个子空间中单焦元的补集的信度赋值。然后运用DSmT+PCR5规则分别在映射形成的新的超幂集空间的二元集合子空间下对证据源进行融合，得到各单子焦元的融合结果，最后通过归一化求得每一个单子焦元的信度赋值。通过理论分析得出本文方法求得的融合结果是介于DSmT+ PCR5及Dempster规则之间且优于Dempster规则的近似融合结果。通过计算复杂度分析得出，本文方法计算复杂度极小。仿真实验结果表明，该方法不仅计算复杂度极小，融合结果相似度更高，而且对于高冲突信息的融合问题，相比已有的近似融合方法，可以得到一个更精确的近似融合结果。

2 基本理论

2.1 DS框架下的Dempster组合规则

2.2 DSm框架下的PCR5融合规则

其中，卷入式(3)中所有的元素都是规范形式，当证据信息模型为DS模型时，等价于幂集空间，当证据信息模型为存在约束的混合DSm模型时，等价于超幂集空间,代表为中的任意非空焦元，代表中与没有交集的非空焦元，

3 一种快速DSmT-DS近似推理融合方法

本文提出一种快速DSmT-DS近似推理融合方法，该方法程序流程如图1所示。其主要步骤为：

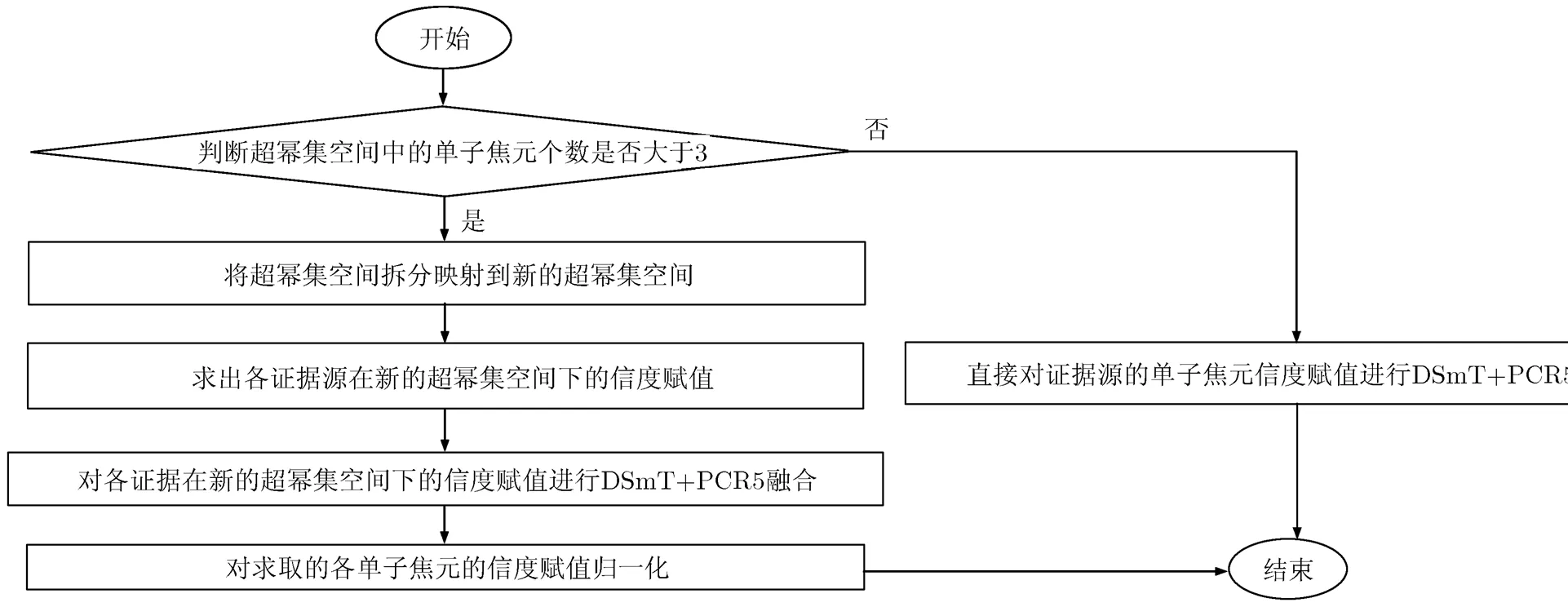
图1 快速DSmT-DS近似推理融合方法程序流程图

步骤5 对步骤4求得的各单子焦元的信度赋值进行归一化处理。

3.1超幂集空间拆分映射

3.2求新超幂集空间的各单子焦元信度赋值

由3.1节可知，映射生成的新超幂集空间的元素不是传统意义上的单焦元或多焦元，而是由单焦元和它的补集构成的二元集合子空间，如其中的第个元素，也称子空间，由单子焦元和其补集=构成，其补集的信度赋值为

3.3对新的超幂集空间的子空间进行DSmT+PCR5融合

对两证据源在新的超幂集空间中对应的相同单子焦元和其补集的子空间进行DSmT+PCR5融合推理得到各单子焦元的信度赋值为

3.4 归一化处理

从DSmT+PCR5规则式(3)分析可知，当使用单子焦元的补集的信度赋值取代补集中各焦元的信度赋值求得，由于补集为一个焦元相比各单子焦元对于的信度赋值强度更强，融合过程中冲突焦元的信度赋值会有一部分按照比例转移给了，而使减少，，本文通过将3.3节得到的初步融合结果归一化，平均了各焦元损失的信度赋值，得到单焦元的最终的信度赋值，即

4 分析快速DSmT-DS融合结果与DSmT+ PCR5及Dempster规则融合结果的关系

对式(7)和式(8)进行分析，得出本文方法融合结果与DSmT+PCR5及 Dempster组合规则融合结果的关系。令,,DSmT+PCR5规则中对的每一项的冲突分配表示为和,，即如果使用DSmT+PCR5规则，得出的焦元的基本信度赋值为

5 计算复杂度对比分析

针对仅有两个证据源，且超幂集空间中仅单子焦元有信度赋值(,代表焦元个数)的情况，首先直接采用DSmT+PCR5方法(以下简称经典方法)对两证据源融合过程进行计算复杂度分析，然后对文献[13]方法进行计算复杂度分析，最后对本文提出的快速DSmT-DS近似推理融合方法(以下简称本文方法)进行分析，通过计算复杂度的理论分析对比3种方法的计算效率。

6 仿真实验结果对比分析

为了验证本文方法的优越性，本文从融合结果的相似性、方法的高效性、冲突敏感性及鲁棒性4个指标在相同的实验条件下对多种方法进行对比分析。

6.1融合结果的相似性

采用Euclid相似度函数[17]对融合结果进行相似度分析

本文采取蒙特卡洛仿真试验对比3种方法的融合结果。假设给定两证据源，，对每个证据源的超幂集空间中的焦元进行随机的非零信度赋值。分别进行1000次蒙特卡洛仿真实验，将每次实验随机产生的一对证据，分别利用经典方法、文献[13]方法和本文方法得到融合结果，并计算与经典方法融合结果的相似度，每次的实验结果如图2及表1所示。(本文所有仿真实验是通过Pentimu(R) Dual-Core CPU E5300 2.6 GHz 2.59 GHz, 1.99 GB内存的计算机进行Matlab仿真实现的。)

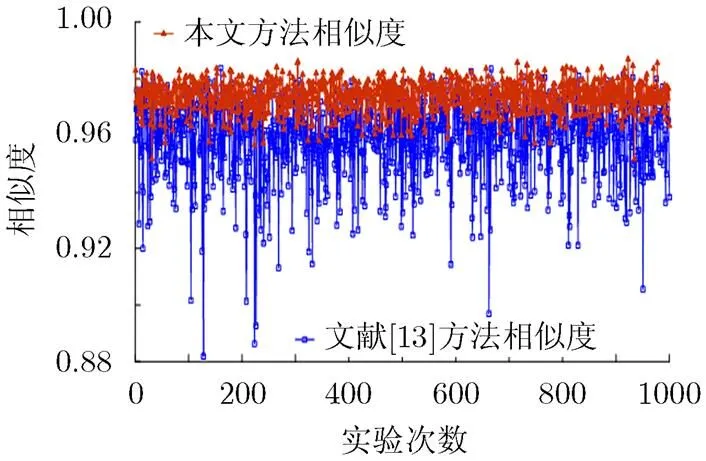
图2 超幂集空间焦元数目为20情况下的蒙特卡洛仿真实验相似度对比

表1融合结果对比分析表

经过1000次蒙特卡罗仿真实验，本文方法与经典方法融合结果的平均相似度略高于文献[13]方法与经典方法融合结果的平均相似度，且最低相似度在95%以上，说明了本文方法融合结果的高相似性。

6.2 融合方法的高效性

第5节已经做过了计算复杂度的理论分析，但为了更直观体现本文方法的高效性，通过表2中含有不同焦元数量的超幂集空间的两个证据源融合算例，比较3种方法的运算性能。

表2 3种方法在不同焦元数量的超幂集空间中运算性能比较

从表2可知，本文方法加法运算次数小于文献[13]方法的1/3，乘法运算次数小于文献[13]方法的1/2，除运算次数小于文献[13]方法的1/4，其增加的焦元个数的减法运算，由于减法运算量极小，对运算复杂度影响很小，本文算法计算复杂度相比于其他方法极小。

6.3冲突敏感性

为了验证本文方法可以有效融合冲突证据源信息，这里假设两个冲突证据源的超幂集空间为，其上的信度赋值如表3所示。

表3两冲突证据源信度赋值算例

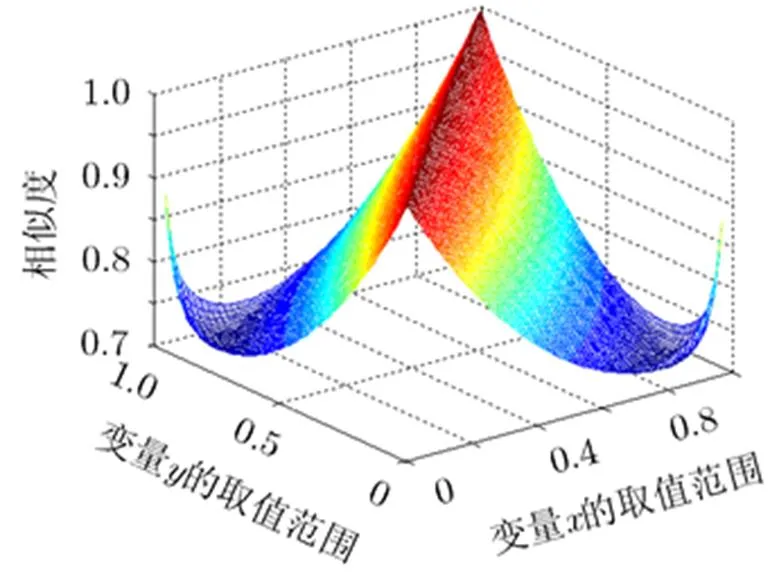
图3 文献[13]方法与经典方法对冲突证据信息融合结果的相似度

图4 本文方法与经典方法对冲突证据信息融合结果的相似度

6.4 鲁棒性

分析可知，同时改变焦元的赋值顺序不会影响经典方法的融合结果，因为经典方法是通过各单子焦元与其余各焦元的信度运算求得融合结果的，而本文方法是通过各单子焦元与其补集焦元的信度运算求得融合结果的，其融合结果也不随着焦元赋值顺序的改变而改变，随机给出如表4所示的3个证据源情况的各单子焦元的信度赋值，其焦元次序和信度赋值次序同时变化时，本文仿真的融合结果不发生变化，且其与经典方法的相似度为0.9610，证明了本文方法具有很强的鲁棒性。

表4多证据源情况的融合结果比较

7 结束语

DSmT作为一种新的解决高冲突信息融合处理问题的有效方法，已经在多个领域得到了广泛的应用，但是随着其鉴别框架焦元数目的增多导致其融合结果的计算呈组合爆炸的固有瓶颈一直无法突破，对该问题的解决不仅有着重要的理论价值，更有着巨大的应用价值。基于此，本文研究并提出了一种快速DSmT-DS近似推理融合方法，相比已有的近似推理方法，本文方法在保证了融合结果准确率的前提下，计算复杂度极小，计算效率显著提高，有效地解决了DSmT的计算瓶颈问题。

本文进行的DSmT近似算法的研究是建立在超幂集空间中交多子焦元为0的情况下，对超幂集空间存在交多子焦元信度赋值的复杂情况尚未进行深入研究。在实际应用中的融合信息高冲突背景下，即使在DS模型下，Dempster组合规则容易产生悖论无法得到较好的结果而使用DSmT+PCR5进行融合可以得到更符合实际的结果[5]，在这种情况下，本文方法可以有效取代DSmT+PCR5。接下来，还要做两方面的研究，一是如何在尽量不提高方法计算复杂度的前提下，进一步提高近似算法的精度；二是研究在超幂集空间中存在多子焦元的情况下，如何有效进行DSmT融合推理计算。

参考文献

[1] 史亚, 姬红兵, 朱明哲, 等. 多核融合框架下的雷达辐射源个体识别[J]. 电子与信息学报, 2014, 36(10): 2484-2490.

Shi Ya, Ji Hong-bing, Zhu Ming-zhe,.. Specific radar emitter identification in multiple kernel fusion framework [J].&, 2014, 36(10): 2484-2490.

[2] 李程, 王伟, 施龙飞, 等. 基于多源信息融合的有源雷达组网方式序贯识别方法[J]. 电子与信息学报, 2014, 36(10): 2456-2463.

Li Cheng, Wang Wei, Shi Long-fei,.. Sequential method for netting type recognition of active radars based on multi-source information fusion [J].&, 2014, 36(10): 2456-2463.

[3] 杨露, 沈怀荣, 周伟静, 等. 基于信息融合的故障诊断集成平台设计与实现[J]. 系统仿真学报, 2014, 26(1): 132-136.

Yang Lu, Shen Huai-rong, Zhou Wei-jing,.. Design and realization of fault diagnosis platform based on information fusion[J]., 2014, 26(1): 132-136.

[4] 李嘉菲, 周斌, 刘大有, 等. 海量信息融合方法及其在状态评价中的应用[J]. 软件学报, 2014, 25(9): 2026-2036.

Li Jia-fei, Zhou Bin, Liu Da-you,.. Massive information fusion algorithm and its application in status evaluation[J]., 2014, 25(9): 2026-2036.

[5] Smarandache F and Dezert J. Advances and Applications of DSmT for Information Fusion: Vol 3[M]. USA: American Research Press, 2009: 54-58.

[6] Li X, Dezert J, Smarandache F,.. Combination of qualitative information with 2-Tuple Linguistic Representation in DSmT[J]., 2009, 24(4): 786-798.

[7] Li X, Dai X, Dezert J,.. Fusion of imprecise qualitative information[J]., 2010, 33(3): 340-351.

[8] Li X, Huang X, Dezert J,.. A successful application of DSmT in sonar grid map building and comparison with DST-based approach[J]., 2007, 3(3): 539-551.

[9] 李新德, 黄心汉, 戴先中, 等. 基于DSmT融合机的移动机器人环境感知研究[J]. 华中科技大学学报, 2009, 37(12): 64-67.

Li Xin-de, Huang Xin-han, Dai Xian-zhong,.. Study on environment perception of mobile robots using DSmT-based fusion machine[J]., 2009, 37(12): 64-67.

[10] 辛玉林, 邹江威, 徐世友, 等. DSmT理论在综合敌我识别中的应用[J]. 系统工程与电子技术, 2010, 32(11): 2385-2388.

Xin Yu-lin, Zou Jiang-wei, Xu Shi-you,.. Application of DSmT in integrated identification of friend-or-foe[J]., 2010, 32(11): 2385-2388.

[11] 覃东升, 苗壮, 王勇. 改进的DSmT算法及其在C4ISR系统中的应用[J]. 电子科技大学学报, 2014, 43(4): 592-595.

Qin Dong-sheng, Miao Zhuang, and Wang Yong. Improved method based on DSmT and its application in C4ISR system[J]., 2014, 43(4): 592-595.

[12] 李新德, 潘锦东, Jean D. 一种基于DSmT和HMM的序列飞机目标识别算法[J]. 自动化学报, 2014, 40(12): 2862-2876.

Li Xin-de, Pan Jin-dong, and Jean D. A target recognition algorithm for sequential aircraft based on DSmT and HMM[J]., 2014, 40(12): 2862-2876.

[13] 李新德, Jean D, 黄心汉, 等. 一种快速分层递阶DSmT 近似推理融合方法(A)[J]. 电子学报, 2010, 38(11): 2566-2572.

Li Xin-de, Jean D, Huang Xin-han,.. A fast approximate reasoning method in hierarchical DSmT(A)[J]., 2010, 38(11): 2566-2572.

[14] 李新德, 杨伟东, 吴雪建, 等. 一种快速分层递阶DSmT 近似推理融合方法(B)[J]. 电子学报, 2011, 39(3A): 31-36.

Li Xin-de, Yang Wei-dong, Wu Xue-jian,.. A fast approximate reasoning method in hierarchical DSmT(B)[J]., 2011, 39(3A): 31-36.

[15] 邓勇, 王栋, 李齐, 等. 一种新的证据冲突分析方法[J]. 控制理论与应用, 2011, 28(6): 839-844.

Deng Yong, Wang Dong, Li Qi,.. A new method to analyze evidence conflict[J].&2011, 28(6): 839-844.

[16] 蒋雯, 彭进业, 邓勇. 一种新的证据冲突表示方法[J]. 系统工程与电子技术, 2010, 32(3): 562-565.

Jiang Wen, Peng Jin-ye, and Deng Yong. New representation method of evidential conflict[J]., 2010, 32(3): 562-565.

[17] Li X, Jean D, Smarandache F,.. Evidence supporting measure of similarity for reducing the complexity in information fusion[J]., 2011, 181(10): 1818-1835.

Fast DSmT-DS Approximate Reasoning Method

Guo Qiang①He You①Li Xin-de②

①(,,264001,)②(,,210096,)

In this paper, Dempster-Shafer (DS) theory and Dezert-Smarandache Theory (DSmT) are conducted thorough reasearch, and in order to obtain more accurate fusion results in the premise of needing less computation complexity, a fast DSmT-DS approximate reasoning method is proposed. This method is only fit for the case that there are only singleton focal elements with assignments in hyper-power set. The hyper-power set is splitted and mapped to a new hyper-power set which consists of the binary sets of the focal element and its complementary set to the assignments of the complementary sets are computed. Proportional Conflict Redistribution No.5 within Dezert-Smarandache framework (DSmT+PCR5) is applied to fuse the multi-source evidence in the binary sets of the new hyper-power set to get the fusion results of singleton focal elements. Then the assignments of singleton focal elements are obtained by normalization. Through the theoretical analysis, the conclusion is drawn that the fusion results of the mothod in this paper is between the results of DSmT+PCR5 and Dempster’s combination rule based on DS model, and the fusion results of the method in this paper which is better than the rusults of Dempster’s combination rule can be obtained in the premise of minimal computation complexity. Finally, by comparing the method in this paper with the existing methods from different views, the superiority of new one is testified well.

Information fusion; Evidence theory; Dezert-Smarandache Theory (DSmT); Approximate reasoning; Splitting mapping

TP391

A

1009-5896(2015)09-2040-07

10.11999/JEIT150086

郭强 gq19860209@163.com

2015-01-15收到，2015-03-27改回，2015-06-29网络优先出版

国家自然科学基金(61102166, 61471379)和山东省优秀中青年科学家科研奖励基金(BS2013DX003)资助课题

郭 强： 男，1986年生，讲师，研究方向为信息融合、辐射源识别、态势评估、DSmT、证据网络等.

何 友： 男，1956年生，教授，中国工程院院士，研究方向为信息融合等.

李新德： 男，1975年生，副教授，研究方向为DSmT、信息融合、自动导航、多传感器多目标跟踪、目标自动识别等.