基于模糊子空间聚类的〇阶L2型TSK模糊系统

2015-10-14邓赵红张江滨蒋亦樟史荧中王士同

电子与信息学报 2015年9期

邓赵红张江滨蒋亦樟史荧中王士同

邓赵红*张江滨蒋亦樟史荧中王士同

(江南大学数字媒体学院无锡 214122)

经典数据驱动型TSK(Takagi-Sugeno-Kang)模糊系统在获取模糊规则时，会考虑数据的所有特征空间，其带来一个重要缺陷：如果数据的特征空间维数过高，则系统获取的模糊规则繁杂，使系统复杂度增加而导致解释性下降。该文针对此缺陷，探讨了一种基于模糊子空间聚类的〇阶L2型TSK模糊系统(Fuzzy Subspace Clustering based zero-order L2- norm TSK Fuzzy System, FSC-0-L2-TSK-FS)构建新方法。新方法构建的模糊系统不仅能缩减模糊规则前件的特征空间，而且获取的模糊规则可对应于不同的特征子空间，从而具有更接近人类思维的推理机制。模拟和真实数据集上的建模结果表明，新方法增强了面对高维数据所建模型的解释性，同时所建模型得到了较之于一些经典方法更好或可比较的泛化性能。

Takagi-Sugeno-Kang(TSK)模糊系统；医疗诊断；解释性；高维数据

1 引言

模糊系统是以模糊集合[1]和模糊推理理论为基础演变而来的一种人工智能系统，其主要特点是能够将自然界的模糊语言转化成与人类推理机制相似的模糊规则。目前，模糊系统已被广泛应用于各个领域，如图像处理、智能决策等[2,3]。与其他的人工智能技术相比，模糊系统不仅具有强大的学习能力，而且具有高度解释性[4,5]。模糊系统凭借这一独特优势，在医疗诊断中被广泛应用[6,7]。当一种智能模型在医疗诊断中被应用时，人们希望它具有强的解释能力和良好的可靠性。模糊系统通过模糊推理机制，对某种医学疾病建立相应的模糊规则，模拟专家诊断疾病的过程，帮助医生解决复杂的医学诊断问题。

在已有的几种经典模糊系统中，Takagi-Sugeno- Kang(TSK)[8,9]模糊系统由于其输出的简洁性和良好的逼近性能被广泛探讨和运用[10,11]。不同于早期基于专家经验的模糊系统构建方法，数据驱动型模糊系统正日益成为最主要的模糊系统构建方法。经典数据驱动型TSK模糊系统在模型训练过程中，采用训练样本的全部特征来构建模糊规则。而对于模糊逻辑系统来说，其解释性主要来自于模糊规则中的模糊集可对应于人类的语言描述，故经典TSK模糊系统在对高维数据进行训练时，会因采用大量的特征而使其规则太复杂，使得清晰度和解释性下降。在医疗诊断中，要求系统具有很强的解释性，而大量医学数据都具有较高的特征空间。若将经典TSK模糊系统用于医疗检测，势必导致系统的解释性骤降。本文所提出的FSC-0-L2-TSK-FS模型能够利用FSC聚类，将模糊规则映射到不同子空间。当从高维数据中获取模糊规则时，规则前件并不需要数据的全部特征，而是采用FSC聚类所抽取的子空间特征，从而有效地降低了所建模型的复杂性，增强了规则的清晰度和解释性。将FSC-0-L2-TSK-FS模型与医疗诊断相结合，每条模糊规则可从不同的视角(特征空间)对疾病进行医疗诊断，更符合专家诊断的推断过程。

2 高维数据驱动的模糊系统建模

2.1 经典TSK模糊系统简介

根据文献[12]，经典模糊系统包括Takagi- Sugeno-Kang模糊系统模型(TSK-FS), Mamdani- Larsen模糊系统模型(ML-FS)[13]和广义模糊系统模型(GFM)[14]。由于TSK模型的广泛应用，本文以该模型为例探讨高维数据驱动的模糊系统建模以及面临的挑战。对于经典TSK模糊模型，其模糊规则定义如下。

若将乘算子、加算子分别作为合取和析取操作算子，加法算子作为组合算子，同时采用重心反模糊操作，经过去模糊化之后，最终的输出可表示为

2.2 经典TSK模糊系统高维数据之挑战

实践表明，经典TSK模糊系统在处理高维数据时，其解释性和简洁性下降严重，具体表现在以下两方面。

3 基于模糊子空间聚类的〇阶L2型TSK模糊系统建模

3.1模糊规则构建

根据2.2节所提出的经典TSK模糊系统之不足，本文探讨了一种基于模糊子空间聚类的〇阶L2型TSK模糊系统(Fuzzy Subspace Clustering based zero-order L2-norm TSK Fuzzy System, FSC-0-L2- TSK-FS)构建方法，其所对应的模糊规则如下。

与经典TSK模糊系统规则相比，该规则具有如下特色。

3.2基于模糊子空间聚类的规则前件学习

模糊子空间聚类[15](FSC)能将高维数据空间转化到其相关的子空间中进行聚类。在模糊子空间聚类中，每一类给定权重向量，用于表示不同的特征(维度)对于该类的贡献程度。FSC-0-L2-TSK-FS可根据FSC中特征权重思想，为规则抽取重要特征。根据文献[16]，FSC的优化目标函数及其约束条件可写成

FSC-0-L2-TSK-FS模型的每条模糊规则对应输入向量的特征子空间，特征子空间又与模糊子集对应。若采用高斯隶属函数作为模糊子集的隶属度函数，第条规则的模糊子集的隶属函数可以表示为

根据3.2节规则前件的特征选取以及式(3)，FSC-0-L2-TSK-FS模型的输出可以表示成

其中

则式(10)可表示成

类似于L2-SVR[20]的学习原理，在引入结构风险项和正则化项之后，最终的优化目标函数可表示成

通过最优化理论，将式(18)转化为对偶问题：

最终，根据3.2节获取的FSC-0-L2-TSK-FS规则前件，以及本小节运用二次规划理论求解得到的模糊规则后件参数，整合得到FSC-0-L2-TSK-FS模型和模糊规则库。

4 实验研究

4.1 实验设置

实验部分分别采用模拟数据集和UCI中的Heart，Breast数据集进行实验评估和验证。本文选取3种经典TSK模糊系统模型作为对比算法，分别为基于-不敏感损失函数的L2型TSK模糊系统[18](L2-TSK-FS)，基于IQP优化算法的-不敏感损失函数的TSK模糊系统[17](-TSK-FS(IQP))、基于LSSLI优化算法的-不敏感损失函数的TSK模糊系统[17](-TSK-FS(LSSLI))。实验中，采用5倍交叉验证策略对参数进行寻优。其中，模糊规则数的寻优集合为{2,3,4,5,6,7,8,9,10,11,25,32}；高斯函数尺度参数的寻优集合为；规则化参数的寻优集合为；特征选取参数的寻优集合为{0.6,0.62, 0.64,,1.2}；FSC模糊指数参数的寻优集合为{1.05,1.5,5,10,50,100,1000}。

为对各算法所得模型的泛化性能进行对比，采用分类正确率作为实验评价指标。正确率越接近1，说明模型的性能越好。为对所构建的模糊系统的复杂度进行对比，采用指标来描述模型的复杂度。其中表示模糊规则数目，表示第条模糊规则前件所抽取的特征数目，表示第条模糊规则后件参数个数。值越小，说明模型的规则复杂度越低，清晰度越高，语言解释性越强。

4.2模拟数据集实验

为体现模型适宜于高维数据和解释性强的特色，构造的模拟数据需具有如下特征：(1)具有较高的维数；(2)具有若干重要特征，并适当添加一些非重要特征和干扰项；(3)添加的重要特征需对应于不同的特征子空间。根据设置，生成400组30维4类分类数据。100组数据为一类，每类所对应的重要特征分别为1{3,7,12,18,25},2{6,7,8,9,10,11,12},3{15,17,19,21,23,24},4{2,7,12,17,22}。

算法的性能对比如表1所示。从中可以得出结论如下：(1)由于受到非重要特征强烈的干扰作用，3种经典TSK模型的系统性能下降严重，而FSC-0- L2-TSK-FS模型仍能保持良好的系统性能。(2)3种经典TSK模型采用模拟数据的全部特征(30个特征)来构建模糊规则。规则复杂度非常大，说明模糊规则太复杂，导致模型解释性下降严重。FSC-0-L2-TSK-FS模型只为规则选取一些重要特征，规则复杂度降低至105，增强了模型的清晰度和解释性。

表1模拟数据实验算法性能对比

FSC-0-L2-TSK-FS模型达到最优时，为每条模糊规则抽取的子空间特征如表2所示。通过表2可以发现，规则所抽取的子空间特征与模拟数据的重要特征绝大部分是相吻合的。说明FSC-0-L2-TSK- FS模型具有准确抓取数据重要特征的能力。图1所示为FSC-0-L2-TSK-FS模型的每条模糊规则空间特征分布情况。由图1可以看出，FSC-0-L2- TSK-FS模型通过FSC算法得到的聚类有着明显的子空间特征，其权值最高的几个特征恰好与表2所对应。

表2模拟数据实验FSC-0-L2-TSK-FS模型为每条规则抽取的特征

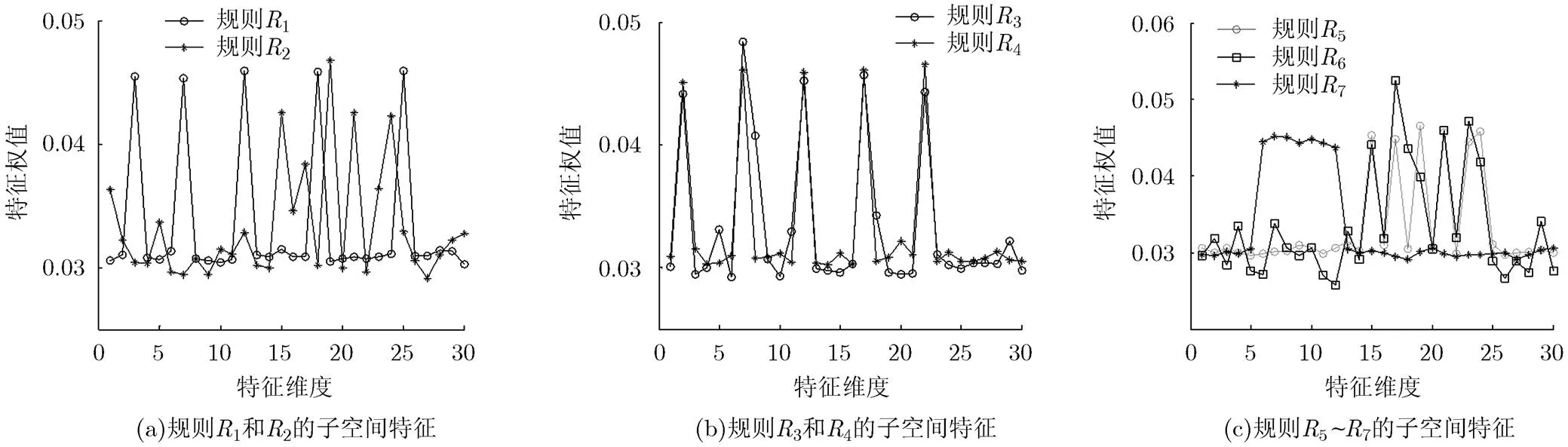
图1 模拟数据在FSC-0-L2-TSK-FS模型最优时每条规则的空间特征分布情况

4.3真实数据集仿真实验

本部分通过采用UCI机器学习库中的Heart, Breast数据集来进行实验。Heart数据集共有270组实验样本，每组样本有13个特征(维度)。270组实验样本被分成两类，分别为正常类和心脏病类。Breast数据集共有699组数据，每组数据包含10个特征(维度)。699组数据中，有458组良性乳腺瘤病例和241组乳腺癌病例。

各算法的实验结果和评价指标如表3所示。通过表3可得出结论有：(1)与3种经典TSK模型相比，FSC-0-L2-TSK-FS模型的性能与其相差无几，在误差允许范围内。(2)3种经典TSK模型无法为规则抽取重要的子空间特征，导致规则复杂度很高。FSC-0-L2-TSK-FS可为规则抽取重要子空间特征，规则复杂度分别降低至32和47，增强了规则的简洁性和解释性。

表3 UCI数据实验算法性能对比

为进一步验证FSC-0-L2-TSK-FS所构建的模型解释性增强之特性，选取L2-TSK-FS作为对比算法，选取Breast数据作为对比数据。表4为L2-TSK- FS达到最优时为每条规则抽取的特征及其高斯隶属函数表示和结论部分描述；表5为FSC-0-L2- TSK-FS达到最优时为每条规则抽取的特征及其高斯隶属函数表示和结论部分描述。通过对比可得出结论：(1)规则前件。L2-TSK-FS为每条规则选用全部的特征，每一特征对应于一个模糊子集。对于模糊逻辑系统来说，其解释性主要来自于模糊规则中的模糊集可对应于人类的语言描述。L2-TSK-FS模型因规则中含有的模糊子集太多，导致模型的解释性下降。FSC-0-L2-TSK-FS为每条规则抽取不同的特征，并且不同规则对应不同的特征子空间。这样可使获取的模糊规则更加易于语言描述，也使得模糊规则从不同的视角对问题进行推理，增强了模型的简洁性和解释性。(2)规则后件。L2-TSK-FS的后件为特征向量的线性组合形式，使得后件繁杂，简洁性下降；L2-TSK-FS的规则后件为常数，增强了规则后件的简洁性。

表4 L2-TSK-FS为每条规则抽取的特征及其高斯隶属函数表示(Breast)

表5 FSC-0-L2-TSK-FS为每条规则抽取的特征及其高斯隶属函数表示(Breast)

5 结束语

本文通过利用FSC聚类中的特征权值矩阵，构造出一种FSC-0-L2-TSK-FS模型。新方法能运用较少的重要特征来构建模糊规则，每条模糊规则对应于数据的特征子空间；具有较强的去噪能力，能够去除掉对系统稳定性干扰强的特征，保证了系统的鲁棒性；能准确把握住数据中的重要特征，所构建的模糊规则对应于不同的特征子空间，推理的侧重点不相同，更加符合人类的推理机制，增强了模型的解释性。

目前，FSC-0-L2-TSK-FS模型仍具有一定的缺陷。若给出的训练数据子空间特征不明显，会因丢失特征而导致系统泛化性能下降。如何从子空间特征不明显的高维数据中获取具有更强解释性的模糊系统是今后将进行的工作。

参考文献

[1] Zadeh L A. Fuzzy sets[J]., 1965, 8(3): 338-353.

[2] 李奕, 吴小俊. 基于监督学习的Takagi Sugeno Kang模糊系统图像融合方法研究[J]. 电子与信息学报, 2014, 36(5): 1126-1132.

Li Yi and Wu Xiao-jun. A novel image fusion method using the Takagi Sugeno Kang fuzzy system based on supervised learning[J].&, 2014, 36(5): 1126-1132.

[3] 宋恒, 王晨, 马时平, 等. 基于非单点模糊支持向量机的判决反馈均衡器[J]. 电子与信息学报, 2008, 30(1): 117-120.

Song Heng, Wang Chen, Ma Shi-ping,A decision feedback equalizer based on non-singleton fuzzy support vector machine[J].&, 2008, 30(1): 117-120.

[4] Lughofer E. On-line assurance of interpretability criteria in evolving fuzzy systems–achievements, new concepts and open issues[J]., 2013(251): 22-46.

[5] Riid A and Rüstern E. Adaptability, interpretability and rule weights in fuzzy rule-based systems[J]., 2014(257): 301-312.

[6] Thong N T and Son L H. HIFCF: an effective hybrid model between picture fuzzy clustering and intuitionistic fuzzy recommender systems for medical diagnosis[J]., 2015, 42(7): 3682-3701.

[7] Sanz J A, Galar M, Jurio A,Medical diagnosis of cardiovascular diseases using an interval-valued fuzzy rule-based classification system[J].ng, 2014(20): 103-111.

[8] Takagi T and Sugeno M. Fuzzy identification of systems and its applications to modeling and control[J].,,1985(1): 116-132.

[9] Sugeno M and Kang G T. Structure identification of fuzzy model[J]., 1988, 28(1): 15-33.

[10] Jiang Yi-zhang, Chung Fu-lai, Ishibuchi H,. Multitask TSK fuzzy system modeling by mining intertask common hidden structure[J]., 2015, 45(3): 548-561.

[11] Fadali S and Jafarzadeh S. TSK observers for discrete type-1 and type-2 fuzzy systems[J]., 2014, 22(2): 451-458.

[12] Chung Fu-lai, Deng Zhao-hong, and Wang Shi-tong. From minimum enclosing ball to fast fuzzy inference system training on large datasets[J]., 2009, 17(1): 173-184.

[13] Mamdani E H. Application of fuzzy logic to approximate reasoning using linguistic synthesis[J]., 1977, 100(12): 1182-1191.

[14] Azeem M F, Hanmandlu M, and Ahmad N. Generalization of adaptive neuro-fuzzy inference systems[J]., 2000, 11(6): 1332-1346.

[15] Gan Guo-jun and Wu Jian-hong. A convergence theorem for the fuzzy subspace clustering (FSC) algorithm[J]., 2008, 41(6): 1939-1947.

[16] Deng Zhao-hong, Choi Kup-sze, Chung Fu-lai,Enhanced soft subspace clustering integrating within-cluster and between-cluster information[J]., 2010, 43(3): 767-781.

[17] Leski J M. TSK-fuzzy modeling based on-insensitive learning[J].,2005, 13(2): 181-193.

[18] Deng Zhao-hong, Choi Kup-sze, Chung Fu-lai,Scalable TSK fuzzy modeling for very large datasets using minimal- enclosing-ball approximation[J].,2011, 19(2): 210-226.

[19] Juang Chia-feng and Chiang Loa. Zero-order TSK-type fuzzy system learning using a two-phase swarm intelligence algorithm[J]., 2008, 159(21): 2910-2926.

[20] Tsang I W, Kwok J T Y, and Zurada J M. Generalized core vector machines[J]., 2006, 17(5): 1126-1140.

Fuzzy Subspace Clustering Based Zero-order L2-norm TSK Fuzzy System

Deng Zhao-hong Zhang Jiang-bin Jiang Yi-zhang Shi Ying-zhong Wang Shi-tong

(,,214122,)

The classical data driven Takagi-Sugeno-Kang (TSK) fuzzy system considers all the features of trained data, and faces a challenge that the interpretation is degenerated and the obtained fuzzy rule is complex when trained by high dimensional data. In this paper, a new fuzzy model,.., Fuzzy Subspace Clustering based zero-order L2-norm TSK Fuzzy System (FSC-0-L2-TSK-FS) is proposed to overcome this difficulty. The proposed fuzzy system not only reduces the feature spaces of the rule of antecedent, but also makes different rules implement the inference indifferent subspaces. The inference mechanism of the proposed fuzzy model training algorithm is very similar to the inference procedure of human.The experimental studies on the synthetic and real datasets prove that the interpretation of model constructed by the proposed method is enhanced when trained by high dimensional data and the generalization performance is better or comparative to several classical TSK fuzzy systems training methods.

Takagi-Sugeno-Kang (TSK) fuzzy system; Medical diagnosis; Interpretability; High-dimensional data

TP391

1009-5896(2015)09-2082-07

10.11999/JEIT150074

邓赵红 dzh666828@aliyun.com

2015-01-13收到，2015-05-11改回，2015-06-29网络优先出版

国家自然科学基金(61170122)，江苏省杰出青年基金(BK20140001)和新世纪优秀人才支持计划(NCET120882)资助课题

邓赵红：男，1981年生，副教授，硕士生导师，研究方向为计算智能和模糊计算.

张江滨：男，1990年生，硕士生，研究方向为计算智能和模糊计算.

蒋亦樟：男，1988年生，博士生，研究方向为人工智能和模式识别.

史荧中：男，1970年生，博士生，研究方向为人工智能和模式识别.

王士同：男，1964年生，教授，博士生导师，研究方向为人工智能和模式识别.