采用路径分析方法定量分析影响棉纱强度的指标
2015-10-14李晓峰郁崇文
李晓峰,郁崇文
(东华大学 纺织学院,上海 201620)
采用路径分析方法定量分析影响棉纱强度的指标
李晓峰,郁崇文
(东华大学 纺织学院,上海 201620)
采用基于结构方程模型的路径分析方法,对棉纱强度的影响因素进行定量分析.研究了一定取值范围内棉纤维主体长度、断裂强度、线密度、马克隆值、短绒率、基数这6项纤维性能指标以及纱线线密度、捻度2项工艺指标对纱线强度的综合影响、直接影响及间接影响.通过分析发现,8个因素对棉纱强度影响的相关性都与定性分析所得结论一致.与定性分析相比,路径分析对各项指标对棉纱强度的直接与间接影响都给予了综合的定量表达,可以从中发现各项指标对成纱强度直接与间接影响程度的高低,对成纱前配棉纤维性能以及相关工艺指标的选取具有参考作用.
棉纱强度;结构方程模型;路径分析;路径系数;相关性分析
纱线强度是成纱质量的重要指标之一,直接决定了纺纱效率、纱线和织物的后整理工序以及织物的耐用性能,以及织造工序的顺利进行.纱线强度涉及的因素众多,受到包含纤维性能、纺纱工艺和纺纱方法等多方面的制约[1].到目前为止,研究棉纤维各项性能与环锭纱强度之间关系的报导很多,其大多采用单唛试纺方法,选择各项性能基本接近、只有一项性能有明显差异的几种棉纤维,然后进行相同工艺条件下单唛试纺,研究具有差异的这项性能指标对成纱强度的影响[1-2].部分文献选取少数几种不同取值范围的棉纤维性能指标,通过正交试验定性分析其对纱线强度的影响[2-5].利用多元统计分析方法研究多元变量之间的关系非常有效,然而在实际应用中由于涉及的影响因素众多,变量间又常常受到彼此的制约及共线性的影响,导致所建回归模型的准确度降低.在多元回归分析方法中,只有在自变量彼此之间完全独立的情况下,多元方程才能根据自变量的每单位变动对因变量的净影响作出可靠的估计.为了减少自变量间高度相关性带来的影响,本文利用结构方程模型建立路径分析,将各因素对纱线强度的影响分解为总影响、直接影响和间接影响,从而更清晰准确地对各因素与纱线强度之间的关系进行定量分析.
1 影响纱线强度的因素
1.1 纱线强度的构成
根据现有理论可知,纱线强度由两部分构成,一部分是断裂纤维的强力之和,另一部分是滑脱纤维的滑动摩擦力之和[1-3],即
P=Q+F
(1)
其中:P为纱线强度;Q为全部断裂纤维所构成可利用部分的强力;F为全部滑脱纤维所构成的滑动摩擦力.
1.2 成纱强度的影响因素
由式(1)可知,要提高纱线强度,需要同时考虑增加Q和F两个不同性质的受力,其中以增加Q为主.可以通过选取纤维的几个相关指标实现对Q的控制,主要包含以下几点[1-3]:(1)棉纤维断裂强度越高,成纱强度越高;(2)原棉短绒率越低、主体长度越长、基数(长度整齐度)越大,成纱强度越高;(3)纤维越细,纱线截面纤维根数越多,纤维断裂总根数增加,同时纤维间摩擦力也随之变大,纱线强度越高;(4)马克隆值过小、过大会通过影响纤维强力及纺纱性能,进而影响到纱线的强度;(5)加捻捻度控制纱线同时断裂纤维的根数以及纤维强力利用率高低.
2 基于结构方程模型的路径分析
2.1 结构方程模型中的路径分析与传统复回归分析
结构方程模型中的路径分析可以直接观察分析变量间的因果关系以及变量间的相关关系.传统的复回归分析是单相关分析,只描述变量间的相关程度,不考虑变量间的因果关系.与复回归分析相比,路径分析除了可以同时处理多组回归方程式的估计外,更重要的是对变量间的处理更加弹性.传统的复回归只探究路径系数的影响是否达到显著,无法就路径分析的假设模型做整体契合度的检验,也无法给出单个因子在多个影响因素共同作用下影响因变量程度的大小,并且无法确定这种判断的合理性.基于结构方程模型的路径分析在一定程度上解决了这个问题[6].
2.2 路径分析模型
路径分析中,自变量对因变量的作用包含直接效果与间接效果,两者之和称为自变量对因变量影响的总效果.
标准化回归分析模型如式(2)所示.
(2)
(i=1,2,…,p)

(3)
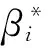
(4)
3 路径分析在棉纱强度分析中的应用
3.1 试验数据与分析工具
本文的试验数据样本来自邯郸某厂,包括9.7,14.6,18.2,29.2和36.4tex这5种不同线密度的普梳纱线共100组数据.每种试样分别由多批纤维单项性能指标在一定范围内变化的原棉纺成,并在一定范围内变动捻度大小,各指标取值范围如表1所示.根据前文分析,选择纤维的断裂强度(A)、线密度(B)、主体长度(C)、短绒率(D)、马克隆值(E)、基数(F)6个原棉指标以及纱线线密度(G)和捻度(H)2个工艺指标共8个参数作为模型的自变量,纱线强度作为因变量.同时,根据路径分析模型中的因果分析,将纱线线密度和捻度同时作为因变量与自变量存入路径分析模型中.这是由于一方面纱线线密度以及捻度受到纤维性能的影响,另一方面又直接影响了纱线的断裂强度.

表1 8种参数的取值范围Table 1 Value range of 8parameters
本文使用统计软件AMOS 17.0,在CPU为 2.3 GHz、内存为2 GB、硬盘为32 GB、Windows XP操作系统的计算机上进行路径图的建立、分析与验证.
3.2 各影响因子对纱线强度影响的路径分析
路径分析的实现工具是路径图,路径图中采用一条带箭头的连线连接两个变量,确定两个变量间预先设定的关系,单箭头连线表示两个变量间存在因果关系,双箭头连线表示两个变量间存在相关关系,双箭头表明变量间具有相关性,单箭头代表变量间因果关系发生的方向,箭头为果、箭尾为因.
AMOS操作系统可直接作出变量间的路径图,通过增列描绘或删除箭头符号可对路径图进行修正.全部以图标来描绘路径图的假设模型并进行参数估计是AMOS的一大特点.在分析过程中,主要根据模型拟合程度的验证性指标χ2值和显著性水平P值对路径分析模型进行反复调试和检验,只有当χ2值尽量小,并且P>0.05时,模型的拟合效果才能达到一定的可信程度.
根据实践经验,并经过不断验证和重复试验,得到与实际情况相符合并且通过拟合度检验的路径图如图1所示.模型得出的χ2=13.228,P=0.153>0.05,说明该模型可信.在结构方程模型检验中,研究者所期望获得的结果是“接受虚无假设”(不要拒绝虚无假设),因为一个不显著的检验结果,表示虚无假设不应被拒绝,则理论模型愈能契合实际数据的结构,模型的适配度愈佳[6].

图1 棉纱强度路径分析图Fig.1 Diagram of path analysis for cotton yarn intensity
由图1可以发现,棉纤维6个性能指标之间用双箭头连接,表明其两两相关,但影响有强有弱,可以通过路径图直接观察连线旁的相关系数大小得知.这同时也表明,棉纤维性能指标之间只存在相关或互为因果关系,不具有单向因果关系.
作为自变量的短绒率(D)、马克隆值(E),同时作为自变量和因变量的纱线线密度(G)与捻度(H)以及因变量棉纱断裂强度(I)都含有单箭头的连接线,线上的数据是自变量与因变量之间的标准化回归系数,即路径系数,定量表示了自变量排除其他因素干扰后对因变量的直接影响程度.中间变量及因变量右上方的数据表明该变量被其他有关变量所能解释的方差,即决定系数R2.纱线线密度、捻度以及纱线强度的决定系数都接近1,说明路径图所提供的指标变量及其关系足够决定纱线强度的大小,模型较合理.
路径图的结构方程组如下所示:
G=pDGD+pEGE+pe2Ge2
(5)
H=pFHF+pGHG+pe3He3=
pFHF+pGHpDGD+pGHpEGE+
pGHpe2Ge2+pe3He3
(6)

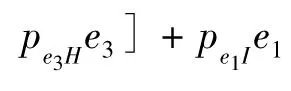
(7)
其中:pi j(i=A,B,…,I;j=A,B,…,I;i≠j)为变量i与j之间的路径系数.D、E和残差项e2共同决定G;F、G和残差项e3决定H;A~H和残差项e1共同影响I;残差项之间独立.
通过对原因变量和结果变量相关系数的分解,可以清楚地看出造成相关关系的各种原因.相关系数可由AMOS软件直接计算得出,本文样本变量间相关系数如表2所示.以纤维短绒率(D)与纱线线密度(G)之间的相关系数rDG及短绒率(D)与捻度(H)之间的相关系数rDH为例,对原因变量和结果变量的相关系数进行分解,如式(8)和(9)所示.由于各变量均经过标准化处理,所以D和G的相关系数rDG等于D和G乘积的期望值.另外,由于AMOS软件设置,路径图上所显示数据仅保留小数点后两位,为了减小误差,相关系数的分解计算采用更加精确的数值.

表2 样本变量间的相关系数Table 2 Correlation coefficients of the samples

(8)

(9)
由式(8)和(9)可以看出,D与G的相关系数可以分解为两部分:短绒率对纱线线密度的直接影响pDG,以及由于D和E具有相关性rDE,从而D间接引入了E对纱线线密度G的直接作用pEG,rDEpEG由此产生.从因果分析的角度,rDEpEG并未得到分解,既不是直接作用,也不是间接作用,而是由于原因变量之间的相关而引入的一项,一般称该项为未析部分,不出现在因变量对自变量的间接影响表格中.rDH中pGHpDG是短绒率(D)通过中间变量纱线线密度(G)对捻度(H)的间接影响.由表2可知,样本相关系数rDG和rDH分别为0.353和-0.305,与相关系数的分解计算出来的数值略有差异,主要是因为观察数据与假设模型很少存在完美适配的状况,二者之间总是存在某种程度的差异,假设模型与原数据拟合得越好,数值间的差异就越小.
自变量A,F,E,B,C,D对中间因变量G和H以及目标因变量I的总影响效果、直接影响效果以及间接影响效果分别如表3~5所示.从表3可以看出,纤维线密度(B)、马克隆值(E)、纤维主体长度(C)、纤维强度(A)、纱线线密度(G)、短绒率(D)、纱线捻度(H)、纤维基数(F)对纱线强度的影响依次减小,其中A,F,B,C,G和H的影响呈正相关,E和D的影响呈负相关,与实际生产中的情况一致.即短绒率越高,纱线强度越低;马克隆值过大,纤维过于成熟,纺纱性能差,纱线强度越低.综合各定量指标,可以为生产实践提供参考.如当限定原料性能指标在一定取值范围内,生产某线密度的普梳纱线时,选取较大的纤维强度(A)、基数(F)、线密度(B)、主体长度(C)和纱线捻度(H),以及较小的马克隆值(E)和短绒率(D),可得到强度较优的纱线,其中,以减小纤维线密度(B)为主,即增加纱线中纤维根数最为有效.
对比表3和4可以发现,各自变量对因变量的直接影响效果较总影响效果有波动.这是由于表4呈现的各项指标是排除其他变量干扰后对棉纱强度的直接作用,反映了单因素比较真实的影响情况.由表4可以看出,单因素对棉纱强度的影响为马克隆值(E)最大,其后依次为纤维线密度(B)、纱线线密度(G)、纤维主体长度(C)、纤维强度(A)、纱线捻度(H)、短绒率(D)、纤维基数(F).自变量对因变量的直接影响可以用来定量分析纤维各项性能指标对纱线强度的实际影响,去除了纤维指标间由于相关性产生的抵消作用,而这种负作用即表现为各项指标对棉纱强度的间接影响,影响效果如表5所示.其中,马克隆值(E)的间接影响比较明显,由于对棉纱强度间接影响的存在,其对棉纱强度的实际影响减弱.

表3 标准化后各自变量对因变量影响的总效果Table 3 Standardized total effects of each independent on dependent variables

表4 标准化后各自变量对因变量影响的直接效果Table 4 Standardized direct effects of each independent on dependent variables

表5 标准化后各自变量对因变量影响的间接效果Table 5 Standardized indirect effects of each independent on dependent variables
4 结 语
本文采用路径分析方法,对棉纱强度的影响因素进行定量分析,研究结果与传统的定性相关分析一致.路径分析假设模型将棉纤维主体长度、断裂强度、线密度、马克隆值、短绒率、基数这6项纤维性能指标以及纱线线密度、捻度2项工艺指标对棉纱强度的影响分解为直接效应和间接效应,可以明显地发现多个因素间彼此信息受到掩盖的程度,揭示各指标直接作用于纱线强度的具体情况,从而为配棉及工艺设计中更有针对性地对各指标进行关注提供参考.
[1] ABDEL S,SOURADY E L,ORLEY S W,et al.The relative contribution of fiber properties to variations in yarn strength in upland cotton,groddypium hidrsutum [J].Text Res J,1974,44(4):301-305.
[2] LOUIS A F,JOHN J B,JACK E S.Effect of cotton fiber strength on single yarn properties and on processing behavior [J].Text Res J,1954,24(6):503-507.
[3] GAIN L L,LOUIS A F,JACK E S.Blending cotton differing in fiber bundle break elongation [J].Text Res J,1961,31(5):122-124.
[4] 徐鑫华.基于灰色关联的进口棉花HVI与纱线质量的关联度研究[J].中国制造业信息化,2011,40(13):55-58.
[5] DAYIK M. Prediction of yarn properties using evaluation programing [J]. Text Res J,2009,79(11):963-972.
[6] 吴明隆.结构方程模型:AMOS的操作与应用[M].重庆:重庆大学出版社,2009.
[7] 石爱菊.通径分析方法在苎麻生产实践中的应用[J].南京邮电大学学报:自然科学版,2009,29(1):68-73.
Quantitative Analysis of Indices Influencing on Cotton Yarn Intensity Based on Path Analysis
LIXiao-feng,YUChong-wen
(College of Textiles,Donghua University,Shanghai 201620,China)
Path analysis based on structural equation modeling was adopted for quantitative analysis to the factors which have an influence on cotton yarn intensity.Data of6 fiber performance,such as main length,breaking strength,fineness,micronaire value,short fiber content,length uniformity in a certain range of fiber,and 2 technology index,including yarn linear density and twist,were changed,then,total effect,direct effect and indirect effect of them on the yarn intensity were discussed.The research result showed that the influence of 8factors on the yarn intensity was in accord with the result of qualitative analysis.Path analysis provides a comprehensive quantitative express about direct and indirect effect of each index to yarn intensity,moreover,the degree of influence is observed from it,which is helpful to the selection of cotton fiber performance and the value of correlative technology before the yarn is produced.
cotton yarn intensity;structural equation modeling;path analysis;path coefficient;correlation analysis
1671-0444(2015)01-0032-05
2014-04-11
李晓峰(1980—),女,黑龙江大庆人,博士研究生,研究方向为智能算法在棉纺系统上的应用.E-mail:lxf_8022@mail.dhu.edu.cn
郁崇文(联系人),男,教授,E-mail:yucw@dhu.edu.cn
TS 101.2
A
