基于邻域信息的社区发现方法

韩路，张海

(西北大学数学学院，陕西 西安　710127)

基于邻域信息的社区发现方法

韩路，张海

(西北大学数学学院，陕西 西安710127)

考虑含有节点邻域信息的新模块度函数的社区发现方法和最优分组下标度参数的选择问题，通过谱松弛方法求解模块度函数的最大化问题，最终利用新算法快速求解，并通过真实网络数据验证算法能更好的发现社区.

模块度函数；邻域信息；谱方法

1　前言

复杂网络作为一种数据关系的表达方法，成为目前机器学习领域的热点之一.其中，网络中的节点表示研究问题的对象，边表示对象和对象之间的一种属性关系.在现实世界中，复杂网络常分为以下几种类型，如技术网络，社交网络，信息网络和生物网络等[1-2].社区描述网络的结构，它是指在一个较大的网络中，网络的结构特征通过节点位于不同组表现出来.比如组内边的联接比较紧密，组间边的联接比较稀疏.如何有效发现网络中的社区，对于理解网络功能和结构有着重要意义.例如，在一个学术关系网络中，节点表示作者，边表示每两位作者之间是否有合作发表论文.此网络中的社区可能由一些研究方向相同或相近的作者组成，形成不同特征的社区.因此，如何发现此类社区并预测网络中某一位作者所属的社区，对于研究网络的行为具有实际意义.近年来，社区发现是网络研究的热点之一[3-4].

Newman和Girvan[5]第一次提出模块度函数Q用于社区发现.尽管模块度函数自提出后得到广泛应用，发展了很多以该函数为目标函数的新算法.如Newman[6]提出的一种贪婪策略下的快速聚合算法，White和Smyth[7]提出的一种谱聚类方法等.但是该函数Q并没有利用节点的邻域信息，对于很多有节点信息的真实网络，则该模块度函数Q并不能很好地度量该网络的社区结构.因此，研究结合节点信息的社区发现方法有着重要意义.而文献[8]利用了节点的邻域信息，扩展并提出了新的模块度函数QDist，它度量了节点的邻域信息，QDist不但适合节点有额外信息的网络，而且可以得到不同标度下的社区结构.虽然该文章给出了在特定标度下的最优分组结果，但是并没有给出如何选取此标度的方法.通常地，基于模块度函数方法发现社区有许多典型的算法，如何利用并推广现有算法到结合了节点信息的新模块度函数发现社区，同时如何选取最优分组时的标度是本文关注的问题.

谱分析方法早在20世纪70、80年代就已经被提出[9]，该方法后来被发展成许多不同的谱聚类方法[10].其基本思想是通过对邻接矩阵形成的拉普拉斯矩阵或者标准拉普拉斯矩阵的特征值与特征向量进行分析，从而进行网络的社区发现.而Newman[11-12]将谱分析方法与模块度函数最大化相结合，提出一种谱方法并应用于社区发现.

本文研究将Newman所提出的谱方法推广到新的模块度，同时解决新模块度函数最优分组时标度参数的选择问题.通过将最大化QDist问题转化为谱松弛问题，进而提出一种二分的谱算法，同时给出了最优分组时标度的选取方法.最后，通过在三个真实网络数据上进行实验，结果表明该算法能够有效的给出实际网络二分的社区结构.

2　模块度函数 QDist最大化及算法

一个网络通常包括两组信息，节点个数n和邻接矩阵A=(Aij)1≤i，j≤n.其中，Aij取值为1或者0.当Aij=1时，表示节点i和j之间有边连接，当Aij=0时，表示节点i和j之间没有边连接.模块度函数的定义如下：

上述三种距离分别描述两节点之间的联接强度，不同距离的选择包含网络中不同的结构信息.例如，Jaccard距离[13-14]包含网络的节点的邻域信息，欧式距离包含网络的节点的属性信息，最短距离包含网络的拓扑信息.

一般地，对于一个网络，当知道网络的真实分组时，可以计算QDist的值，并且QDist的值越大，社区结构越明显.本文仅考虑无向网络的两分社区情况，使得QDist最大化.对于节点i，若si的值为1，则表示节点i属于组1，若si的值为−1，则表示节点i属于组2，那么δ(li，lj)可以化为(sisj+1)/2.则

3　实验

本节通过对真实数据Zachary空手道俱乐部网络，海豚社交网络和美国政治书籍网络试验说明算法的有效性.本实验中的相似距离 dij都采用 Jaccard距离.即这里Γ(i)表示节点i的邻居节点.

实验一本实验通过对 Zachary空手道俱乐部网络[15]进行实验，该网络是 Zachary 在1970年代初，研究了一所美国大学的空手道俱乐部成员的社交网络.网络中的节点代表34位俱乐部成员，边代表每个成员之间的友谊关系.但是由于在是否涨学费问题上的分歧，俱乐部主席(节点34)和教练(节点1)的之间发生了冲突，俱乐部自发形成了支持管理者和教练的两组成员.不同的分组按红色和蓝色区分.现在的问题是在只知道邻接矩阵的情况下，能否正确检测出空手道俱乐部网络真实的社区结构？本实验参数ε=10−3.

实验分析图1(b)表示空手道俱乐部网络在利用本文算法得出分组的QLaplace值的情况，当σ∈(0，0.20)和σ=1.04时，网络的分组结果如图1(a)所示，由图1(b)可知，此时网络的分组的QLaplace值最高(忽略了0值，因为此时的分组是全部节点分成一组)，和真实分组比较，除了节点3与真实网络分组不同之外，其他节点的分组完全相同.

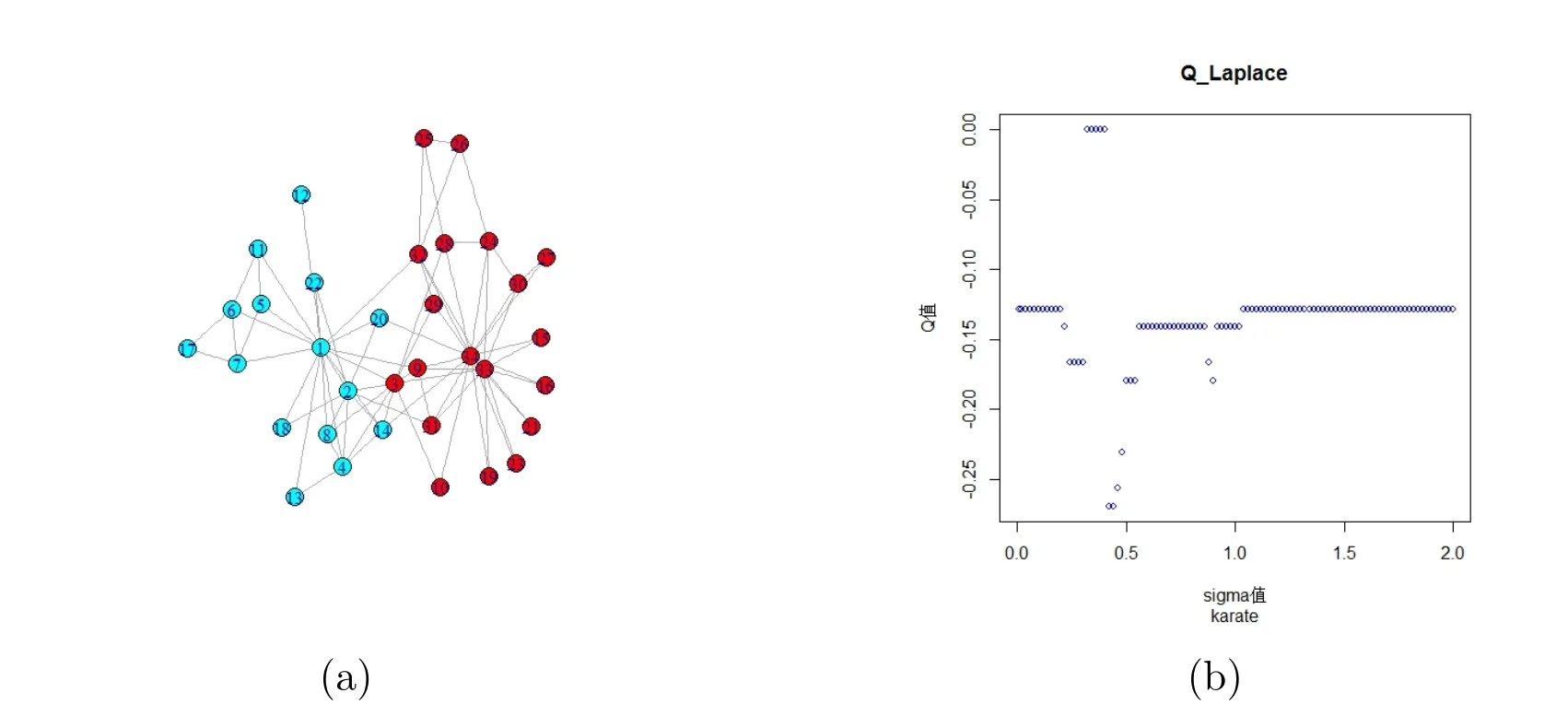
图1　空手道俱乐部网络

实验二本实验通过对海豚社交网络[16-17]进行实验，该网络是Lusseau在神奇湾观察62只海豚后建立的.网络中的节点代表62只海豚，如果两只海豚之间有边，则表示这两只海豚被观察在一起次数多于期望的次数，代表海豚之间某种亲密关系.但是由于一只海豚的暂时离开导致海豚群体分成了20只和 42只两个组.不同的分组按红色和蓝色区分.本实验参数ε=10−3.

实验分析图 2(c)表示海豚社交网络在利用本文算法得出分组的 QLaplace值的情况. 当σ∈(0，0.34)和σ∈(0.72，+∞)时，网络的分组结果如图2(a)所示.和真实分组比较发现，除了节点31和节点40与真实网络分组不同之外，其他节点的分组完全相同.当σ=0.4时，网络的分组情况如图2(b)所示，由图2(c)可知，此时网络分组的QLaplace值最高(忽略了0值，因为此时的分组是全部节点分成一组)，和真实分组比较发现，只有节点40和真实网络分组不同，此时的分组结果比其他QLaplace值的结果都要好.

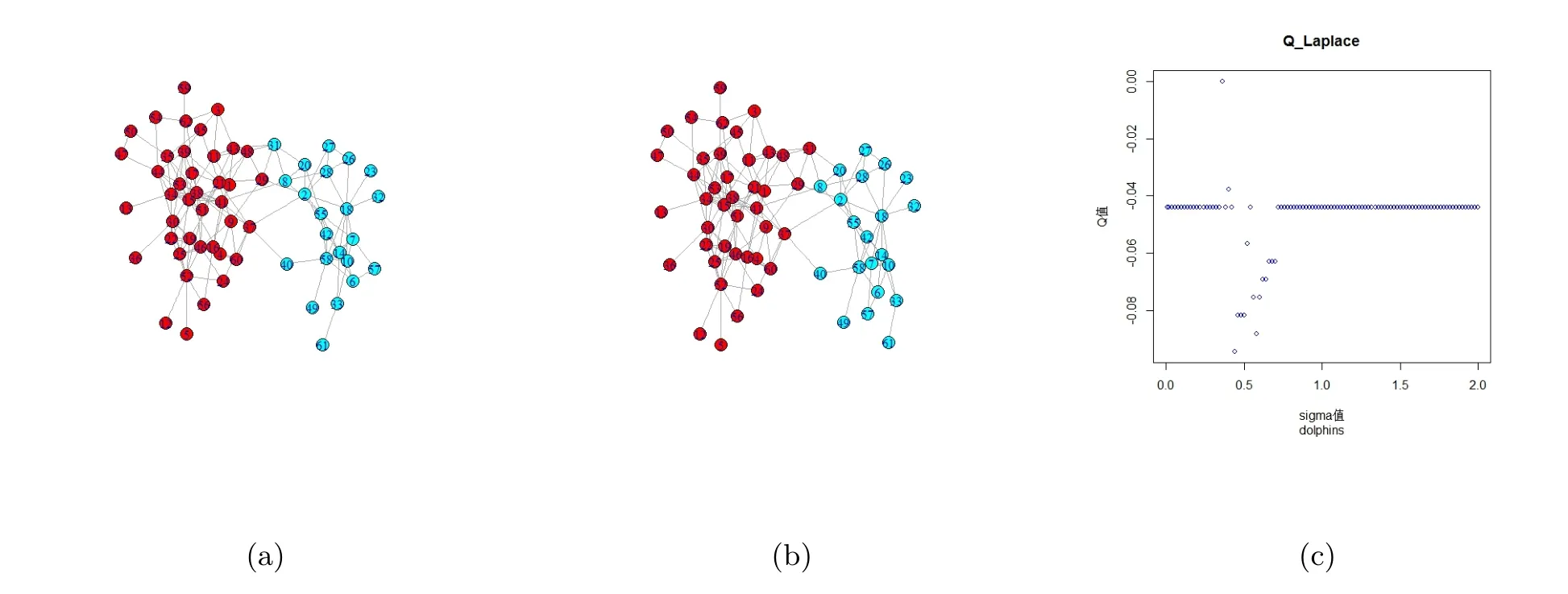
图2　海豚社交网络

实验三本实验通过对美国政治书籍网络进行实验.该网络节点表示在亚马逊网站销售的105本关于美国政治的书籍，边表示两本书经常被同一消费者购买.该书籍被Mark Newman划分为关于自由党和保守党两种书籍，还有少部分书籍被划分为中间派书籍.不同的分组按红色和蓝色区分.本实验参数ε=10−2.

实验分析图3(c)表示美国政治书籍网络在利用本文算法得出分组的QLaplace值的情况. 当σ∈(0，0.32)和σ∈(1.34，+∞)时，美国政治书籍网络的分组结果如图3(a)所示.该结果将节点59和节点78错分.但是当σ∈(0.88，1.06)时，该网络分组结果如图3(b)所示.由图3(c)可知，此时网络分组的QLaplace值最高，该结果同图3(a)的结果相比较，节点53的分组结果不同.此时把节点53错分.节点53的5个邻居节点中有3个被分为自由党，2个被分为保守党，所以将节点53错分了.

4　结论

本文研究了网络的社区结构问题，通过将包含邻域信息的模块度函数QDist的最大化问题转化为谱松弛问题，同时提出一种二分的谱算法进行求解.将Newman的二分谱方法推广到新模块度函数模型上，同时解决的新模块度函数下网络最优分组时的标度选取问题.最后，通过实验证明了新算法可以有效的辨识网络的二分社区结构.

[1]Newman M E J.Networks：An Introduction[M].New York：Oxford University Press，2010.

[2]Albert R，Barabsi A.Statistical mechanics of complex networks[J].Reviews of Modern Physics，2002，74：47-97.

[3]Newman M E J.The structure and function of complex networks[J].SIAM Review，2003，45：167-256.

[4]Newman M E J，Leicht E.Mixture models and exploratory analysis in networks[J].Proceedings of the National Academy of Sciences，2007，104：9564-9569.

[5]Newman M E J，Girvan M.Finding and evaluating community structure in networks[J].Phys.Rev.E.，2004，69：026113.

[6]Newman M E J.Fast algorithm for detecting community structure in networks[J].Phys.Rev.E.，2004，69：066133.

[7]White S，Smyth P.A spectral clustering approach to finding communities in graphs[J].In：Kamath C，Goodman A，eds.Proc.of the 5th SIAM Int Conf.on Data Mining.Philadelphia：SIAM，2005，76-84.

[8]Liu X，Murara T，Wakita K.Extending modularity by capturing the similarity attraction feature in the null model[J].2013，arXiv：1210.4007 v3[cs.SI].

[9]Fiedler M.Algebraic connectivity of graphs[J].Czech Math J.，1973，23(98)：298-305.

[10]Von Luxburg U.A tutorial on spectral clustering[J].Statistics and Computing，2007，17：395-416.

[11]Newman M E J.Modularity and community structure in networks[J].Proc.Natl.Acad.Sci.USA，2006，103(23)：8577-8582.

[12]Newman M E J.Spectral methods for network community detection and graph partitioning[J].Phys.Rev. E.，2013，88：042822.

[13]Levandowsky M，Winter D.Distance between sets[J].Nature，1971，234：34-35.

[14]Jaccard P.Etude comparative de la distribution florale dans une portion des alpes et des jura[J].Bull.Soc. Vaudoise Sci.Nat.，1901，37：547-579.

[15]Zachary W W.An information flow model for conflict and fission in small groups[J].Journal of Anthropological Research，1977，33：452-473.

[16]Lusseau D.The emergent properties of a dolphin social network[J].Proceedings of the Royal Society of London Series B，2003，270：S186-S188.

[17]Lusseau D，Schneider K，Boisseau O J，et al.The bottlenose dolphin community of doubtful sound features a large proportion of long-lasting associations[J].Behavioral Ecology and Sociobiology，2003，54：396-405.

Community detection based on neighborhood information

Han Lu，Zhang Hai
(College of Mathematics，Northwest University，Xi′an710127，China)

Community detection based on modularity is a widely used method，but it does not use neighborhood information of nodes，then it fails to be a good representation of real-world community structure.A new modularity with neighborhood information could detect the community structure of real-world networks，but it didn’t show parameter selection of the best community division.The paper aimed at the maximization and parameter selection of the new modularity with neighborhood information，then reformulate the maximization as a spectral relaxation issue.Finally，we solve the problem by a new bisection spectral algorithm and prove the effectiveness of our algorithm by experimental results.

modularity，neighborhood information，spectral method

O233，TP391.41

A

1008-5513(2015)01-0085-08

10.3969/j.issn.1008-5513.2015.01.010

2014-11-05.

国家自然科学基金(11171272).

韩路(1990-)，硕士生，研究方向：机器学习.

2010 MSC:91D30