一类锥约束多目标优化问题的高阶对偶研究

李红梅，高英

(重庆师范大学数学学院，重庆　400047)

一类锥约束多目标优化问题的高阶对偶研究

李红梅，高英

(重庆师范大学数学学院，重庆400047)

在一类锥约束单目标优化问题的一阶对偶模型基础之上，建立了锥约束多目标优化问题的二阶和高阶对偶模型.在广义凸性假设下，给出了弱对偶定理，在Kuhn-Tucker约束品性下，得到了强对偶定理.最后，在弱对偶定理的基础上，利用Fritz-John型必要条件建立了逆对偶定理.

锥约束多目标优化；广义凸；对偶定理

1　引言

对偶理论是多目标优化问题的主要研究内容.1961年，Wolfe[1]首次利用Kuhn-Tucker最优性条件，在凸性假设下建立了一阶对偶模型并证明了弱对偶定理.随后，为了减弱凸性假设条件，Mond和Weir[2]提出了另一种一阶对偶模型，并在伪不变凸和拟不变凸假设下给出了弱对偶定理.1975年，Mangasarian[3]在一阶Wolfe型对偶的基础上通过引进二次可微函数，建立了二阶和高阶对偶模型.Mond和Weir[2]考虑了另一种二阶对偶模型(Mond-Weir型对偶模型).随后，许多学者开始研究各种二阶和高阶对偶模型[4-9].

1996年，Nanda和Das[10]考虑了如下锥约束问题(NP)：

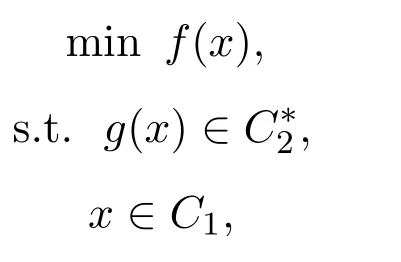
其中f：S→R，g：S→Rm，f，g分别是二次可微函数.S∈Rn是闭集且C1，C2是Rn和Rm内的非空凸锥.C∗2为C2的负极锥.

Nanda和Das[10]建立了问题(NP)的四种对偶模型，在伪不变凸和拟不变凸的假设之下给出了弱对偶定理.随后，Chandra和Abha[11]对四种模型进行了修正，并在广义凸性假设下证明了四种对偶模型的弱对偶和强对偶定理，但并没有给出其逆对偶定理.因此，文献[12]中利用Fritz-John型必要条件给出了四种对偶模型的逆对偶定理.

本文是在文献[12]的基础之上，考虑了多目标锥约束优化问题的二阶和高阶对偶模型，给出并证明了相应的弱对偶，强对偶和逆对偶定理.本文结构如下：第1节，给出了一些基本知识以及锥约束多目标优化问题高阶对偶模型.第2节，讨论了锥约束多目标优化问题高阶对偶模型的弱对偶，强对偶和逆对偶定理.第3节，给出了锥约束多目标优化问题的二阶对偶模型并讨论了其弱对偶，强对偶和逆对偶定理.

2　预备知识

设Rn是n维欧氏空间，Rn+是非负象限.对x，y∈Rn给出以下符号：

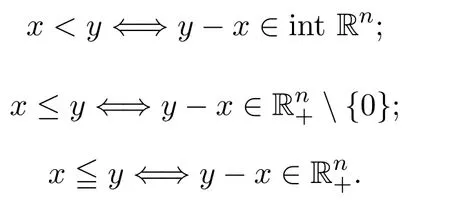
定义2.1[13]设S⊂Rn是闭集，函数f：S→R在S上关于η是高阶伪不变凸的，如果对任意x，u，p∈S，有

定义2.2[13]设S⊂Rn是闭集，函数f：S→R在S上关于η是高阶拟不变凸的，如果对任意x，u，p∈S，有

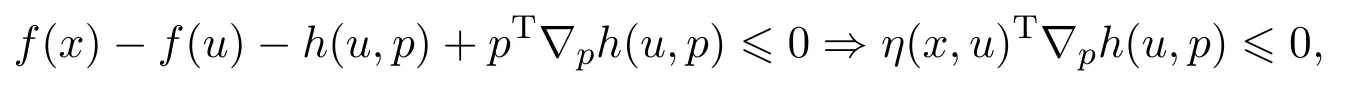
其中函数η：S×S→Rn，函数h：S×Rn→R且h关于p可微.

定义2.3[14](i)可行解称为问题(MOP)的弱有效解，若不存在x∈S使得

对于(MOP)，在文献[11]中锥约束单目标对偶模型(D)2的基础之上，建立如下高阶对偶模型(HD)：

其中，h：Rn×Rn→Rl和k：Rn×Rn→Rm是二阶连续可微函数.

3　高阶对偶定理

下面将讨论弱对偶定理，强对偶定理和逆对偶定理.

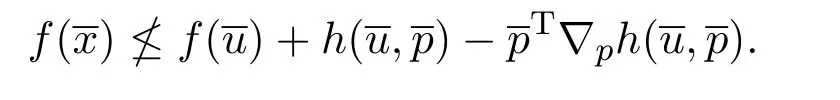
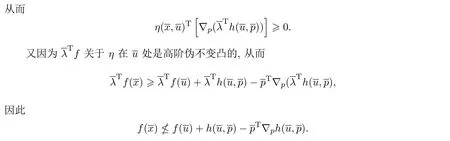
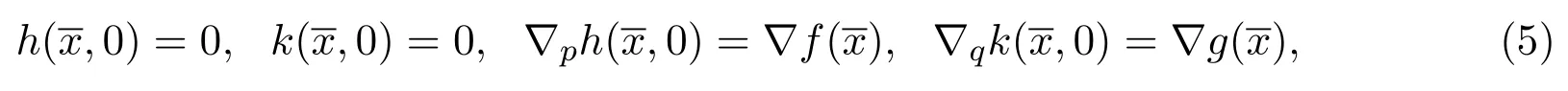
4　二阶对偶定理

下面讨论问题(MOP)的高阶对偶模型(HD)的特殊情况.令

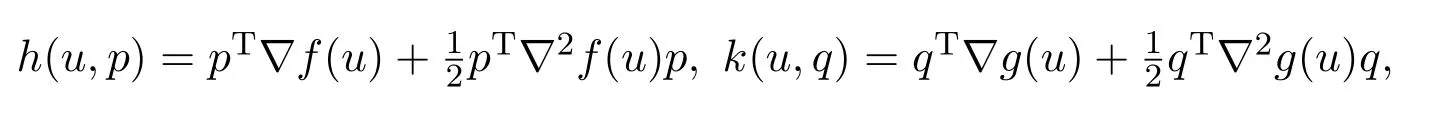
则高阶对偶(HD)退化为(MOP)的二阶对偶模型(SD)：

注4.1当h(u，p)=pT∇f(u)，k(u，q)=qT∇g(u)，l=1时，多目标高阶对偶模型(HD)退化为文献[6]中的单目标一阶对偶模型(ND)2.

高阶对偶模型(HD)的弱对偶定理3.1和强对偶定理3.2可分别退化为二阶对偶模型(SD)的弱对偶和强对偶定理.

下面给出例子说明逆对偶定理的合理性.

正定且−yg(0，0)=0.因此定理4.3中的假设条件都满足，故(0，0)是(MOP)的可行解.又因(λ，u，y，p=0，q=0)满足定理4.1中的广义凸性假设条件，因此(0，0)是(MOP)的有效解.

事实上，原问题只有(0，0)一个可行解，因此(0，0)确实是原问题(MOP)的有效解.

[1]Wolfe P.A duality theorem for nonlinear programming[J].Quart.Appl.Math.，1961，19：239-244.

[2]Mond B，Weir T.Generalized Concavity and Duality，in：S.Schaible，W.T.Ziemba(Eds)，Generalized Concavity in Optimization and Economics[M].New York：Academic Press，1981.

[3]Mangasarian O L.Second and higher-order duality in nonlinear programming[J].J.Math.Anal.Appl.，1975，51：607-620.

[4]Gulati T R，Divya Agarwal.On Huard type second-order converse duality in nonlinear programming[J]. Appl.Math.ett.，2000，20：1057-1063.

[5]Yang X M，Yang X Q，Teo K L.Higher-order generalized convexity and duality in nondifferentiable multiobjective mathematical programming[J].J.Math.Anal.Appl.，2004，297：48-55.

[6]Yang X M，Yang X Q，Teo K L.Huard type second-order converse duality for nonlinear programming[J]. Appl.Math.Lett.，2005，18：205-208.

[7]Ahmad I，Husain Z，Sarita Sharma.Higher-order duality in nondifferentiable multiobjective programming[J]. Numerical Functional Analysis and Optimization，2007，28：989-1002.

[8]高英.一类多目标广义分式规划问题的最优性条件和对偶[J].纯粹数学与应用数学，2011，27(4)：476-485.

[9]高英.非可微多目标优化问题的高阶逆对偶定理[J].纯粹数学与应用数学，2014，30(2)：136-142.

[10]Nanda S，Das L N.Pseudo-invexity and duality in nonlinear programming[J].European Journal of Operational Research，1996，88：572-577.

[11]Chandra S，Abha.A note on pseudo-invex and duality in nonlinear programming[J].European Journal of Operational Research，2000，122：161-165.

[12]Yang X M，Yang X Q，Teo K L.Converse duality in nonlinear programming with cone constraints[J]. European Journal of Operational Research，2006，170：350-354.

[13]Mond B，Zang J.Higher order invexity and duality in mathematical programming[J].European Journal of Operational Research，1998，163：357-372.

[14]Sawaragi，Yoshikazu Date.Theory of Multiobjective Optimization[M].Japan：Department of Applied Matheatics Konan Uinversity，1985.

Higher-order duality in multiobjective programming problems with cone constraints

Li Hongmei，Gao Ying

(Department of Mathematics，Chongqing Normal University，Chongqing400047，China)

In this paper，basing on the first-order dual models for single objective problems with cone constraints，we construct second-order and higher-order dual models for nonlinear multiobjective programming problems with cone constraints.And then we establish weak and strong duality theorems under generalized convexity assumptions.By using Fritz-John type necessary condition，converse duality theorems are established.

multiobjective programming problems with cone constraints，generalized convexity，duality theorems

O221.6

A

1008-5513(2015)01-0073-12

10.3969/j.issn.1008-5513.2015.01.009

2014-07-18.

国家自然科学基金(11201511)；重庆市重点实验室专项项目(CSTC，2011KLORSE03).

李红梅(1988-)，硕士生，研究方向：多目标规划.

2010 MSC:90C32，90C46，90C47