基于改进的离群点检测软测量方法研究

付晓幸 于佐军



基于改进的离群点检测软测量方法研究

付晓幸 于佐军

（中国石油大学（华东）信息与控制工程学院）

提出一种改进的离群点检测方法，采用参数更新的支持向量数据描述的离群点检测方法，并引入贝叶斯分类原理对离群点分类，对校正离群点后的数据用最小二乘支持向量机建模并预测。工业聚丙烯熔融指数软测量模型的应用结果表明：该方法预测精度更高，泛化能力更强。

软测量；离群点检测；贝叶斯分类

0　引言

石油、化工等工业生产过程中，为确保产品的质量和生产过程持续稳定，关系到产品质量的过程变量需要被实时控制和监测[1]。但是实际生产过程中大量过程变量难以用传感器直接检测甚至无法检测，例如航空煤油干点、纸浆的Kappa值以及聚合反应中聚合物的熔融指数等。软测量技术应运而生。

软测量技术的核心是软测量模型的建立[2-3]。在目前软测量建模中，基于数据的统计建模占主导地位。由于测量仪表自身故障和传感器容易受化工环境影响，使测量数据偏离原来范围，导致离群点产生，而离群点对软测量模型的预测精度影响很大，因此需要排除离群点。生产过程中生产过程切换或物料改变会产生不同于历史采集的数据，易被误判成离群点排除。如何确定离群点是由干扰产生，还是由过程变化引起，已成为软测量技术研究的重点。

为解决上述问题，Wang Jin等[4]提出一种在线离群点检测和分类的自适应软测量，该方法先以故障检测PCA算法中的SPE指标作为离群点判断的准则，再把检测出的离群点进一步进行判断。Galicia H等[5]在控制过程应用中，提出一种贝叶斯方法检测离群点并对其分类。如何鉴别工业生产过程采集样本数据的离群点，并判断其是否为真正意义上的离群点，仍没有通用的方法。

针对上述问题，本文引入基于支持向量数据描述（support vector data description，SVDD）的离群点检测方法，对化工运行过程中存在的离群点进行检测。为判断离群点是否为真正意义上的离群点，提出离群点分类的概念。基于贝叶斯分类原理把离群点分为脉冲型离群点、短阶跃型离群点和长阶跃型离群点。其中脉冲型和短阶跃型是真正意义上的离群点需要排除校正，而长阶跃型代表化工过程的变化。对需要校正的离群点采用时间序列校正的方法进行校正后用最小二乘支持向量机（least square support vector machine，LSSVM）建模。

1　离群点检测方法

1.1SVDD算法

Tax等人提出SVDD是解决单值分类问题的有效方法，是一种基于支持向量机学习的算法[6]。单个值分类要解决的问题是区分目标类的数据和其他所有不属于目标类的数据（称为异常类）。支持向量数据描述可以将目标数据建立支持向量数据描述模型，包括目标数据超领域、与所有异常类的目标类。输入的空间不可分离，通过一个非线性映射函数，把数据从输入空间映射到一个高维空间，寻找支持向量在特征空间中构造包围与最小半径和超球体的最佳点。

(1)

(3)

把式(2)表示为对偶问题，并引入核函数取代特征空间上的内积运算得

(4)

SVDD算法在不使用类标的情况下，解决了单值分类问题，通过引入惩罚参数，使在训练数据中包含噪声的条件下SVDD算法仍能工作。

1.2改进的支持向量数据描述参数更新

模型在实际运行中，如果发生过程变化，如汽油干点软测量中精馏塔的原油发生变化，则测量数据会超出检测判断的正常范围。SVDD的参数半径和球心应随着数据的变化而变化，这样才能适应过程的变化而不会导致误判正常数据为离群点[7]。针对这个过程引入了指数加权移动平均（EWMA）鲁棒的方式更新SVDD参数，指数加权移动平均的公式如下：

(6)

2　离群点分类方法

2.1朴素贝叶斯理论

贝叶斯分类器是一种基于统计方法的典型分类模型，它基于贝叶斯理论，先验概率和后验概率被巧妙地联系在一起，利用先验信息和样本数据来确定所述事件的后验概率[8-9]。

(7)

(8)

2.2改进的基于朴素贝叶斯的离群点分类算法

为判断离群点是否为真正意义上的离群点，采用贝叶斯分类原理对已检测到的离群点进一步分类。

2.2.1长阶跃数据的判断准则

对于一个阶跃干扰，通过计算每个Post-Change Window中的联合后验概率来确定后验概率的模式。因为，所以对每个子集，阶跃幅值可用的均值表示

假设所有的数据都服从高斯分布，则正常状态下和发生阶跃后的概率密度函数分别用和表示。所以，发生阶跃时任意离群点的似然函数表示为

(10)

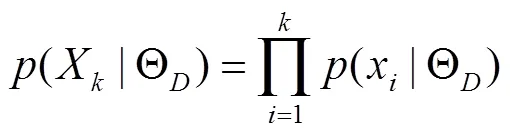
把式(10)代入式(11)，得

(12)

因此，用式(8)计算的联合后验概率变为

(14)

假设干扰的类型是阶跃，则在Post-Change Window中第一个数据点的后验概率是

(16)

仅依靠式(17)无法判断此时发生的阶跃是否为长阶跃。因此，还需要Post-Change Window中更多的数据来证明。由于假设阶跃发生在Post-Change Window的开始，所以随着样本数目的增加，后验概率也单调递增

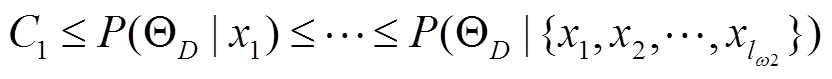
为提高对长阶跃信号检测和分类的精确性，需让整个Post-Change Window的后验概率比置信限大

(18)

2.2.2脉冲数据的判断准则

对于脉冲信号的干扰，在Post-Change Window中的第一个值提供了脉冲信号的幅值，而阶跃信号需要很多数据才能确定。因此，对于脉冲干扰，要确定脉冲干扰，首先需满足式(16)，其中，为置信限，满足分布。

2.2.3短阶跃数据的判断准则

假设干扰是短阶跃，在Post-Change Window中短阶跃持续阶段的后验概率必须满足和长阶跃一样的关系：

与式(19)一样，在Post-Change Window中短阶跃持续阶段的后验概率必须大于1个置信限

(21)

为了识别短阶跃干扰结束，在Post-Change Window后的短阶跃的后验概率必须小于一个阈值：

式(20)~式(22)就是判断短阶跃的准则。

具体分类过程如图1所示。

图1　贝叶斯对离群点的分类过程

3　仿真研究

聚丙烯以其良好的应用性能越来越受到人们的关注，成为全球发展最迅速的热塑性材料。本文以某石化企业聚丙烯生产装置采用的Spheripol工艺技术为例进行仿真。数据来源为某石化公司在2007年8月~12月间，聚丙烯的生产过程数据[10]。结合现场操作中的实际经验和机理分析的结果，选定用于建立聚丙烯熔融指数软测量的辅助变量有：第一环管反应器R201中丙烯的浓度、氢气的浓度、催化剂的浓度；第二环管反应器R202中丙烯的浓度、氢气的浓度、催化剂的浓度以及总的宏观反应热。现场采用DCS系统，每20 s采集一次数据，而化验数据每4 h一次，经过时序匹配等处理后得到379组数据，其中229组用来建模，150组用来测试。

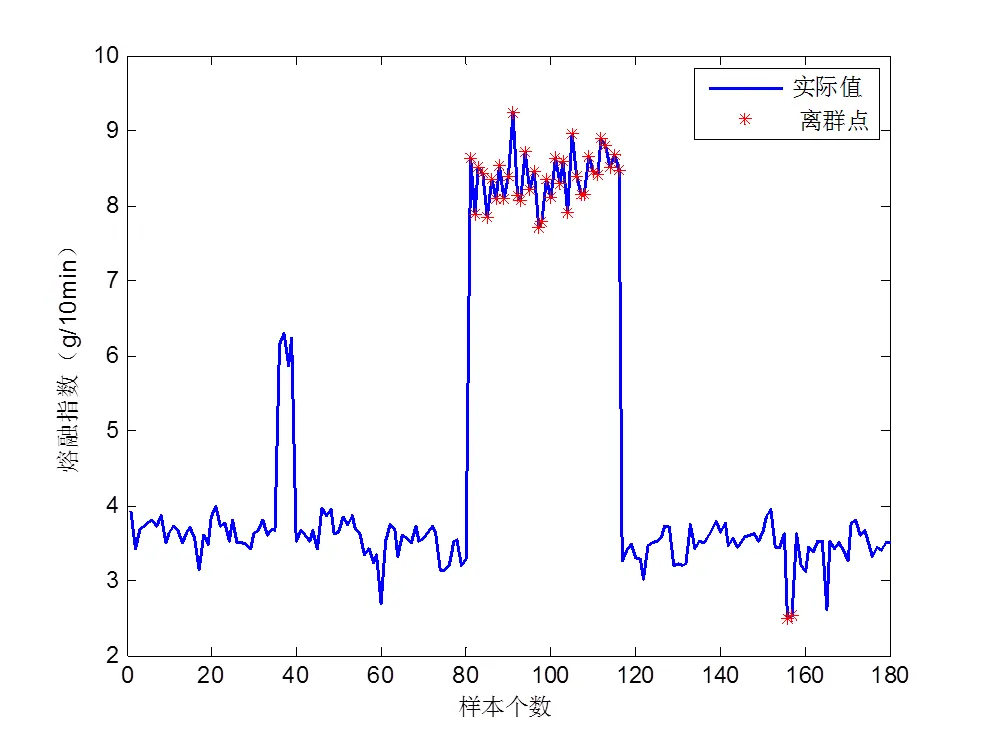
图2　熔融指数的离群点检测

表1 两种离群点检测方法性能对比

当过程发生变化，数据偏离原来的中心范围时被判为离群点，因此离群点的参数更新才不会被误判，而不能实现参数更新。在短阶跃型离群点判别前，根据聚丙烯熔融指数的先验知识规定1个离群点为脉冲型离群点；连续2~15个离群点为短阶跃型离群点；连续15个以上的离群点表示过程切换。所以，用来测试的180组数据的第37~40组数据规定为短阶跃型数据。没有参数更新和分类的SVDD离群点检测的仿真结果如图3所示，有参数更新和分类的SVDD离群点的仿真结果如图4所示。

图4　有参数更新和分类的SVDD离群点检测

由图3和图4可知，本文所提出的离群点分类方法可行，能够很好地判断出离群点的类型。针对不同类型的离群点采取不同的方法来处理，用时间校正方法的自回归移动平均模型对离群点进行校正，校正后的仿真结果如图5所示。

图5　聚丙烯熔融指数离群点校正的曲线

校正数据时没有对过程变化引起的数据进行校正说明本文提出的离群点分类算法起了很好的效果。对离群点校正前和校正后的数据用LSSVM建模。图6和图7分别为两种情况的预测曲线，表2列出了2种方法的泛化误差。

图6　离群点校正前的熔融指数预测曲线

图7　离群点校正后的熔融指数预测曲线

表2　模型预测误差比较

由表2中的定量数据可知采用改进后的离群点检测方法处理的数据建模，模型的预测效果更好，泛化能力更强。

4　结论

以聚丙烯熔融指数为研究对象，对本文的离群点检测、分类、校正等方法进行验证，结果表明：所给出的SVDD检测方法能很好地应用在离群点检测中，其中基于Bayesian算法的离群点分类方法较好地对脉冲型离群点、短阶跃型离群点和长阶跃型数据进行区分，用离群点校正后的数据建模提高了模型的预测精度。

参考文献

[1] 吴长江.常压蒸馏产品质量与收率预测模型建立与应用[D].大庆:大庆石油学院,2008.

[2] 俞金寿,刘爱伦,张克进.软测量技术及其在石油化工中的应用[M].1版.北京:化学工业出版社,2000:2-7.

[3] 李海青,黄志尧.软测量技术原理及应用[M].北京:化学工业出版社,2000.

[4] Wang Jin, He Q Peter. A Bayesian approach for disturbance detection and classification and its application to state estimation in run-to-run control[J]. IEEE Transactions on Semiconductor Manufacturing, 2007, 20(2): 126-136.

[5] Galicia H, He Q, Wang Jin. Adaptive outlier detection and classification for online soft sensor update[J]. Advanced Control of Chemical Processes, 2012, 8(1):402-407.

[6]Hawkins D M. Identification of outliers[M]. 1980.

[7] 王震.基于距离的离群点检测算法分析与研究[D].重庆:重庆大学,2011.

[8] Pell R J. Multiple outlier detection for multivariate calibration using robust statistical techniques[J]. Chemometrics and Intelligent Laboratory Systems, 2000, 52(1): 87-104.

[9] 赵玉霞,王克如,白中英,等.贝叶斯方法在玉米叶部病害图像识别中的应用[J].计算机工程与应用,2007,43(5):193-195.

[10] 巨稳,田学民.基于混合核函数的OLS软测量建模方法研究[J].石油化工自动化,2011,47(1):31-35.

Soft Sensor Research Based on Improved Outlier Detection

Fu Xiaoxing Yu Zuojun

(College of Information and Control Engineering in the University of Petroleum)

A soft sensor research based on improved outlier detection is proposed and the method of outlier detection based on support vector data description (SVDD) is introduced in this paper. To determine whether the outliers get is authentic, the concept of outlier classification is put forward. The application of industrial polypropylene melt index soft measurement modeling has indicated that method has better prediction accuracy and generalization performance.

Soft Measurement; Outlier Detection; Bayesian Classification

付晓幸，女，1990年生，硕士研究生，主要研究方向：工业过程建模、控制与优化等。E-mail:ymnlfuxiaoxing@126.com

于佐军，男，1960年生，硕士生导师，主要研究方向：工业过程建模、控制与优化等。E-mail:yuzuojun@gmail.com