热端温度对热声发动机性能影响的数值研究

张楷，刘益才，谢海波，王寿川，刘亚强，武曈



热端温度对热声发动机性能影响的数值研究

张楷，刘益才，谢海波，王寿川，刘亚强，武曈

(中南大学能源科学与工程学院，湖南长沙，410083)

建立场协同模型，采用计算流体动力学(CFD)方法，对1/4波长驻波热声发动机进行二维数值模拟研究，分析不同热端温度下系统内声功率的变化情况以及板叠与气体工质间的对流传热特性。研究结果表明：波动压力与体积流率幅值随着热端温度的升高而不断增大，相位差随着热端温度的升高呈下降趋势，特定结构的热声发动机对应使系统声功输出最大的最佳热端温度；随着热端温度的升高，板叠与气体工质间的换热量也不断增大，且发现声功率并不与热流量成正比，板叠存在着固定吸热与放热区域。

热声发动机；相位差；数值仿真；场协同

热声热机以其可靠性高、使用寿命长、绿色环保等特点，成为近年来制冷及低温领域的研究热点。经过最近二三十年的快速发展，热声技术的研究已经取得了许多成果[1−4]。但要更进一步地提高声功转换效率，推进其工程化应用，仍需对其理论进行深入研究。采用CFD数值仿真方法是探究热声转换机理并进一步提高系统性能的重要手段。从余国瑶等[5−6]的研究结果中可以看出采用CFD软件对热声发动机进行数值模拟研究是一个切实有效的研究方法。本文采用CFD数值计算方法对高频驻波热声发动机进行二维轴对称数值模拟，重点研究回热器热端温度对系统声功输出以及回热器传热特性的影响。

1 计算模型

1.1 热声发动机场协同模型

在场协同理论与经典线性热声理论的基础上[7−8]，建立热声发动机的场协同模型。该模型是以声功率为目标函数，从压力场与速度场间的协同情况对热声发动机性能进行分析。

1.1.1 基本控制方程

在驻波热声发动机中，其工作流体可看作是连续介质。热声系统内可压缩的黏性流体，其运动规律满足基本守恒方程。在欧拉坐标系下，其控制方程如下[9]。

连续性方程：

动量方程：

能量方程：

气体状态方程：

式中：，，，c，及分别为温度、压力、密度、比定压热容、动力黏度及导热系数；为速度矢量；为作用于单位体积流体上的体积力；为时间；为黏性耗散函数，表征由于黏性力做功所造成的能量耗散。及的表达式见文献[10]。

1.1.2 控制方程的线性化处理

为求解上述微分方程组，Swift对方程进行了一系列简化，将其从微分方程组转换成代数方程[11]，并基于以下假设对其进行求解：

1) 热声系统内压力振幅远小于其平均压力；

2) 固体为刚性固体；

3) 流体工质的比热容远小于固体比热容；

4) 热声元件的横向长度比声波波长要小得多；

5) 振荡流体的时均质量流为0 kg/s；

6) 不考虑流体的入口效应，且将其看作充分发展的层流。

根据上面假设条件，认为流场中存在沿纵向方向传播的平面波，且通过横截面的时均流为0 kg/s，所有与时间相关的物理量都借助角频率表示，其表达式如下：

式中：为波动量的复数幅值；Re[ ]为复数实部；下标“0”表示时均值，下标“1”表示一阶波动值；i为虚数单位。将上述方程组代入守恒方程组，忽略体积力、耗散项以及2阶以上高阶小量的影响，可得：

1.1.3 线性方程组的求解

由相应假设可知，流体的物性和压力在截面上为均匀分布，因此，可以采用截面积分平均法对方程进行化简，推导出一维方程组的表达式，最终可以用下式表示热声系统的控制方程组：

1.1.4 时均声功流

热声机械中能量间的转换通常是通过能流表现的，热声发动机中热能向声能的转化主要是通过声功流来表现。由于热声机械中各物理量多为波动量，能量流均为2个一阶物理量的乘积(如声功流中的压力与体积流率)，二者的乘积多为2阶小量。这里主要研究其1个周期内的时均值。

声功流为气体工质在垂直于声波传输方向截面上的时均功率，声功流表征其做功能力。它是1个二阶量，可表示为压力和体积流率的乘积在1个周期内的积分平均，其具体表达式如下：

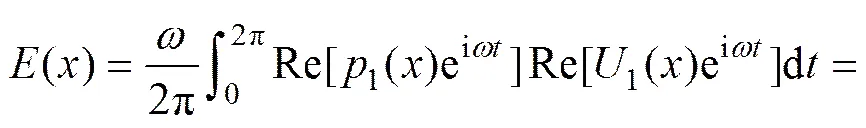
式中：1为截面处波动压力；1为截面处波动体积流率；为1与1间的相位差。从式(15)可以看出：声功流不仅与压力与体积流率的幅值有关，而且与两者间的相位差有关；当压力与体积流率的幅值固定时，声功流则只取决于相位差。特别地，当=90°时，声功流为0 W，即对于纯驻波热声发动机而言，它并不能输出声功。驻波热声发动机有声功输出，因此，它并非纯驻波热声发动机，而是以驻波分量为主混有少量行波分量的混合型热声发动机。驻波热声发动机中压力与体积流率之间的相位差为80°~100°。

从场协同理论[12]可知其基本思想为：当某一特定流体的流速一定时，边界上的热流由速度矢量与温度梯度矢量点乘的积分值来决定。为了提高该积分值来增强换热，需要流体的速度场与温度梯度场有更好的协同性能，而其协同性主要体现在以下3个方面： 1) 尽可能地增大速度矢量与温度梯度矢量的夹角余弦，即让2矢量的夹角尽可能远离90°；2) 在最大流速和温差一定时，尽可能使流体速度和温度均匀分布；3) 尽可能使3个标量场中的大值与大值搭配，也就是说，使3个标量场的大值尽可能同时出现在流场中的某些区域。

对于热声发动机，更关注的是系统输出声功的能力。将式(15)与式(16)中的积分因子进行对比，得出式(17)。之所以将两者放到一起对比，是因为对于对流传热，提高积分因子即可增强对流换热强度。且通过对比可以发现，两者的形式基本一致，即要提高热声发动机的声功输出，不仅需要提高压力与体积流率的幅值，同时也要使两者间的相位差远离90°，即使得压力场与速度场协同性能更好。故借用场协同理论来对热声发动机进行研究是一种新颖有效的研究 方法。

1.2 物理模型

驻波热声发动机主要由谐振管、高温端换热器、板叠回热器及低温端换热器组成。为了使计算更加简化，通过设置适当的边界条件来取代高低温端换热器，在建立的几何模型中省略高、低温端换热器，其结构简图如图1所示。由于本文的几何模型是基于Florian等[13]建立的模型创建的，因此，相关的结构参数也与文献[13]中的一样，具体参数如表1所示。

图1 热声发动机系统结构简图

表1 系统结构尺寸

本文网格采用的是四边形结构性网格。由于板叠区域是热声转换的核心区域，并且其内部的流动与换热特性也是要重点关注的对象[14]，所以，在板叠区域使用相对密集型的网格，而在谐振管其他区域使用相对稀疏的网格，这2部分网格通过边界层网格进行过渡连接。在板叠区域网格横向长度和纵向长度分别为 0.20 mm和0.05 mm，谐振管其他区域横向长度和纵向长度分别为0.40 mm和0.40 mm。经Gambit处理后，网格数为69 300，网格最大扭曲度小于0.45，均符合数值研究的条件。其整体网格如图2所示，网格渐变处局部放大图如图3所示。

图2 整体网格分布图

图3 网格渐变处局部放大图

1.3 边界条件及初始化

本文计算模型中包含了流体区域与固体区域，其中板叠区域为固体区域，谐振管其他区域为流体区域。固体工质采用的材料为不锈钢，气体工质采用的是空气，且气体密度采用的是理想气体模型。谐振管右端壁面为开口端，设置为压力出口，其他壁面设置为绝热边界条件；板叠左端壁面为高温端，边界条件设置为恒定温度，设置了700，750，800，850和900 K共5种温度；板叠右端为低温端，边界条件设置为恒定温度300 K；板叠的上下表面则采用耦合边界条件；各壁面均为无滑移边界。系统内的初始速度为0 m/s，初始压力设置为0 Pa，初始温度设置为300 K。

1.4 解散器与离散格式

计算区域的径向和轴向尺寸相差较大，因此，选择二维双精度求解器；湍流模型采用标准−方程且采用二阶、非稳态计算方法；由于流场处于非稳定流动状态，采用压力隐式分裂算法(pressure implicit split operation，PISO)，压强(pressure)方程采用二阶(second order)差分格式离散，其余方程均采用二阶迎风(second order upwind)差分格式离散；能量方程迭代过程中残差的收敛条件为残差小于等于10−6，连续性方程的残差收敛条件为残差小于等于10−3，其余方程收敛的条件为残差小于等于10−4。为了使计算过程中各方程能够更好地耦合，时间步长为10−5s，每个时间步内执行的最多迭代次数为200。

2 计算结果与分析

2.1 声功分析

图4和图5所示分别为热声发动机系统达到稳定状态后压力和体积流率幅值沿轴线在系统内的分布。由图4可知：压力幅值在谐振管闭口端最大，在开口端接近于0 Pa，随着热端温度升高，压力幅值不断增大。由图5可知：体积流率幅值与压力幅值的分布情况相反，在谐振管闭口端幅值最小为0 Pa，在开口端达到最大，这与文献[15]中的实验结果一致。在板叠区域，由于流道面积缩小使得在该处体积流率突然增大，如图5中凸起部分所示。此外，体积流率的幅值也是随着热端温度的升高而不断增大。这主要是因为板叠两端的温度梯度是热声发动机的驱动力，在冷端温度基本不变时，热端温度越高，板叠两端温度梯度越大，即发动机驱动力越大，使得压力及体积流率幅值增大。

温度/K：1—700；2—750；3—800；4—850；5—900

温度/K：1—700；2—750；3—800；4—850；5—900

图6所示为系统振荡周期及监测面(=25 mm)处波动压力与体积流率的相位差随热端温度的分布。由图6可知：随着热端温度的升高，系统振荡周期并未发生明显变化，这是因为系统振荡频率主要由谐振管的长度所决定。而波动压力与体积流率的相位差则随着热端温度的升高整体呈现下降趋势，当热端温度为700 K和750 K时，其相位角最大，为103.17°；当热端温度为900 K时，其相位角最小，为94.97°。造成相位角减小的原因可能是随着热端温度的升高，板叠与气体工质间的传热速度加快，使得系统内温度分布更易趋于一致，从而减小了传热滞后的时间差。

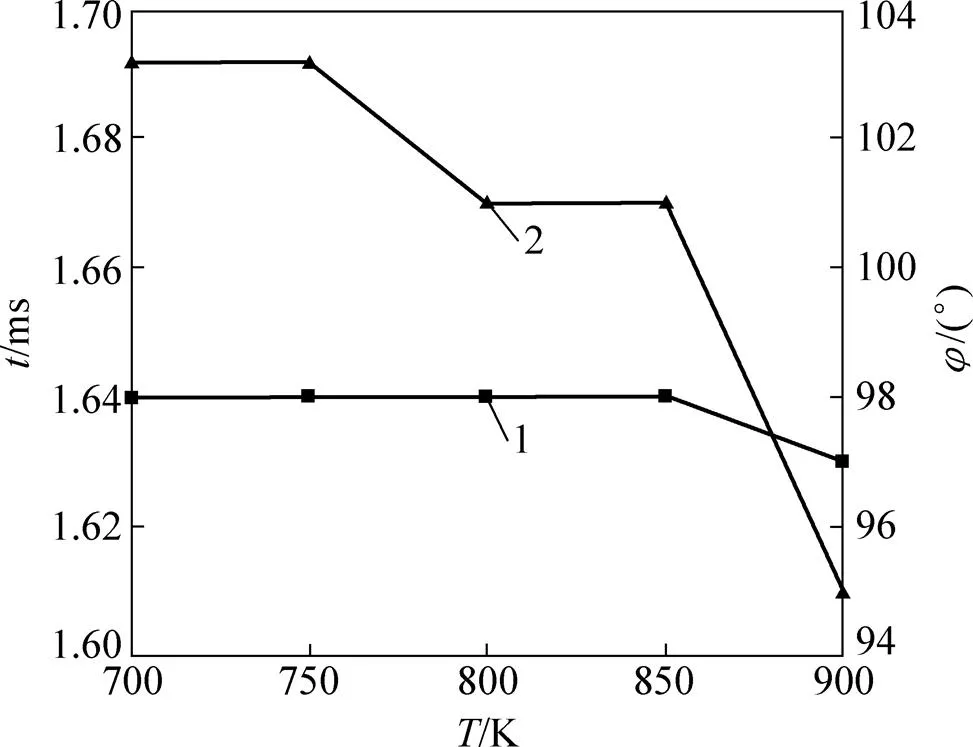
1—t；2—φ

图7所示为监测面处的声功率随热端温度分布。由图7可见：声功率并非随温度升高而单调变化，而是先增大后减小，再增大再减小，在900 K时声功率最小，为76.92 W；在850 K时声功率最大，为 137.81 W；当温度从700 K增加到750 K时，虽然相位角并未发生变化，但由于压力、体积流率幅值有所增大，导致其声功率也有所增大；当温度从750 K增大到800 K时，在压力及体积流率幅值都增大的情况下，声功率反而降低。这主要是因为两者间的相位角减小，压力幅值与体积流率的幅值相对增长量较小，而相位角余弦的相对变化量较大，从而导致声功率降低。当温度从800 K增大到850 K时，由于相位角未发生变化，其声功率的增大仅是压力波动幅值以及体积流率波动幅值增大所致。当温度从850 K增大到900 K时，虽然压力幅值及体积流率幅值都有所增大，但由于相位角急剧减小，从而其声功率也急剧降低，为5种工况中的最小值。所以，对于热声发动机而言，提高热端温度并不一定能提高系统的声功输出，并且对于某种特定的发动机结构存在1个最佳温度，使得系统的声功输出最大。

图7 不同热端温度下的声功率E分布

2.2 传热特性分析

前面讨论了热端温度对系统内声功的影响，而声功能量的主要来源是流体与固体工质间进行的对流传热。下面进一步研究板叠与气体工质间的对流传热特性。

图8所示为板叠与流体工质间的总热流波形分布图，其中正热流表示板叠向气体放热，负热流则表示板叠从气体中吸热。由图8可见：随着热端温度升高，热流量不断增大，并且在1个周期内，板叠放出的热量总是比板叠吸收的要多，这正是热声效应能够发生的1个重要原因。以700 K时的总热流波形图为例，总热流的正向最大值为6.662 kW，而负向最大值仅为6.058 kW，多余的热量就是输出声功的主要能量来源。分析图8还可发现声功的产生并不与换热量成正比。图9所示为压力波形与热流波形分布图。张春萍[16]认为驻波声场中进行的热声转换效应，热声板叠中气体经历的弛豫换热过程，在压力上升过程中吸热，在压力下降过程中放热。由图9可见：压力在上升过程中，大部分时间热流为正，即气体从板叠处吸收热量，而在压力下降过程中大部分时间热流为负，即气体向板叠放热，这与文献[16]中的结果一致。而气体并不是在压力上升的整个过程中吸热，这主要是因为系统中的声场并非纯驻波声场，即两者的相位差并不为90°。

温度/K：1—700；2—750；3—800；4—850；5—900

1—p；2—Φ

为了更进一步了解板叠与内部气体工质间的换热特性，取某一块板叠的上表面为研究重点，考察其在不同时刻板叠表面的热流量分布及流道中心与板叠表面温差分布。选择3个有代表性的时刻：时刻1为总热流量达到正向最大值时所对应的时刻；时刻2为总热流量为0 W时所对应的时刻；时刻3为总热流量达到负向最大值时所对应的时刻。

图10(a)所示为时刻1在不同热端温度下的板叠表面热流量分布，图10(b)所示为板叠表面与流道中心温差(板叠表面温度减去流道中心处的温度)分布。从图10 可以看出：随着热端温度升高，板叠表面的热流量不断增大，并且板叠表面与流道中心处的温差也不断升高。这是由于热端温度越高，其内部流体的流速越快，而该时刻流体是向轴负向流动，低温流体向高温端流动，从而使得其温差加大。通过进一步观察发现：板叠大部分位置(30~38 mm)的温度都比流体温度高，所以，热流图中显示板叠大部分位置都是向流体放热，从而导致本时刻总体表现为板叠向流体 放热。

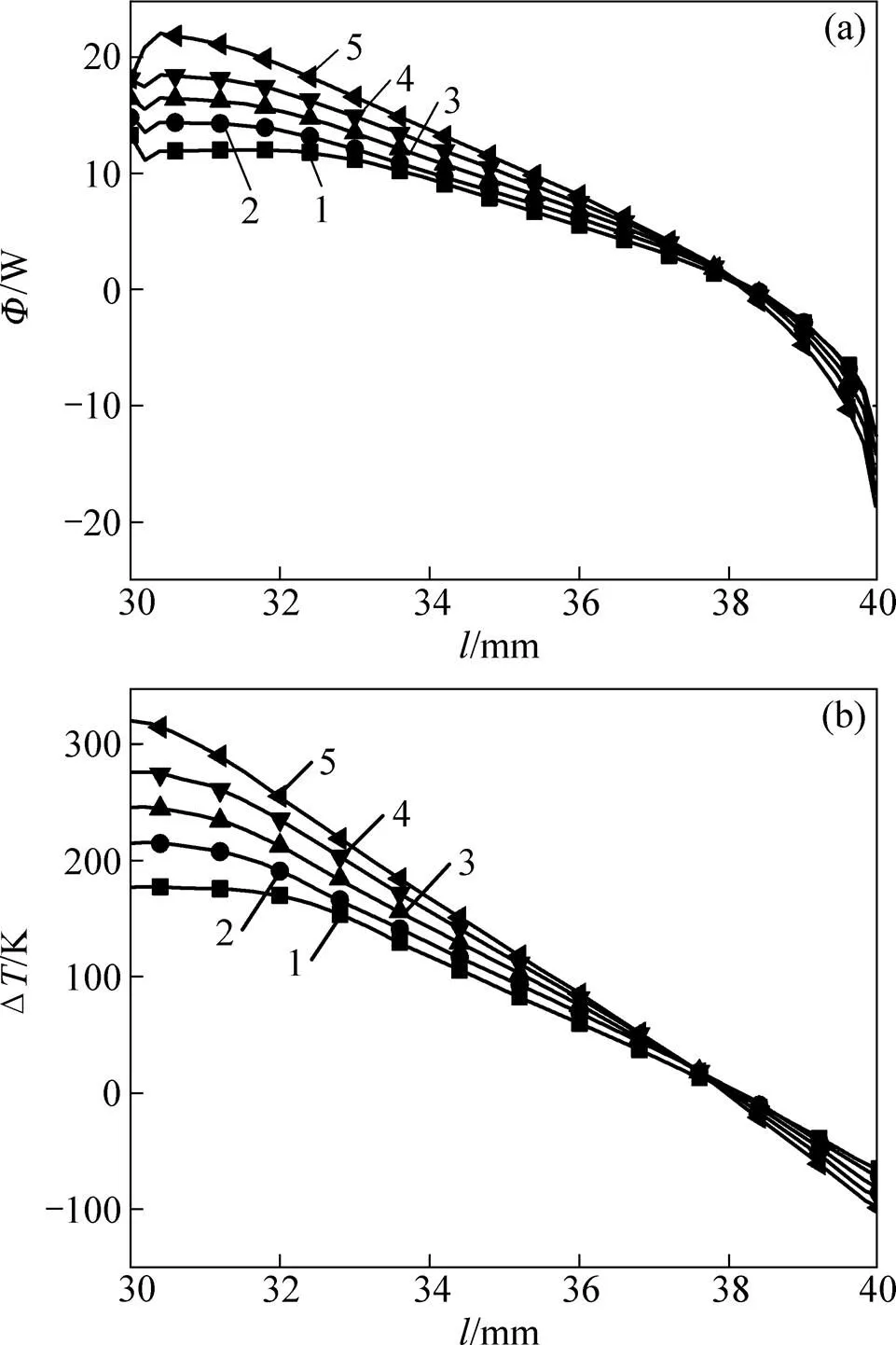
(a) 热流；(b) 温差

图11(a)所示为时刻2在不同热端温度下板叠表面热流量分布，图11(b)所示为板叠表面与流道中心温差(板叠表面温度减去流道中心处的温度)分布。从图11可见：与时刻1一样，随着热端温度升高，板叠热流量与温差都逐渐增大。但与时刻1不同的是：在时刻2时，热流量与温差的零点位置向左移动到接近板叠中间的位置即板叠表面，吸热与放热的面积接近，且吸收与放出的热量基本相同，所以，板叠的总热流量接近于0 W。

(a) 热流；(b) 温差

图12(a)所示为时刻3时不同热端温度下板叠表面热流量分布，图12(b)所示为板叠表面与流道中心温差(板叠表面温度减去流道中心处的温度)分布。从图12可见：与时刻1时刻2的变化规律一样的是，随着温度的升高，热流量及温差都逐渐增大，而与时刻1相反，此时板叠大部分位置(0.032~0.040 m)的温度都比气体温度低，所以，板叠大部分位置都从气体中吸热，只有板叠的前面一小段是板叠向气体放热，这也正是此时板叠总体呈现出从气体中吸热的原因。而这是因为此时流体以较大的速度向正向流动，使得高温流体向低温端流，导致大部分位置流体的温度都要高于板叠的温度。

(a) 热流；(b) 温差

结合这3种时刻的板叠表面热流及温差分布，板叠高温端的一小段温度总是比对应位置处的流体温度高，即该部分总是板叠向气体放热；而接近低温端的一小段，其温度总比对应位置处的流体温度低，所以，这部分则总是吸收气体中的热量。这也是热声效应的宏观表现，即气体工质不断地从高温端吸收热量，然后在低温端放出热量，并将部分热量转换成声功输出。此外，从时刻1到时刻3，板叠热流量的零点位置从板叠的右半段移动到板叠的左半段，这主要是受内部流体流向的影响。时刻1的流体朝负向即从低温端流向高温端，这使得大量的低温流体向高温端流动，从而使得大部分位置的板叠温度比流体温度高。时刻2的流体朝正向流动，即在时刻1至时刻2这段时间内，流体流向发生了逆转，因此，使得从低温端流过来的流体越来越少，而从高温端流向低温端的高温流体增多，这相当于缩小了板叠与流体的温差；随着流体正向流速的不断增大，又使得大量的高温流体流动到低温端，从而使得板叠大部分位置的温度都低于流体温度。

3 结论

1) 热端温度会增大系统的波动压力与体积流率的振幅，同时也会对两者的相位差产生影响。随着热端温度的增大，相位差呈下降趋势。

2) 系统声功率并不随热端温度的升高呈线性变化，即并非热端温度越高越好，对于某一具体结构的热声发动机，存在1个最佳热端温度使其声功输出 最大。

3) 随着热端温度升高，板叠与气体工质间换热量不断增大，且板叠向气体放出的热量总比从气体中吸收的多，而多出的这部分热量为声功的主要能量来源。

4) 靠近高温端的一小段板叠始终向气体放热，靠近低温端的一小段板叠则始终从气体中吸收热量，即这2部分板叠相当于实际系统中的高低温端换热器。

[1] Backhaus S, Swift G W. A thermoacoustic Stirling heat engine[J]. Nature, 1999, 399(6734): 335−338.

[2] 蒋彦龙, 陈国邦, Thummes G, 等. 20 K 以下温区单级脉管制冷机直流控制实验研究[J]. 低温工程, 2002(6): 11−15. JIANG Yanlong, CHEN Guobang, Thummes G, et al. The DC control experimental study of single-stage pulse tube cryocooler during temperature range of below 20 K[J]. Cryogenic Engineering, 2002(6): 11−15.

[3] 蒋宁, 陈国邦, Lindemann U, 等. 1.27 K3He 二级脉管制冷机性能研究[J]. 低温工程, 2004(5): 1−7. JIANG Ning, CHEN Guobang, Lindemann U, et al. The study of 1.27 K3He secondary vascular chiller performance[J]. Cryogenic Engineering, 2004(5): 1−7.

[4] 吴张华, 满满, 罗二仓, 等. 500 W 行波热声发电样机的实验研究[J]. 科学通报, 2011, 56(14): 1088−1090. WU Zhanghua, MAN Man, LUO Ercang, et al. The experimental study of 500 W travelling wave thermoacoustic prototype[J]. Chinese Science Bulletin, 2011, 56(14): 1088−1090.

[5] 余国瑶, 罗二仓, 戴巍, 等. 热声发动机的CFD数值模拟[J]. 工程热物理学报, 2010, 31(1): 6−10. YU Guoyao, LUO Ercang, DAI Wei, et al. CFD Numerical simulation of thermoacoustic heat engines[J]. Journal of Engineering Thermophysics, 2010, 31(1): 6−10.

[6] Cheng C F, David Ngu T W. CFD study of traveling wave with in a piston-less striling heat engine[J]. Computa-tional Fluid Dynamics, 2009, 41(2): 813−814.

[7] GUO Zengyuan, WANG Song. Novel concept and approaches of heat transfer enhancement[C]//Proceedings of Symposium on Energy Engineering in the 21st Century 2000. Hongkong, China: SEE, 2000: 118−126.

[8] GUO Zengyuan, LI Deyu, WANG Buxuan. A novel concept for convective heat transfer enhancement[J]. International Journal of Heat and Mass Transfer, 1998, 41(14): 2221−2225.

[9] Benavides E M. An analytical model of self-starting thermoacoustic engines[J]. Journal of Applied Physics, 2006, 99(11): 114905-1−114905-7.

[10] 林建忠, 阮晓东, 陈邦国, 等. 流体力学[M]. 北京: 清华大学出版社, 2005: 9−59. LIN Jianzhong, RUAN Xiaodong, CHEN Bangguo, et al. Fluid mechanics[M]. Beijing: Tsinghua University Press, 2005: 9−59.

[11] 杜功焕, 朱哲民, 龚秀芬, 等. 声学基础[M]. 南京: 南京大学出版社, 2001: 182−200. DU Gonghuan, ZHU Zhemin, GONG Xiufen, et al. The acoustics foundation[M]. Nanjing: Nanjing University Press, 2001: 182−200.

[12] 刘伟, 刘志春, 黄素逸. 湍流换热的场物理量协同与传热强化分析[J]. 科学通报, 2010, 55(3): 281−288. LIU Wei, LIU Zhichun, HUANG Suyi. Turbulent heat transfer quantity coordination and strengthening heat transfer analysis[J]. Chinese Science Bulletin, 2010, 55(3): 281−288.

[13] Zink F, Vipperman J, Schaefer L. CFD simulation of thermoacoustic cooling[J]. International Journal of Heat and Mass Transfer, 2010, 53(19): 3940−3946.

[14] 刘益才, 张明研, 黄谦, 等. 热声热机板叠式回热器结构数值计算[J]. 中南大学学报(自然科学版), 2010, 41(3): 1186−1189. LIU Yicai, ZHANG Mingyan, HUANG Qian, et al. The numerical calculation of thermoacoustic engine in stack regenerator structure[J]. Journal of Central South University (Natural and Technology), 2010, 41(3): 1186−1189.

[15] 贾正中. 驻波型热声发动机性能的理论与实验研究[D]. 杭州: 浙江大学机械与能源工程学院, 2006: 34−48. JIA Zhengzhong. Standing wave type thermoacoustic engine performance of theoretical and experimental research[D]. Hangzhou: Zhejiang University. College of Mechanical and Energy Engineering, 2006: 34−48.

[16] 张春萍. 热声核特性参数实验研究及高频微型热声实验装置的研制[D]. 武汉: 华中科技大学能源与动力工程学院, 2011: 45−91. ZHANG Chunping. Thermoacoustic characteristic parameters of experimental research and development of high frequency miniature thermoacoustic experiment device[D]. Wuhan: Huazhong University of Science and Technology. College of Energy and Power Engineering, 2011: 45−91.

Numerical research on effect of hot end temperature on thermoacoustic engine performance

ZHANG Kai, LIU Yicai, XIE Haibo, WANG Shouchuan, LIU Yaqiang, WU Tong

(School of Energy Science and Engineering, Central South University, Changsha 410083, China)

The synergy model was established and the computational fluid dynamics (CFD) method was used to conduct the two-dimensional numerical simulation on the 1/4 wavelength standing wave thermoacoustic engine. The changes of sound power within the system under different hot end temperatures and convective heat transfer characteristics between the stacks and the working gas were analyzed. The results show that fluctuations of pressure and amplitude of volume flow rate increase with the increase of the hot side temperature, that phase has a downward trend with the increase of the hot end temperature, and that the thermoacoustic engine with specific structure corresponds to the optimum temperature of the hot end allowing acoustic power output of the system to reach the maximum. Heat transfer between stacks and the working gas also increases with the increase of the hot end temperature, and sound power is not proportional to the size of the heat flow. There is a fixed endothermic and exothermic region in the stacks.

thermoacoustic engine; phase difference; numerical simulation; field synergy

10.11817/j.issn.1672-7207.2015.10.050

TB65

A

1672−7207(2015)10−3936−08

2014−11−10；

2015−01−20

国家自然科学基金资助项目(51276201)(Project (51276201) supported by the National Natural Science Foundation of China)

刘益才，教授，从事热声热机、斯特林制冷机、高效蓄冷蓄热材料、微型低温制冷机以及微型制冷系统振动和噪声抑制等研究；E-mail：lyccsu@csu.edu.cn

(编辑 陈灿华)