约简概念格与模糊优选在地下工程岩体质量评判中的应用
2015-10-14邬书良陈建宏周智勇杨珊
邬书良,陈建宏,周智勇,杨珊
约简概念格与模糊优选在地下工程岩体质量评判中的应用
邬书良,陈建宏,周智勇,杨珊
(中南大学资源与安全工程学院,湖南长沙,410083)
为了对地下工程岩体质量进行正确评判并提高评判效率,利用约简概念格对影响地下工程岩体稳定性的5项指标进行约简。5项指标分别为岩石质量指标、岩石单轴饱和抗压强度、完整性系数、结构面强度系数和地下水渗水量。以广州抽水蓄能电站1期地下工程岩体17 组实测数据和8 组插值数据作为学习样本,利用约简概念格对指标约简后得到岩石质量指标、岩石单轴饱和抗压强度和结构面强度系数这3项指标,用模糊优选法对约简后样本进行岩体质量评判,评判结果与实测结果吻合,然后将该模型用于该电站2 期地下工程岩体质量评价。研究结果表明:利用约简概念格与模糊优选构建的模型的评判结果和粗糙集−逼近理想解的排序法(RS-TOPSIS)、突变级数法、人工神经网络(ANN)和支持向量机(SVM)的评判结果一致。利用约简概念格与模糊优选构建的模型减少了评判所需的指标,提高了评判效率。
地下工程;岩体质量评判;属性约简;约简概念格;模糊优选法
地下工程岩体质量评判是一项涉及多种影响因素的复杂系统工程[1−3],正确的岩体质量评判是进行工程设计、灾害控制的重要依据。目前国内外对工程岩体质量评判方法较多[4−9],除了传统岩石工程中的岩石质量指标法(RQD)、岩体地质力学分类法(RMR)、巴顿岩体质量分类法(Q法),近年来有许多新的理论也用于岩体质量评判[10−16],如胡建华等[4]利用粗糙集对影响地下工程岩体质量各因素进行分析并得到权重,同时对岩体质量进行分类;宫凤强等[16]将突变级数法应用于地下工程围岩稳定性分类;其他的评判方法还有未确知测度理论法[7]、可拓学[1, 5, 8]等。这些方法对工程岩体质量分类虽然取得了一定效果,但它们都是在所能得到的影响因素上直接对岩体质量进行评判,而没有考虑在对岩体质量评判时,这些因素是否都是必要因素。因此,岩体质量评判效率较低。概念格是进行知识表示和数据分析的一种有效工具,它已成功应用于许多工程方面的数据处理和信息挖掘[17−19]。本文作者利用概念格作为约简工具,将已知的影响因素进行约简,利用约简后的指标通过模糊优选法建立计算模型对地下工程岩体质量进行综合评价,得到岩体质量的分级结果,并将该模型应用于实际工程,验证该评判模型的可行性和有效性。
1 约简概念格
1.1 概念格的基本思想
概念格又称为形式概念分析,它以其优异的性质成功应用于知识发现等诸多领域。概念格的每个节点即是一个形式概念,它由外延(或对象)和内涵(或属性)这2部分组成。
一个形式背景=(,,)由对象集合、属性集合和二者之间的关系组成。对于一个形式背景的对象集∈(),属性集∈()定义以下映射和:

那么从形式背景中得到的每一个满足以上2个映射的二元组(,)为一个概念,称为概念(,)的外延,为概念(,)的内涵。
对于概念(1,1)和(2,2),若满足或,则称(1,1)为子概念或亚概念,(2,2)为父概念或超概念。由形式背景中所有超概念−亚概念的偏序关系所诱导出的格即为概念格[20]。
1.2 基于概念格的属性约简
基于概念格的属性约简的基本思想是通过构建一个完整的概念格,求出其中的相融可辨概念极其亏属性,从条件属性的幂集中剔除包含亏属性的集合,最终得到可约简的属性集。
若2个对象概念(1,1),(2,2)共有1个父概念(,) ,且该父概念(,)的内涵中不包含决策属性,但∨,则称该公共父概念(,)为概念(1,1),(2,2)的相融可辨概念。其中:V为决策属性集。
对于概念(,) ,若原决策表中的条件属性C满足,则满足此条件的所有条件属性C的集合称为概念(,) 相对于初始决策表的亏属性[21]。
2 模糊优选法
模糊优选的基本思想[22]是确定方案集关于目标集隶属于模糊概念“优”的隶属度,即优属度,再根据模糊优选公式得到待评价方案关于优的相对隶属度,从而得到方案的优劣顺序。
设系统有个待选优的对象集和个指标的目标集,则方案的指标特征矩阵为
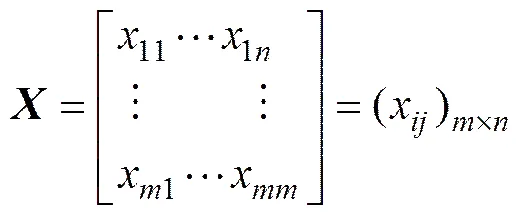
=1,2,…,,=1,2,…,(2)
其中:x为对象目标的特征值。由于目标间的量纲通常差异较大,所以需将指标特征值矩阵转化为规范化矩阵=(r)m×n。
对于效益型,即越大方案越好;对于成本型,即越小方案越好。
式中:r为对象目标对优的隶属度。将矩阵变为对应的隶属度矩阵,称为相对优属度矩阵,
,
=1,2,…,,=1,2,…,(4)
在相对优属度矩阵中,可以确定最优相对优属度=(1,2,…,g)T=(1,1,…,1)T,称为系统的优等对象;最劣相对优属度=(1,2,…,b)T=(0,0,…,0)T,称为系统的劣等对象。
多目标决策中的指标间重要程度有差异,设指标权重向量为
=(1,2,…,w)T,0<w<1,(5)
优属度u的计算公式为
其中:为距离参数,一般取欧氏距离=2。
在计算出各对象的优属度u后,通过比较待评价对象的优属度,即可对待评价对象进行评判。
3 地下工程岩体质量评判模型的建立
3.1 评判指标的选取
参考有关地下工程岩体质量评价体系[1, 4−5, 16]及获取实际数据难易程度,并且从与岩石质量有关的岩性、岩体结构及地质构造等影响因素出发,选取岩石质量指标(QD)、岩石单轴饱和抗压强度(W)、岩体完整性系数(v)、结构面强度系数(f)和地下水渗水量()这5个指标作为影响地下工程岩体质量因素。
对照文献[4]中的规范及国家标准,根据5项指标,将岩体质量分为5个等级,如表1所示。

表1 地下工程岩体等级分类标准
3.2 地下工程岩体质量评判对象
以广州抽水蓄能电站的地下工程岩体作为评判对象。该电站分2期建成,分别设1条引水隧洞,采用独立地下厂房和开关站。以25组数据为训练样本,建立约简概念格与模糊优选的地下工程岩体质量评判模型,其中1~17组为电站一期实测数据[16]。由于实测岩体类别数据中Ⅰ,Ⅳ和Ⅴ级的岩体数据较少,为保证样本数据的均匀性与代表性,采用插值法[3]构建18~25组数据,使得样本的岩体类别完整。表2所示为地下工程岩体学习样本数据。
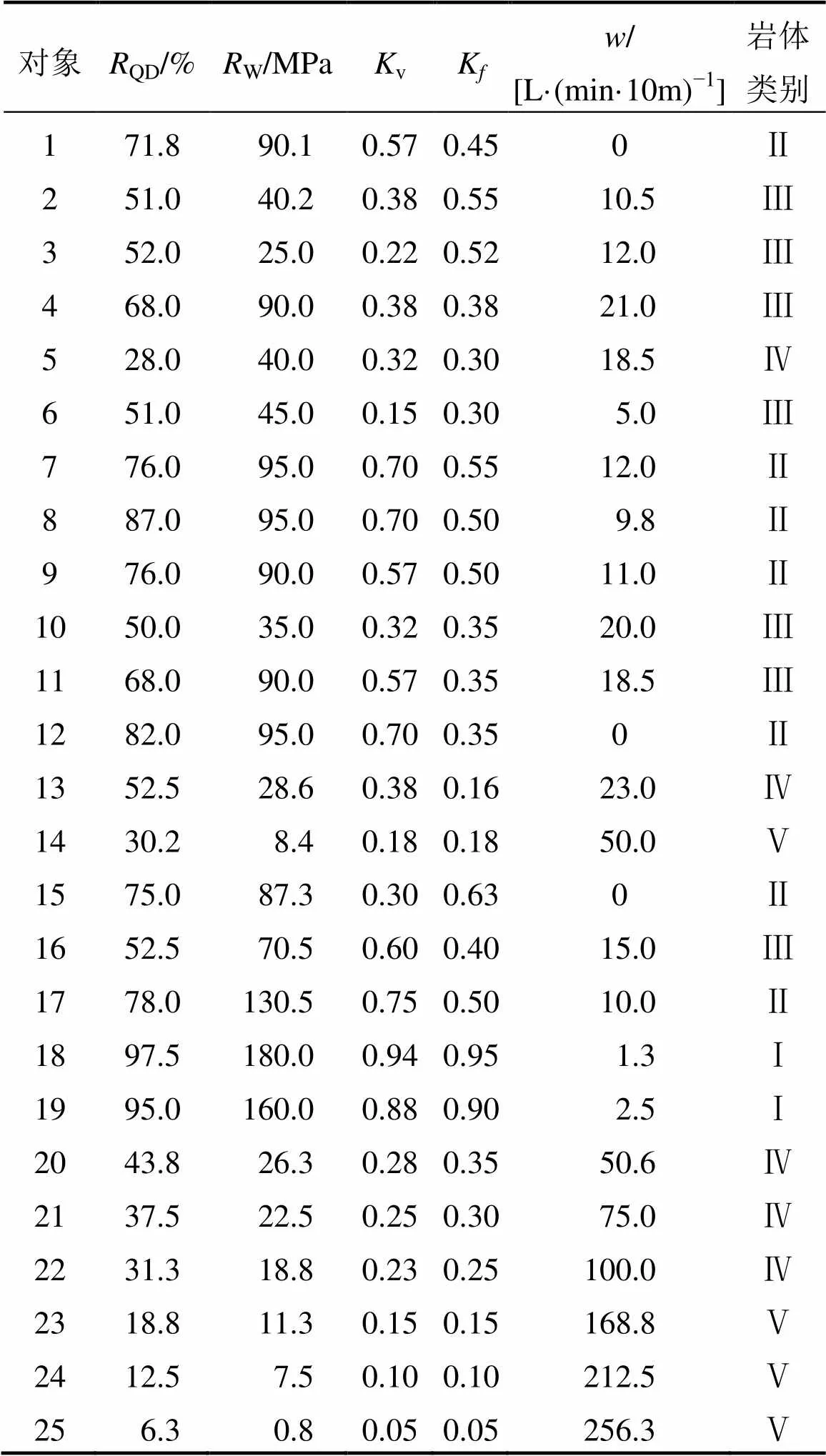
表2 地下工程岩体学习样本数据
从表2可以看出:由于5项判别指标不同,这些样本对应的岩体质量类别也不同。为了提高判别效率,考虑使用尽可能少的指标对岩体质量作出判别,需对所选取的5项评判指标进行约简。
3.3 评判指标的约简
约简概念格进行约简前,需要先将表2中的数据进行离散处理,形成一个评判决策表。参照表1中的指标分级标准,根据各自所属的Ⅰ~Ⅴ类别范围将表2中的指标数据进行离散化形成评判决策表如表3所示。由于决策表是对表2中的数据所处类别的表述,表3中仅列出部分决策表数据。
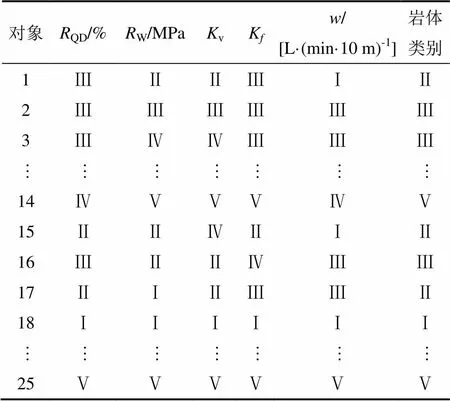
表3 评判决策表
从表3可以看出:5项评判指标和岩体类别都包含了Ⅰ~Ⅴ类,指标级别不同对应岩体类别也不同,除了采用插值法的第18~25组的指标类别与岩体类别相同以外,其他各组的指标类别与岩体类别差异都 很大。
概念格在对决策表进行知识发现时,它所需的是一种单值形式的数据表现形式,即形式背景。通过离散化处理得到的决策表,需要再将决策表转化为单值的形式背景。形式背景是一种数据信息表,根据决策表中各指标所包含的等级,分别划分为更细致的决策表。从表3可以看出:5项评判指标及岩体类别都包含了Ⅰ~Ⅴ 5种类别,所以形式背景就会有30列,即条件属性及决策属性一共有30项。然后每个待评价对象在其所具有的条件属性及岩石类别下做标记,最后得到概念格计算所需的形式背景。,,,和分别为岩石质量指标QD、岩石单轴饱和抗压强度W、岩体完整性系数v、结构面强度系数K和地下水渗水量这5个指标;为岩石类别。下标数字1,2,3,4和5分别为等级Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ,如1~5分别为岩石质量指标QD的Ⅰ~Ⅴ这5个等级。
利用约简概念格理论对形式背景进行属性约简,找出其中的相融可辨概念,并将这些相融可辨概念对应的属性提取出来,包括:{},{4},{3},{2},{1},{4},{2},{3},{1},{5},{4},{2},{5},{4},{3},{3,3},{2,3},{2,3},{3,2},{4,4},{3,4},{3,3},{2,4},{4,4},{4,3},{3,3},{3,3},{2,2},{3,3,3},{2,2,3},{3,2,2},{3,3,3},{2,2,4},{3,4,3},{3,4,3},{3,3,4,3}。
则不可同时约简的亏属性为{,,,,,,,,,,,,,,,,,,,,}。
当某个属性是不可约简的,那么它的超集也必定不可约简,所以,不可约简的属性的最简形式为{,,,,}。
最后,从5项评判指标的幂集中将包含属性{,,,,}的集合剔除,得到属性集{,,,},那么对应的约简为{,,,},即约简后一共可以得到4个属性集,分别为{岩石质量指标QD,岩石单轴饱和抗压强度W,岩体完整性系数v,地下水渗水量},{岩石质量指标QD,结构面强度系数f,地下水渗水量},{岩石质量指标QD,岩体完整性系数v,结构面强度系数f}和{岩石质量指标QD,岩石单轴饱和抗压强度W,结构面强度系数f}。
对比这4组约简,第1组约简后有4项指标,后3组只有3项指标,显然后3组比第1组更为精简。对比后面3组,从表2可见:有部分指标数据恰好处于工程岩体等级分类标准的分界值上,这些值势必会影响评判的结果,所以需要对比这3组约简所包含的分界值的个数。通过对表2中岩体学习样本数据的观察,这3组约简所包含的分界值分别为5,5和3个,所以最后选择包含的分界值最少的约简{岩石质量指标QD,岩石单轴饱和抗压强度W,结构面强度系 数f}。
3.4 约简概念格与模糊优选的评判模型
根据指标约简结果,将表2中的岩石质量指标QD、岩石单轴饱和抗压强度W、结构面强度系数K及实测等级数据提取出来,同时把表1中的岩体等级分类标准相应指标数据也作为待评价对象。由于各指标间量纲的差异,将选取的数据进行规范化处理,约简后的3项指标QD,W和f均为越大越优,则使用式(3)对指标属性进行规范化处理,规范化后的学习样本结果如表4所示。由于结果较多,表4中仅列出部分规范化后的学习样本结果。

表4 约简后的学习样本
在多目标决策优选中,由于各指标对结果的影响程度不同,需确定各指标的权重。将表4中的指标数据及实测数据进行训练,利用遗传算法,得到QD,W和f的权重分别为0.410,0.365和0.225。
根据式(6)对规范化后的样本数据进行计算,得到各对象的优属度,其优属度如表4所示。从表4可以看出,地下工程岩体质量的优属度分类为:
Ⅰ级岩体:0.896 4≤u≤1.000 0
Ⅱ级岩体:0.598 0≤u<0.896 4
Ⅲ级岩体:0.253 4≤u<0.598 0
Ⅳ级岩体:0.052 2≤u<0.253 4
Ⅴ级岩体:0≤u<0.052 2
将各对象的优属度对照岩体质量分类的优属度范围,得到相应的岩石质量评判。从表4可知:除了第14组将Ⅴ级岩体判为Ⅳ级岩体以外,其他评判结果与实际相符。这与文献[16]误判结果一致,其原因可能是该组岩体质量介于两级之间,使得把介于两级之间的岩体判为其中的一级。
4 工程应用
为了检验约简概念格与模糊优选的岩体质量评价模型的高效性与准确性,利用模型对广州抽水蓄能电站2期工程的8组岩体进行质量评价,评价指标为约简后的QD,W和f这3项,并与利用5项指标RS-TOPSIS法[4]、突变级数法[16]、人工神经网络(ANN)[14]和支持向量机(SVM)[15]所得的评判结果进行比较,其结果如表5所示。
从表5可以看出:利用约简概念格和模糊优选模型所得的评判结果与RS-TOPSIS法、突变级数法、ANN法、SVM法的评判结果相同,表明了约简概念格和模糊优选模型应用于岩体质量评价的有效性;同时,由于该模型只需要用3项指标就可以对岩体质量进行正确的评判,与RS-TOPSIS法、突变级数法、ANN法、SVM法利用5项指标进行评判相比,所需的评判指标数少,表明了该模型对岩体质量进行评判更为高效。

表5 第2期工程约简概念格与模糊优选的岩体质量评判结果
5 结论
1) 以25组岩体质量数据为学习样本,通过约简概念格对其进行知识发现,最后将5项指标减少到3项指标,表明了约简概念格对地下工程岩体质量指标约简时的有效性。
2) 利用约简概念格与模糊优选构建地下工程岩体质量评判模型。将所构建的模型对25组学习样本进行评判,除1组数据误判外,其他24组评判结果与实测结果相同,表明了该模型对地下工程岩体质量评判可靠。
3) 将该模型应用于2期工程的部分岩体质量进行评判,评判结果与RS-TOPSIS法、突变级数法、ANN法和SVM法所得的评判结果一致,表明利用约简概念格与模糊优选构建地下工程岩体质量评判模型科学有效,并且减少了评判时所需的指标,提高了评判效率。
[1] 刘爱华, 程力, 董陇军. 可拓学理论在东戈壁露天矿工程岩体质量评价中的应用[J]. 中南大学学报(自然科学版), 2013, 44(7): 2841−2847. LIU Aihua, CHENG Li, DONG Longjun. Evaluation of engineering rock mass quality based on theory of extenics in Dong Gebi openpit mine[J]. Journal of Central South University (Science and Technology), 2013, 44(7): 2841−2847.
[2] 王明华, 白云, 张电吉. 含软弱夹层岩体质量评价研究[J]. 岩土力学, 2007, 28(1): 185−187. WANG Minghua, BAI Yun, ZHANG Dianji. A study on rock mass structure feature and surrounding rock ranking for Xiluodu Hydropower Station[J]. Rock and Soil Mechanics, 2007, 28(1): 185−187.
[3] 杨朝晖, 刘浩吾. 地下工程围岩稳定性分类的人工神经网络模型[J]. 四川联合大学学报(工程科学版), 1999, 3(4): 66−72. YANG Zhaohui, LIU Haowu. Artificial neural network model for the stability classification of adjoining rock of underground construction[J]. Journal of Sichuan Union University (Engineering Science Edition), 1999, 3(4): 66−72.
[4] 胡建华, 尚俊龙, 雷涛. 基于RS-TOPSIS法的地下工程岩体质量评价[J]. 中南大学学报(自然科学版), 2012, 43(11): 4412−4419. HU Jianhua, SHANG Junlong, LEI Tao. Rock mass quality evaluation of underground engineering based on RS-TOPSIS method[J]. Journal of Central South University (Science and Technology), 2012, 43(11): 4412−4419.
[5] 康志强, 冯夏庭, 周辉. 基于层次分析法的可拓学理论在地下洞室岩体质量评价中的应用[J]. 岩石力学与工程学报, 2006, 25(S2): 3687−3693. KANG Zhiqiang, FENG Xiating, ZHOU Hui. Application of extenics theory to evaluation of underground cavern rock quality based on stratification analysis method[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(S2): 3687−3693.
[6] 陈鹏宇, 余宏明, 谢凯, 等. 基于支持度的隧道围岩质量分级组合评价方法[J]. 岩土工程学报, 2013, 35(12): 2233−2237. CHEN Pengyu, YU Hongming, XIE Kai, et al. Combination evaluation method for classification of surrounding rock quality of tunnels based on support degree[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(12): 2233−2237.
[7] 唐海, 万文, 刘金海. 基于未确知测度理论的地下洞室岩体质量评价[J]. 岩土力学, 2011, 34(4): 1181−1185. TANG Hai, WAN Wen, LIU Jinhai. Evaluation of underground cavern rock quality based on uncertainty measure theory[J]. Rock and Soil Mechanics, 2011, 34(4): 1181−1185.
[8] 梁桂兰, 徐卫亚, 谈小龙. 基于熵权的可拓理论在岩体质量评价中的应用[J]. 岩土力学, 2010, 31(2): 535−540. LIANG Guilan, XU Weiya, TAN Xiaolong. Application of extension theory based on entropy weight to rock quality evaluation[J]. Rock and Soil Mechanics, 2010, 31(2): 535−540.
[9] 刘爱华, 苏龙, 朱旭波, 等. 基于距离判别分析与模糊数学的岩体质量评判法[J]. 采矿与安全工程学报, 2011, 28(3): 462−467. LIU Aihua, SU Long, ZHU Xubo, et al. Rock quality evaluation based on distance discriminant analysis and fuzzy mathematic method[J]. Journal of Mining & Safety Engineering, 2011, 28(3): 462−467.
[10] 谢本贤, 陈沅江, 史秀志. 深部岩体工程围岩质量评价的IRMR法研究[J]. 中南大学学报(自然科学版), 2007, 38(5): 987−992. XIE Benxian, CHEN Yuanjiang, SHI Xiuzhi. IRMR method for evaluation of surrounding rock quality in deep rock mass engineering[J]. Journal of Central South University (Science and Technology), 2007, 38(5): 987−992.
[11] 常利营, 卢建移, 段波, 等. 基于Hopfield网络的地下工程围岩稳定性分类[J]. 岩土工程学报, 2011, 33(S1): 194−197. CHANG Liying, LU Jianyi, DUAN Bo, et al. Stability classification of adjoining rock of underground engineering based on Hopfield network[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(S1): 194−197.
[12] Sapigni M, Berti M, Bethaz E, et al. TBM performance estimation using rock mass classifications[J]. Internal Journal of Rock Mechanics and Mining Sciences, 2002, 39(2): 771−788.
[13] Arild P, Eina B. Use and misuse of rock mass classification systems with particular reference to the Q-system[J]. Tunneling and Underground Space Technology, 2006, 21(6): 575−593.
[14] 蔡广奎. 围岩稳定性分类的BP网络模型的研究[D]. 南京: 河海大学土木工程学院,2001: 49−54. CAI Guangkui. Study of the BP neural network on the stability classification of surrounding rocks[D]. Nanjing: Hohai University. School of Civil Engineering, 2001: 49−54.
[15] 赖永标. 支持向量机在地下工程中的应用研究[D]. 青岛: 山东科技大学资源与环境工程学院, 2004: 51−75.LAI Yongbiao. Application and study of support vector machine in the underground engineering[D]. Qingdao: Shandong University of Science and Technology. College of Resource and Environment Engineering, 2004: 51−75.
[16] 宫凤强, 李夕兵, 高科. 地下工程围岩稳定性分类的突变级数法研究[J]. 中南大学学报(自然科学版), 2008, 39(5): 1081−1086. GONG Fengqiang, LI Xibing, GAO Ke. Catastrophe progression method for stability classification of underground engineering surrounding rock[J]. Journal of Central South University (Science and Technology), 2008, 39(5): 1081−1086.
[17] 王贤敏, 牛瑞卿. 三峡库区基于概念格算法的遥感岩性分析[J].遥感技术与应用, 2009, 24(1): 32−39. WANG Xianmin, NIU Ruiqing. Analysis of lithology with remote sensing image based on concept grid algorithm in three gorges[J]. Remote Sensing Technology and Application, 2009, 24(1): 32−39.
[18] 滕广青. 基于概念格的社区用户知识需求模型研究[J]. 情报科学, 2011(1): 108−112. TENG Guangqing. Research on demand model of knowledge about community users based on concept lattice[J]. Information Science, 2011(1): 108−112.
[19] 文莹, 肖明清, 盛晟, 等. 基于概念格的航空雷达故障诊断研究[J]. 计算机测量与控制, 2013, 21(10): 2612−2614. WEN Ying, XIAO Mingqing, SHENG Sheng, et al. study of fault diagnosis of airborne radar based on concept lattice[J]. Computer Measurement & Control, 2013, 21(10): 2612−2614.
[20] 李云. 概念格分布处理及其框架下的知识发现研究[D]. 上海: 上海大学计算机科学与工程学院, 2005: 7−17. LI Yun. Research on distributed treatment of concept lattices and knowledge discovery based on its framework[D]. Shanghai: Shanghai University. School of Computer Science and Engineering, 2005: 7−17.
[21] 杨凯, 马垣. 基于概念格的多层属性约简方法[J]. 模式识别与人工智能, 2012, 25(6): 922−927.YANG Kai, MA Yuan. Multi-Level attribute reduction methods based on concept lattice[J]. Pattern Recognition and Artificial Intelligence, 2012, 25(6): 922−927.
[22] 方国华, 黄显峰. 多目标决策理论、方法及其应用[M]. 北京: 科学出版社, 2011: 168−172. FANG Guohua, HUANG Xianfeng. Multi-objective decision theory and its application[M]. Beijing: Science Press, 2011: 168−172.
Application of reduced concept lattice and fuzzy optimum selection in rock mass quality evaluation of underground engineering
WU Shuliang, CHEN Jianhong, ZHOU Zhiyong, YANG Shan
(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)
In order to evaluate rock mass quality of underground engineering correctly and improve efficiency, reduced concept lattice was used to reduce factors which controlled the stability of underground rock. The five factors involved were rock quality designation, uniaxial compressive strengthen, integrality coefficient, strengthen coefficient of structural plane and seepage measurement of groundwater, respectively. 17 samples of the first stage underground project in Guangzhou pump accumulator electricity station and another 8 samples produced by the interpolation method were taken as the learning samples. Reduced concept lattice was used to reduce factors and 3 factors including rock quality designation, uniaxial compressive strengthen and strengthen coefficient of structural plane were retained. Then fuzzy optimum selection was used to evaluate rock mass quality of the reduced samples, and evaluation results were consistent with measured results. Then the model was applied to predict the evaluation of the second stage project. The results show that the evaluation results using reduced concept lattice and fuzzy optimum selection agree well with those of RS-TOPSIS method, the catastrophe progression method, artificial neural network(ANN) method, and support vector machine (SVM) method. The reduced concept lattice and fuzzy optimum selection model reduces the required control factors and improves the efficiency of the evaluation.
underground engineering; rock quality evaluation; attribute reduction; reduced concept lattice; fuzzy optimum selection
10.11817/j.issn.1672-7207.2015.10.042
TU457
A
1672−7207(2015)10−3872−07
2014−12−13;
2015−02−20
国家自然科学基金资助项目(51374242);中央高校基本科研业务费专项资金资助项目(2014zzts056)(Project (51374242) supported by the National Natural Science Foundation of China; Project (2014zzts056) supported by the Foundamental Research Funds for the Central Universities)
陈建宏,博士,教授,博士生导师,从事金属矿开采方面的研究;E-mail:cjh@263.net
(编辑 罗金花)
