求张量扩展特征值的幂法

王佳佳,胡毅庆,赵金玲,徐 尔



求张量扩展特征值的幂法

*王佳佳,胡毅庆,赵金玲,徐 尔

（北京科技大学数理学院，北京 100083）

针对与牛顿迭代相关的张量扩展特征值问题,在对已有张量特征值和幂法的研究基础上,提出了求解与牛顿迭代有关的张量扩展特征值和特征向量的幂法,分析了该幂法的收敛性。最后数值试验结果验证了该幂法的有效性。

牛顿法；张量；特征值；幂法；收敛性

0 引言

在多重线性数值代数中，高阶张量的特征值已经成为一项重要课题，并在多项式最优化、高阶马尔科夫链、超图理论等领域有广泛的应用。

文献[1]用幂法求解矩阵的特征值和特征向量，之后又对幂法进行改进，提出带位移幂法，对幂法进行了改进。文献[2]用幂法求阶实方阵的全部模（大于等于两个）最大的特征值及相应特征向量,进一步完善了幂法。目前一些学者对幂法和张量的深入研究，已经将矩阵幂法推广到求高阶张量的特征值，这使得对张量特征值的研究有了很大的进展。

文献[3]提出求解不可约非负张量最大特征值的幂法。文献[4]用高阶幂法解决高阶张量逼近问题，并证明了对称高阶幂法不一定收敛。文献[5]和文献[6]分别给出带位移对称高阶幂法和梯度算法计算实对称张量的Z-特征值，并证明其收敛性。李彤等人在文献[7]中研究了三阶对称张量特征值问题。

文献[8]指出了牛顿迭代与张量特征值之间有紧密的关系，提出了新的张量特征值问题：

本文在已有张量特征值与幂法的研究基础上，针对上述张量扩展特征值问题（1），给出求解其特征值的幂法，并证明了算法的收敛性，数值试验结果验证了该算法的有效性。

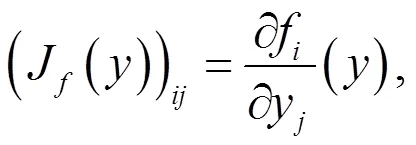
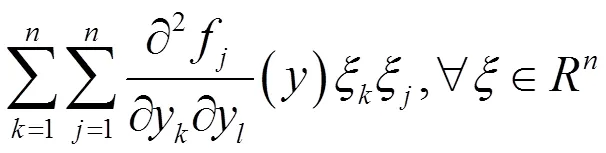
1 求张量扩展特征值的幂法

令

问题(1)变为

(4)

算法(幂法)

步骤1 令

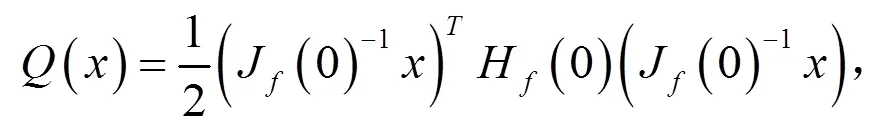
步骤2 计算

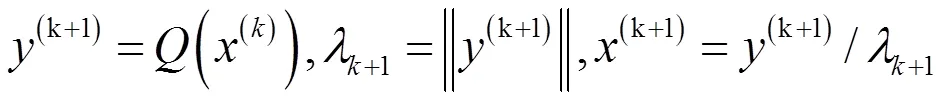
2 幂法的收敛性

记：

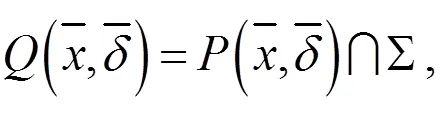
下面给出幂法的收敛性分析，需要下面的假设。

在假设下，问题(1)变为：

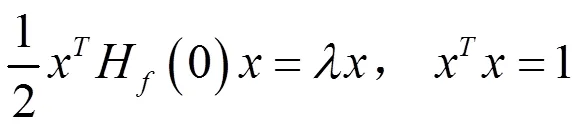
所以

(6)

得到

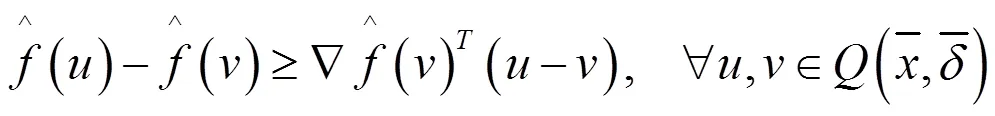
由引理的条件，得到

证明：(a) 由引理2得

3 数值试验

表1 幂法的实验结果

由表1知，幂法以概率1收敛到最大的正特征值，根据特征值定义算得另外两个特征值λ =1.264 9和λ =0.500 0，它们对应的特征向量分别为[0.632 5;±0.774 6;0.000 0]和[1.000 0;0.000 0;0.000 0]。另外，由于是三阶实对称张量，所以也是特征对，将算法改为和，其余不变，就可以求出负特征值。

表2 幂法的实验结果

表3 幂法的实验结果

通过上面三个数值算例，幂法以概率1收敛到最大特征值，表明给出的算法是有效的，故幂法可以有效地求出问题(1)的某些特征对。

4 总结

本文提出了计算与牛顿迭代相关的张量扩展特征值与特征向量的幂法，并证明了在假设条件下算法产生的序列收敛到特征对，不同的数值试验也表明了所提出算法的有效性。从数值结果来看，幂法可以有效求出张量的某些特征对，今后尚需进一步研究其它方法求解此类扩展特征值问题。

参考文献：

[1] 徐树方,高立,张平文.数值线性代数[M].2版.北京:北京大学出社,1999.

[2] 侯风波,汪永高.求阶实方阵的全部模最大的特征值及其相应特征向量的幂法[J].技术教育学报,1998, 9(3):16-19.

[3] Ng M,Qi L Q，Zhou G L. Finding the Largest Eigenvalue of a Nonnegative Tensor[J].SIAM Journal on Matrix Analysis and Applications,2009,31(3):1090-1099.

[4] Kofidis E, Regalia P A. On the best rank-1 approximation of higher-order supersymmetric tensors[J]. SIAM Journal on Matrix Analysis and Applications, 2002, 23(3): 863-884.

[5] Kolda T G, Mayo J R. Shifted power method for computing tensor eigenpairs[J]. SIAM Journal on Matrix Analysis and Applications, 2011, 32(4): 1095-1124.

[6] 梁浩,张向韵.对称张量Z-特征值的梯度算法及非负张量谱半径的一些性质[D].上海:华东师范大学,2014.

[7] 李彤,胡锡俊.关于三阶对称张量的特征值问题的研究[D]. 济南:山东大学,2013.

[8] Dupont T F, Ridgway Scott L. The power method for tensor eigenproblems and limiting directions of Newton iterates[J]. Numerical Linear Algebra with Applications, 2013, 20(6): 956-971.

[9] 薛山.MATLAB基础教程[M].北京:清华大学出版社,2011.

POWER METHOD FOR COMPUTING EXTENSION EIGENVALUES OF TENSOR

*WANG Jia-jia, HU Yi-qing, ZHAO Jin-ling, XU Er

(School of Mathematics and Physics, University of Science & Technology Beijing, Beijing 100083, China)

Tensor eigenvalue problem associated with the Newton iteration method was studied in this paper. Based on the research of tensor eigenvalues and power method, we firstly presented the power method that solved the extension eigenvalue and corresponding eigenvector of tensor. Furthermore, the convergence of the power method was proved. Finally, numerical results have shown that the method is effective.

Newton's method; tensor; eigenvalue; power method; convergence

1674-8085(2015)06-0012-05

O241.6

A

10.3969/j.issn.1674-8085.2015.06.003

2015-08-09；修改日期：2015-09-12

国家自然科学基金青年基金项目(11101028)；北京高校青年英才计划项目(YETP0385)

*王佳佳(1991-)，女，山西忻州人，硕士生，主要从事运筹与控制研究(E-mail:wjjustb2013@sina.com);

胡毅庆(1980-)，男，北京人，讲师，博士，主要从事运筹与控制研究(E-mail:hyq_math_ustb@foxmail.com);

赵金玲(1980-)，女，北京人，副教授，主要从事最优化计算方法研究(E-mail:jlzhao@ustb.edu.cn);

徐 尔(1961-)，女，北京人，副教授，硕士生导师，主要从事运筹学及其应用研究(E-mail:xuer_2009@sina.com).