Dini导数在函数凸性中的应用

布仁白乙拉，苏雅拉图



Dini导数在函数凸性中的应用

布仁白乙拉，*苏雅拉图

( 内蒙古师范大学数学科学学院, 内蒙古呼和浩特 010022)

本文建立了关于连续凸函数的含有Dini导数的一个不等式，并通过建立不等式给出了连续凸函数和连续严格凸函数的判据。

Dini导数；凸函数；单调增加；单调减少

1 预备知识

=

=

引理1.1[2]设函数区间的凸函数，那么对于的子区间和只要且就有。

引理1.2[3]设是区间上的凸函数，那么在的每个内点处，函数有有限的左导数和右导数它们都是单调增加的，并且。

引理1.3[3]设函数为上的连续函数，为点的四个Dini导数，若四者之一是单调增加的，则是凸的；若四者之一在上处处非负，那么在上非减。

引理1.4[4]设函数在上有定义，则是凸函数当且仅当对区间内满足条件的任意三点，有；而是严格凸函数当且仅当上述不等式中的小于号成立。

引理1.5[1]设函数在上连续，在（,）内均有限，则存在及使。

引理1.6[1]设为上的连续函数，且在（,）内有限，则是增（减）函数当且仅当

2 主要结果

为了证明主要结果，先给出一个非常有用的引理，其证明可用分析的常规方法，利用引理1.1和引理1.2给出。

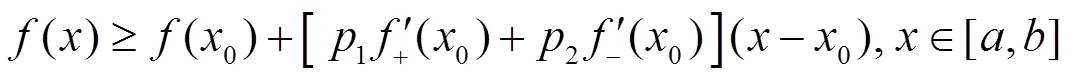
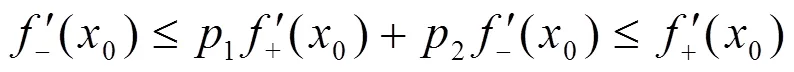
于是由引理2.1知，

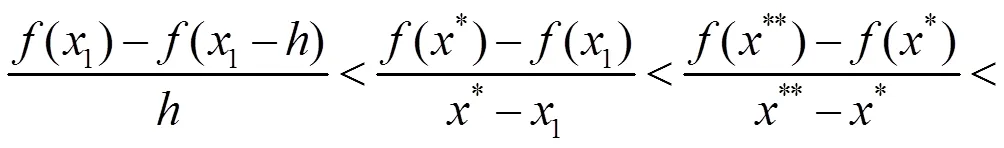
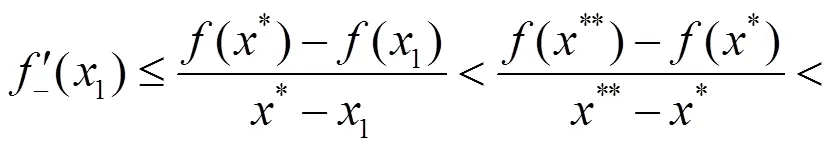
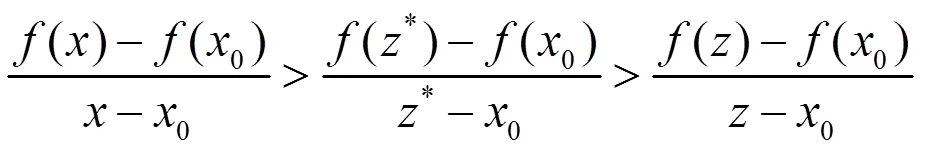
(2.3)

于是推导出

。

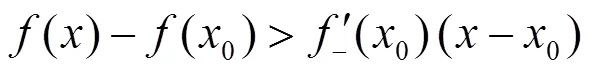
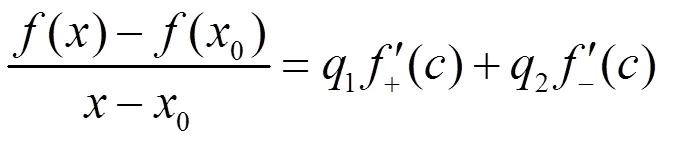
于是

即

这不等式显然等价于

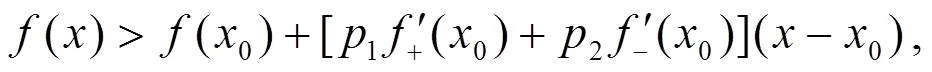
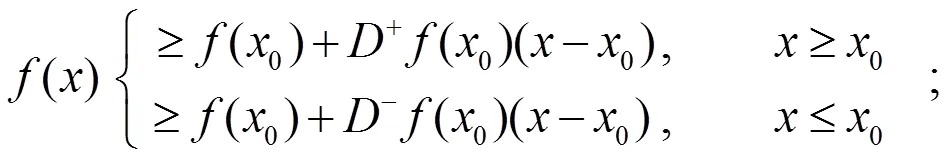
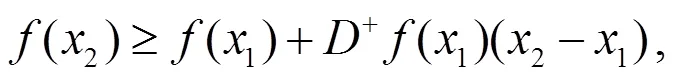
于是有

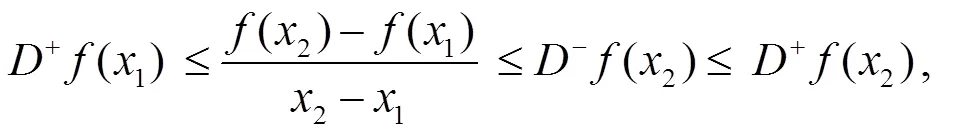
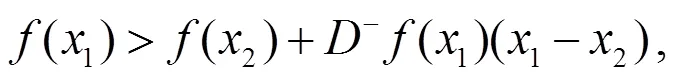
故有

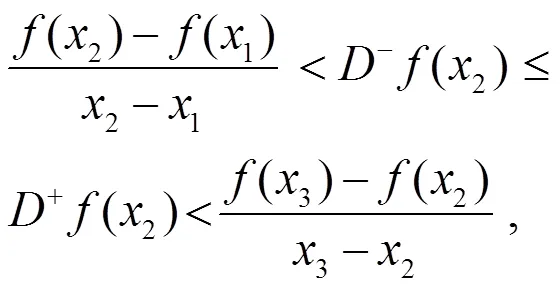
推论2.2[4]设是上的连续函数，在内可导，则是上的凸函数的充要条件为：对有

()是严格凸函数的充要条件为：对有。

推论2.3[4]设在上连续，在内二阶可微，则是上凸函数的充要条件为；是上严格凸函数的充要条件为且不在的任一子区间上恒为零。

参考文献：

[1] 闫革兴,战新山.关于含有Dini导数的函数中值定理[J].黑龙江大学学报,1992, 9 (3): 1-5.

[2] 王昆扬.实变函数论讲义[M].北京:高等教育出版社, 2011.

[3] Royden H L. Real Analysis[M].3版, 叶培新译, 北京:机械工业出版社,2006.

[4] 方企勒,沈燮昌. 数学分析[M].北京:高等教育出版社, 1986.

[5] 张国才,王恕达.带Dini导数的洛必达法则和达布定理[J].台州学院学报,2006,3(28): 15-16.

[6] 华东师范大学数学系.数学分析[M].3版. 北京:高等教育出版社, 2001.

THE APPLICATIONS OF DINI DERIVATIVE IN ONVEXITY OF FUNCTIONNS

Burenbaiyila,*Suyalatu

(College of Mathematics Science, Inner Mongolia N ormal University, hohhot 010022)

An inequality with Dini derivative about the continuous convex function is established. Some criteria for continuous convex function and continuous strictly convex function are given by establishing several inequalities with Dini derivative.

Dini derivative; convex function; strictly increasing; strictly decreasing

1674-8085(2015)06-0017-04

O171

A

10.3969/j.issn.1674-8085.2015.06.004

2015-05-16；修改日期：2015-08-19

内蒙古自然科学基金项目(2012MS1022)；内蒙古师范大学人才工程基金项目(RCPY-2-2012-K-034)

布仁白乙拉(1971-)，男，内蒙古科右中旗人，硕士生，主要从事Banach空间理论研究(E-mail:1121200709@qq.com);

*苏雅拉图(1960-)，男，内蒙古镶黄旗人，教授，硕士生导师，主要从事Banach空间理论研究(E-mail: suyila520@163.com)