W准对称非负定矩阵反问题的解
2015-10-13唐耀平周立平
唐耀平, 周立平
准对称非负定矩阵反问题的解
唐耀平, 周立平
(湖南科技学院数学与计算科学系, 湖南永州, 425100)
研究了准对称非负定矩阵反问题的解, 得到了这一问题有解的充分必要条件, 并在有解的情况下给出了解的一般表达式和算法例子。
准对称非负定矩阵; 反问题; 奇异值分解
近年来矩阵方程及其反问题的非负定解的研究己取得许多成果[1-2], 梁燕来[3]在张忠志等[4]定义的对称矩阵基础上定义了对称非负定矩阵, 并给出了对称非负定矩阵反问题解的一般表达式。根据他们的研究思想, 提出了准对称非负定矩阵的概念, 并研究了准对称非负定矩阵反问题的解。
首先给出准对称非负定矩阵的概念。

。 (2)

1 几个引理
引理1[5]。
引理2[6]设, 则当且仅当的主子式全部都大于0或等于0。
引理4[1]设,且有分解,则有, 使成立的充分必要条件是,且。并在有解时,解的表达式为

2 主要结果

,。 (6)
则式(3)有解的充分必要条件为

。 (8)
并且, 在有解的情况下, 解的一般表达式为
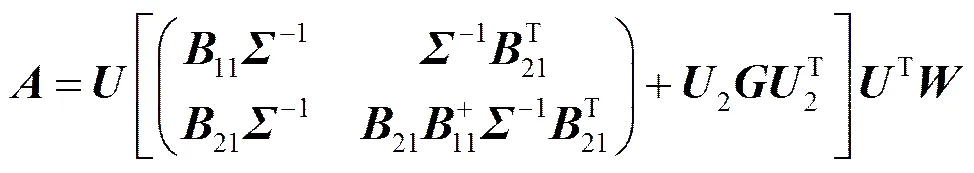
证明 设
,, (10)

。 (12)

。 (14)
且解的表达式为

由式(5)和(10)可得
。 (16)
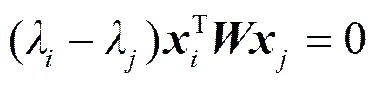
3 算法分析及数值计算
根据定理1, 可以给出式(3)解的算法和算例。
3.1 问题(3)的算法
3.2 问题(3)的算例
参考文献:
[1] 张磊. 对称非负定矩阵反问题解存在的条件[J]. 计算数学, 1989, 4: 337-334.
[2] 周树荃, 戴华. 代数特征值反问题[M]. 郑州: 河南科学技术出版社, 1991.
[3] 梁燕来, 张正杰, 周泽文.对称非负定矩阵反问题的解[J]. 华中师范大学学报: 自然科学版, 2004, 38(3): 280-283.
[4] 张忠志, 胡锡炎, 周富照.对称矩阵反问题的最小二乘解[J]. 湖南大学学报, 2001, 28(5): 6-10.
[5] 唐耀平.准对称矩阵反问题的最小二乘解[J].湖南科技学院学报, 2006, 27(11): 109-113.
[6] Johnson C R. Positive Definite Matrices [J]. Amer Math Montyly, 1970, 77: 259-264.
(责任编校:刘晓霞)
Solutions of inverse problems for-para-symmetric nonnegative definite matrices
Tang Yaoping, Zhou Liping
(Department of Mathematics and Computing Sciences, Hunan University of Science and Engineering, Yongzhou 425100, China)
The solutions of inverse problems for-para-symmetric nonnegative definite matrices are studies, and the necessary and sufficient conditions for the solvability of this problem are obtained. The expression and the example of general solution about this problem are given under case of having solution.
-para-symmetric nonnegative definite matrices; inverse problem for matrix; singular value decom- position
10.3969/j.issn.1672–6146.2015.02.011
O 241.6
1672–6146(2015)02–0032–03
唐耀平, 76122384@qq.com.
2014-10-09
湖南省自然科学基金项目(12JJ3077); 湖南省教育厅科研课题(13C335)。
