几类非线性回归模型的LS估计与非线性度量
2015-10-13肖兵
肖兵
几类非线性回归模型的LS估计与非线性度量
肖兵
(湖南文理学院数学与计算科学学院, 湖南常德, 415000)
研究了一类推广的非线性回归模型的最小二乘估计, 证明了其收敛性, 并推广到不满足高斯–马尔可夫条件的情形。研讨了几类特殊的部分非线性回归模型的参数估计及非线性程度度量, 探讨了参数最小二乘估计求法中迭代初值的选取, 提出了改进方向。
非线性度量; 可分离; 局部曲率; LS估计
众所周知,相当多的回归分析模型一般是线性模型, 其研究与应用已经比较完善, 但从严格意义上来看, 回归模型都具有不同程度非线性的情形(包括理论上的非线性参数和模拟研究中的非线性程度), 并带有很多约束条件。为了更好地解决实际问题, 研究带有约束条件等特殊情形的非线性回归模型是相当有意义的, 目前对非线性回归模型
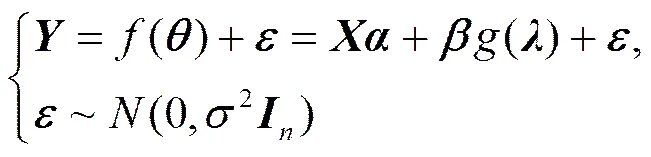
的研究有了较为完善的结果, 一般是对非线性项使用一阶近似进而使模型转化为线性模型得到了模型参数估计的基于迭代的近似解, 并以此研究其渐近性质。这里,为列满秩的× (-2)的设计矩阵,为-2维的未知参数向量,为统一命名的参数向量。为关于未知参数的非线性连续函数且解析式已知, 可能含有回归变量,是期望为0的维正态变量。
但上述研讨中都要求其随机扰动项满足高斯–马尔可夫条件假设并要求为满秩矩阵, 也很少考虑带约束条件。本文考虑这些条件不完全满足的情况下最小二乘估计及部分渐近性质与非线性程度度量。
1 泛一列非线性回归模型的LS估计
在一般的回归模型理论研究中, 研究者总是假设其随机扰动项是等方差且不相关的, 即。尽管在许多情况下, 这个假设可以认为基本上成立, 但在有些情况下对所获得的数据经过误差分析后会发现, 这些假设具有明显的不适宜性, 它们误差的方差可能是互异的[1–2], 也可能是彼此相关的,这时误差向量的协方差矩阵, 此处是一个正定矩阵, 它也可能包含有未知参数, 暂考虑其没有未知参数的情形。
下面考虑非Gauss-Markov条件误差项的非线性回归模型的估计及部分渐进性质, 并考虑带约束条件情形[3]。
考虑模型


此即模型(2)的参数估计, 这里为前面所描述的参数向量。
另外, 上述结果还具有渐近最小方差[4], 具体证明过程略。
2 带线性约束条件的LS估计

对于模型(1), 若约束条件为较为一般的情形, 也可以使用加号逆或带约束条件的广义逆, 得到其唯一存在的LS估计

3 两类非线性回归模型的岭估计
前面研究的LS估计结果具有无偏性, 这里综合考虑估计的均方误差(方差和偏差)。事实上, LS估计尽管满足无偏性, 但有时其方差部分却很大, 最终导致其均方误差较大。此外, 模型(1)和(2)中要求列满秩, 但事实上矩阵可能存在复共线性等不满秩状况, 这会使得LS估计与实际拟合状况差距很大。考虑放弃估计的无偏性, 在有偏估计中大幅度降低方差并最终降低其均方误差, 并从矩阵主对角占优的思路出发, 考虑矩阵不满秩情形, 为此, 引进岭参数(或称偏参数)。
对模型(1):

。 (7)
其中> 0, 称上述结果为岭估计。= 0的情形即为普通的LS估计。事实上, 总存在> 0使得有较小的均方误差(当时), 从而在均方误差意义下, 岭估计优于LS估计。实际上, 通过对的选取,可以让估计趋于渐近无偏。
在实际应用中, 岭参数的选择是一个根本性的问题。目前应用的较为普遍的有Hoerl–Kennard公式法及岭迹法等, 在一般的SPSS或SAS统计软件中都有相关的计算程序, 本文不再赘述。
4 部分泛二次非线性回归模型
考虑模型
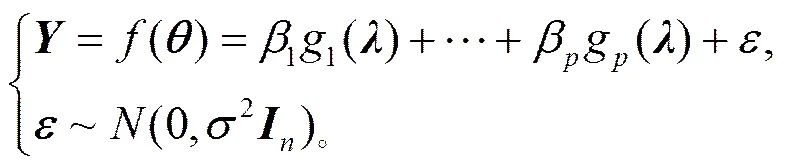
定义1 称

为模型(8)的局部曲率。
模拟研究显示, 有些模型计算出来的参数效应曲率尽管非常大, 但其本身的非线性程度并不强, 所以很多学者考虑实施参数变换试图降低参数效应曲率, 但都没有好的进展[7]。而这里计算出来的局部曲率反应的是该模型的固有曲率, 体现其本身的非线性程度。在迭代过程中, 可以使用作为新的下一轮迭代值, 从而提高收敛速度[6–7]。易证如下定理。
深度学习的飞速发展为现代农业的进步带来了新的契机,深度学习技术与农业物联网技术的结合可以为植物提供更加适宜的生长环境。深度学习技术能根据大量的历史信息和实时数据对未来进行合理的推断。物联网技术和深度学习技术相辅相成。物联网技术为深度学习提供持续的数据需求,深度学习技术可以处理和从中学习的数据越多,其预测的准确率也会越高。
定理2 模型参数变换不改变模型(8)中局部曲率的值。
该定理进一步说明了对于参数效应曲率而言在度量非线性程度时具有的优势。下面详细研究部分泛二次非线性回归模型的参数效应曲率。
定义2 模型(8)的参数效应曲率为

, (11)
这里是任意的。该曲率反映了回归模型非线性程度最强的方向。
给定方向向量, 有

必须指出的是, 模拟研究表明, 上述参数效应曲率描述模型(8)的非线性程度没有局部曲率(9)的实际效果好。
参考文献:
[1] 赵慧秀. 带有线性约束的指数族非线性回归模型置信域的曲率表示[J]. 曲阜师范大学学报, 2010, 36(1): 38–40.
[2] Williams E J. Exact fiducial limits in nonlinear estimation [J]. J R Statistic Soc, 1962, 1324: 125–139
[3] 曹建胜, 黄炳家, 傅少川. 带约束条件的矩阵最佳逼近[J]. 山东科学, 1996, 9(2): 8–11.
[4] 邢进良. 一元非线性回归方程的模型及应用[J]. 襄樊学院学报: 自然科学版, 2007,28(8): 18–21.
[5] 肖兵. 部分非线性回归模型的非线性度量[J]. 湖南文理学院学报: 自然科学版, 2013, 25(1): 10–13.
[6] 肖兵. 一列非线性回归模型的LS估计[J]. 常德师范学院学报: 自然科学版, 2001, 13(4): 6–7.
[7] 肖兵. 一列非线性回归模型的非线性度量[J]. 常德师范学院学报: 自然科学版, 2002,14(4): 18–20.
[8] 程云鹏. 矩阵论[M]. 西安: 西北工业大学出版社, 2000: 307–327.
(责任编校:刘刚毅)
The LSE and measure of non-linearity of some special nonlinear model
Xiao Bing
(Department of Mathematics and Computational Science, Hunan University of Arts and Science, Changde 415000, China)
First, the least squares estimator with extend case is studied, and its convergence is proven. Second, the mode to non Gauss-Markov condition is extended. The estimate property of a more generalized separated nonlinear model is discussed. At last, the method of iterative initial value selectionare studied, and a new trend for the method to measure the model’s non-linearity is given.
measure of non-linearity; separated; local curvature; the least squares estimator
10.3969/j.issn.1672–6146.2015.02.009
O 212.1
1672–6146(2015)02–0026–04
肖兵, xiaobing71@163.com。
2014–12–15
湖南省自然科学基金资助项目(12JJ6004), 湖南省科技厅项目(2011ZK3160)。
