基于因素分布模型的微震定位精度敏感性分析
2015-10-13高永涛吴庆良吴顺川杨凯豆丽萍姚鹏飞
高永涛,吴庆良,吴顺川,杨凯,豆丽萍,姚鹏飞
基于因素分布模型的微震定位精度敏感性分析
高永涛,吴庆良,吴顺川,杨凯,豆丽萍,姚鹏飞
(北京科技大学土木与环境工程学院,金属矿山高效开采与安全教育部重点实验室,北京,100083)
根据微震定位方程,基于误差最小原理,构造微震定位精度敏感性评价的输入输出数学模型,选取震源点到各检波器之间距离测量误差、微震波波速标定误差和信号到时拾取误差3个影响因素作为分析因子。从信息熵的角度,分析因素分布密度函数,并通过泛函变分求得相应表达式。采用正交法设计16组方案,根据分布函数求取因素各水平值,进行全局敏感性分析。研究结果表明:3个因子取值在给定区间内均符合均匀分布;无论是对内场震源点还是外场震源点,微震波波速误差,是对定位结果影响最大的因素,各因子对定位精度影响的主次顺序为:e,e,e;对于内场震源点,3个因素对定位精度均有高度显著影响。但对于外场震源点,可能由于因素之间的交互作用或者试验误差影响,仅微震波波速标定误差对定位精度有高度显著影响。相关研究可为微震监测的准确定位等提供针对性指导。
微震;定位精度;敏感性;分布模型;误差
随着深部矿产资源的采掘和地下空间的开发利用,地下工程不断走向深部,特别是非煤矿山及隧道工程,高应力条件下岩爆、地质缺陷活化等问题日渐突出,单纯靠传统的岩石力学手段已经远远不能满足现实安全监测的需要,基于地球物理学发展起来的微震技术可以有效的监测岩石微破裂发生的位置,近年来,已经广泛地应用于矿山、水电等地下工程监测[1−3]。微震事件的空间分布规律包含着岩体不稳定区域的位置、范围和方向等大量信息,然而由于实际工程的复杂多样,造成定位结果会出现不同程度的误差,少则几米,多则数十米。影响微震定位精度的因素较多,且大部分具有随机性、可变性、模糊性等不确定特点,要进行准确可靠的定量分析较为困难,因此,对影响定位精度的根本因素进行敏感性分析十分必要。目前用于因素敏感性分析的方法很多,按考虑影响因素多少可分为单因素分析法(局部敏感性分析)和多因素分析法(全局敏感性分析)。单因素分析法只检验单个因素对模型的影响程度,计算简单快捷,但需要一定的假设,与实际情况不符,代表性的研究有Garson算 法[4]、随机检验法[5]等;而多因素分析法可检验多个因素对模型结果产生的总影响,并考虑了因素之间的相互作用对模型输出的影响,更符合实际情况,在桥 梁、结构、经济、水文、环境、生态等领域得到广泛应用[6−12],代表性的研究有方差分解法[10]、偏导数(PaD2)法[11],拉丁超立方单因子每次(LH-OAT)方 法[12]。由于敏感性分析在一定的输入输出模型和因素分布模型基础上进行的,因此,本文作者根据微震定位方程,基于误差最小原理构造相应的输入输出数学模型,并从信息熵的角度分析因素分布密度函数,最后采用正交设计法进行全局敏感性分析,找出相应的较敏感因素和最敏感因素。本文作者的研究可为微震监测的准确定位等提供针对性指导。
1 输入输出模型的建立

若发震时间为0,检波器接收到信号的时间为,震源到各检波器之间岩层中的微震波传播速度(均匀速度模型)为,则定位方程为
从式(2)可以看出:矿山现场地质地形复杂、资源开采时人类活动干扰等原因对微震事件定位精度的影响最终体现在3个方面:震源点到各检波器之间距离的测量误差(即检波器坐标测量误差)、微震波波速标定误差、信号到时拾取误差。假定参数测量值与真值之间误差为(=1, 2, …,;=1, 2, 3),则
将式(3)代入定位方程可得:
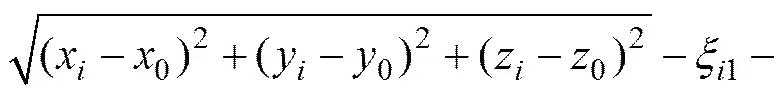
(4)
2 影响因素分布密度函数
为分析微震定位精度对相关参数的敏感程度,选取震源点到各检波器之间的距离测量误差D、微震波波速标定误差V和信号到时拾取误差T这3个因素作为分析因子。假定在某次微震事件定位分析过程中,某个因子值有种可能,且它们出现的概率分别为,则这个因子的熵为
若测量误差值有无穷多个可能,且连续分布,则熵可写为

求极限可得
假定某个因子只可能出现在有限区域[,]内,则限制条件记为。由于事先无法准确预测该因子取值,即不确定性最大,则对应的熵应为极值,对熵变分,则有。
定义函数
使其满足欧拉方程
通过限制条件,求得
显然某个因子取值在给定区间内符合均匀分布,式(13)为均匀分布的一般表达式。
3 因子各水平取值及试验方案的优化设计
在全局敏感性分析中,若对每个因素的每个水平都相互搭配进行全面分析,则随着因素和水平数的增加,处理组合数将急剧增加,必然会耗费大量的时间、人力和物力。大量研究表明:在全部处理组合中,采用正交设计方法,仅挑选部分有代表性的水平组合(处理组合)进行分析,同样能达到理想结果。
若某个因子值的分布区间为[,],分布密度函数为,选取个水平将该分布密度函数曲线下的全部面积做−1等分,算上头尾区间,则相应的积分上限即为各水平值,即
采用3因素4水平L16(45)进行正交设计。正交试验设计方案如表1所示。

表1 正交试验设计方案
4 算例分析
假定在空间区域内,6个传感器位于球体的6个方位点,坐标(单位均为m)分别是(0,500,500),(500,0,500),(1 000,500,500),(500,1 000,500),(500,500,1 000)和(500,500,0)。假定微震源(232,604,746)和(673,700,1 200)分别位于检波器阵列的内、外场区域,微震波在介质中传播的等效波速=5.2 m/ms,发震时间统一为某日10:00:00:20,传感器与震源空间分布位置如图1所示,本文规定在某1次微震事件中,外界对单一因素造成的误差相等。
选用北京科技大学自主研发的微地震监测系统(BMS)作为监测设备,对河北某矿山进行1 a多的微震监测[13]统计发现,震源点到各检波器之间的距离测量误差D(m)、微震波波速标定误差V(m/ms)和信号到时拾取误差T(ms)这3个因子的分布区间分别为[0, 6],和[0, 3],参照因素各水平的求解方法和正交试验方案,可得内、外场震源点的3因素4水平值如表2所示。

图1 传感器与震源空间分布位置示意图
最终求得内、外场震源点的定位结果(各16组),如表3所示。
5 敏感性分析
根据表3所示的定位结果,分别采用直观分析方法和方差分析法对影响微震定位精度的3个因素进行敏感性分析。设试验次数为,每个因素的水平数为个,每个水平作/(即次)试验。
5.1 直观分析(极差分析)
表4所示为内场震源点试验结果的极差分析,表5所示为外场震源点试验结果的极差分析。表4和表5中:K为第列因素水平所对应的试验指标的和;为K的平均值;R为第列因素的极差,反映了第列因素的水平变动时,定位精度的变动幅度。根据极差R,可以判断因素的主次。
从表4和表5可知:各列的极差不相等,这说明各因素的水平改变对定位精度的影响不相同,R越大,表示该列因素的数值在试验范围内的变化会导致定位精度在数值上变化越大,所以,极差最大的那1列即微震波波速误差,对定位结果影响最大的因素,也就是最主要的因素。由于内场和外场震源点试验结果的极差R从大到小的顺序均为V,T,D,故各因素从主到次的顺序为:V,T,D。
相对各因子列(第1,2和3列),空白列(第4列)的水平均值随着水平数的改变而变化(变化很小),说明因素之间有一定的交互作用,或试验有一定的试验误差影响(外场震源定位结果较为明显)。但由于其极差小于各因素列的极差,故而本算例中暂不考虑其影响。

表2 正交设计时内、外场震源点的3因素4水平值
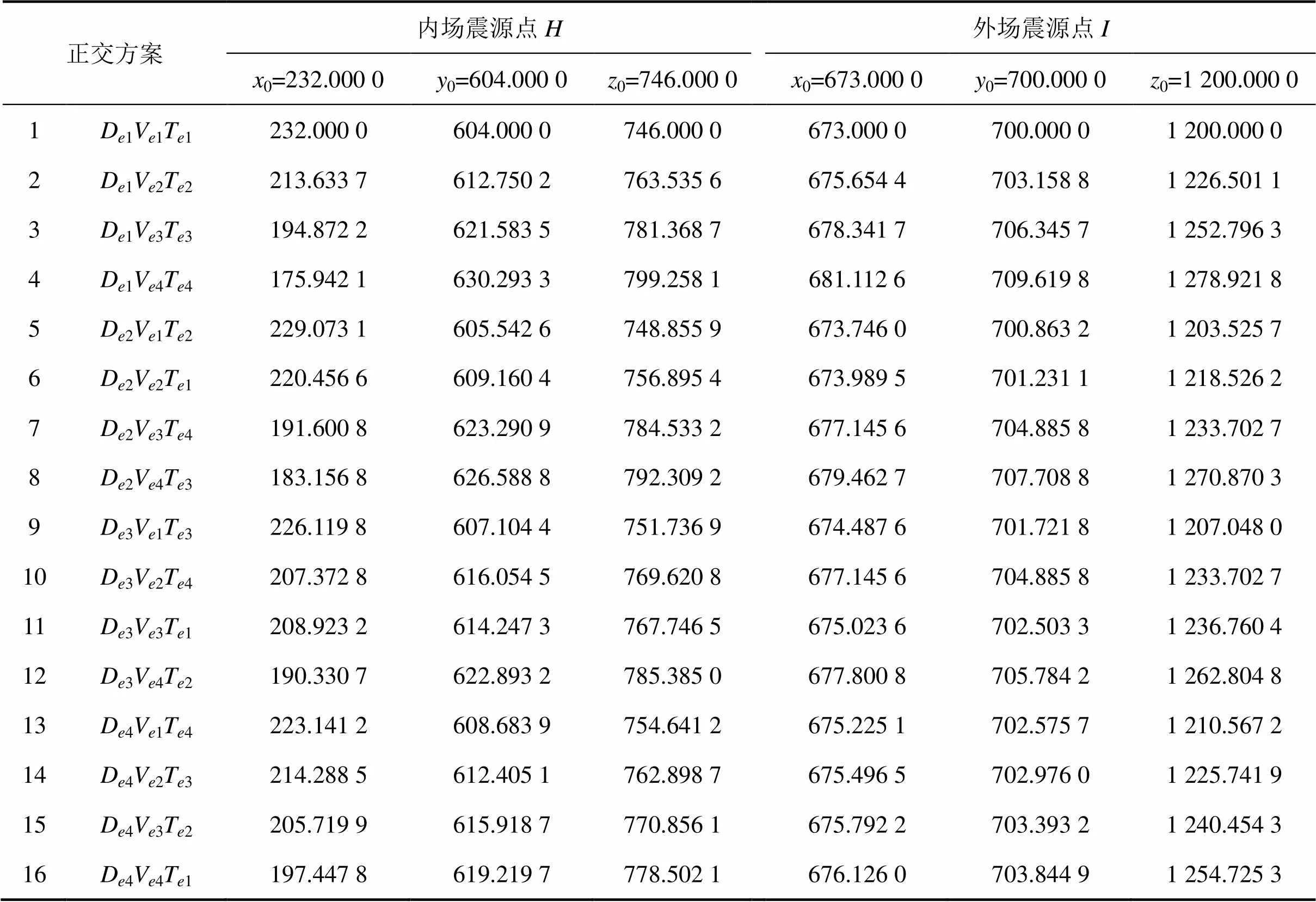
表3 内、外场震源点的定位结果

表4 内场震源点试验结果的极差分析
