考虑转子磁场谐波的永磁同步电机双闭环非线性建模分析

左曙光，高丽华，孟姝，马琮淦，谭钦文



考虑转子磁场谐波的永磁同步电机双闭环非线性建模分析

左曙光，高丽华，孟姝，马琮淦，谭钦文

(同济大学新能源汽车工程中心，上海，201804)

为分析转子磁场谐波对电磁转矩的影响，同时准确模拟电机动态运行工况，在推导考虑转子磁场谐波非线性数学模型的基础上，建立考虑转子磁场谐波的Simulink双闭环非线性仿真模型，并与开环模型进行对比分析。得到转子磁场谐波使得电磁转矩中出现6(∈N)阶谐波成分，和6阶以外的转速谐波成分。最后以目标电机为研究对象，进行动态高阶转矩试验测试。研究结果表明：该双闭环非线性模型的正确性，从而为电机动态运行工况下的转矩特性分析提供了一种准确、有效的建模方法。

永磁同步电机(PMSM)；磁场谐波；双闭环非线性；转矩波动

由于分布式电动汽车主要采用永磁同步电机(PMSM)直接驱动，其振动噪声问题呈现新的特点：永磁同步电机的转矩波动是车身阶次振动与车内噪声的主要振源，瞬态工况下对整车纵向振动的影响尤为显著[1−3]。由于电动汽车具有多工况、变负载、宽调速范围等特点，电动车用永磁同步电机谐波转矩更丰富和复杂，减振降噪难度更大。因此，对永磁同步电机动态转矩波动进行研究具有重要意义。永磁同步电机因具有效率高、转矩密度大、调速范围宽等优点，在电机功率密度、运行效率要求都非常高的领域得到了快速发展和广泛应用。然而永磁同步电机的自身特性决定了它不可避免地存在转矩波动，这也是其应用方面的主要缺陷[4−5]。产生转矩波动的主要原因[6]有电磁转矩波动、定转子齿槽定位转矩、绕组换相引起的转矩波动。其中，王兴华等[6]对换相引起的转矩波动进行了深入探讨；宋伟等[7−8]对定转子齿槽定位转矩已经进行深入研究，然而对电磁转矩波动的研究相对较少，而在分布式电动汽车中，常采用表贴式永磁同步电机，使得转子磁场谐波的影响较大，引起的转矩波动从电机设计角度无法消除，只能进行磁场优化，使其尽可能接近正弦分布，减小谐波分量[9]；莫会成等[10−11]从理论分析了产生转矩波动的原因，但没有建立仿真模型；Romeral等[12]建立了有限元模型却仅对高次谐波成分进行分析；李景灿等[13]在建立电机模型时，考虑到其内部因素的影响，尤其是转子磁场谐波的作用，并采用Simulink模型进行输出特性分析，但建立的是开环模型，并没有考虑到电机的控制系统和电机起动、加速等动态运行过程。为此，在建立电机模型时，不仅要考虑转子磁场谐波的影响，还要反映电机的动态运行过程。本文作者在考虑转子磁场谐波的基础上，建立基于矢量控制的Simulink双闭环(电流环和转速环)非线性电机模型，并对转速和电磁转矩进行仿真分析，通过对比基于矢量控制的电机动态高阶转矩测试试验结果，验证所建模型的正确性和有效性。

1 考虑转子磁场谐波的PMSM双闭环非线性仿真建模

1.1 PMSM线性数学建模

永磁同步电机−轴数学模型[9,13−14]为

转矩表达式为

机械运动方程为

式中：为电压；为电流；为磁链；下标和分别为和轴分量；md为互感；L和L为和轴电感；f永磁体等效励磁电流；f为永磁体产生的磁链；为转动惯量；R为阻力系数；L为负载转矩；em为电磁转矩；为电角速度；为机械角速度。

上述数学建模是目前常用的电机建模方法，是一种线性模型，它认为转子磁场在气隙中是理想的正弦分布[9]。

1.2 考虑转子磁场谐波的PMSM非线性数学建模

实际中，永磁同步电机由于永磁体制造及工艺上的限制，永磁体产生的转子磁场谐波分量很大，转子磁场并不是理想正弦分布[13]。因而需要建立一种考虑转子磁场谐波的永磁同步电机非线性数学模型。

此时转子磁场在气隙中的分布经过傅里叶变换得到

式中：为轴与相轴线的电角度。

永磁体基波及各次谐波在定子电枢绕组中产生的磁链表达式如下。

永磁体对相的感应磁链为

式中：1为永磁体产生的基波磁链，3，5，…为各次谐波磁链。所以，此时和轴的磁链为：

此可建立考虑转子磁场谐波的电压平衡方程：

考虑转子磁场谐波的电磁转矩方程：

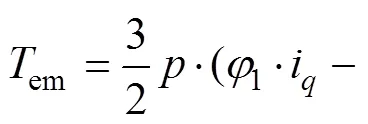
1.3 基于MATLAB/Simulink的PMSM双闭环非线性仿真建模

若不考虑电机的控制系统，则可以建立考虑转子磁场谐波的开环模型，它只能够模拟电机的稳定运行工况。仿真流程如图1所示。图1中虚线框内的流程为不考虑转子谐波磁场时的电机建模方法。

图1 开环模型仿真流程图

本文在此开环模型的基础上，根据电机的实际运行，考虑到电机的控制系统和起动、加速等动态运行工况，建立双闭环(电流环和转速环)非线性仿真模型。

电流环是指采用电机矢量控制i=0的控制方式。并利用脉宽调制(PWM)电压逆变器完成电机模型的电流环回路。这种控制方式可以通过控制电机的电枢电流实现电机的电磁力矩控制，控制效率高，是表贴式永磁同步电机常采用的控制方法[15]。

转速环是指采用比例积分(PI)速度调节器完成对电机转速的控制。这种控制方式可以考虑电机转速变化时对电磁转矩的影响，从而准确模拟电机的动态运行过程。

双闭环非线性仿真流程如图2所示。从图2可见：将参考转速和仿真转速的差输入到PI调节器中，得到电流i，将i=0和i输入到派克逆变换模块中，得到三相参考电流，其与三相电流仿真结果输入PWM逆变器模块中得到三相电压，经过派克变换，得到u和u，将理论推导中的电压谐波成分叠加到电压模块中，得到新的u和u加载到电机的数学模型上，得到最终的仿真电流、仿真转速和仿真转矩。

图2 双闭环非线性仿真模型流程图

2 PMSM双闭环非线性模型与开环模型仿真结果对比分析

为验证双闭环非线性模型的优越性和有效性，进行仿真模拟。使用基于MATLAB/Simulink的PMSM双闭环非线性仿真模型对某1台PMSM进行仿真计算，求解器为ode4，PWM载波频率为10 kHz，仿真时间为10 s，步长为20 μs，参考转速设定为100 r/min，所加负载为30 N∙m，通入的电压为12 V。电机的主要参数如表1所示。

PMSM双闭环非线性模型与开环模型的电磁转矩对比如图3所示。

表1 永磁同步电机参数

(a) 双闭环非线性模型；(b) 开环模型

由图3可知：双闭环非线性模型能够模拟电机的动态运行工况，前5 s内电磁转矩波动比较剧烈，表明此时电机处于起步或加速等的状态。而开环模型只能模拟电机的稳定运行工况。此外，2种模型在5 s之后的稳定状态下，转矩都并非保持30 N∙m，而是在25~35 N∙m范围内呈周期性波动。

为了更好地分析电磁转矩谐波成分，取双闭环非线性模型与开环模型最后1 s稳定状态下的电磁转矩进行阶次特性分析。两者对比如图4所示。

图4 电磁转矩阶次对比图

从图4可见：字符表示转矩。根据电磁转矩6阶谐波频率计算表达式

式中：表示转速；为极对数。图4所示的双闭环非线性模型和开环模型中均出现了公式推导的6(∈N)阶谐波成分，如：6阶、12阶、18阶和24阶成分，其中6阶和12阶能量较高，为主要频率成分，18阶能量和24阶能量较低。

2.2 PMSM双闭环非线性模型与开环模型转速结果对比分析

以“三集中”改革推动乡村振兴的路径研究(赵勤学等） ................................................................................8-39

从图4可知：双闭环非线性模型仿真中的电磁转矩除永磁体引起的6(∈N)阶谐波外，还产生了其他的阶次成分，如图4所示的①，②和③阶，而这些阶次成分在开环模型仿真中并没有出现。为了确定双闭环非线性模型电磁转矩结果中的6(∈N)阶以外的谐波成分是否为转速阶次，对该工况下的转速进行 分析。

PMSM双闭环非线性模型与开环模型的转速如图5所示。

(a) 双闭环非线性模型；(b) 开环模型

由图5可知：双闭环非线性模型模拟的是电机的动态运行工况，转速由0 r/min开始加速5 s后最终达到稳定波动，而开环模型只能模拟电机稳定时的转速情况。

为了更好地分析转速对电磁转矩的影响，取双闭环非线性模型与开环模型最后1 s稳定状态下的转速进行阶次特性分析。两者对比如图6所示。

图6 转速阶次对比图

从图6分析可知：仿真中的转速也具有一定的阶次特性，电磁转矩与电机机械角速度之间存在一定的关系，且其传递函数为

且转速谐波与转矩谐波具有相同的频率成分[14]。从而确定，双闭环非线性模型电磁转矩结果中的6(∈N)阶以外的谐波成分如①，②和③阶为转速谐波。但由于开环模型中并没有转速环，不能体现转速阶次谐波对电磁转矩的影响，因而没有6(∈N)阶以外的转速谐波成分。

由图4可知：转速的阶次能量要比转矩的阶次能量要高，而这种现象是由于式(14)中的传递函数具有放大作用导致的。

通过将双闭环非线性模型与开环模型的电磁转矩和转速结果进行对比，可以得到以下结论。

1) 双闭环非线性模型能够模拟电机起动、加速、减速等瞬态工况，而开环模型只能模拟电机的稳定运行工况。

2) 双闭环非线性模型能够准确得到转子磁场谐波对电磁转矩的影响，除了转矩中存在6(∈N)阶的转矩谐波成分，还存在6(∈N)阶以外的转速阶次谐波成分。

3) 双闭环非线性模型增加了控制系统，从而易于实现对电机的动态实时控制。

3 动态高阶转矩测试试验验证

3.1 动态高阶转矩测试试验

转矩测量试验设备如图7所示，包括数据采集系统、测功机、转矩传感器、永磁同步电动机和电机控制系统。测功机对电机施加负载，电机控制系统控制电机转速，转矩传感器和数据采集系统分别进行转矩测量和数据采集。

图7 转矩测量试验设备

取试验中稳定工况下的电磁转矩进行研究，结果如图8所示。

图8 100 r/min下的试验转矩阶次图

从图8可见：试验中同样出现了转矩的6(∈N)阶谐波成分，除此之外还出现了6(∈N)阶以外的谐波成分，如图8中所示的①和②阶。为了确定其是否为转速阶次，对该工况下的转速进行阶次分析，结果如图9所示。

因为转速谐波会与电磁转矩谐波具有相同的频率成分[14]。由图9可知：转矩6(∈N)阶谐波以外的阶次成分为转速谐波。且转速的阶次能量要比电磁转矩的阶次能量要高。这与双闭环非线性模型的仿真结果相一致，从而验证了仿真模型的正确性和有效性。

图9 试验转速阶次对比图

3.2 试验结果与双闭环非线性模型和开环模型仿真结果对比

将动态高阶转矩测试的电磁转矩试验结果与双闭环非线性模型和开环模型结果进行对比，电磁转矩阶次对比如图10所示。

图10 电磁转矩阶次对比图

从图10可以得到：

1) 试验结果与双闭环非线性模型仿真结果中均存在6(∈N)阶的转矩谐波成分，和6(∈N)阶以外的转速阶次谐波成分，且6阶转矩谐波、12阶的转矩谐波和6阶的转速谐波能量误差较小，在7%~15%之间。而开环模型只能够得到6(∈N)阶的转矩谐波成分。从而验证了双闭环非线性模型的正确性和有 效性。

2) 试验结果与双闭环非线性模型仿真结果中的12阶转速谐波、18阶转速谐波和18阶转矩谐波、24阶转矩谐波能量误差较大，是由测试系统本身的测量误差引起的。

4 结论

1) 得到了转子磁场谐波对电磁转矩的影响，同时验证了Simulink双闭环非线性仿真模型的优越性，此模型能够准确反映电机动态运行时的电磁转矩和转速特性。

2) 验证了考虑转子磁场谐波的Simulink双闭环非线性仿真模型的正确性和有效性。

3) 转矩中存在6(∈N)阶的转矩谐波成分和6(∈N)阶以外的转速阶次谐波成分。从而为准确分析永磁同步电机的运行特性奠定了基础。

[1] 孟姝. 永磁同步电机转矩波动及其对电动轮振动特性影响[D]. 上海: 同济大学汽车学院, 2013: 8−45. MENG Shu. Motor torque ripple and its influence of vibration characteristics of electric wheel[D]. Shanghai: Tongji University. School of Automotive Studies, 2013: 8−45.

[2] 马琮淦, 左曙光, 何吕昌, 等. 声子晶体与轮边驱动电动汽车振动噪声控制[J]. 材料导报, 2011, 25(8): 4−8. MA Conggan, ZUO Shuguang, HE Lüchang, et al. The phononic crystals and vibration noise control of electric vehicles with direct wheel drive system[J]. Materials Review, 2011, 25(8): 4−8.

[3] 王建, 张立军, 余卓平, 等.燃料电池轿车电机总成的振动阶次特征分析[J]. 汽车工程, 2009, 31(3): 219−223. WANG Jian, ZHANG Lijun, YU Zhuoping, et al. An analysis on the vibration order feature of the electric motor assembly in a fuel cell car[J]. Automotive Engineering, 2009, 31(3): 219−223.

[4] 罗宏浩, 廖自力.永磁电机齿槽转矩的谐波分析及最小化设计[J]. 电机与控制学报, 2010, 14(4): 30−40. LUO Honghao, LIAO Zili. Harmonic analysis and minimize design of permanent magnet motor cogging torque[J]. Electric Machines and Control, 2010, 14(4): 30−40.

[5] 于增亮. 轮毂电机驱动电动车悬架系统振动特性研究[D]. 上海: 同济大学汽车学院, 2010: 61−112. YU Zengliang. Vibration analysis of suspension system in four in-wheel-motor driven electric vehicle[D]. Shanghai: Tongji University. School of Automotive Studies, 2010: 61−112.

[6] 王兴华, 励庆孚, 王曙鸿. 永磁无刷直流电机负载磁场及其电磁转矩的计算[J]. 中国电机工程学报, 2003, 23(4): 140−144. WANG Xinghua, LI Qingfu, WANG Shuhong. Analytical calculation of loaded magnetic field and electrical magnetic torque in brushless DC motor[J]. Proceedings of the Chinese Society for Electrical Engineering, 2003, 23(4): 140−144.

[7] 宋伟, 王秀和, 杨玉波.削弱永磁电机齿槽转矩的一种新方法[J]. 电机与控制学报, 2004, 8(3): 214−217. SONG Wei, WANG Xiuhe, YANG Yubo. A new method to weaken permanent magnet motor cogging torque[J]. Electric Machines and Control, 2004, 8(3): 214−217.

[8] 杨玉波, 王秀和. 极弧系数组合优化的永磁电机齿槽转矩削弱方法[J]. 中国电机工程学报, 2007, 27(6): 7−10. YANG Yubo, WANG Xiuhe. Analysis of the optimization of the pole arc combination to reduce the cogging torque in PM motors[J]. Proceedings of the Chinese Society for Electrical Engineering, 2007, 27(6): 7−10.

[9] 唐任远. 现代永磁电机理论与设计[M]. 北京: 机械工业出版社, 1997: 85−89. TANG Renyuan. Modern permanent magnet synchronous machines[M]. Beijing: China Machine Press, 1997: 85−89.

[10] 莫会成.永磁交流伺服电动机转矩波动分析[J]. 微电机, 2007, 40(3): 1−4. MO Huicheng. Permanent magnet AC servo motor torque fluctuation analysis[J]. Micromotor, 2007, 40(3): 1−4.

[11] 杨顺昌, 廖勇, 余渝. 考虑谐波影响后交流励磁电动机电磁转矩分析与计算[J]. 电工技术学报, 2003, 18(1): 5−9. YANG Shunchang, LIAO Yong, YU Yu. Analysis and calculation of electromagnetic torque of AC excited motors incorporating the effect of harmonic currents in the excitation source[J]. Transactions of China Electrotechnical Society, 2003, 18(1): 5−9.

[12] Romeral L, Fabrega A, Cusido J, et al. Torque ripple reduction in a PMSM driven by direct torque control[C]// Power Electronics Specialists Conference (PESC). Greece: IEEE, 2008: 4745−4751.

[13] 李景灿, 廖勇. 考虑饱和及转子磁场谐波的永磁同步电机模型[J]. 中国电机工程学报, 2011, 31(3): 60−66. LI Jingcan, LIAO Yong. Model of permanent magnet synchronous motor considering saturation and rotor flux harmonics[J]. Proceedings of the Chinese Society for Electrical Engineering, 2011, 31(3): 60−66.

[14] QIAN Weizhe, Panda S K. Speed ripple minimization in PM synchronous motor using iterative learning control[J]. IEEE Transactions on Energy Conversion, 2005, 20(1): 53−61.

[15] 张秀峰. Maltab机电控制系统技术与应用[M]. 北京: 清华大学出版社, 2011: 209−240. ZHANG Xiufeng. Electromechanical control system technology and application[M]. Beijing: Tsinghua University Press, 2011: 209−240.

(编辑 罗金花)

Double closed-loop nonlinear modeling and analysis for permanent magnet synchronous motor considering rotor magnetic field harmonics

ZUO Shuguang, GAO Lihua, MENG Shu, MA Conggan, TAN Qinwen

(Clean Energy Automotive Engineering Center, Tongji University, Shanghai 201804, China)

In order to analyze the influence of rotor field harmonics on the electromagnetic torque, and accurately simulate the motor dynamic operating conditions, a double closed-loop nonlinear Simulink model was established based on the deduction of mathematical model accounting for rotor magnetic fieldharmonics. The model was also compared with the open-loop model. The results show that the 6(∈N) components of electromagnetic torque and rotational speed harmonics except 6come from the rotor magnetic fieldharmonics. Finally, high-order torque test was conducted for the target motor. The result shows that the established double closed-loop model is accurate and can help to analyze the dynamic torque characteristics.

permanent magnet synchronous motor (PMSM); magnetic field harmonics; double closed loop nonlinearity; torque fluctuation

10.11817/j.issn.1672-7207.2015.09.008

TM341；TM351

A

1672−7207(2015)09−3217−07

2014−12−13；

2015−02−20

国家自然科学基金资助项目(51375343)；重大科研仪器设备专项(2012YQ150256) (Project(51375343) supported by the National Natural Science Foundation of China; Project(2012YQ150256) supported by the National Major Scientific Instrument Equipment Project of China)

左曙光，教授，博士生导师，从事新能源电动汽车振动与噪声方面研究；E-mail: sgzuo@tongji.edu.cn