髋关节表面接触应力数学模型的建立及验证

王沫楠，安贤俊



髋关节表面接触应力数学模型的建立及验证

王沫楠，安贤俊

(哈尔滨理工大学 机器人研究所，黑龙江哈尔滨，150080)

基于体外实验的不可行性和有限元方法实现的复杂性，提出利用数学模型揭示髋关节表面接触应力与几何参数之间的关系进而模拟三维静态髋关节表面生物力学特性，并以此来研究人体髋关节表面的承载区域、应力分布以及接触应力峰值等属性。同时，利用有限元方法建立单足静立髋关节模型并进行模型分析，通过仿真结果与数学模型计算结果的对比，从髋关节表面接触应力分布和接触应力峰值2个方面对所建立的数学模型进行评价，验证数学模型的精确性和普适性。最后，利用髋关节表面接触应力数学模型对影响人体髋关节应力分布关键因素的量化分析，给出导致股骨头产生病变的病理因素。研究结果表明：在人体正常活动范围内，仿真结果与数学模型计算结果趋势与数值吻合度满足要求。

髋关节；接触应力；数学模型；模型验证；有限元法

髋关节是人体最大的负重关节，属于球窝结构，起着传导重力的作用。在人体众多活动关节中，髋关节是最稳定的关节，这使得人类能够完成较大范围的动作。我们也发现，髋关节是临床上最常见的多发病变关节，以髋关节发育不良而引起的关节炎为例，如果病理改变不能及时纠正，就会使髋臼脱离原来位置甚至造成脱位，不能以球窝状覆盖股骨头，关节表面负重面积减少，应力增大，且集中在髋臼外缘，从而导致髋关节骨性关节炎发生及加重[1−2]。因此，建立髋关节表面接触应力模拟模型，有助于及时发现患病关节病变状况，为治疗方案的确定提供重要的参考数据。髋关节生物力学特性研究方法主要有生物力学实验法[3−5]及各种数值分析方法[6]。长期以来，人体骨骼生物力学特性都是通过对离体骨骼的实验研究获取的。如Taylor等[7]指出在髋关节或臀肌肌肉的作用下，股骨内侧压应力与外侧张应力有着显著差别；阿良等[8]通过MTS试验机测试健康成人新鲜股骨标本，发现在纵向压缩、三点弯曲、轴向扭转状态下，股骨干在同等载荷时各个截面所承受的力学分布不同。通过力学实验获取骨骼生物力学特性方法在应用方面的限制在于无法获取个体活体组织的接触应力分布模型。为了模拟活体组织的生物力学行为，多数研究者采用数值分析的仿真方法，有限元法是应用最广泛的数值分析方法。有限元法起初应用在心血管系统的力学问题研究中，20世纪70年代开始应用于骨科生物力学研究[9]，80年代应用范围普及到人体各部分骨骼[10]。国外有很多先进的研究成果，如William[11]应用有限元法建立了腿部仿真模型；美国华盛顿大学人机交互技术实验室建立了快速有限元模型[12]。20世纪90年代末，国内出现一些利用有限元法分析组织性能的研究，有限元法通过仿真方法模拟人体组织生物力学特性，具有模型复杂，分析结果准确性高等优点，但是在计算速度方面不具优势，同时分析过程复杂、对操作者要求较高。综上所述，本文作者拟解决2个方面的问题：一是找到简便易行的专门患者髋关节表面接触应力模拟方法；二是验证利用该模拟方法表征髋关节表面接触应力的精确性。基于以上研究目标，本文作者提出通过建立精确三维静态髋关节接触应力数学模型，计算人体髋关节股骨头表面的承载区域、应力分布以及接触应力峰值等特性，从而揭示髋关节表面的力学特性与其几何参数之间关系的创新思路；提出利用有限元方法建立虚拟髋关节模型，对不同载荷下关节表面接触应力分布和接触应力峰值进行分析，将分析结果与数学模型计算结果进行对照，验证所构建接触应力数学模型的精确性和普适性的研究构想；同时，利用验证后的数学模型分析导致股骨头产生病变的病理因素，以便为临床治疗和髋关节假体制作等提供参考依据。

1 方法

1.1 髋关节表面接触应力数学模型的建立

1.1.1 建立坐标系

以右髋作为研究对象建立髋关节球面坐标系，将关节球面的球心置于坐标原点，和轴位于人体冠状面上，轴位于人体矢状面上。定义轴方向由身体右侧指向左侧，轴指向身体后侧，轴方向垂直向上。图1所示为所建立的髋关节模型坐标系，髋关节CE角如图2所示。

1.1.2 建立接触应力方程

因为骨与软骨之间存在组织液起到润滑作用，模型忽略摩擦力的影响，仅考虑压应力。此时，作用于关节球面上的切向应力为零，头臼间作用的合力就是径向压力。合力的作用点位于髋关节接触面上，方向指向球心。设关节面上任意一点的球面坐标为(，，)，合力作用点的球面坐标为(，，)，其中和为方位角，而和为极角，为球面半径。接触面上的合力与关节球面上任意一点的接触压应力之间满足以下积分关系式：

式中：d=2(sincos，sinsin，cos)sindd；=(sincos，sinsin，cos)。

1.1.3 压力与承载区域的确定

由于关节软骨的弹性模量与股骨和髋臼相比要小得多，将股骨头视为刚性球体，将髋臼视为刚性的半球壳，与股骨头同心，关节软骨位于二者中间。在髋关节上施加载荷后，关节软骨被挤压变薄，但是，由于在生理载荷下关节软骨的径向应变与股骨头半径相比要小得多，变形属于线弹性范围，将关节软骨看成是线弹性体。假设通过坐标原点且与载荷方向平行的方向线同髋臼半球面相交，根据理论力学原理可知，该交点与合力作用点重合，此时，关节球面上的最大应力max就是合力作用点上的接触应力p。由此关节面上任意1点的接触压应力与合力作用点上的接触压应力p满足以下线性关系：

式中：为接触面上任一点与合力作用点之间的圆心角。

在讨论股骨头表面承载区域之前要引入髋臼中心边缘角(central-edge angle，CE angle)的概念，它是股骨头中心点的垂线与髋臼外侧边缘的夹角，如图2所示。CE角是衡量髋关节接触面积的重要指标，接触面积随CE角的减小而减小。假设髋臼为规则的半球形凹面，则接触面积与CE角呈一次线性关系。

1.1.4 单足静立状态髋关节数学模型

在单足静立状态下，髋关节接触力在垂直于冠状面的分量仅为冠状面内合力的3%，可以忽略不 计[13]。所以髋关节接触力只有2个分量，即= (sin，0，cos)。规定角度，，，和CE从坐标系原点沿坐标轴正向看，绕坐标轴逆时针旋转的角度为正。将坐标轴进行旋转，使合力作用点位于关节球面的顶点上。则数学模型的积分关系在新建的坐标系下为：

，

完成上述积分，解得关节球面上合力作用点的接触压应力为

由上面的分析可知：当通过坐标原点且与载荷方向平行的方向线同髋臼半球面相交时，交点与关节球面的合力作用点重合，即关节面上的最大接触压应力就作用在该交点上，此时max=p；当通过坐标原点且与载荷方向平行的方向线同关节球面的交点落在接触球面之外时，合力不通过球心，关节球面上接触压应力峰值max取承载区域边缘上距该交点距离最近的点的应力，此时最大接触应力max满足方程(2)，即。

1.2 髋关节有限元模型及表面接触应力分析

1.2.1 数据导入

以全髋关节为研究对象，对正常成年男子进行螺旋CT扫描，扫描长度为346 mm，CT机扫描层间距为1.5 mm，获得的CT图片以DICOM格式输出并储存在计算机中。将DICOM格式的CT数据导入医学图像处理软件Mimics中，得到断层影像。

1.2.2 图像分割

CT图像导入Mimics以后，利用阈值设定来确定图像的编辑范围，再利用骨组织与软骨的灰度值差异将骨组织的数据提取出来，就可以实现最基本的分割。图像分割后，对图像中因扫描时出现的干扰数据进行修补和擦除，然后将其边缘修剪整齐，生成边界轮廓线，再将轮廓线以内的区域进行填充，从而得到较高精度的CT数据。

1.2.3 三维重建

对已分割出的2个部分进行三维重建，得到股骨和髋臼的三维模型。为了减少模型在导入Goemagic软件后产生的自相交和钉状物数量，在 FEA模块中对三维模型进行处理，从而达到光顺模型表面的目的。利用Mimics的角度测量功能可以对髋臼CE角进行测量。CE角为50°和10°的髋臼模型如图3所示。

θCE/(°)：(a) 50；(b) 10

1.2.4 关节软骨几何建模

由于软骨的灰度较小，在CT图像上无法清晰显示，不能利用CT图像对关节软骨进行三维重建。因此，假定关节软骨充满股骨头与髋臼之间的空隙，将所有冠状面上的髋关节CT影像中的头臼空隙填充，利用CMF/Simulation模块中的Boolean操作对模型进行布尔运算，股骨及髋臼模型被裁减出去，获得关节软骨的近似模型。CE角为40°的关节软骨模型如图4所示。

图4 关节软骨模型

1.2.5 有限元模型生成

首先，将生成的三维模型导入逆向工程三维检测软件Geomagic Studio 2012中，对模型进行修正优化，该软件可以根据导入模型的几何特征自动创建三角面片网格，并检测模型的不合格网格，用户可以通过手动操作对模型进行修改。将模型由多边形格式转换为点云格式，检查是否存在体外孤点，在确定点云合格后将其封装，完成对几何模型三角面片的优化。然后，通过用若干个不同大小、不同曲率的曲面片对模型进行拟合，最终的三维几何模型，以IGS格式保存，如图5所示。最后将股骨、关节软骨以及髋臼的IGS模型导入Unigraphics NX中进行装配，得到髋关节的装配模型，以IGS格式导出。装配后的髋关节模型如图6所示。

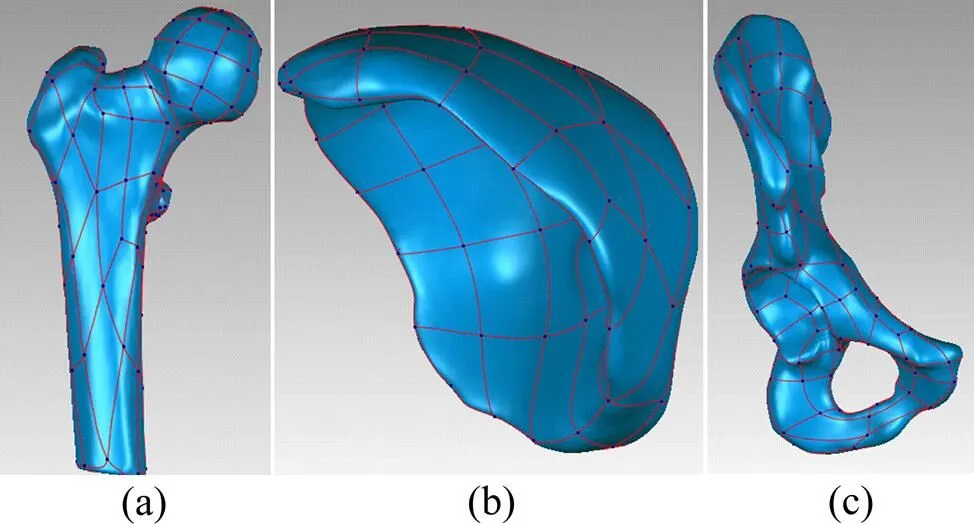
(a) 股骨；(b) 关节软骨；(c) 髋臼

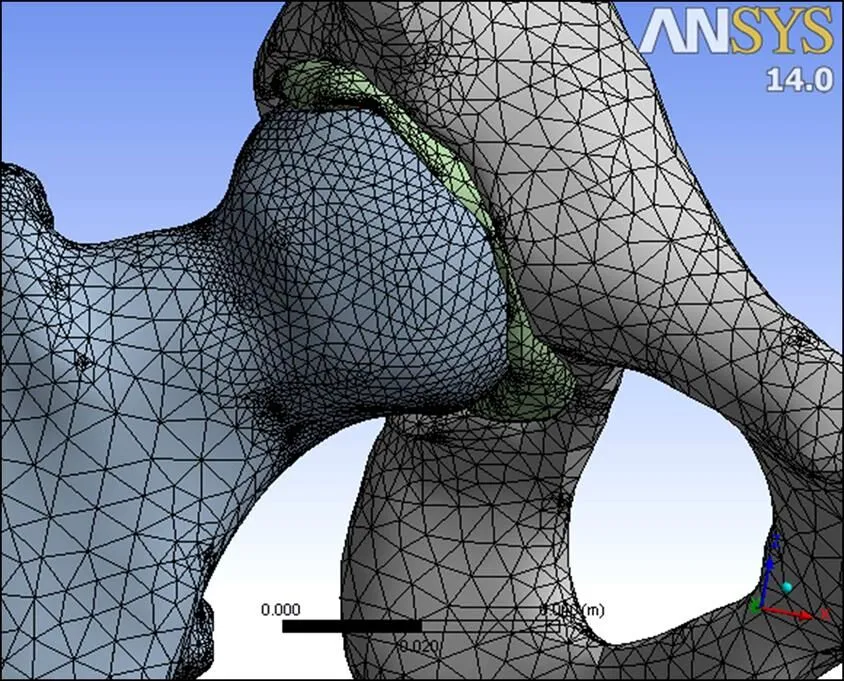
图6 髋关节装配模型

将已装配的IGS格式髋关节几何模型导入ANSYS 14.0中自动生成实体模型，在网格划分前，要先根据骨骼的材料特性设定合适的单元属性，这里定义皮质骨及关节软骨均为各向同性且连续均匀的弹性材料。定义皮质骨的弹性模量为17 300 MPa，泊松比为0.29；软骨的弹性模量为10 MPa，泊松比为0.4[14]。单元类型定义为10节点四面体实体单元(10solid187)，在设定好材料属性和单元类型后，对模型进行自动网格划分，为提高股骨头处的分析精度，对整个股骨头球体通过Remesh命令进行网格细化，得到最终的三维有限元模型。该模型单元总数为50 899，节点数为56 555，如图7所示。

图7 髋关节有限元模型

1.2.6 边界条件与载荷设定

三维有限元模型模拟单足站立状态，股骨远端被完全固定，髋臼与关节软骨被部分固定，只允许在冠状面上垂直方向移动。因单腿站立时髋关节接触力约为人体重力的3倍，设人体质量为70 kg，故加载于髋臼上的载荷大小为2 100 N，载荷方向位于平面内通过股骨头球心，角度根据髋关节模型的CE角 设定。

1.3 模型验证

为了验证髋关节表面接触应力数学模型，本研究建立了全髋关节的有限元模型，利用有限元分析法对髋关节进行表面接触应力仿真。分别获得有限元仿真模型表面应力分布和表面应力峰值，将此结果与通过数学模型计算获得的表面应力分布和表面应力峰值进行对比，给出对数学模型精确性的评价。

2 结果

2.1 改变作用力方向髋关节表面接触应力峰值分析结果

以CE=50°的髋关节作为研究对象，定义关节作用力方向从−40°~50°，仿真分析中每增加10°提取1个仿真结果，共10种工况，利用提取的仿真结果讨论改变关节作用力方向对股骨头表面应力分布的影响。通过有限元分析得到的不同关节作用力方向下的髋关节表面最大接触应力如表1所示。从表1可以看出：髋关节表面应力峰值随的增大而增大，且应力梯度逐渐增大，这与数学模型的计算结果一致。在=50°时，表面应力达到最大值6.626 7 MPa。

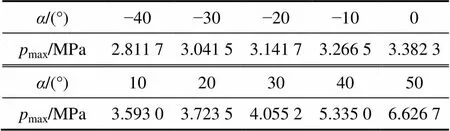
表1 不同关节作用力方向下的髋关节表面最大接触应力

2.2 不同CE角时髋关节表面接触应力峰值分析结果

设定载荷方向为=10°，加载于髋臼顶部，设定CE角从50°~10°递减，每次减少10°。以分析过程中提取仿真结果，依据仿真结果讨论CE角减小对股骨头表面应力的影响。通过有限元分析得到不同CE角的髋关节表面最大接触应力如表2所示。从表2可以看出：髋关节表面应力峰值变化趋势为随CE角的减小而逐渐增大，且CE角越小，应力峰值增大速度越快，在CE=10°时，达到最大值6.898 9 MPa。

表2 不同CE角的髋关节表面接触应力峰值

2.3 髋关节表面接触应力峰值综合分析结果

表3所示为通过有限元分析得到的不同CE角的髋关节生物力学模型在不同载荷方向下的髋关节表面最大接触应力。

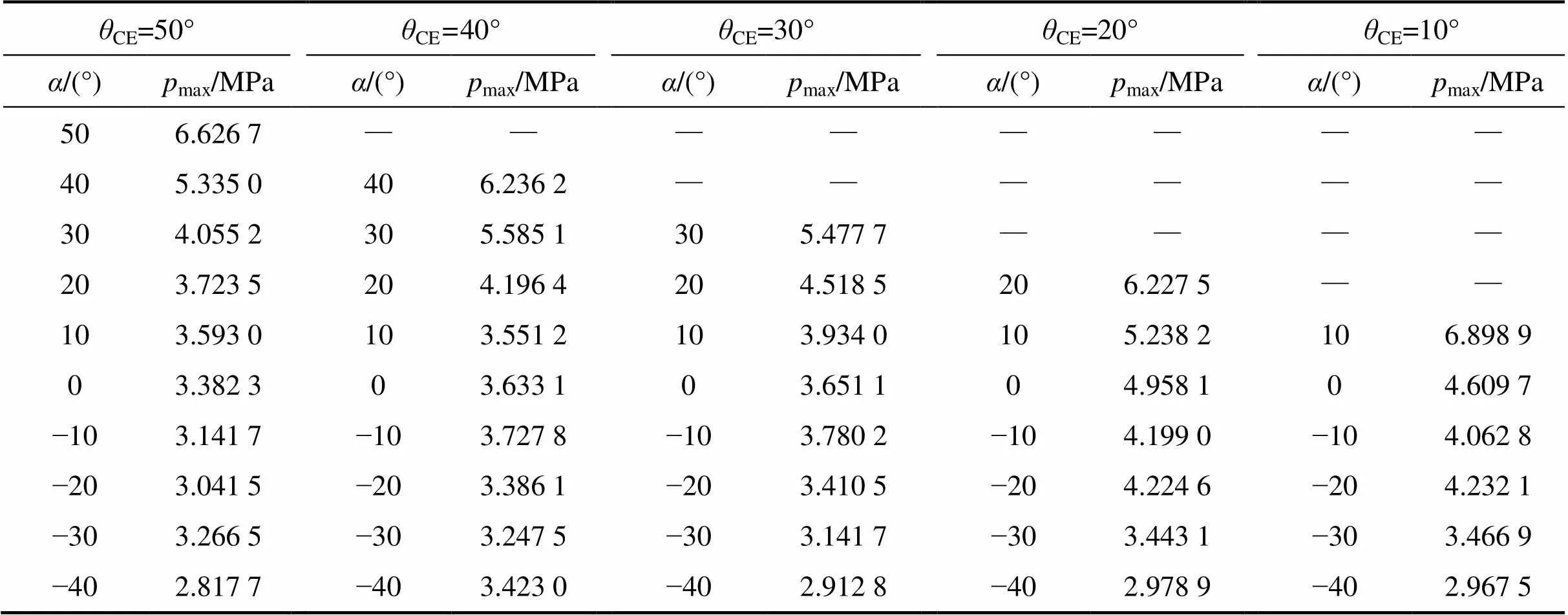
表3 不同CE角度的髋关节生物力学模型在不同载荷方向下髋关节表面接触应力峰值

图8所示为不同CE角的髋关节股骨头表面接触应力峰值随载荷方向的变化。其中通过有限元分析得到的数据用直线顺次连接，平滑的曲线代表数学模型的理论曲线。

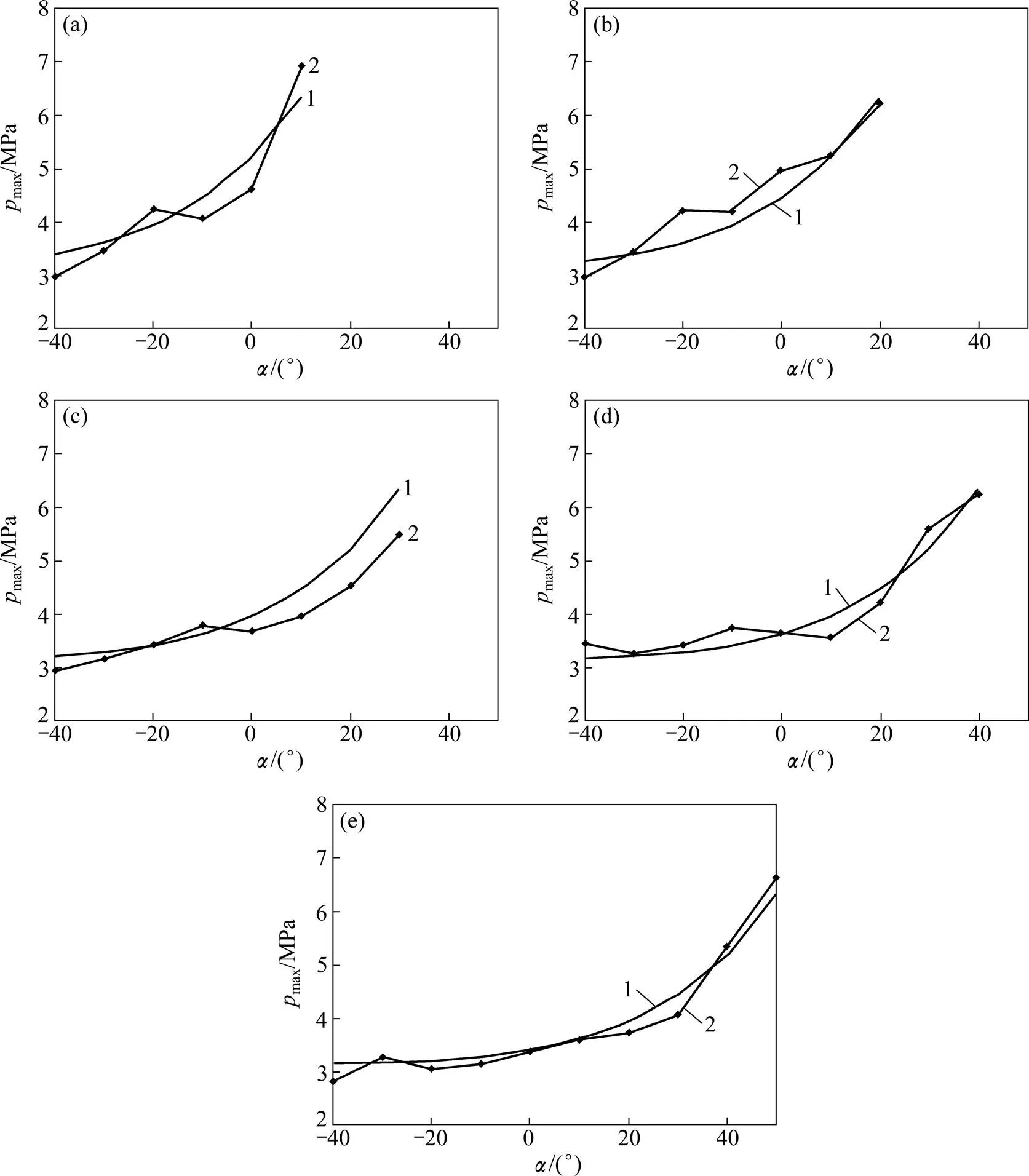
θCE/(°)：(a) 10；(b) 20；(c) 30；(d) 40；(e) 50

通过上述分析可以看出：对于不同CE角的髋关节，当CE−的差相等时，髋关节表面接触应力峰值分析结果相近，这个特征与力学模型的计算结果相吻合。同时，从数学模型计算结果与仿真结果对比曲线图可以看出，数学模型计算的理论曲线与有限元分析结果曲线无论从趋势还是数值上都比较相近，验证了本研究建立的数学模型的精确性。

2.4 髋关节表面接触应力分布

将不同方向的载荷分别加载到不同CE角的髋关节有限元模型上，得到髋关节表面的Von-Mises应力图，如图9所示。

(a)CE=50°，=0°时股骨头表面的应力分布；(b)CE=40°，=−30°时的应力分布；(c)CE=30°，=−40°时的应力分布；(d)CE=30°，=−50°时的应力分布；(e)CE=20°，=10°时的应力分布；(f)CE=10°，=−60°时的应力分布

图9 股骨头表面Von-Mises应力图

Fig. 9 Von-Mises stress maps of Femoral head surface

从图9(a)，(b)，(c)和(e)的分析结果可以看出：对不同CE角的髋关节有限元模型加载不同方向的载荷，股骨头表面的最大接触应力均发生在股骨头表面与载荷方向交点的附近，并以放射状向周边分布，从中心到周边逐渐减弱；当CE角为40°，=−30°时，应力峰值与CE角为30°，=−40°时的应力峰值相近，这与数学模型计算结果特性相互吻合。但通过图9(c)和图(d)的比较可以看出：CE角为30°，=−40°时的应力分布与=−50°时的应力分布差异不大；当=−50° 时，股骨头表面的应力峰值产生的位置也未有明显变化。当CE角为10°时增大载荷的偏转角度至−60°，如图10 (f)所示，股骨头表面应力集中分布在髋臼与股骨头的接触边缘。

3 讨论

3.1 髋关节表面接触应力数学模型表征生物力学特性

通过对式(4)单足静立髋关节接触应力数学模型的计算求解可知，影响人体髋关节头臼接触应力峰值的主要因素有髋关节球面的半径、接触合力、接触合力的方位角以及人体髋关节CE角CE。只要对这几个变量赋值，即可获得单足静立态时髋关节处的峰值应力、承载区域、应力分布等生物力学特性。通过数学模型计算得到髋关节表面接触应力分布特点表现为以下几点：

1) 当接触力不变时，关节面的承载区域面积和最大接触应力max随CE角的变化而变化。CE角越大，承载区域面积越大，max则越小；CE角越小，承载区域面积越小，max则越大。

2) 当CE角不变时，关节面上的承载面积和接触应力峰值max随关节作用力的倾斜角度的变化而变化。当合力作用点位于冠状面第一象限时，越大，承载区域面积越大，max则越小；越小，承载区域面积越小，max则越大。当合力作用点位于冠状面第二象限时，越大，承载区域面积越小，max则越大；越小，承载区域面积越大，max则越小。

3) 当合力的方向与承载区域外边缘所在平面垂直，即时，承载区域面积最大，覆盖关节球面的一半，此时最大接触压应力最小，。

4) 当合力作用点位于承载区域边界时，承载区域面积最小，近似看作一半圆弧，此时最大压力max最大，。

3.2 髋关节表面接触应力数学模型精确性评价

3.2.1 数学模型表征髋关节表面接触应力峰值精确性评价

1) 当CE为定值时，改变作用力方向即的大小，有限元分析结果表明：当从−40°到50°逐渐增大，此时，髋关节表面接触应力峰值随变化逐渐增大。数学模型计算结果也表明：当合力作用点位于冠状面第一象限时，越大，承载区域面积越大，max则越小；越小，承载区域面积越小，max则越大。当合力作用点位于冠状面第二象限时，越大，承载区域面积越小，max则越大；越小，承载区域面积越大，max则越小。

2) 当作用力方向即的大小固定，改变CE的大小。有限元分析结果表明髋关节表面应力峰值随CE增大而增大。这与数学模型计算结果一致。

3) 通过对髋关节表面接触应力峰值的综合分析，得到CE为10°，20°，30°，40°和50°共5组对比曲线，从对比曲线可以看出：髋关节表面接触应力数学模型计算的理论曲线与有限元分析结果曲线无论在趋势上还是数值上都比较接近，验证了髋关节表面接触应力数学模型的精确性以及在应用方面的普适性。

3.2.2 表征髋关节表面接触应力分布评价

从图9(a)，(b)，(c)和(e)的分析结果可以看出：对不同CE角的髋关节有限元模型加载不同方向的载荷，股骨头表面的最大接触应力均发生在股骨头表面与载荷方向交点的附近，并呈现出以放射状向周边逐渐减弱分布的特点。当CE角为40°，=−30°时，应力峰值与CE角为30°，=−40°时的应力峰值相近，这与数学模型计算结果特性相互吻合。但通过图9(c)和图9(d)的比较可以看出：CE角为30°，当=−40°时的应力分布与=−50°时的应力分布差异不大，=−50° 时，股骨头表面的应力峰值产生的位置也未有明显变化。当CE角为10°时增大载荷的偏转角度至−60°，如图9(f)所示，髋关节表面应力集中分布在髋臼与股骨头的接触边缘，这与本研究建立的数学模型计算结果差异较大。产生这种差异的原因是本文所构建的髋关节几何模型顶部厚，周边薄，使得股骨头顶部与关节软骨接触充分，而周边部分产生空隙；当逐渐加大载荷偏转角度到一定值时，载荷作用位置的关节囊开始产生空隙，使得股骨头表面与载荷方向交点不产生接触压应力，模型因关节囊的接触问题而失效，股骨头表面的应力集中在髋臼边缘与股骨头接触的位置。

3.3 髋关节表面接触应力数学模型的应用

图10所示为利用数学模型得到的不同CE角的髋关节股骨头表面接触应力峰值随载荷方向的变化情况。从图10可以看出：在人体正常的活动范围内(−20°＜＜10°)时，CE角越小，受力面积越小，股骨头表面接触应力峰值越大，且随载荷方向的变化而增大的速度越快。因髋臼发育不良引起的生物力学属性的变化主要表现为髋关节应力大幅度增加，负重面积减少，应力分布不均匀并集中于髋臼外缘。若髋关节长期在这种异常应力状态下活动，则将导致髋臼的负重面变浅。当髋臼倾斜增大到一定程度时，髋关节变得不再稳定，头臼匹配程度进一步降低，甚至导致髋关节脱位，使髋臼和股骨头由正常状态下的面面接触变为点面接触甚至点点接触，使髋关节的关节软骨局部反复承受过高的压应力载荷，超过髋关节软骨生理载荷限度，进而引起关节软骨变形、软骨下骨质硬化以及囊性变等退行性变[15−16]。

θCE/(°)：1—50；2—40；3—30；4—20；5—10

通过以上分析可知：对于患有髋关节发育不良(CE角小于20°)的患者，应尽量避免下肢在冠状面上的运动，因为髋关节在冠状面上的微小转动都可能导致接触表面应力的急剧变化。在手术方面，可以通过髋臼假体置换或添加髋关节外展支架的手段来提高髋臼的覆盖率，减小股骨头表面承受的应力。理论上CE角越大对髋关节的健康越有利，但具体手术方案要根据患者的具体情况综合考虑而定。

4 结论

1) 数学模型能正确反应髋关节表面应力分布情况。当载荷偏转角度α大于−40°时，数学模型计算结果和有限元模型分析结果相同条件下表现出相同的应力分布特征。当载荷偏转角度α小于−40°时，由于有限元模型的接触失效问题，导致两者间有较大偏差。通常人体正常的活动范围为−20°＜＜10°，所以，在此范围内数学模型能正确反应髋关节表面应力分布情况。

2) 数学模型能正确计算不同作用力方向、不同CE角度髋关节表面接触应力峰值。通过对CE为10°，20°，30°，40°和50°时不同作用力方向髋关节表面接触应力峰值的仿真结果和数学模型模拟结果的对比，得出两者在趋势和数值两方面都很接近。

3) 数学模型简便易行且满足精确性要求。利用髋关节表面接触应力数学模型模拟髋关节表面应力避免了有限元从建模到分析的复杂过程，而且在数值和趋势两方面都能满足临床精确性要求。实现了在不进行体外生物力学实验的前提下，利用简便易行的方法获取髋关节表面接触应力信息的目标。

4) 可以利用该数学模型进行髋关节表面接触应力分析，为临床应用提供参考。通过数学模型模拟的髋关节几何参数与表面接触应力关系曲线，为髋关节疾病治疗方案的制定和假体制造提供有价值的参考。

由于有限元模型的限制，没有对数学模型推导出的“当合力的方向与承载区域外边缘所在平面垂直时，股骨头表面接触应力峰值最小”结论进行验证。同时，本文在临床应用方面仅给出1个实例，数学模型在临床上的进一步应用还有待探讨。

[1] 肖海涛, 宋世锋, 郑南生, 等. 全髋关节置换术治疗晚期非创伤性股骨头缺血性坏死[J]. 现代生物医学进展, 2012, 27(12): 5291−5295. XIAO Haitao, SONG Shifeng, ZHENG Nansheng, et al. Total hip arthroplasty in the treatment of advanced non-traumatic osteonecrosis of femoral head[J]. Progress in Modern Biomedicine, 2012, 27(12): 5291−5295.

[2] 李蕊, 陈涛, 朴繁林, 等. 髋关节置换与运动性股骨头损伤[J]. 中国组织工程研究与临床康复, 2011, 15(48): 9078−9081. LI Rui, CHEN Tao, PIAO Fanlin, et al. Hip replacement and sports femoral head injury[J]. Journal of Clinical Rehabilitative Tissue Engineering Research, 2011, 15(48): 9078−9081.

[3] Rushfeldt P D, Mann R W, Harris W H. Improved techniques for measuring in vitro the geometry and pressure distribution in the human acetabulum II: Instrumented endoprosthesis measurements of articular surface pressure distribution[J]. Journal of Biomechanics, 1981(14): 315−323.

[4] Hodge W A, Fijan R S, Carlson K L, et al. Contact pressures in the human hip joint measured in vivo[J]. Proceedings of the National Academy of Sciences of the USA, 1986, 8(3): 2879−2883.

[5] Polliack A A, Sieh R C, Craig D D, et al. Scientific validation of two commercial pressure sensor systems for prosthetic socket fit[J]. Prosthet Orthot Int, 2000, 24(1): 63−73.

[6] Maxian T A, Brown T D, Pedersen D R, et al. 32 dimensional sliding/contact computational simulation of total hip wear[J]. Clin Orthop, 1996, 33(3): 41−50.

[7] Taylor W R, Roland E, Ploeg H, et al. Determination of orthotropic bone elastic constants using FEA and modal analysis[J]. Journal of Biomechanics, 2012, 35(3): 767−773.

[8] 阿良, 吉士俊, 范慈方. 有限元分析先天性髋关节半脱位及髋臼发育不良的应力变化[J]. 中华小儿外科杂志, 2000, 21(6): 327−330. A Liang, JI Shijun, FAN Cifang. Stress change of congenital subluxation of hip and dysplasia of acetabular by finite element analysis[J]. Chinese Journal of Pediatric Surgery, 2000, 21(6): 327−330.

[9] Felson D T. The epidemiology of osteoarthritis: Prevalence and risk factors[C]//Kuettner K E, Goldberg V M. Osteoarthritic disor2 ders. Rosemont, IL: American Academy of Orthopaedic Surgeons, 1995: 13−24.

[10] Cowin S C. The mechanics properties of cancellous bone[J]. In Bone Mechanics, 1989, 8(1): 30−57.

[11] William J L, Mary C P, Glimcher M J. Electron microscopic observations of bone tissue prepared anhydrously in organic solvents[J]. Journal of Ultrastructure Research, 1977, 59(2): 185−206.

[12] McGibbon C A, Krebs D E, Trahan C A, et al. Cartilage degeneration in relation to repetitive pressure: case study of a uniateral hip hemiarthroplasty patient[J]. J Arthroplasty, 2010, 14(1): 52−58.

[13] 芦俊鹏, 张建国. 人体颅脑三维有限元模型构建[J]. 微计算机信息, 2012, 22(8): 211−213. LU Junpeng, ZHANG Jianguo. A development of 3D FEM for cranium brain based on CT[J]. Microcomputer Information, 2012, 22(8): 211−213.

[14] 王天英, 姜福川, 王西十. 人体髋关节接触力计算分析一例[J]. 力学与实践, 2012, 27(2): 67−69. WANG Tianying, JIANG Fuchuan, WANG Xishi. Human hip contact force analysis[J]. Mechanics in Engineering, 2012, 27(2): 67−69.

[15] Silva M J, Keaveny T M, Hayes W C. Load sharing between the shell and centrum in the lumber vertebral body[J]. Spine, 2009, 22(2): 140−150.

[16] Hashimoto S , Nishi yama T, Hayashi S, et al. Role of p53 in human chondrocyte apoptosis in response to shear strain[J]. Arthritis Rheum, 2010, 60(8): 2340−2349.

(编辑 陈爱华)

Mathematics modeling and verification of hip joint surface contact stress

WANG Monan, AN Xianjun

(Robotics Institute, Harbin University of Science and Technology, Harbin 150080, China)

For patients, vitro experiment is not feasible and finite element method is more complex. 3D static hip joint biomechanical behaviors were expressed based on mathematics model between biomechanics and geometry parameter. Hip joint surface bearing area, stress distribution and peak contact stress were calculated from mathematical model. Then the same single static hip joint finite element model was developed and analysed. The results including femur surface stress distribution and peak contact stress from finite element simulation were compared to those from mathematical model in order to verify accuracy and universality mathematical model. Finally, femur pathologic mechanism was established based on the quantitative analyses results of mathematical model. The results show that the curve obtained from simulation is similar to the curve from mathematical model in trend and value.

hip joint; contact stress; mathematics modeling; model verification; finite element method

10.11817/j.issn.1672-7207.2015.06.015

TB12；R318.01

A

1672−7207(2015)06−2081−09

2014−06−13；

2014−08−20

教育部新世纪优秀人才支持计划(NCET-13-0756)；国家自然科学基金(61272387)；黑龙江省杰出青年基金(JC201302)(Prooject (NCET-13-0756) supported by the New Century Excellent Talents in University; Project (61272387) supported by the National Natural Science Foundation of China; Project (JC201302) supported by the Province in Heilongjiang Outstanding Youth Fund)

王沫楠，博士，教授，从事计算机辅助医疗研究；E-mail：qqwmnan@163.com