基于bagging−rough SVM集成的去马赛克方法

贾晓芬，赵佰亭，周孟然，陈兆权，黄贤波



基于bagging−rough SVM集成的去马赛克方法

贾晓芬，赵佰亭，周孟然，陈兆权，黄贤波

(安徽理工大学电气与信息工程学院，安徽淮南，232001)

能否有效保护图像的细节信息是衡量去马赛克技术优劣的关键因素，为改善图像细小边缘区域的边缘特征，抑制伪彩色效应或锯齿现象，提出一种基于bagging-rough的SVM集成算法，并利用该算法实现去马赛克。为提高支持向量机集成的预测精度，利用各平面之间的色彩相关性及色差恒定原理构建色差平面，在色差平面上利用图像的空间相关性构建原始样本集，采用bootstrap技术对原始样本集重取样，利用粗糙集约简算法约简重取样出的样本特征，然后用约简后的样本训练成员回归机、建立预测模型，将各成员回归机的预测结果采用均值法融合输出，其输出即为预测的色差平面上待插值点的色差，最后根据预测的色差值计算出丢失的像素值。仿真实验结果表明：所提去马赛克方法获得较优的客观指标彩色图像峰值信噪比(CPSNR)和S-CIELAB的色差，较好的保护图像的细节信息，达到较满意的视觉效果。

去马赛克；支持向量机；集成；粗糙集

数码相机作为一种利用电子传感器把光学影像转换成电子数据的彩色图像成像设备，获得1幅彩色图像需要3个传感器在每个像素点分别获取，和3种颜色分量。为了减小电子产品的体积，降低成本和复杂性，通常将彩色滤波阵列(CFA)覆盖在单传感器表面来同时获得3种颜色分量。因此，传感器阵列的每个像素点只能采集到1个颜色分量，为了得到1幅全彩色图像，每个像素点必须通过其相邻的已知颜色分量估计出该像素点丢失的另外2种颜色分量，这个过程被称为去马赛克。本文重点对最经典、应用最广泛的Bayer CFA[1]图像进行去马赛克的研究。传统的最邻近插值、线性插值等方法在平滑区域能取得较好的效果，但会降低图像的边缘特征，造成伪彩色效应或锯齿现象。近年来，各种获取高质量图像的方法，尤其是以获取高质量彩色图像为目标的去马赛克方法相继被提出，如应用稀疏表示的方法[2]、应用空间和色彩相关性的方法[3−4]、基于框架的方法[5]、基于图像修复艺术的方法[6]、基于异质性投影的方法[7−8]、利用自适应加权的方法[9]、利用支持向量机的方法[10]、基于边缘的方法[11]等。其中，利用支持向量机去马赛克是支持向量机在回归领域的重要应用，支持向量机可以按照可控制的精度逼近任一函数，具有全局最优、泛化能力强等优势，能够保证插值结果的准确性，但其稳定性有待提高。支持向量机集成(SVM ensemble)是一种新型的机器学习方法，是将集成学习应用于机器学习领域的产物。它不仅继承了支持向量机解决小样本、非线性、高维及局部极值等问题的优势[12]，而且稳定性、泛化能力均优于单个支持向量机。支持向量机集成因其出色的学习性能，已被应用在高分辨率遥感图像分类[13]、卫星图像分割[14]、混沌时间序列预测、微弱信号检测、故障诊断、雷达目标高分辨率一维距离像识别等领域，但将其应用于图像去马赛克方面的研究还较少见。为此，本文作者提出一种基于SVM集成的去马赛克方法，目的在于改善图像的细小边缘区域的边缘特征，减少结果图像中的伪彩色(虚假颜色)或锯齿现象，提高成像质量。

1 集成学习与粗糙集

1.1 集成学习

集成学习是通过训练多个成员学习机，并融合各学习机的结果而得到最终判别结果的学习方法。它能够显著提高学习机的泛化能力，被国际权威Dietterich称为当前机器学习领域的4大研究方向之一[15]，已广泛应用于机器学习、神经网络、统计学习等领域。如何生成集成个体和集成结果是集成学习的2个热点问题，集成个体具有的高精确度和高差异性[16]是获取良好集成结果的关键。鉴于此，bagging[17]，boosting[18]和AB[19]等集成方法相继被提出。

Bagging和boosting是在生成集成个体方面研究和使用最多的技术，但简单的bagging SVM和boosting SVM算法不能有效提高SVM的泛化能力。

1.2 粗糙集动态约简算法

粗糙集理论[20]是在经典集合论基础上发展起来的处理不确定、不一致信息的数学工具。对于大样本，支持向量机支持向量的数目众多，会使支持向量机所需训练时间和内存急剧增加。利用粗糙集方法约简掉训练样本中重要度较低的属性特征，可以有效降低训练样本的维数，缩短支持向量机的训练时间。粗糙集属性约简是以最小概率描述为准则来选择最优特征，每一个约简都包含有不同的属性，且具有与原始数据相近的分类能力，因此，利用多个约简结果训练的集成个体是准确且具有差异性的。

属性约简是粗糙集理论研究的核心问题之一，在机器学习领域已经被广泛研究。He等[21]利用邻域粗糙集选择SVM的样本及特征，大大缩减了SVM的训练时间和训练时占用的内存空间。Wang等[22]利用粗糙集的特征权重提高了SVM的分类能力。采用粗糙集约简算法去掉学习性能欠佳的特征子集，剔除冗余信息更有利于生成高精度和高差异性的个体[23]。显然，可利用粗糙集构造SVM集成的集成个体。因此，本文作者利用bagging和粗糙集构建成员回归机。

2 基于bagging-rough的SVM集成算法

为了提高成员回归机的精确度和差异性，利用bagging算法的bootstrap技术重取样本的原始样本集，再用粗糙集约简算法约简重取样出的样本特征，然后用约简后的样本训练并构建成员回归机，最后利用成员回归机预测待插值点的色差。该算法记为bagging-rough SVM集成算法，其步骤如下。

步骤1：对含有个样本的原始样本集采用bootstrap重采样技术获得组含有(＜)个样本的样本集，构成子系统集合={1，2，…，S}。其中：子系统S=(U,∪)是第(1，2，…，)组样本集；为样本集合；为待约简的特征属性集，为决策属性集合。

步骤2：对每一个子系统S，采用基于属性重要度的粗糙集相对约减算法进行属性约简。

步骤5：利用最终约简输出训练成员回归机，得到预测模型h。

步骤6：利用测试样本及训练好的成员回归机，预测待插值点的色差值，然后将各成员回归机预测的结果采用均值法融合输出，即。其中：为集成规模，即重采样的样本集的个数；为测试样本的输入样本；′为预测的色差值。

3 采用bagging-rough SVM集成的去马赛克方法

SVM集成法在用彩色图像各平面间的色彩相关性及色差恒定原理构建的色差平面上实现，在色差平面上用局部区域内的空间相关性原理构建原始样本集，然后用bagging-rough SVM集成法预测待插值点的色差值，最后计算出丢失的颜色分量。

采用SVM集成法去马赛克需要对，和3个平面分别插值，无论对那个平面插值都包括以下5部分：

1) 构建色差平面。根据彩色图像各平面间的色彩相关性及色差恒定原理构建色差平面K或K。

2) 构造原始样本集：在色差平面K或K上构造原始样本集={1，2，…，X}，其样本(=1，…，)，其中输入样本为7维向量，输出样本为1维向量。

在色差平面上，以每一个色差值为中心点的5×5区域构造2个样本。其输入样本分别利用该中心点的4个邻角(图1中的位置)或上、下、左、右(图1中的位置)的4个色差构造，即由4个色差、两两对角的色差之差、4个色差的均值组成7维向量；输出样本均是该中心点的色差。将上述方式构造的样本组成原始样本集={1，2，…，X}。

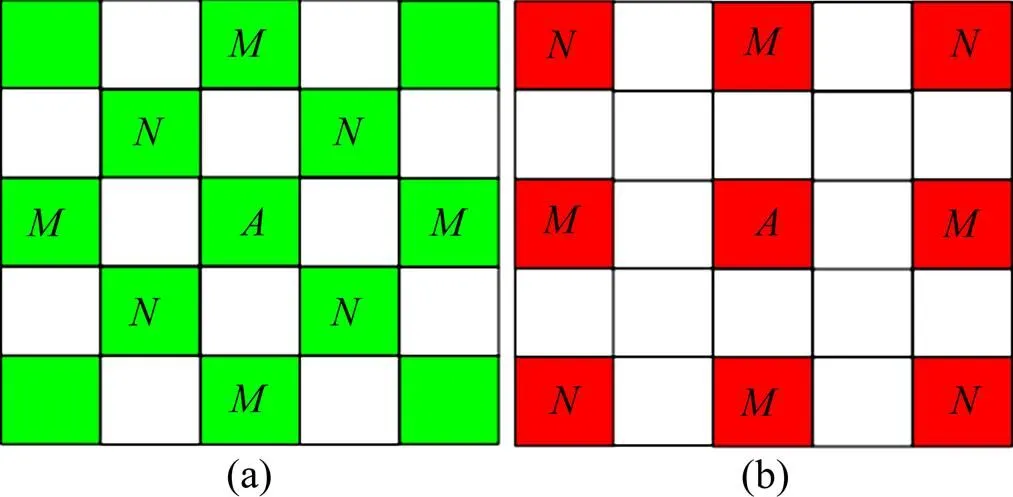
(a) 以G为中心点的5×5区域内G分布；(b) 以R为中心点的5×5区域内R分布

3) 构造测试样本。在色差平面上，以每一个待插值点为中心点，在其周围的3×3区域内构造一个测试样本。其输入样本是利用该中心点周围邻近的4个已知色差、其两两对角的色差之差、4个色差的均值构造的7维向量；输出样本′即为待预测的色差。

4) 利用bagging-rough SVM集成算法预测色差平面上待插值点的色差。

5) 确定待估计的像素分量。

3.1 插值平面：估计点的分量和点的分量

1) 估计点的分量。

第1步：预测点的色差值。

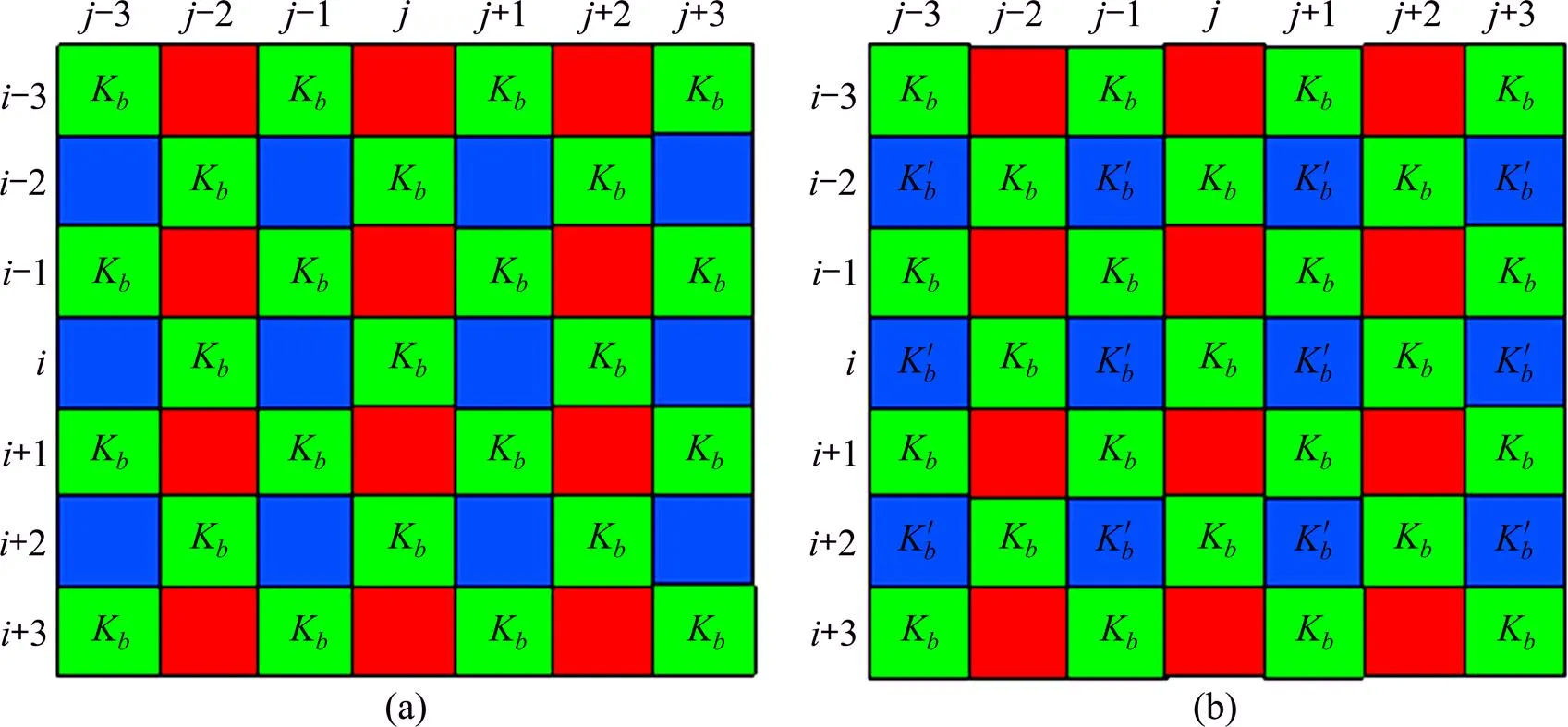
①构造色差平面r。在点利用(其中在偶数行)和(其中在奇数行)构造色差平面r，如图2(a)。

(a) 在G点，利用G分量和与之相邻的R分量构造的色差平面；(b) 估计出(a)平面上R点的色差值后的色差平面(为R点的估计值)

②构建原始样本集。在色差平面K上，以每一个K为中心点，若其周围5×5区域内K均存在，则以该点的K作为输出样本构造2个样本模式。

模式1：利用图1(a)中M所在位置的K构造7维输入样本，处的K为输出样本。

模式2：以图1(a)中所在位置的K构造7维输入样本，处的K为输出样本。

③训练成员回归机。按照bagging-rough SVM集成算法的步骤1~5进行。

④构造测试样本并预测点处的K色差。此步为bagging-rough SVM集成算法的步骤6。

在图2(a)上，以每一个点为中心点，在其周围的3×3区域内构造测试样本，估计该中心点的K。例如，若上、下、左、右的4个K存在，则以，，，，|−|，|−|，(+++)/4作为上一步训练好的成员回归机的输入，成员回归机就可以预测出处的K。最后将各成员回归机预测的结果采用均值法融合输出，其输出即为点的。图2(b)所示为预测出所有点的色差的示意图。

第2步：计算出点的分量。利用公式计算出点的分量，其中为第1步预测出的点处的色差。例如，利用可得点的分量。

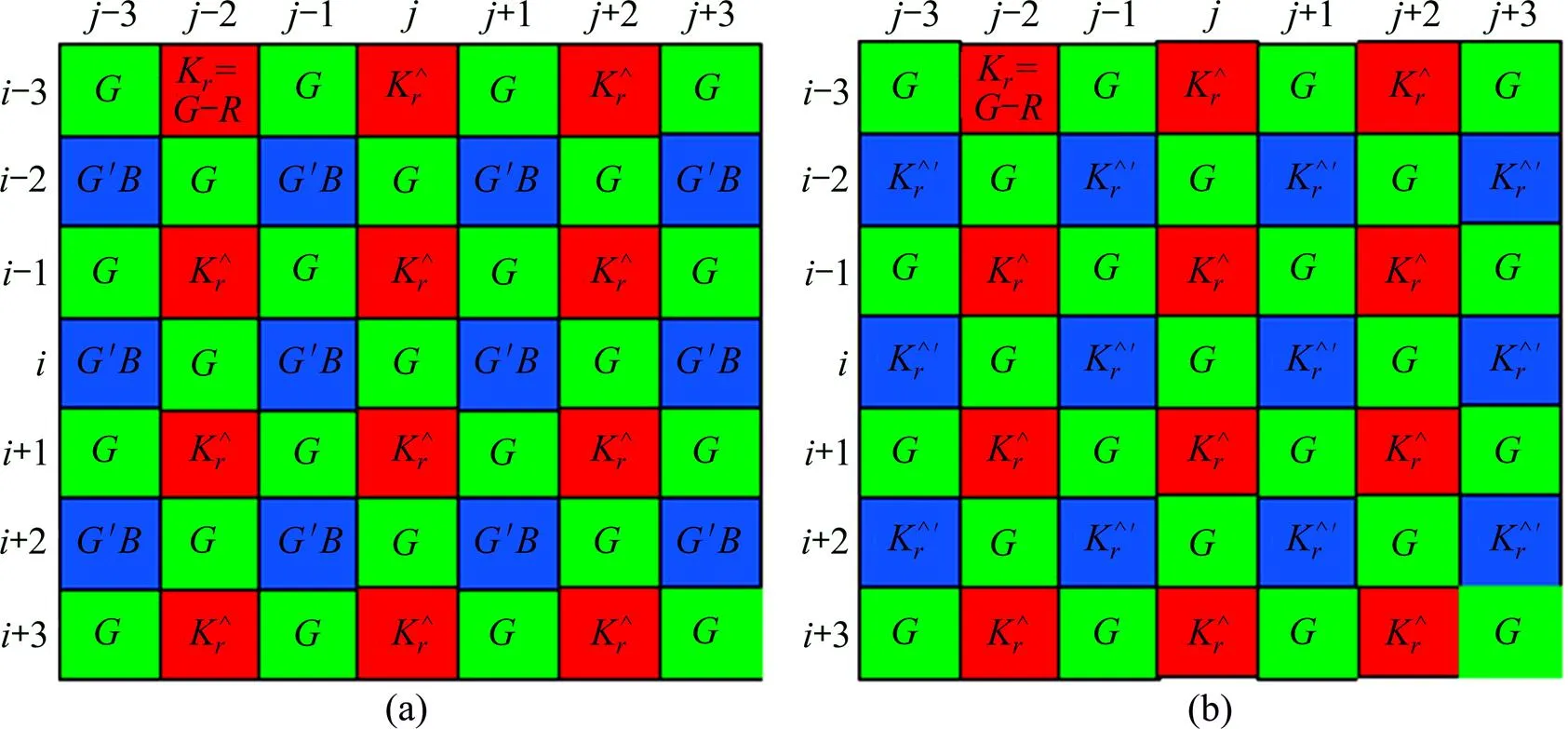
2) 估计点的分量。与本节1)的步骤类似，不同之处是在图3(a)的K色差平面上进行，K色差平面利用公式(在偶数行)和(在奇数行)构造；然后按照(1)中的方法预测所有点的色差得到图3(b)(为估计值)；最后利用点估计出的色差及公式计算出所有点的分量，

(a) 在G点，利用G分量和与之相邻的B分量构造的色差平面；(b) 估计出(a)平面上B点的色差后的色差平面(为B点的估计值)

此时，平面上的所有分量均为已知，可在插值和平面时使用。

3.2 插值平面：估计点的分量和点的分量

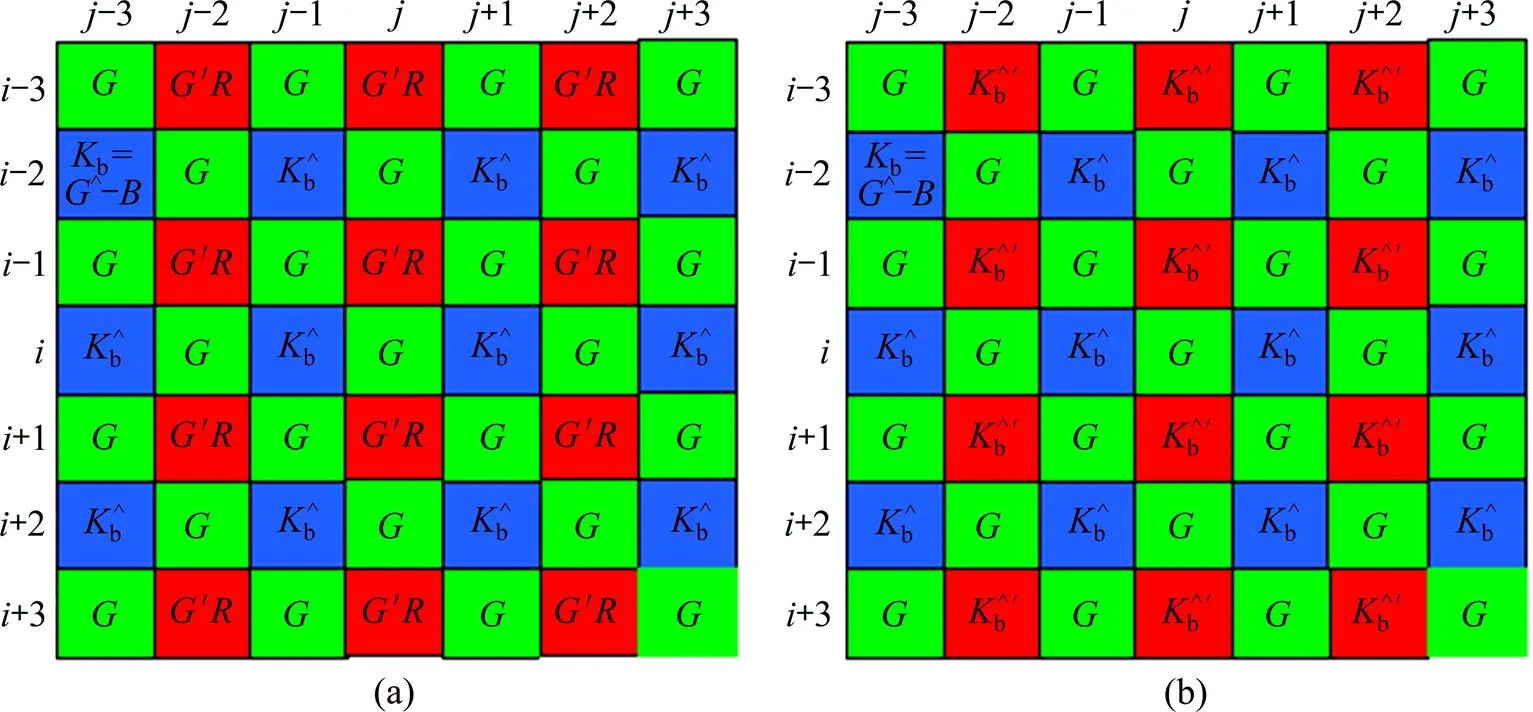
在马赛克图像的点利用该点的分量及插值平面时估计的′分量构造图4(a)的色差平面，此步在每个点利用实现。

(a) 在R点，利用插值G平面时估计的G′分量及该点的R分量构造的色差平面；(b) 估计出图4(a)平面上B点的色差后的色差平面(为B点的估计值)

1) 估计点的分量。

第1步：预测点处的色差。

模式1：利用图1(b)中所在位置的K值构造7维输入样本，处的K为输出样本。

模式2：以图1(b)中N所在位置的K构造7维输入样本，处的K为输出样本。

②训练成员回归机。按照bagging-rough SVM集成算法的步骤1~5进行。

在图4(a)上，以每一个点为中心点，在其周围的3×3区域内构造测试样本，估计该中心点的。例如，若4个邻角的色差存在，则以，，，，|−|，|−|，(+++)/4作为上一步训练好的成员回归机的输入样本，即可预测出点的。最后将各成员回归机预测的结果采用均值法融合输出，其输出即为点的值。图4(b)所示为预测出所有点的的示意图。

第2步：计算点的分量。利用公式计算点的分量，其中为第1步估计出的点处的色差。例如，利用可得点的分量。

2) 估计点的分量。在图4(b)上，以每一个点为中心点，在其周围的3×3区域内构造测试样本，估计该中心点的。例如，若上、下、左、右的色差均存在，则以，，，，|−|，|−|，(+++)/4作为输入样本，用估计点的分量时训练好的成员回归机即可预测出点的色差值；然后将各成员回归机预测的结果采用均值法融合输出，其输出即为点的；最后利用计算出点的分量，其中是估计出的点的色差。

3.3 插值平面：估计点的分量和点的分量

在马赛克图像的点利用该点的分量及插值G平面时估计的分量构造图5(a)的色差平面，此步在每个点利用实现。

1) 估计点的分量。此步和插值平面时的(1)类似，不同之处在于其插值过程在图5(a)的色差平面上实现：先在平面上构建原始样本集，再利用粗糙集约简算法约简的样本训练成员回归机；然后用训练好的成员回归机预测点的色差。图5(b)所示为预测出所有点色差的示意图(为估计值)。最后利用公式计算点的分量。

2) 估计点的分量。此步骤与插值平面的步骤2)类似，在图5(b)上，利用估计点的分量时训练好的成员回归机预测点的色差，然后利用公式计算出点的分量。

(a) 在B点，利用插值G平面时估计的G′分量及该点的B分量构造的色差平面；(b) 估计出图5(a)平面上R点的色差后的色差平面(为R点的估计值)

4 仿真实验及结果分析

采用Lin等开发的SVM软件工具箱(LIBSVM)在MATLABR2009b中仿真，选择-SVR作为成员回归机，成员回归机使用径向基函数RBF，其余参数采用默认设置。为了说明本文方法的有效性，对被广泛作为测试图像的柯达彩色图像进行测试，先获取彩色图像的Bayer型马赛克图像，然后利用文献[2−3，5−7，9]中的方法与本文的方法进行去马赛克，再利用客观评价指标彩色图像峰值信噪比(CPSNR)和S-CIELAB空间的色差，及主观评价方法对去马赛克的效果进行 评价。

CPSNR是基于RGB颜色空间恒量两幅彩色图像在矢量模上的误差，其值越大表明图像的插值效果越好，其计算公式为

S-CIELAB系统融合了人类的空间视觉特征，将半色调网点过滤成人眼响应的模糊模式，可以对整副图像进行点对点的色差计算，色差越小说明图像的失真越小，其色差计算公式为

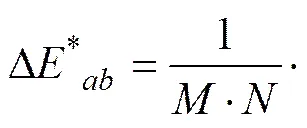
表1给出了对24幅标准彩色图像进行测试所得的客观指标CPSNR和，加粗的数字表示最优指标。从表1可以看出：文献[3]和[5]中的去马赛克方法获得的2项指标均不理想，其去马赛克的效果劣于其他方法；文献[2，6，9]中的方法均获得了较高的CPSNR，但较大，说明结果图像存在严重失真；文献[7]的方法获得了较小的，失真较小，接近本文方法所得结果，但CPSNR低于本文方法0.64 dB；本文方法获得了最高的CPSNR和最小的，表明其结果图像的质量优于其他方法，本文获得了最好的去马赛克效果。

表1 不同方法的客观指标rCPSNR及的比较

Table 1 rCPSNR and comparison of different demosaicing approaches

表1 不同方法的客观指标rCPSNR及的比较

编号文献[2]中方法文献[3]中方法文献[5]中方法文献[6]中方法文献[7]中方法文献[9]中方法本文方法 rCPSNRrCPSNRrCPSNRrCPSNRrCPSNRrCPSNRrCPSNR 139.371.3337.992.0335.922.6140.012.9139.951.2640.391.2340.471.20 240.711.5440.491.5039.701.6340.232.1339.291.5741.411.4840.231.35 343.190.8742.641.0041.001.1642.490.9142.300.9041.130.9543.130.88 441.291.1840.511.5139.641.6540.311.2240.001.2141.881.1841.611.01 538.701.9238.041.9836.152.5638.152.6538.011.9437.471.9738.291.90 640.051.0138.101.7436.942.0340.630.9940.790.9841.060.9941.170.98 742.831.0342.731.1341.031.3841.521.9641.631.1241.641.2042.891.00 836.421.4635.202.4533.343.1636.742.9237.611.4337.971.4138.021.37 943.280.8042.581.2140.731.4142.301.9842.970.7741.850.8543.400.77 1042.700.8242.521.1941.131.3942.431.9742.330.7942.560.7942.920.78 1140.221.2639.461.5638.091.8340.562.4640.581.2541.011.2341.041.21 1243.530.6642.631.1041.131.2743.641.3543.510.6343.940.6444.050.63 1335.292.0934.382.9033.643.2736.423.1136.292.0635.102.1436.562.03 1437.951.6537.131.8735.522.2036.472.7736.321.7235.801.7538.231.45 1540.211.3639.491.4339.091.5640.151.8539.231.3840.441.3440.451.32 1643.620.8941.161.3740.141.5344.310.9244.360.8244.420.8844.510.85 1742.011.3341.361.2740.441.3942.281.7442.121.3041.501.4742.621.31 1837.472.2037.732.0537.012.2337.762.9237.172.2836.962.4337.402.25 1941.271.1540.131.5737.391.8841.351.9241.361.1341.411.1441.461.13 2041.001.1841.331.2340.091.3941.271.9340.950.9540.931.2041.290.97 2139.741.2038.961.7037.621.9539.872.5239.921.1540.211.1540.271.14 2238.871.4238.281.8937.082.0938.512.4038.361.4438.311.6238.881.36 2342.411.1742.911.1341.621.2242.500.9541.451.0442.221.2442.400.91 2435.631.3934.821.9034.282.2235.462.4235.121.4035.421.4935.631.31 Avg40.321.2939.611.6138.281.8840.222.0440.071.2740.211.3240.711.21

图6所示为利用本文方法对柯达彩色图像进行测试的部分结果图像及其放大区域。由图6可见：结果图像中基本不存在虚假色，尤其是容易出现虚假色或者锯齿现象的含有边缘较多的区域获得了理想的结果图像，有效保存了图像的细小边缘区域的边缘特征。图7所示为对柯达19采用不同去马赛克方法获得的结果图像的局部放大区域。从图7可看出：文献[3]和文献[5]中的方法获得的结果图像中虚假色非常明显；文献[2]中方法去马赛克的效果优于文献[3]和[5]的方法，结果图像中的虚假色明显减少；文献[6]和文献[9]的结果图像中基本没用虚假色，但栅栏边缘较模糊，视觉效果不理想；文献[7]的结果图像中栅栏的边缘信息保存的较好，但有少许的虚假色；本文方法消除了虚假色、且保存了栅栏边缘的信息，获得了最好的去马赛克效果。图中的视觉效果和表1中的客观指标一致。

(a) kodak14；(b) kodak14的放大区域；(c) kodak15；(d) kodak15的放大区域；(e) kodak17；(f) kodak17的放大区域；(g) kodak20；(h) kodak20的放大区域

(a) 标准图像；(b) 本文方法；(c) 文献[2]的方法；(d) 文献[3]的方法；(e) 文献[5]的方法；(f) 文献[6]的方法；(g) 文献[7]的方法；(h) 文献[9]的方法

仿真实验的主客观指标表明，文中提出的SVM集成方法改善了图像的细小边缘区域的边缘特征，减少了结果图像中的伪彩色、锯齿现象，提高了成像 质量。

SVM训练过程实质是求解一个二次规划问题，假定原始样本集的规模为，子样本集的规模是(＜)，每个样本的维数为，SVM训练算法的时间复杂度为(SV3)，内存空间为(SV2)。本文算法的时间复杂度最坏可以达到(SV3+SV2+SV)，其中( )为时间函数，SV为支持向量的个数。经过粗糙集约简后，样本维数降低，子样本集的差异性增加，算法的时间复杂度减小，能够显著提高成员SVM的精度及其成员之间的差异性。SVM集成把原始样本集分成若干子样本集，能够发挥SVM解决小样本问题的优势，保证了算法具有较好的泛化能力。因此，本文算法能保证SVM集成的精度及图像插值效率。

5 结论

1) 采用bootstrap技术重取样原始样本集，利用粗糙集动态约简重取样出的样本特征，能够保证训练样本的差异性，有利于构建差异性大、精度高的成员回归机，有效提高成员回归机的预测精度。

2) 在基于色彩相关性及色差恒定原理构建的色差平面上构造原始样本集，利用bagging-rough算法估计色差平面上的待插值点的色差值，进而计算出彩色图像上丢失的颜色分量的方法，能获得较好的去马赛克效果。

3) 据所提方法获得的结果图像具有较好的客观指标及良好的视觉效果，能有效保存图像的细小边缘区域的边缘特征。

[1] Lukac R, Plataniotis K N. Color filter arrays: design and performance analysis[J]. IEEE Trans on Consum Electron, 2005, 51(4): 1260−1267.

[2] Mairal J, Elad M, Sapiro G. Sparse representation for color image restoration[J]. IEEE Trans on Image Processing, 2008, 17(1): 53−69.

[3] CHANG Lanlan, TAN Y P. Effective use of spatial and spectral correlations for color filter array demosaicking[J]. IEEE Trans on Consumer Electronics, 2004, 50(1): 355−365.

[4] Moghadam A A, Aghagolzadeh M, Kumar M, et al. Compressive framework for demosaicing of natural images[J]. IEEE Trans on Image Processing, 2013, 22(6): 2356−2371.

[5] Lukac R, Plataniotis K N. Data-adaptive filters for demosaicking: A framework[J]. IEEE Trans on Consum. Electron, 2005, 51(2): 560−570.

[6] Ferradans S, Bertalmio M, Caselles V. Geometry-based demosaicking[J]. IEEE Trans on Image Processing, 2009, 18(3): 665−670.

[7] CHUNG Kuoliang, YANG Weijen, YAN Wenming, et al. Demosaicing of color filter array captured images using gradient edge detection masks and adaptive heterogeneity-projection[J]. IEEE Trans on Image Processing, 2008, 17(12): 2356−2367.

[8] CHUNG Kuoliang, YANG Weijen, CHEN Pangyen, et al. New joint demosaicing and zooming algorithm for color filter array[J]. IEEE Trans on Consumer Electronics, 2009, 55(3): 1477−1486.

[9] HAO Pengwei, LI Yan, LIN Zhouchen, et al. A geometric method for optimal design of color filter arrays[J]. IEEE Trans Image Process, 2011, 20(3): 709−722.

[10] 贾晓芬, 马立勇, 马家辰. 基于支持向量机的彩色滤波阵列插值方法[J]. 四川大学学报(工程科学版), 2010, 42(3): 145−150. JIA Xiaofen, MA Liyong, MA Jiachen. Support vector machines based color filter array interpolation scheme[J]. Journal of Sichuan University: Engineering Science Edition, 2010, 42(3): 145−150.

[11] Pekkucuksen I, Altunbasak Y. Edge strength filter based color filter array interpolation[J]. IEEE Trans on Image Processing, 2012, 21(1): 393−397.

[12] Vapnik V N. The nature of statistical learning theory[M]. New York: Springer, 1995:20−50.

[13] HUANG Xin, ZHANG Liangpei. An SVM ensemble approach combining spectral, structural, and semantic features for the classification of high-resolution remotely sensed imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(1): 257−272.

[14] Saha I, Maulik U, Bandyopadhyay S, et al. SVMeFC: SVM ensemble fuzzy clustering for satellite image segmentation[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(1): 52−55.

[15] Dietterich T G. Machine learning research: Four current directions[J]. AI Magazine, 1997, 18(4): 97−136.

[16] Dietterich T G. An experimental comparison of three methods for constructing ensembles of decision trees Bagging boosting and randomization[J]. Machine Learning, 2000, 40(2): 139−158.

[17] Breiman L. Bagging predictors[J]. Machine Learning, 1996, 24(2): 123−140.

[18] Schapire R E. The strength of weak learn ability[J]. Machine Learning, 1990, 5(2): 197−227.

[19] Robert B, Ricardo G O, Francis Q. Attribute bagging: improving accuracy of classifier ensembles by using random feature subsets[J]. Pattern Recognition, 2003, 36(6): 1291−1302.

[20] Pawlak Z. Rough sets[J]. International Journal of Computer and Information Science, 1982, 11: 341−356.

[21] HE Qiang, XIE Zongxia, HU Qinghua, et al. Neighborhood based sample and feature selection for SVM classification learning[J]. Neurocomputing, 2011, 74(10): 1585−1594.

[22] WANG Tinghua, HUA Jialin, LI Xiangjun, et al. Rough set-based feature weighting to improve SVM classification[J]. Journal of Computational Information Systems, 2012, 8(8): 3359−3367.

[23] 张寒波, 黄辉先, 王耀南. 基于粗糙集约筒的特征选择神经网络集成技术[J]. 控制与决策, 2010, 25(3): 37l−387. ZHANG Hanbo, HUANG Huixian, WANG Yaonan. Feature selection neural network ensemble based on rough sets reducts[J]. Control and Decision, 2010, 25(3): 37l−377.

(编辑 陈爱华)

Demosaicing based on bagging rough-set support vector machine ensemble

JIA Xiaofen, ZHAO Baiting, ZHOU Mengran, CHEN Zhaoquan, HUANG Xianbo

(College of Electrical & Information Engineering, Anhui University of Science and Technology, Huainan 232001, China)

A support vector machine (SVM) ensemble based demosaicing algorithm was proposed, which can reduce edge artifacts and false color artifacts effectively, and improve the image edge feature. Firstly, original sample set was constructed by applying inter-pixel correlation on green-red or green-blue color difference plane. The color difference plane was constructed by applying inter-channel correlation of the R, G, B channels and the constant color difference principle. Secondly, the training samples were selected by using the conventional bagging algorithm was used to re-sample the original sample set, and use the rough set reduction algorithm to dynamically reduce sample characteristics of the re-sampled samples. Thirdly, the individual support vector regression (SVR) was trained with the reduced training samples, and forecast the unknown color difference between two color channels (green-red or green-blue was forecast). Finally, the missing color value at each interpolated pixel was calculated using the forecasted color difference. Simulation results show that the proposed approach produces visually pleasing full-color result images and obtains higherCPSNRand smaller colour differenceof S-CIELAB than other conventional demosaicing algorithms.

demosaicing; support vector machine; ensemble; rough set

10.11817/j.issn.1672-7207.2015.06.013

TN919.3

A

1672−7207(2015)06−2065−09

2014−06−15；

2014−08−09

国家自然科学基金资助项目(51174258，11105002)；安徽高校省级自然科学研究项目(KJ2013B087)；淮南市科技计划项目(2013A4017)；大学生创新创业训练计划项目(201310361205)(Projects (51174258, 11105002) supported by the National Natural Science Foundation of China; Project (KJ2013B087) supported by Anhui Provincial Natural Science Research Projects in Central Universities, China; Projects (2013A4017) support by the Guidance Science and Technology Plan Projects of Huainan, China; Project (201310361205) supported by the Youth Foundation of Anhui Universityof Science & technology of China)

赵佰亭，博士，副教授，从事图像处理和智能控制等研究；电话：0554-6631012；E-mail：zhaobaiting@126.com