基于dSPACE的新型双滑模PMSM控制方法

高雅，刘卫国，骆光照



基于dSPACE的新型双滑模PMSM控制方法

高雅，刘卫国，骆光照

(西北工业大学自动化学院，陕西西安，710072)

设计一种基于滑模理论的永磁同步电机控制系统，利用滑模控制器代替传统的PID控制器，用滑模观测器代替传统的位置传感器。滑模控制器中针对传统滑模控制的抖振问题，引入准滑模和趋近律的概念，设计一种新的滑模控制器。滑模观测器使用连续饱和函数代替传统的开关函数，有效地减少高频噪声信号，经李亚普诺夫稳定方程证明系统的稳定性。本设计方法充分发挥滑模控制的优势。通过dSPACE实验平台的验证和ControlDesk环境的实时观测，证明所设计的新的滑模控制器在消除抖振和抗干扰方面明显优于传统的滑模控制器和PID控制器，滑模观测器能准确地观测位置信号，而且针对具有噪声干扰的场合，加入卡尔曼滤波器，有效地减少了干扰信号。

永磁同步电机；滑模变结构；SVPWM；卡尔曼滤波器；硬件仿真；dSPACE

永磁同步电机(PMSM)具有结构简单、体积小、质量小、效率和功率因数高、转动惯量小等优点。但由于PMSM是一个多变量、强耦合、非线性、变参数的复杂对象。采用常规PID控制在高精度控制方面存在一定问题，如受参数和外界干扰影响比较大等。而现代控制理论为PMSM的控制如自适应控制、模糊控制[1]、神经网络控制、鲁棒控制[2]和滑模变结构控制等[2−8]起了很大促进作用。而滑模变结构由于对系统数学模型的精度要求不高，对系统参数变化、外界环境扰动以及内部摄动等具有完全的自适应性和很强的鲁棒性、并且算法简单，易于工程实现。在交流调速系统控制领域显示了良好的应用前景。在PMSM的控制中，实时、准确的位置信号的获得对于整个系统的性能有着重要的影响。通常，位置信号的检测是通过安装在电机轴上的光电编码器或霍尔器件等传感器。但硬件的存在带来很多问题，而且在一些特殊场合，硬件传感器的安装无法实现。因此，无位置传感器成为一个重要的研究课题。目前应用比较广泛的无位置传感器检测方法主要有：1) 利用电机的电磁关系或电流、电压与反电动势的关系等内在联系计算位置。但这种方法对电机参数特别敏感，而且转速较低时估算不准确。2) 基于感应电动势的观测器估计法。如卡尔曼滤波观测器和滑模观测器等[9−13]。卡尔曼滤波观测器算法复杂，需要矩阵求逆运算，计算量相当大，同时要用到许多随机误差的统计参数，需通过大量的调试才能确定合适的随机参数。滑模观测器对系统参数变化、外界环境扰动及内部摄动等具有完全的自适应性，对系统数学模型精度要求不高，动态响应快，具有较好的鲁棒性，易于工程实现，目前得到了广泛的应用。3) 基于凸极效应的高频电压或电流注入法[14]。该方法虽然可以应用于较宽的速度范围且低速时也可得到较好的估算结果，但由于存在多个滤波器，使得转子位置估算有时间滞后，从而导致动态性能变差, 而且高频信号的注入带来高频噪声问题和需要特殊的硬件支持。为此，本文作者设计一种基于滑模理论的永磁同步电机控制系统，利用滑模控制器代替PID控制器，用滑模观测器代替传统的位置传感器，并经李亚普诺夫稳定方程证明了系统的稳定性。设计方法充分发挥了滑模控制的优势。经实验验证，设计的滑模控制器的控制性能上明显优于传统的PID控制器，滑模观测器能准确的观测位置信号。而且针对具有噪声干扰的场合，加入了卡尔曼滤波器，有效减少了干扰信号。

1 基于卡尔曼滤波的滑模变结构控制

1.1 卡尔曼滤波原理

卡尔曼滤波器(KFC)是通过一种算法排除可能的随机干扰，是提高系统精度的一种手段。它是用状态方程和递推的方法根据上一状态的估计值和当前状态的观测值推出当前状态估计值的滤波方法，因而卡尔曼滤波对信号的平稳性和时不变性没有要求[15]。

卡尔曼滤波的过程包括预测过程和更新过程。预测过程包括式(1)计算状态估计值和式(2)计算误差协方差。

更新过程包括式(3)计算修正矩阵、式(4)更新观测值和式(5)更新误差协方差。

1.2 基于卡尔曼滤波的SVPWM滑模控制器设计

SVPWM(电压空间矢量脉宽调制)是利用三相逆变器所形成的8种开关状态去获得参考电压矢量所需要的理想圆形磁场。它的特点是可以简单地采用软件实现，输出电压的利用率高，开关次数恒定和不会引起谐波电流。

滑模变结构控制是一种不连续控制，即拥有一种使系统结构随时间变化的开关特性。而这种控制特性可以迫使系统在一定特性下沿规定的状态轨迹作小幅度、高频率的“滑模”运动。但系统需满足运动点到达切换面()=0附近时都是终止点这一要求，即稳定性要求，切换面()需满足条件。

滑模变结构控制器的设计包括切换函数s(x)的确定和控制函数的求解[16]。

根据滑模变结构原理，滑模可达性条件仅保证由状态空间任何位置运动点在有限时间内到达切换面的要求，而采用趋近律可以有效的改善趋近运行的动态品质。本文运用指数趋近律为，其中表示系统的运动点趋近切换面=0的速率，而指数趋近律中的指数项解为，从中可知，在趋近过程中，趋近速度逐渐的减小到零，缩短了趋近时间而且使到达切换面的速度很小，减少了抖动。但在指数趋近律中，由于存在开关信号，还是存在抖振现象，本文利用饱和函数sat()代替了符号函数sgn(s)。其中为“边界层”。

设有噪声干扰的速度控制器的状态方程和输出方程为：

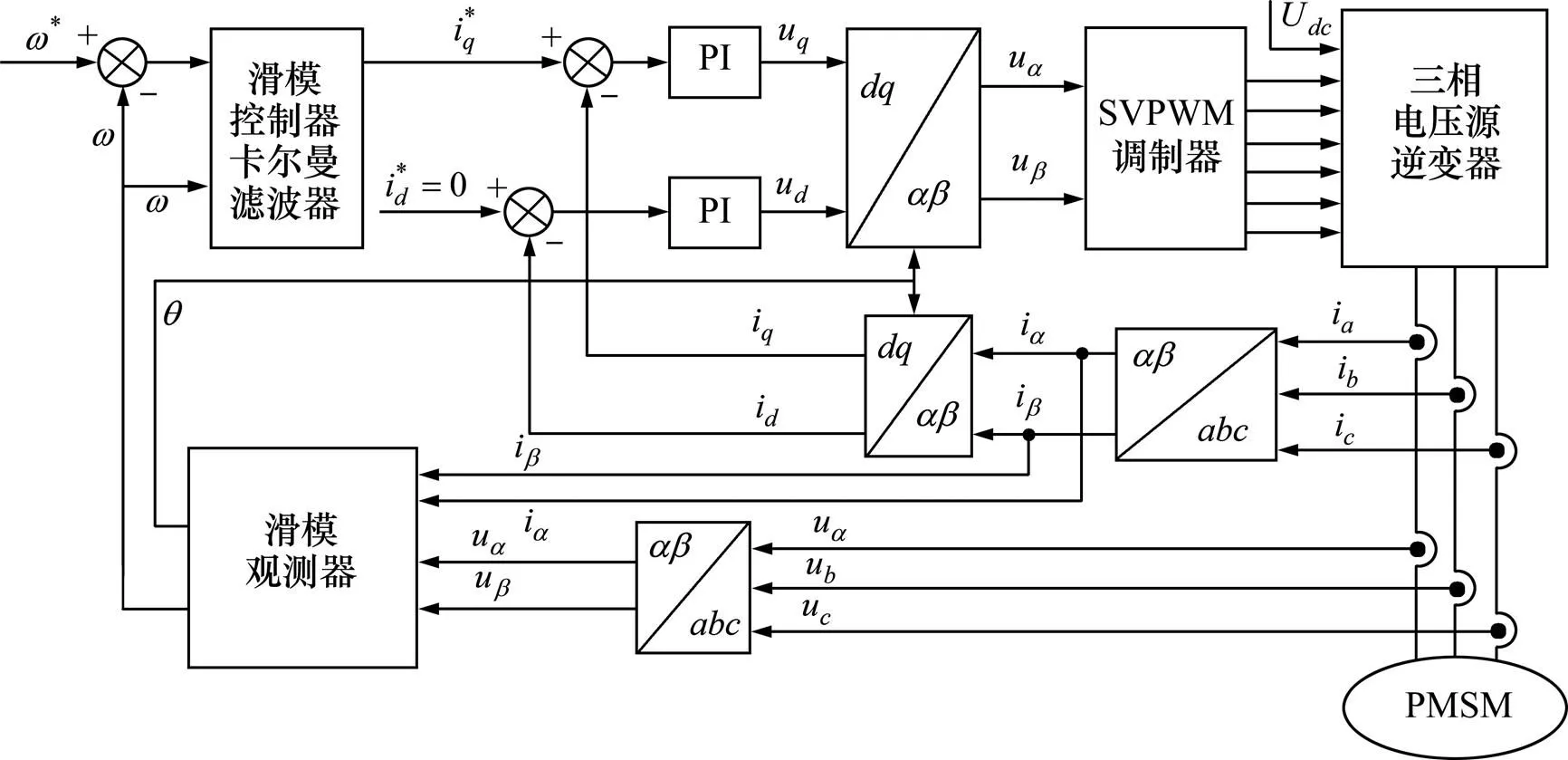
图1 基于卡尔曼滤波的PMSM双滑模控制结构框图

为了使系统满足稳定性要求，利用李雅普诺夫(Lyapunov)函数进行了系统的稳定性证明。根据李雅普诺夫函数的稳定性要求，设计的滑模控制器的稳定性条件需满足。

根据上面设计的滑模切换函数得

其中：＞0，＞0，可知结果值小于零，满足李雅普诺夫稳定性要求。

2 滑模位置观测器的设计

根据永磁同步电机的数学模型，结合SVPWM的调制方法，设计的基于滑模观测器的永磁同步电机矢量控制结构框图如图1所示，其中观测器的输入为坐标下的轴与轴的定子电流和定子电压。

2.1 滑模观测器的位置估计

永磁同步电机在两相静止坐标系下的数学模型为：

根据上面永磁同步电机的数学模型，建立以定子电流为状态变量的滑模观测器。其中表达式可表示为

式(17)可写成

定义动态误差:

由式(20)减去式(16)得

建立理想状态的滑模面：

由上面的式(23)和式(24)得

根据式(16)可知：中含有位置信息。而由于饱和函数(e)的存在，使通过式(25)计算的反电势存在一定的高频信号，需进行低通滤波。经过低通滤波的反电势方程为：

式中：0为低通滤波器的截止角频率。

由式(14)，(15)和(26)可得位置估计信号为

2.2 位置相位补偿

由于低通滤波器的存在，从而使上面计算的位置值与实际位置值存在一定的相位差。而在相同的截止频率和不同的转速下，对应不同的相位差，转速越大，相位差越大。于是本文将截止频率设置成1个与转速频率相关的变量，即

于是，将式(28)代入低通滤波器方程为

从上式可知，在不同的转速频率下，低通滤波器的相移不变，即

3 仿真和实验结果

本文首先利用Matlab对设计的基于SVPWM的带有卡尔曼滤波的滑模控制器和滑模观测器进行了仿真，对其有效性和准确性进行了验证，然后通过dSPACE(Digital signal processing and control engineering )实时实验平台，对设计的控制器和观测器进行实验验证。

dSPACE实验平台包括与Matlab/Simulink相连的软件接口，ControlDesk实时控制软件及一些与被控对象相连的外围硬件电路。图3所示为dSPACE实验平台的结构框图。

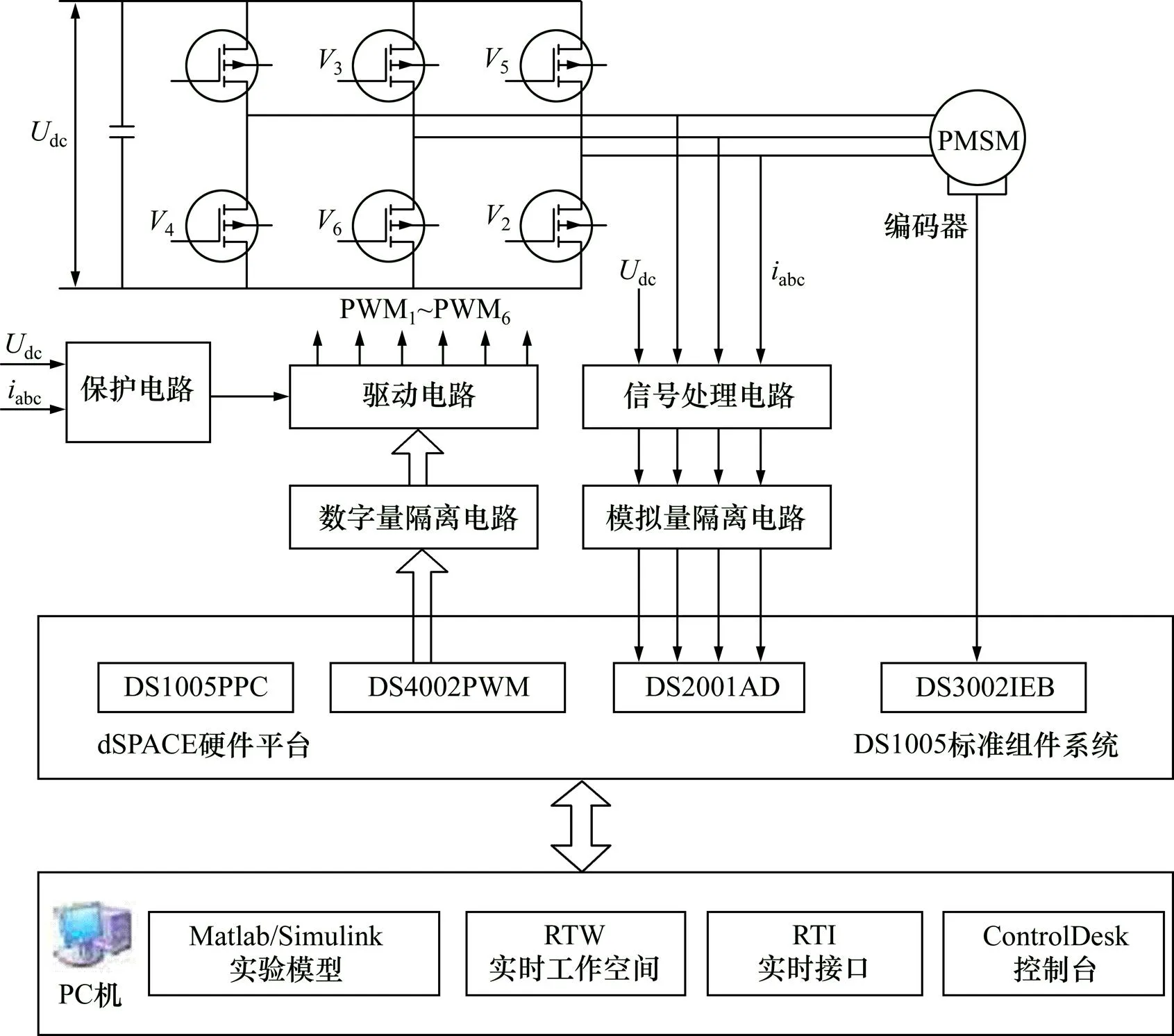
图3 dSPACE实验平台的结构框图

实验中的永磁同步电机的参数为：额定电压=160 V，额定转速=2 000 r/min，=4，s=1.7 Ω，d=q=0.012 8 H，=0.001 kg·m2，=0.002，f=0.148 8 Wb。

仿真时转速设置为700 r/min，负载设置为=0 s时L=1 N·m, 在=0.3s时L=2 N·m. 图4所示为3种不同控制方法下的转速波形。其中，从图4可以看到：传统的滑模控制抖振比较大，但当负载在0.3 s发生变化时，PID控制的速度曲线出现明显的瞬时抖动，而后面速度也存在滞后现象。由上可知：在负载发生变化时，滑模控制比PID控制的防抖动效果好，速度跟随性也强于PID控制。尤其是改进后的滑模控制，控制性能明显优于PID控制。

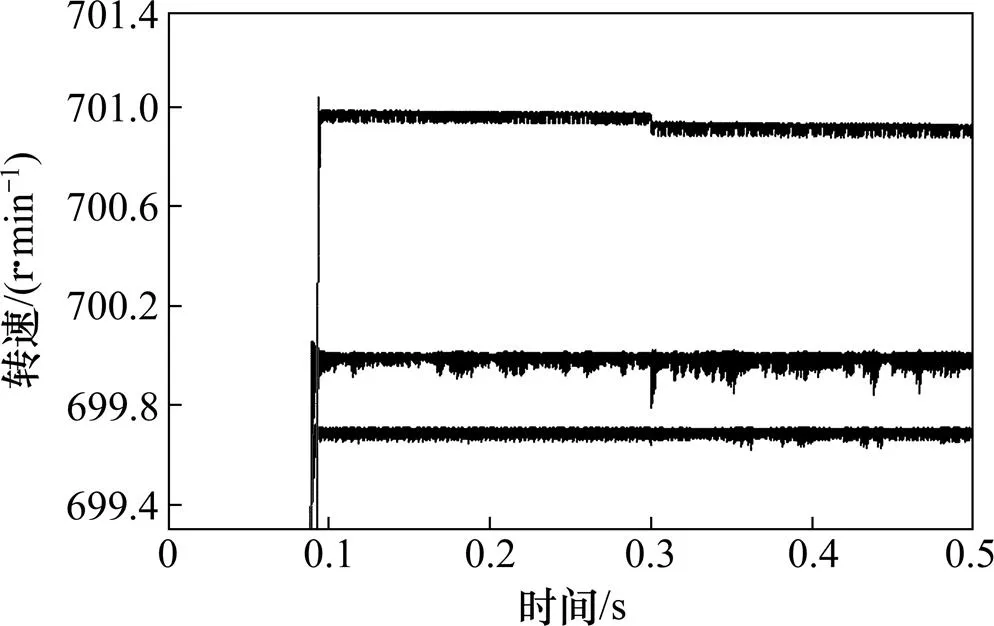
1—传统PID控制；2—传统滑模控制；3—本文改进后的滑模控制

对于具有噪声干扰场合的控制系统，本文加入了卡尔曼滤波器，对噪声干扰进行了滤除。设置噪声为[−1.2，1.2]内的白噪声信号，为[−0.3，0.3]内的白噪声信号，卡尔曼滤波算法中取=1，=1。图5(a)所示为加入噪声后未经滤波的转速曲线，曲线存在很大的干扰信号；图5(b)所示为经过卡尔曼滤波后的转速曲线，曲线比较平滑，没有夹杂噪声干扰信号，而且与图5(a)相比，它的跟随性明显好于图5(a)中曲线。

(a) 未经滤波的速度曲线；(b) 经过滤波的速度曲线

图6(a)所示为根据控制系统的数学模型积分得到的位置值与实际位置值的比较曲线；图6(b)所示为设计的滑模观测器观测的位置值与实际位置值的比较曲线，图6(c)和(d)分别为图6(a)和(b)实验开始时的曲线放大。从图6可以看出：设计的观测器更能准确的反应实际值，而且在开始启动时，滑模观测器的跟随性优于普通的积分器。

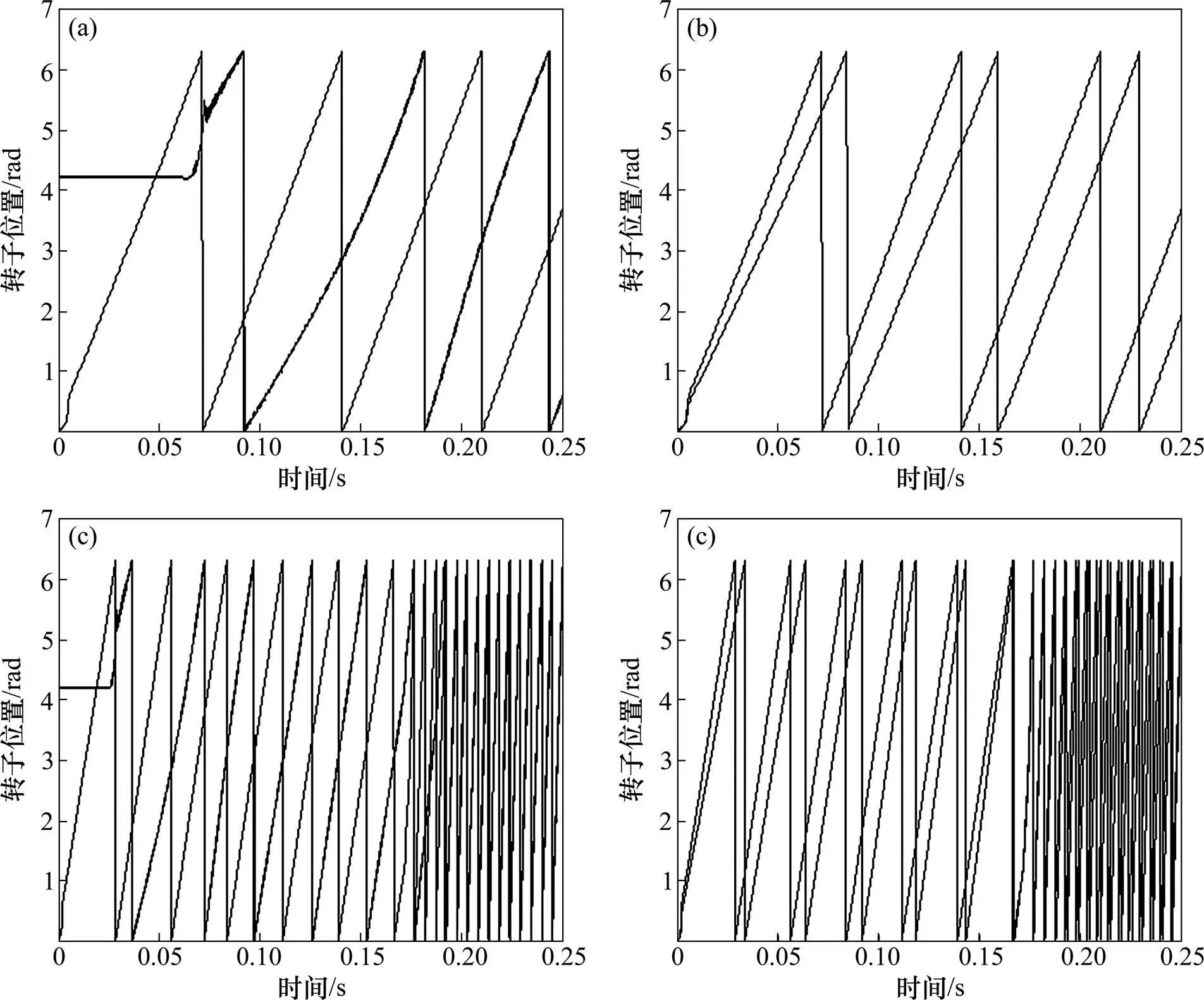
(a) 积分值与实际值的比较曲线；(b) 滑模观测器值与实际值的比较曲线；(c)实验开始时积分值与实际值的放大曲线；(d) 实验开始时滑模观测器值与实际值的放大曲线

在同样负载条件下，图7(a)所示为实验时用SPWM调制方法时的电流波形，图7(b)所示为采用SVPWM调制方法时的电流波形。从图7可以看出：利用SVPWM调制方法时，电流波形更接近于正弦，在同样条件下，电流更小，也就是说利用率更高，而利用SPWM调制方法时，电流畸变比较明显。而且在实验中发现利用SPWM调制方法时对电机初始位置估计的准确度要求明显比SVPWM调制方法的高。

(a)利用SPWM调制方法时的电流波形；(b)利用SVPWM调制方法时的电流波形

图8(a)所示为利用本文设计的滑模控制器控制时的转速波形，图8(b)所示为使用传统的PID控制时转速波形。从图8可以看到：本文设计的滑模控制器的控制性能明显优于传统的PID控制器，而且在实验中PID的参数调整存在很大的随机性，需要花费一定时间不断地进行校正。

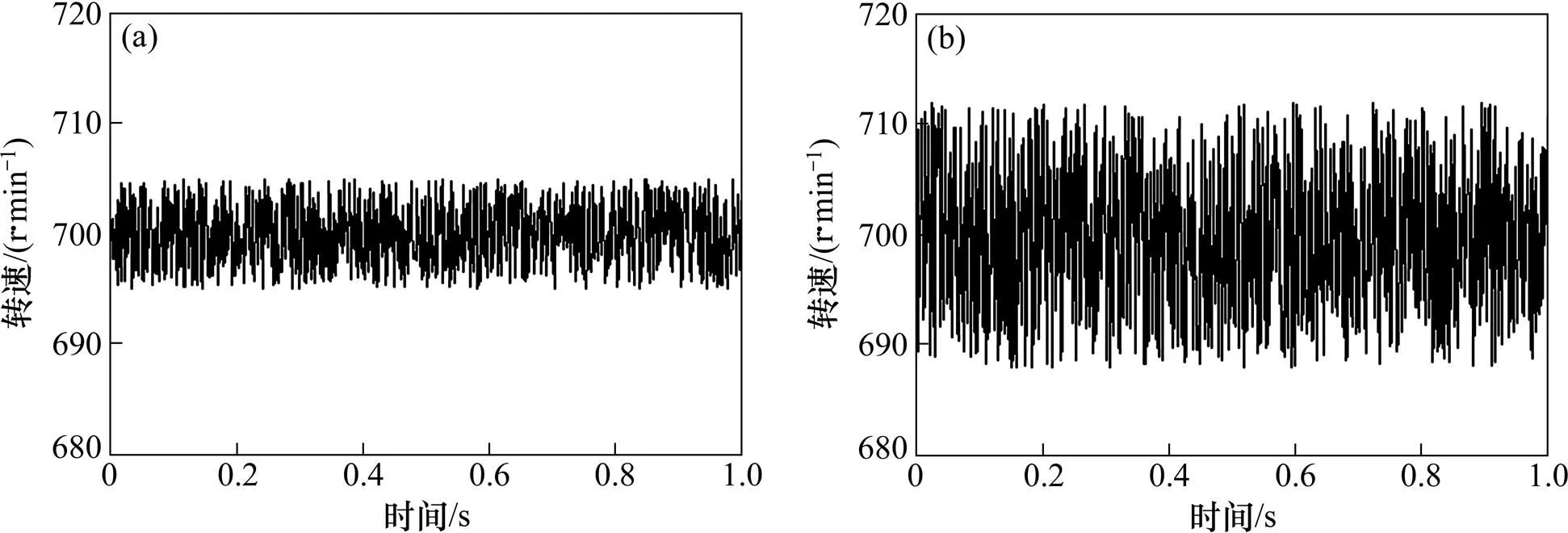
(a) 滑模控制器控制时的速度曲线；(b) PID控制器控制时的速度曲线

4 结论

1) 设计了一种基于滑模理论的永磁同步电机控制系统，即将滑模控制器和滑模观测器相结合，共同运用在永磁同步电机的控制系统中。

2) 使用滑模控制器代替了传统的PID控制器，并针对传统滑模控制存在抖振问题，在原有的基础上进行了一定改进。设计的滑模观测器使用连续饱和函数代替传统的开关函数，有效地减少了高频噪声信号。经李亚普诺夫稳定方程证明了系统的稳定性。

3) 本文设计方法充分发挥了滑模控制的优势。通过dSPACE实时实验平台的验证和在ControlDesk环境的实时观测，证明了所设计的新的滑模控制器在消除抖振和抗干扰方面明显优于传统的滑模控制器和PID控制器，滑模观测器能准确地观测位置信号，而且针对具有噪声干扰的场合，加入了卡尔曼滤波器，有效减少了干扰信号。

[1] SHEN Yanxia, WU Dinghui, JI Zhicheng. Model reference fuzzy adaptive control of permanent magnet synchronous motor[C]//Proceeding of the Chinese Control Conference, 2006: 1522−1527.

[2] Zadeh M H, Yazdian A, Mohamadian M. Robust position control in DC motor by fuzzy sliding mode control[J]. Power Electronics, Electrical Drives, Automation and Motion, 2006, 23(26): 1413−1418.

[3] 汪海波, 周波, 方斯琛. 永磁同步电机调速系统的滑模控制[J]. 电工技术学报, 2009, 24(9): 71−77.WANG Haibo, ZHOU Bo, FANG Sichen. A PMSM sliding mode control system based on exponential reaching law[J]. Transactions of China Electrotechnical Society, 2009, 24(9): 71−77.

[4] Lai C K, Kuo K S. A novel motor drive design for incremental motion system via sliding-mode control method[J]. IEEE Trans on Industrial Electronics, 2005, 52(2): 499−507.

[5] 张希, 陈宗祥, 潘俊民, 等. 永磁直线同步电机的固定边界层滑模控制[J]. 中国电机工程学报, 2006, 26(22): 115−121.ZHANG Xi, CHEN Zongxiang, PAN Junmin, et al. Fixed boundary layer sliding mode control of permanent magnet linear synchronous motor[J]. Proceedings of the CSEE, 2006, 26(22): 115−121.

[6] Bandal V, Bandyopadhyay B, Kulkarni A M. Design of power system stabilizer using power rate reaching law based sliding mode control technique[C]//The 7th International Power Engineering Conference, IPEC 2005. 2005: 923−928.

[7] DING Kun. Active power factor correction using sliding mode control with reaching law[C]//Second IEEE Conference on Industrial Electronics and Applications. 2007: 1165−1167.

[8] 方斯琛, 周波, 黄佳佳, 等. 滑模控制永磁同步电动机调速系统[J]. 电工技术学报, 2008, 23(8): 29−35.FANG Sichen, ZHOU Bo, HUANG Jiajia, et al. Sliding mode control for PMSM drive system[J]. Transactions of China Electrotechnical Society, 2008, 23(8): 29−35.

[9] Albert Q, WU Bin. Sensorless control of permanent magnet synchronous motor using extended Kalman filter[C]//Canadian Conference on Electrical and Computer. 2004: 1557−1562.

[10] Bolognani S, Tubiana L, Zigliotto M. Extended Kalman filter tuning in sensorless PMSM drives[J]. IEEE Transactions on Industry Applications, 2003, 39(6): 1741−1747.

[11] Francesco. Sensorless speed control of a PMSM based on sliding mode observer and extended kalman filter[C]//IEEE Industry Application Conference IAS. 2001: 533−540.

[12] Kang K L, et al. Sensorless control of PMSM in high speed range with iterative sliding mode observer[C]//IEEE Applied Power Electronics Conference and Exposition APEC. 2004: 1111−1116.

[13] Batzel T D, Lee K Y. Electric propulsion with sensorless permanent magnet synchronous motor: implementation and performance[J]. IEEE Trans on Energy Conversion, 2005, 20(3): 575−583.

[14] 贾洪平, 贺益康. 基于高频注入法的永磁同步电动机转子初始位置检测研究[J]. 中国电机工程学报, 2005, 25(15): 15−20.JIA Hongping, HE Yikang. Study on inspection of the initial rotor position of a PMSM based on high-frequency signal injection[J]. Proceedings of the CSEE, 2005, 25(15): 15−20.

[15] 秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安: 西北工业大学出版社, 1998: 95−98. QING Yongyuan, ZHANG Hongyue, WANG Shuhua. Kalman filter and integrated navigation principle[M]. Xi’an: Northwestern Polytechnical University Press, 1998: 95−98.

[16] 刘金琨. 滑模变结构控制MATLAB仿真[M]. 北京: 清华大学出版社, 2005: 62−70. LIU Jinkun. Slinding mode variable structure control MATLAB Simulation[M]. Beijing: Tsinghua University Press, 2005: 62−70.

(编辑 陈爱华)

New dual-sliding mode control method of PMSM based on dSPACE

GAO Ya, LIU Weiguo, LUO Guangzhao

(College of Automation, Northwestern Polytechnic University, Xi’an 710072, China)

Based on the sliding mode theory, a new control system of permanent magnet synchronous motor was designed. It used a new sliding mode controller to replace the traditional one and PID one, and used the sliding mode observer to replace the position sensors. Aimed at the chattering question of conventional sliding mode controller, the concept of reaching law and quasi-sliding mode were introduced. In the designing processes of the sliding mode observer, using a continuous saturation function instead of the traditional switch function, high frequency noise signal was reduced. By dSPACE platform experimenting and ControlDesk real-time observing, the results show that the new sliding mode controller has a better effect for eliminating the chattering and the noise disturbed signal, and the position signal can be accurately observed by the sliding mode observer. Furthermore, Kalman filter controller is used in this control system for adapting to the noise disturbed area. According to the result, this design can decrease the noise signals effectively.

permanent magnet synchronous motor; sliding mode variable structure; space vector pulse width modulation (SVPWM); Kalman filter controller; hardware simulation; digital signal processing and control engineering (dSPACE)

10.11817/j.issn.1672-7207.2015.06.009

TM315

A

1672−7207(2015)06−2036−08

2014−06−12；

2014−08−13

国家自然科学基金资助项目(51177135)(Project (51177135) supported by the National Natural Science Foundation of China)

高雅，博士，从事电机与电器研究；E-mail：leave.999@163.com