水平荷载作用下煤矸石空心砖墙受力性能影响因素分析

卢林枫，张亚平



水平荷载作用下煤矸石空心砖墙受力性能影响因素分析

卢林枫1，张亚平2

(1. 长安大学建筑工程学院，陕西西安，710061；2. 广东华方工程设计有限公司四川分公司四川成都，610084)

在已有煤矸石空心砖墙抗震试验的基础上，利用ANSYS软件，建立试验有限元模型，并与试验结果进行对比分析，验证有限元模型的正确性。在试验有限元模型正确的前提下，结合工程实例，确定模型尺寸，同时考虑竖向压力、砂浆强度等级、洞口尺寸及位置变化等参数对水平荷载作用下煤矸石空心砖墙体受力性能的影响，设计3个系列23个试件，对每个试件在单调荷载和低周反复荷载作用下的受力性能进行有限元模拟分析。研究结果表明：竖向压力是影响空心砖墙体的主要因素，墙体的承载能力随竖向压力的增加而提高，墙体的延性及破坏形式则随竖向压应力与墙体平均抗压承载力的比值不同而表现出不同的形式；砂浆强度等级提高，墙体的承载能力随之提高，但延性减小；洞口大小及位置也是影响墙体受力性能的主要因素。墙体的极限承载力、延性和刚度随洞口尺寸的增大而减小；当洞口居中布置时，墙体的承载能力最小，而延性较好；当门洞靠边布置时，墙体的承载能力提高，延性减小。

煤矸石空心砖墙；极限承载力；延性系数；滞回性能

在国家强制淘汰和禁用黏土砖、发展环保型住宅体系的政策指导下，由工业固体废弃物煤矸石生产的空心砖被推广应用[1−2]。目前在煤矿区，煤矸石多孔砖是黏土实心砖的主要替代材料，在已成的建筑中得到广泛应用，例如在双鸭山市当地8层以下混合结构住宅90%以上采用了煤矸石多孔砖[3]。我国是一个多地震国家，大量的村镇住宅还是采用砌体结构，而煤矸石多孔砖可能是被广泛使用的空心砖种类之一，因此，研究煤矸石空心砖墙体的抗震性能，从保证砌体房屋安全使用上显得尤为重要。早期研究发现多孔砖墙体的抗压和抗剪强度及抗震性能都较实心砖墙体要 好[4−6]；随后，田春艳等[7]对1个足尺组合砌体模型进行了拟动力试验研究；梁建国等[8]对6片KP1型页岩粉煤灰多孔砖墙进行了抗震试验研究；刘小勤等[9−11]对煤矸石页岩空心砖的基本力学性能进行了试验研究，并提出了相关的计算公式；李鹏[12]对煤矸石多孔砖墙体进行了低周反复荷载作用下的试验研究，探讨了墙体的破坏特征、承载能力、延性和刚度；赵成文等[13−16]对煤矸石空心砖的基本力学性能及墙片抗震性能进行了较系统的试验研究。目前煤矸石空心砖墙体的基本力学性能研究已较成熟，但对水平荷载作用下煤矸石空心砖墙受力性能的试验和理论研究尚处于初步阶段，为进一步研究煤矸石空心砖墙体在水平荷载作用下受力性能的影响因素，本文作者在已有试验研究基础上，对煤矸石空心砖墙体进行变参数数值模拟分析，探讨有关因素对墙体受力性能的影响。

1 有限元模拟试验

1.1 原始试验资料

以文献[14]中的W-MFPJ-1试件为对象对煤矸石空心砖墙体抗震性能进行有限元模拟试验。W-MFPJ-1试件的水平配筋率为0.07%，长×宽×高为 1 600 mm×2 000 mm×240 mm，墙顶设置高为200 mm、强度等级为C20的混凝土压梁，墙体砌筑在高为350 mm、强度等级为C30的混凝土地梁上面，竖向压力为0.6 MPa，模拟6层房屋的底层墙片。试验加载以荷载控制分级施加，每级增加20 kN，当墙体开裂后，采用手动加载，当试验荷载下降到极限荷载的80%时，试验结束。

1.2 有限元分析模型

采用ANSYSY10.0有限元软件建立有限元分析模型，选用SOLID65单元模拟墙体，不考虑混凝土单元的压碎，张开裂缝和闭合裂缝剪力传递系数按文献[17]中建议值取值，分别取剪力传递系数为0.3和1.0。采用LINK8单元模拟墙体中的钢筋，钢筋与墙体的锚固连接采用共用节点方式来处理，并采用映射网格划分的方法对模型进行网格划分。煤矸石空心砖墙的材料本构关系见文献[18]提出的式(1)和式(2)。式中，为应力，为应变m为砌体抗压强度，0为相应于m的应变，u为极限压应变，墙体抗压强度平均值按试验取值，取0=0.003，u/0=1.6[18]。砌体材料的泊松比=0.20，弹性模量W=4213 MPa，空心砖墙采用多线性随动强化模型及Willam−Warnker五参数失效准则。钢筋采用双线性等向强化模型，屈服强度为275 MPa，钢材的泊松比=0.3，弹性模量S=21 000 MPa。

模型采用位移收敛准则，水平荷载推为“+”，拉为“−”，开裂前分别按cr/8，cr/4，cr/2和cr加载，每级循环1周，cr为砌体墙体的开裂位移；加载至开裂位移cr后，按cr/2递增控制加载，每级也循环1周，当结构承载力下降到最大荷载的80%时，停止加载。压力则以面力方式直接加在墙体顶部，并对墙体顶部所有节点进行方向位移耦合，水平荷载施加在主结点上，同时对墙体顶部施加方向约束，墙体底部为理想刚接。

1.3 有限元模拟试验的验证

在低周反复荷载作用下，W-MFPJ-1试件的承载力及变形能力对比情况如表1所示。从表1可看出：ANSYS计算值与试验值的误差在合理的范围之内，结果表明ANSYS有限元模拟与试验吻合较好，选用的单元形式、加载方式等具有一定的可行性和可靠性，能够较准确地反映试验试件的承载力、位移和破坏特征等信息。

表1 W-MFPJ-1试件承载力和变形能力对比分析

2 影响因素分析

结合工程实际，确定有限元分析试件的尺寸，同时考虑竖向压力、砂浆强度、洞口尺寸及位置变化等参数变化对煤矸石空心砖墙体受力性能的影响，设计3个系列23个试件，对每个试件在单调荷载和低周反复荷载作用下的受力性能进行模拟试验分析。

2.1 竖向压力的影响

2.1.1 YL试件的设计

改变墙体的竖向压应力，考察竖向压力对墙体受力性能的影响。墙体竖向压力分别按σ=0.03，0.06，0.09，0.12，0.15，0.21，0.27和0.33m取值(m为墙体平均抗压承载力)，取m=6.62 MPa，即分别等于0.2，0.4，0.6，0.8，1.0，1.4，1.8和2.2 MPa，共设计8个试件，对应试样编号为YL-1~YL-8。试件长×宽×高为3 600 mm×3 300 mm×240 mm，水平配筋率为0.11%，煤矸石空心砖墙体的砂浆及块材按文献[14]选取，材料本构关系按1.2节取值。

2.1.2 YL试件在单调荷载作用下的非线性分析

YL系列试件在单调荷载作用下的荷载—位移曲线如图1所示，试件的开裂位移cr、开裂荷载cr、极限位移u、极限荷载u以及延性系数u/cr和开裂强度系数u/cr随竖向压应力变化的曲线关系如图2所示。

试样：1—YL-1；2—YL-2；3—YL-3；4—YL-4；5—YL-5；6—YL-6；7—YL-7；8—YL-8

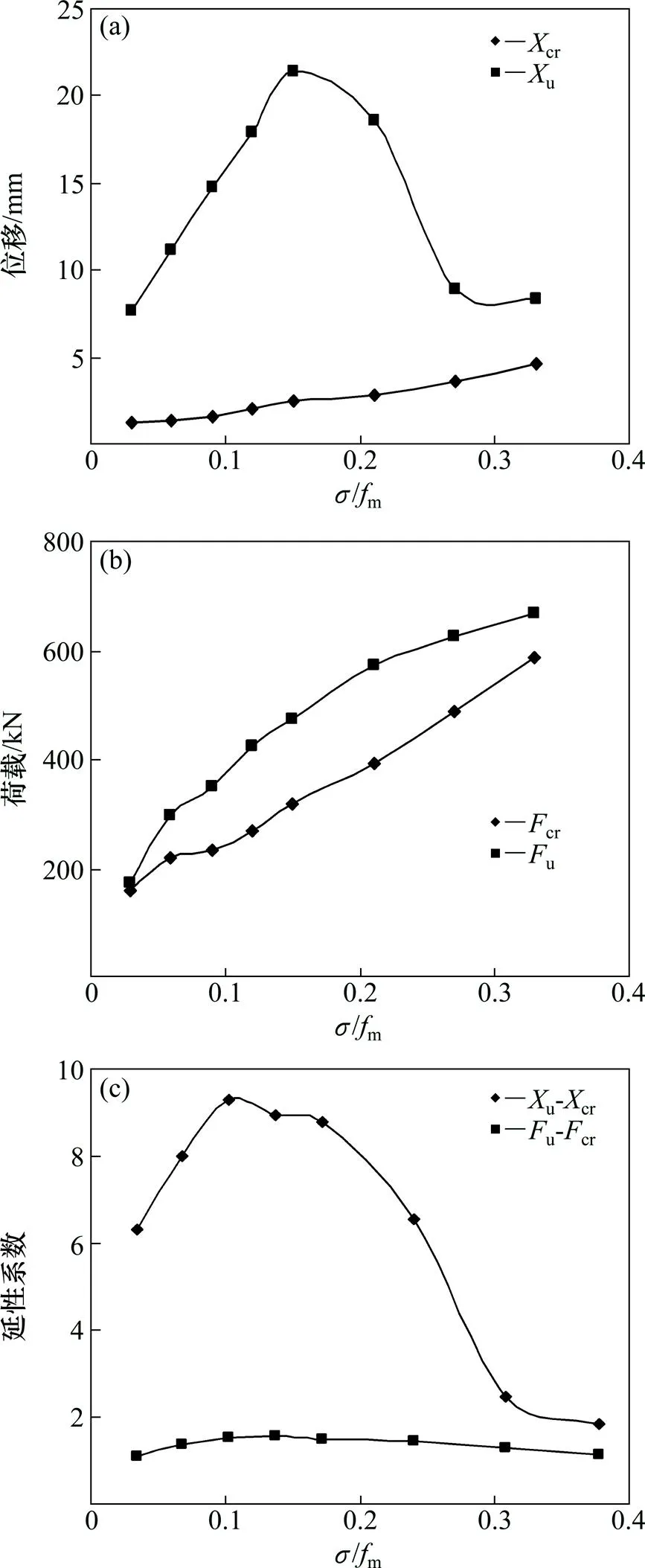
(a) 开裂和极限位移曲线；(b) 开裂和极限荷载曲线；(c) 延性系数曲线

从图1可看出：YL系列试件的荷载位移曲线在初始阶段基本在一条直线上，随着荷载的加大，极限荷载随的增大而增加。当≤0.15m时，极限荷载的增加速度较快，当≥0.21m时，极限荷载的增长速度较缓慢，表明当增加到一定程度时，不能大幅度提高墙体承载力。

从图2可知：YL试件的开裂位移、开裂荷载、极限荷载都随增大而增加；当0≤≤0.15m时，极限位移随增大而增加，当≥0.15m时，极限位移则迅速下降；延性系数较试验模型的大，这是因为有限元模拟的边界条件较理想、墙体材料未考虑初始缺陷等。从图2还可看出：当0≤≤0.12m时，延性系数随增大而提高，当≥0.12m时，延性系数则随增大而减小，最后趋于平缓；开裂强度系数则变化不大，表明竖向压力对墙体的开裂强度影响甚小。

2.1.3 YL试件在低周反复荷载作用下的非线性分析

YL系列试件在低周反复荷载作用下的滞回曲线如图3所示，骨架曲线如图4所示，割线刚度退化曲线如图5所示。

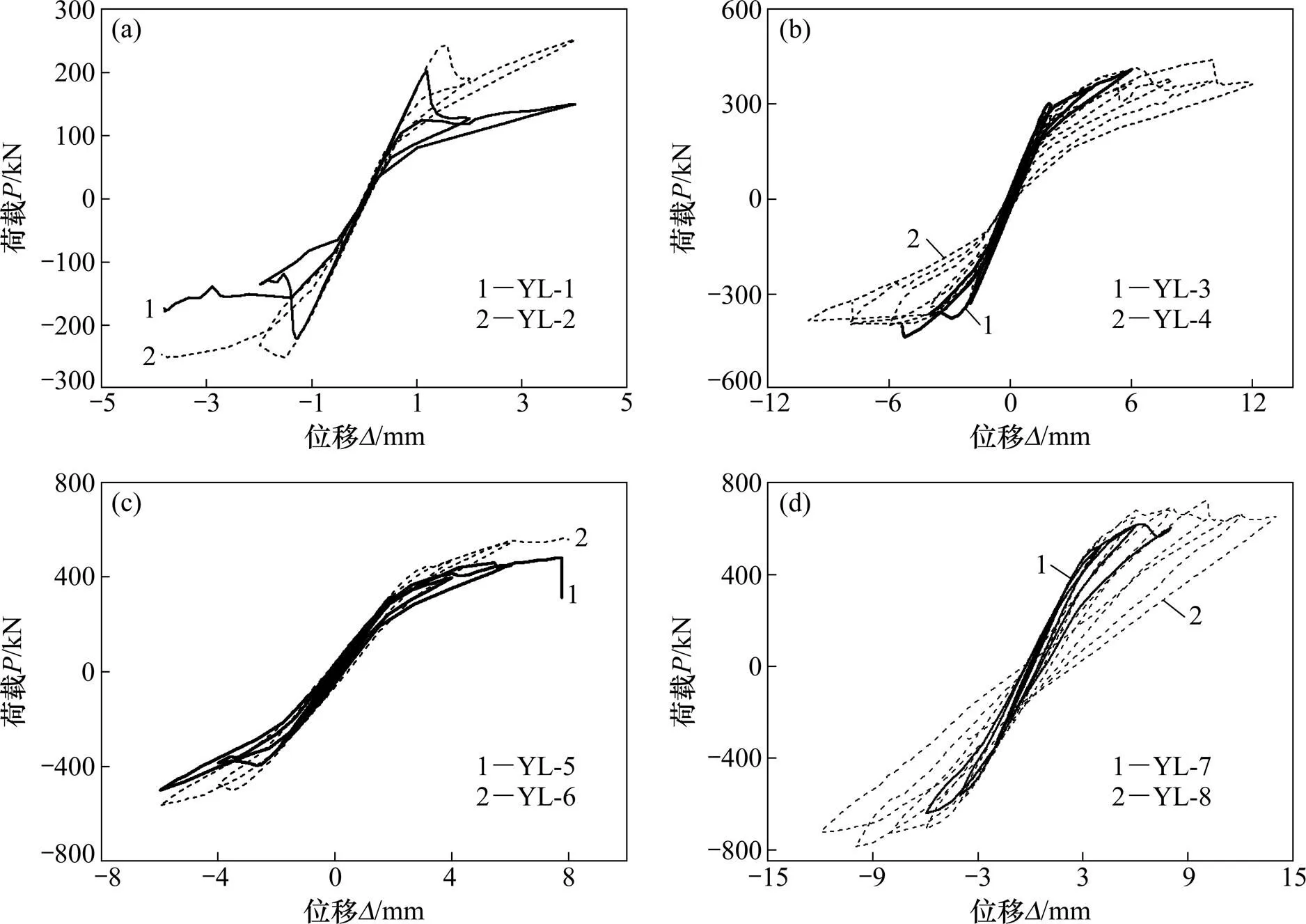
试样：(a) YL-1和YL-2；(b) YL-3和YL-4；(c) YL-5和YL-6；(d) YL-7和YL-8

试样：1—YL-1；2—YL-2；3—YL-3；4—YL-4；

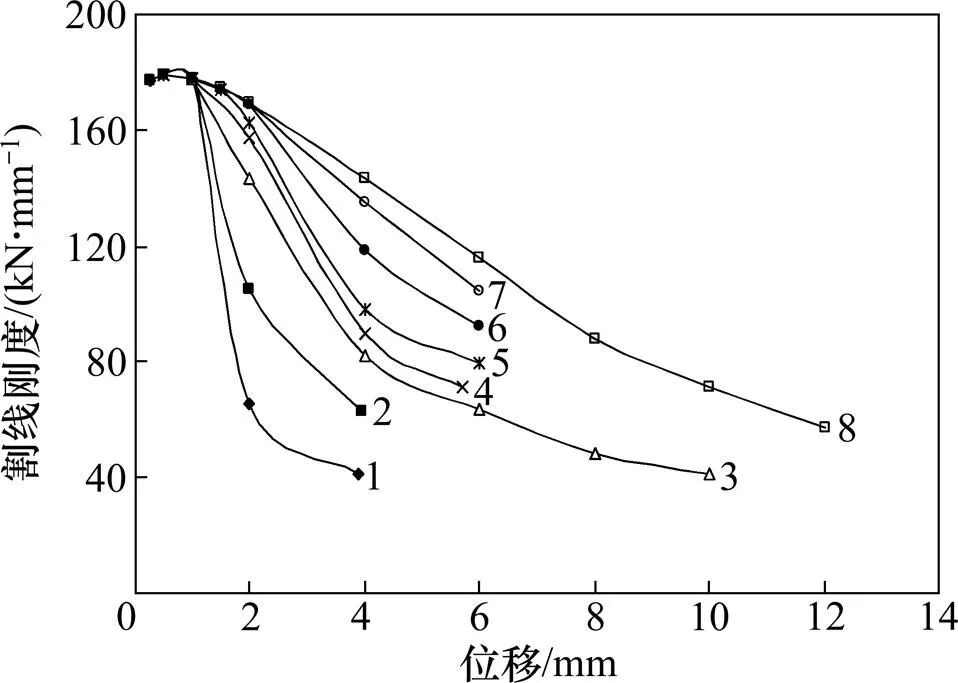
试样：1—YL-1；2—YL-2；3—YL-3；4—YL-4；

从图3可以看出：滞回曲线呈两头大中间颈缩的形状，这是因为有限元模型未能模拟墙体裂缝错动的产生。在/m＜0.21范围内，YL试件随竖向压力的增大，滞回环面积经历了从小到大又变小的变化，当/m＜0.09时(YL-3试件)，滞回曲线最饱满，破坏位移较大，破坏形式较理想，说明当/m=0.09左右时，墙体的抗震性能较好；之后随增大，墙体的抗震承载力逐渐加大，但延性减小，耗能能力减弱。当0.21≤/m≤0.33时，试件滞回环面积随的增大而增大，承载力及破坏位移也加大，如YL-8试件(即/m=0.33)，滞回曲线较饱满，破坏位移和极限承载能力较大。

文献[19]认为：当/m≤0.2时，墙体为剪切破坏，延性随竖向压力的增加而提高；当0.3≤/m≤0.7时，墙体破坏形式为剪压破坏；当/m≈0.5~0.6时，墙体抗侧承载力达到峰值，之后则下降；当/m≥0.7时，砌体破坏形式则为斜压破坏。

本文经分析也得出类似的结论。从图4可看出：试件的骨架曲线在低周反复加载时的变化趋势与单调加载时基本一致，在弹性阶段，对墙体承载力影响甚小；当墙体进入弹塑性阶段，墙体承载力随增加而增大，破坏位移则与墙体的破坏形式有关，当/m≤0.21时，YL-1~YL-6试件呈剪切破坏，在/m=0.09时，墙体的延性最好；当0.21≤/m≤0.33时，YL-7~YL-8试件为剪压破坏，墙体的破坏位移随的增大而增大。

从图5可知：YL试件的初始刚度基本相同，随着荷载的加大，刚度退化迅速，且随增加，刚度下降速度逐渐缓慢。这是因为增大，墙体裂缝发展缓慢，且随/m不同，裂缝由砂浆与块体的接触面向块体本身发展。

2.2 砂浆强度的影响

2.2.1 SJ试件的设计

SJ试件是改变墙体的砂浆强度等级，研究其对墙体受力性能的影响。SJ试件的煤矸石空心砖和砂浆强度等级依据GB 50003—2001“砌体结构设计规范”[20]规定取值，墙体的相关力学性能也按规范规定进行计算。试件长×宽×高为3 600 mm×3 300 mm×240 mm，水平配筋率为0.11%。试件的各个参数设置见表2。

表2 SJ系列试件相关设计参数

2.2.2 SJ试件在单调荷载作用下的非线性分析

SJ试件在单调荷载作用下的荷载−位移曲线如图6所示，试件相关力学性能随砂浆强度等级的变化曲线如图7所示。

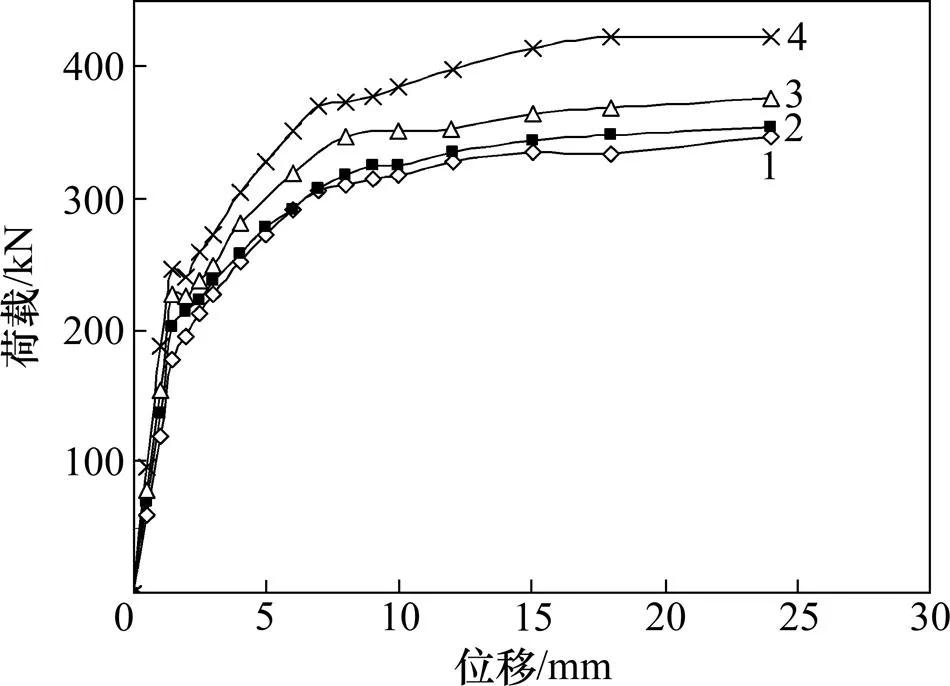
试样：1—SJ-1；2—SJ-2；3—SJ-3；4—SJ-4

(a) 开裂和极限位移曲线；(b) 开裂和极限荷载曲线；(c) 延性系数曲线

从图6可知：SJ试件的承载力随砂浆强度等级的增大而提高，砂浆等级相差幅度越大，极限荷载变化幅度也越大，但对墙体的位移影响甚小。

从图7可看出：随砂浆强度等级的增大，SJ试件的开裂位移和极限位移有所减小，但极限位移下降幅度较大；开裂荷载和极限荷载则随砂浆强度等级的增大而提高，但幅度不大，而延性系数随之减小。

2.2.3 SJ试件在低周反复荷载作用下的非线性分析

SJ系列试件在低周反复循环荷载作用下的滞回曲线如图8所示，骨架曲线如图9所示，割线刚度退化曲线如图10所示。

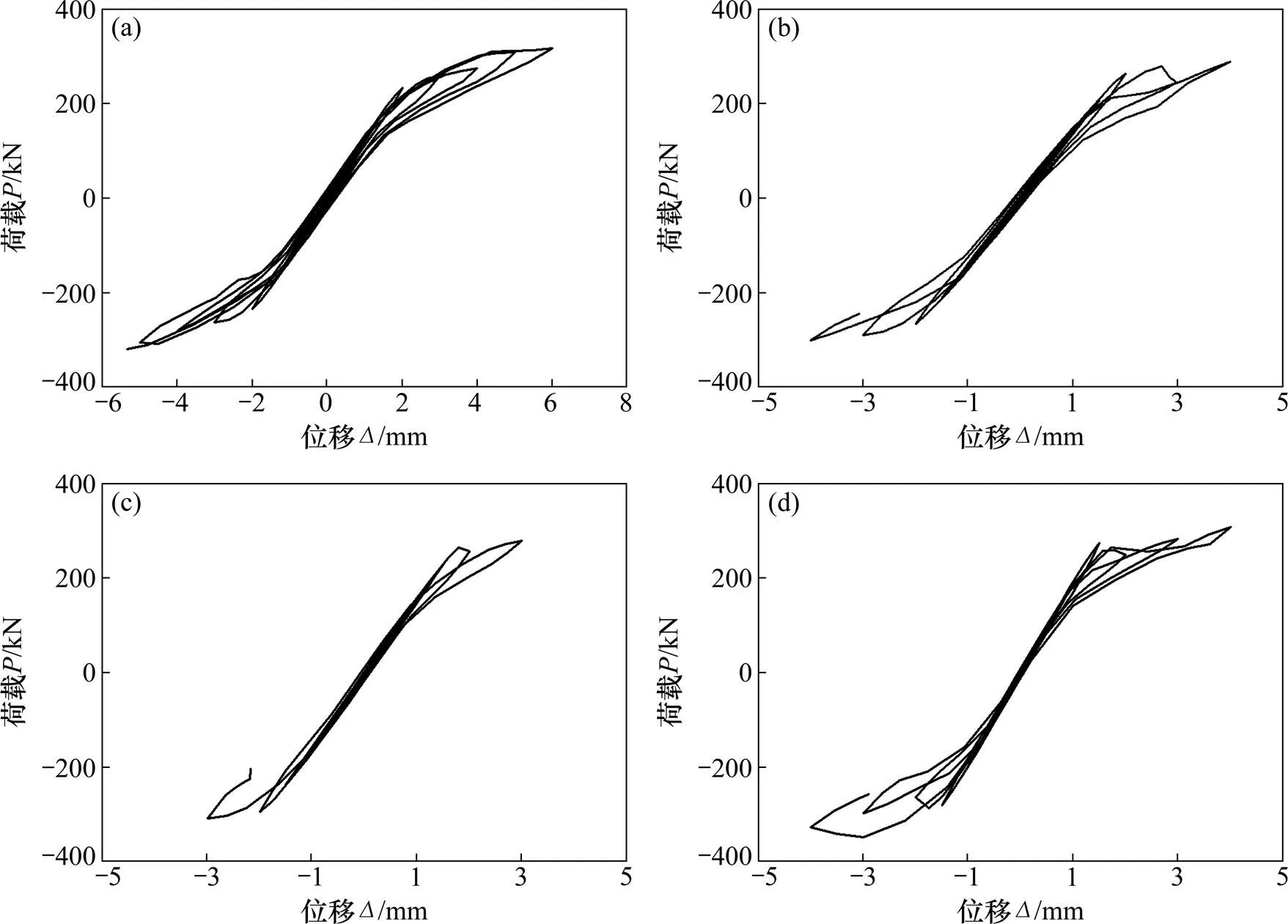
(a)SJ-1；(b) SJ-2；(c)SJ-3；(d) SJ-4

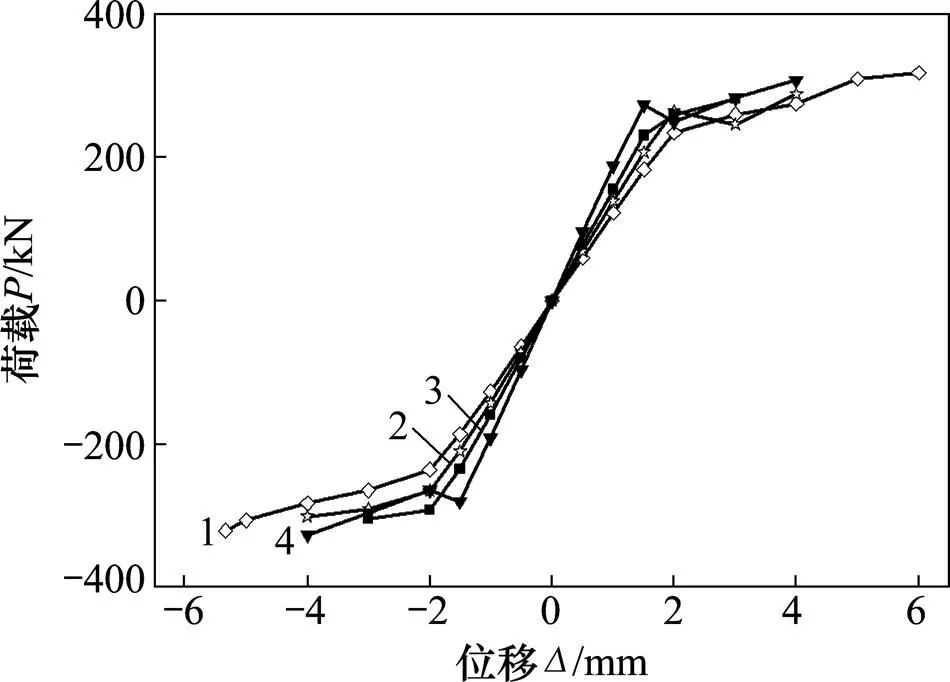
试样：1—SJ-1；2—SJ-2；3—SJ-3；4—SJ-4

试样：1—SJ-1；2—SJ-2；3—SJ-3；4—SJ-4

从图8可看出：SJ试件的滞回曲线随砂浆强度等级的提高逐渐呈捏缩状，所围面积和破坏位移减小，滞回性能减弱，脆性特征更明显。

从图9可知：砂浆强度等级越高，试件越快达到开裂荷载，此后快速达到极限状态，承载力提高，但位移减小。从图10可看出：试件的初始刚度随砂浆强度等级的提高而加大，开裂之前，刚度基本保持不变，出现裂缝后，刚度迅速下降，砂浆强度等级越高，刚度下降速度越快，最后趋于平缓。

综上分析可知：墙体的承载能力和初始刚度随砂浆强度等级的增大而提高，延性随之而降低，耗能能力减弱。

2.3 洞口尺寸及位置的影响

2.3.1 DK试件的设计

根据实际工程中门洞位置及尺寸，建立不同形式的开洞试件。墙体的砂浆及块材按文献[14]选取，材料本构关系按1.2节取值；对照模型PJ-1试件无门洞；同时假定门洞过梁的材性与墙体相同，共同受力；DK系列试件的长×宽×高为3 600 mm×3 300 mm×240 mm，无水平钢筋，相关参数设置如表3所示。

表3 DK试件相关设计参数

2.3.2 试件在单调荷载作用下的非线性分析

1) 门洞位置影响。PJ-1和DK-1~DK-3试件的荷载−位移曲线如图11所示，试件的相关力学性能随门洞位置变化的曲线关系如图12所示。

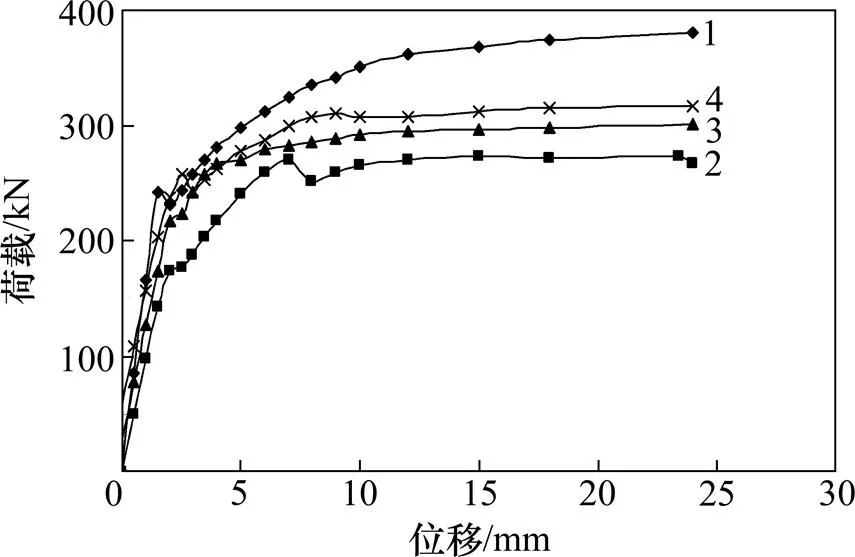
试样：1—PJ-1；2—DK-1；3—DK-2；4—DK-3

(a) 开裂和极限位移曲线；(b) 开裂和极限荷载曲线；(c) 延性系数曲线

从图11可知：开洞墙体的极限抗剪承载力远比无洞墙体的小，门洞居中布置时，极限承载力最小，是因为墙体主要靠对角线范围区域受力，门洞居中时对墙体对角线削弱程度最大；DK-2和DK-3在荷载为 0 N处出现负向水平位移，DK-3试件的负向位移较大，是由于门洞位置离墙边越近，墙肢高厚比越小，在竖向压力作用下，墙体发生压弯作用，产生负向位移，这也是门洞位置离墙边越近，墙体承载力越高的原因之一。

从图12可知：开洞墙体的开裂位移要比无洞墙体大，门洞居中布置时，开裂位移较小；开洞时，墙体的极限位移随门洞离墙边距离的增大而增大；开洞墙体的cr，u和延性较无洞墙体减小，门洞位置离墙边距离越远，cr和u就越小，而当门洞居中布置时，墙体的延性较好；墙体的开裂强度系数变化幅度不大。

2) 门洞尺寸影响。PJ-1，DK-1，DK-4和DK-5试件在单调荷载作用下的荷载−位移曲线如图13所示，试件的相关力学性能随门洞开洞率的变化曲线如图14所示。

1—PJ-1；2—DK-1；3—DK-2；4—DK-3

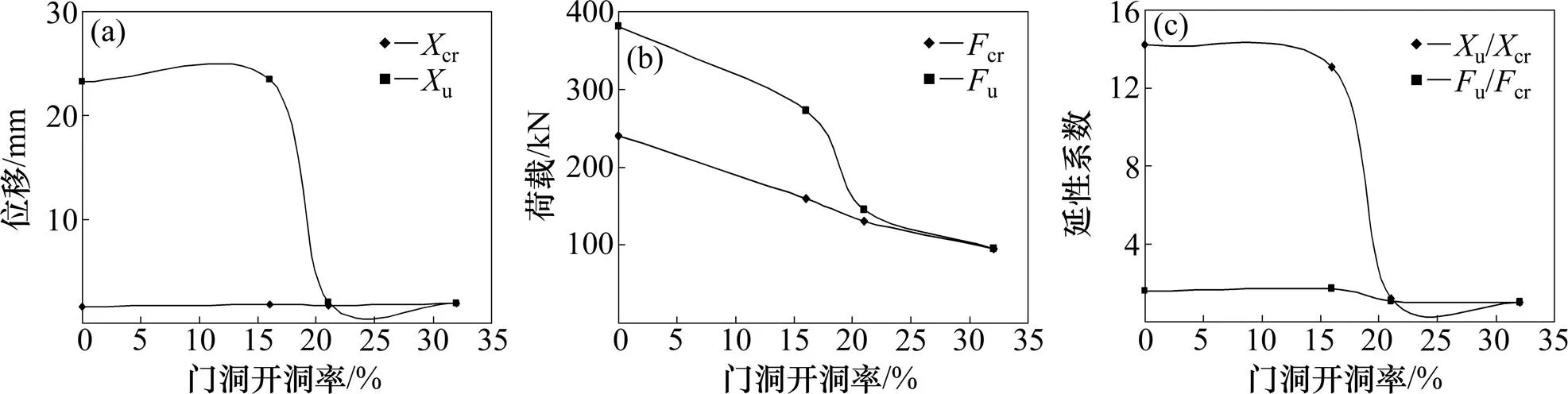
(a) 开裂和极限位移曲线；(b) 开裂和极限荷载曲线；(c) 延性系数曲线

从图13可知：墙体的极限承载力随门洞尺寸的增大而迅速减小，下降幅度很大；DK-4和DK-5试件还未进入弹塑性阶段，墙体已经破坏，是因为门洞尺寸的加大，一方面削弱了墙体底部约束，另一方面削弱了墙体对角线区域刚度，墙体刚开始开裂，裂缝就贯通墙体，失去承载能力。

从图14可看出：墙体的开裂位移随门洞开洞率的增大而略有增加，极限位移则随门洞尺寸的增大而迅速下降，PJ-1试件的极限位移约为DK-5试件的12倍，说明当门洞开洞率大于30%时，墙体基本失去抗侧能力。墙体的开裂荷载、极限荷载和延性随门洞尺寸的加大而下降；开裂强度系数变化不大。

2.3.3 试件在低周反复荷载作用下的非线性分析

PJ-1和DK系列试件在低周反复荷载作用下的滞回曲线如图15所示，骨架曲线如图16所示，刚度退化曲线见图17。

试样：(a) PJ-1；(b) DK-1；(c) DK-2；(d) DK-3；(e) DK-4；(f) DK-5

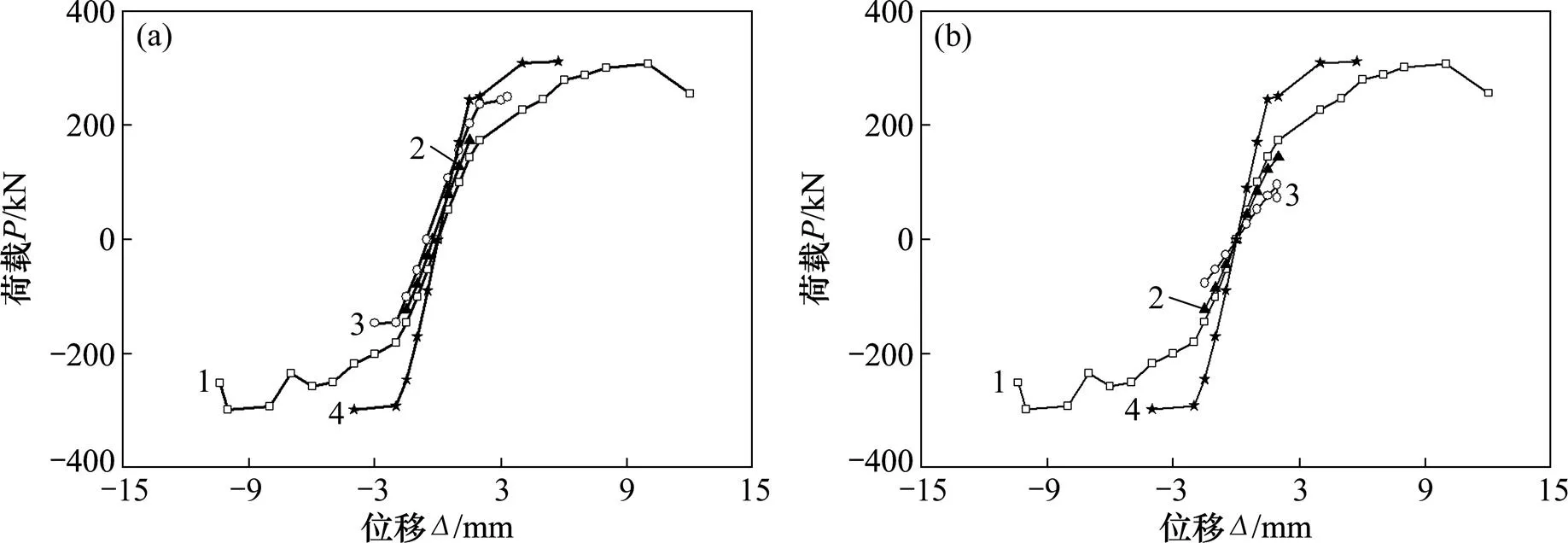
(a) 门洞位置变化；(b) 门洞尺寸变化

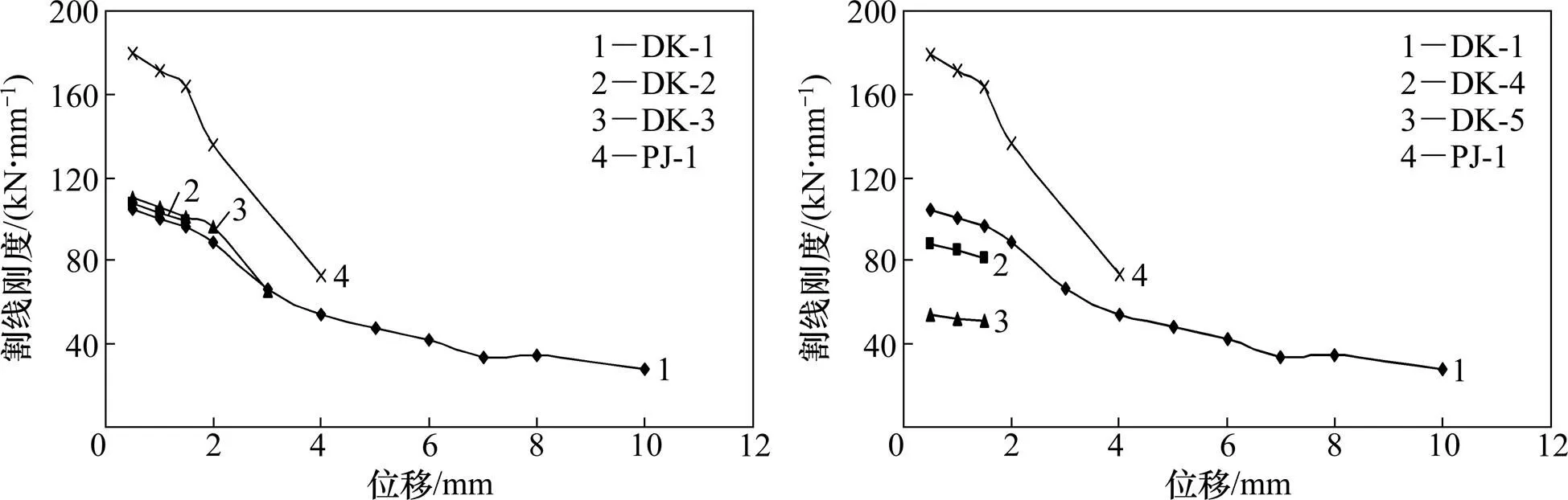
(a) 门洞位置变化；(b) 门洞尺寸变化

从图15可知：DK-1试件的滞回环面积较大，说明门洞开在墙体中间时，墙体有较强的耗能能力和变形能力，虽然门洞居中布置削弱了墙体的初始刚度，但在低周反复荷载作用下，墙体开裂后，门洞延缓了裂缝发展速度，达到极限荷载后，承载力逐渐下降，下降速度较缓慢。

从图16可看出：DK-1试件位移较大，但极限荷载较PJ-1试件的低，DK-2和DK-3试件在墙体开裂前发展速度相当，但DK-2试件的脆性破坏特征更明显，DK-4和DK-5试件的脆性破坏特征与DK-2试件基本相同，极限承载力和位移都很小。

从图17可知：开洞试件的初始刚度较无洞试件减小，且相差幅度很大。从图17(a)可看出：门洞位置的变化并不影响试件的初始刚度，但门洞离墙边越近，其刚度下降速度越快。从图17(b)可知：墙体的初始刚度随门洞尺寸的加大而减小，且下降幅度较大，门洞尺寸越大，墙体变形能力越小。

从以上分析可知：门洞位置及尺寸对墙体的受力影响显著；墙体的承载能力和延性随门洞尺寸的增大而减小；当门洞位置靠边布置时，承载力提高，而延性减小；当门洞居中布置时，墙体的变形能力较强，但承载力较小。

3 结论

1) 通过有限元模拟试验和已有试验结果的对比分析，本文提出的有限元分析方法具有一定的可行性和可靠性。

2) 墙体的承载能力随竖向压力的增加而显著提高，但当增加到一定程度时，承载力达到峰值；墙体的延性及破坏形式则随/m不同而不同，当/m＜0.21时，墙体为剪切破坏；当/m=0.09~0.10时，墙体延性最好；当0.21≤/m≤0.70时，墙体为剪压破坏；当/m≈0.50~0.60时墙体抗侧承载力及延性达到峰值；当/m≥0.70时，砌体为斜压破坏，实际工程中应避免此类破坏。

3) 墙体的抗侧承载力及初始刚度随砂浆强度等级的提高而增大，但延性性能劣化。在实际工程中，应结合经济效益，合理选用砂浆强度等级。

4) 门洞位置及尺寸对墙体的受力性能影响显著，开洞墙体的承载能力及延性较无洞墙体减小；当门洞居中布置时，墙体承载能力最小，而延性较好，而门洞靠边布置时，承载能力提高，延性减小；墙体的承载能力和延性则随门洞尺寸的增大而减小。因此，在抗震烈度较大的地区，门洞可适当地居中布置，在抗震烈度较小的地区，门洞可以靠边布置，同时应控制洞口的开洞率不超过30%；当洞口较大时，应采取加强构造措施。

[1] 宋岩丽, 耿震岗. 烧结煤矸石多孔砖外墙内保温研究[J]. 中北大学学报(自然科学版), 2012, 33(4): 480−484. SONG Yanli, GENG Zhengang. Study of internal thermal insulation of coal gangue porous brick walls[J]. Journal of North University of China (Natural Science Edition), 2012, 33(4): 480−484.

[2] 李景昆. 煤矸石页岩烧结多孔砖效益分析[J]. 墙材革新与建筑节能,2011, 17(7): 36−37. LI Jingkun. The benefit analysis of coal store-shale fired perforated brick[J]. Wall Material Innovation & Energy Saving in Buildings,2011, 17(7): 36−37.

[3] 常永贤. 煤矸石烧结多孔砖在双鸭山地区的应用[J]. 粉煤灰, 2001, 13(1): 27−28. CHANG Yongxian. Application of sintered porous gangue brick at Shuang Ya Shan area[J]. Coal ash China, 2001, 13(1): 27−28.

[4] 侯汝欣. 模数多孔砖砌体力学性能综合分析[J]. 四川建筑科学研究, 1996, 22(2): 9−12. HOU Ruxin. The comprehensive analysis of modulus of brick masonry mechanical properties[J]. Building Science Research of Sichuan, 1996, 22(2): 9−12.

[5] 阎开放. KP1型承重粘土空心砖墙片抗震性能试验研究[J]. 四川建筑科学研究, 1985, 11(1): 34−39. YAN Kaifang. The seismic behavior experimental research of KP-1 load-bearing clay hollow brick[J]. Building Science Research of Sichuan, 1985, 11(1): 34−39.

[6] 刘经纬, 董竟成, 沙安. 模数多孔砖墙体强度和变形的试验研究[J]. 建筑科学, 1994, 10(1): 31−36. LIU Jingwei, DONG Jingcheng, SHA An. The experimental study on the strength and deformation of the modulus of porous brick wall[J]. Building Science, 1994, 10(1): 31−36.

[7] 田春艳, 王宗纲, 聂建国. 多层混凝土小型空心砌块与煤矸石页岩多孔砖组合砌体模型楼动力性能实测与分析[J]. 地震工程与工程振动, 2003, 23(4): 105−110. TIAN Chunyan, WANG Zonggang, NIE Jianguo. Vibration test and analysis of a multi-storey small-sized concrete hollow block and shale -coal gangue porous brick mixed masonry structure[J]. Earthquake Engineering and Engineering Vibration, 2003, 23(4): 105−110.

[8] 梁建国, 湛华, 周江, 等. KP1型烧结页岩粉煤灰多孔砖墙体抗震性能试验研究[J]. 建筑结构, 2004, 34(9): 49−52. LIANG Jianguo, ZHAN Hua, ZHOU Jiang. The seismic behavior experimental research on the KP1 burned shale-farinose coal porous brick walls[J]. Building Structure, 2004, 34(9): 49−52.

[9] 刘小勤. 烧结煤矸石页岩多孔砖砌体局部受压试验研究[D]. 重庆: 重庆大学土木工程学院, 2002: 15−57. LIU Xiaoqin. Experimental study on local compression strength of fired shale-gangue perforated brick masonry[D]. Chongqing: Chongqing University. College of Civil Engineering, 2002: 15−57.

[10] 秦士洪, 皮天祥, 骆万康. 烧结页岩煤矸石多孔砖砌体抗压强度试验研究[J]. 建筑结构, 2005, 35(9): 3−6. QIN Shihong, PI Tianxiang, LUO Wankang. Experimental study on compression strength of fired shale-gangue perforated brick masonry[J]. Building Structure, 2005, 35(9): 3−6.

[11] 秦士洪, 胡珏, 骆万康, 等. 烧结页岩煤矸石多孔砖砌体抗剪强度试验研究[J]. 建筑结构, 2005, 35(9): 11−14. QIN Shihong, HU Jue, LUO Wankang, et al. Experimental study on shear strength of fired shale-gangue perforated brick masonry[J]. Building Structure, 2005, 35(9): 11−14.

[12] 李鹏. 煤矸石多孔砖墙体抗震性能试验研究[D]. 长春: 吉林大学建设工程学院, 2010: 23−38. LI Peng. Experimental Study on the seismic behavior of coal gangue brick wall[D]. Changchun: Jilin University. College of Architecture Engineering, 2010: 23−38.

[13] 赵成文, 周康, 高连玉. 煤矸石多孔砖砌体抗压强度试验研究[J]. 新型建筑材料, 2009, 36(7): 43−46. ZHAO Chengwen, ZHOU Kang, GAO Lianyu. Experimental study on compression strength of coal gangue brick masonry[J]. New Building Materials, 2009, 36(7): 43−46.

[14] 周万昊. 煤矸石多孔砖砌体基本力学性能及抗震性能试验研究[D]. 沈阳: 沈阳建筑大学土木工程学院, 2011: 39−53. ZHOU Wanhao. Experimental research on the basic mechanical behavior and seismic behavior of coal gangue brick masonry[D]. Shenyang: Shenyang Architectural University. School of Civil Engineering, 2011: 39−53.

[15] 徐爽. 煤矸石多孔砖砌体水平灰缝中钢筋锚固长度的试验研究[D]. 沈阳: 沈阳建筑大学土木工程学院, 2011: 27−42. XU Shuang. Experimental research on anchoring behavior of steel bar in grouted joint of coal gangue porous brick[D]. Shenyang: Shenyang Architectural University. School of Civil Engineering, 2011: 27−42.

[16] 梁海泉. 配筋煤矸石多孔砖砌体抗震性能研究[D]. 沈阳: 沈阳建筑大学土木工程学院, 2011: 41−60. LIANG Haiquan. Experimental research on the seismic behavior of masonry of reinforced coal gangue perforated brick[D]. Shenyang: Shenyang Architectural University. School of Civil Engineering, 2011: 41−60.

[17] 吕伟荣, 施楚贤. 剪压复合作用下普通砖气体的ANSYS分析[C]//顾祥林, 高连玉. 2005年全国砌体结构基本理论与工程应用学术会议论文集. 上海: 同济大学出版社, 2005: 126−130. LÜ Weirong, SHI Chuxian. Analysis of mechanical performance for fired common brick masonry under combined shear and compression using ANSYS[C]//GU Xianglin, GAO Lianyu. Proceedings of the 2005 National Conference on Masonry Theory and Application. Shanghai: Tongji University Press, 2005: 126−130.

[18] 刘桂秋, 施楚贤, 刘一彪, 等. 砌体受压应力−应变关系[C]//现代砌体结构. 2000年全国砌体结构学术会议论文集. 北京: 中国建筑工业出版社, 2000: 12−18. LIU Guiqiu, SHI Chuxian, LIU Yibiao, et al. A generic stress-strain equation for masonry materials in compression[C]// Proceedings of the 2000 National Conference on Masonry Structure. Beijing: China Architecture & Building Press, 2000: 12−18.

[19] 黄艳, 阚明辉, 王自法. 单调及低周往复荷载作用下砌体非线性分析[J]. 世界地震工程, 2012, 28(1): 135−141. HUANG Yan, KAN Minghui, WANG Zifa. Nonlinear analysis of masonry under monotonic and low cyclic loading[J]. World Earthquake Engineering, 2012, 28(1): 135−141.

[20] GB 50003—2001. 砌体结构设计规范[S]. GB 50003—2001. Code for design of masonry structures[S].

(编辑 罗金花)

Analysis on mechanical behavior influence factor of gangue hollow brick wall under the horizontal loads

LU Linfeng1, ZHANG Yaping2

(1. School of Civil Engineering, Chang’an University, Xi’an 710061, China;2. Guangdong China Engineering Design Co Ltd., Sichuan, Chengdu 610084, China)

On the basis of existing seismic tests of gangue hollow brick wall, the finite element model was established by using ANSYS, and the analysis results were compared with test results to verify the correctness of the finite element model. Many parameters were considered in exploring the impacts of parameter variations on the mechanical behaviors of gangue hollow brick walls under horizontal loads, such as the vertical pressure, the strength classes of mortar, size of openings and position of openings. Twenty-three specimens of three series were designed for finite element simulation analysis to research the mechanical behaviors of each specimen under monotonic and low cyclic loads. The results show that the vertical pressure is the main influencing factor on mechanical behavior of hollow brick wall. The bearing capacity of the wall improves with the increase of the vertical pressure, but the ductility and failure mode of the walls show different forms with the ratio change of vertical compressive stress and average compressive bearing capacity. The bearing capacity of the wall improves with the increase of the mortar strength, but the ductility decreases. The size and position of the structural opening are also the main influencing factor on mechanical behavior of hollow brick wall. The ultimate bearing capacity, rigidity and ductility of the wall decrease with the increase of the structural opening size. When the structural opening is arranged at the center, the bearing capacity is the minimum, and the ductility is better. When the structural opening is arranged aside, the bearing capacity of the wall increases, and the ductility decreases.

gangue hollow brick wall; ultimate bearing capacity; ductility factor; hysteretic behavior

10.11817/j.issn.1672-7207.2015.06.040

TU391；TU317.1

A

1672−7207(2015)06−2274−11

2014−09−15；

2014−11−20

中央高校基本科研业务费专项资金资助项目(CHD2012TD012)(Project (CHD2012TD012) supported by the Fundamental Research Funds for the central Universities)

卢林枫，博士，副教授，从事新型结构体系结构分析与设计研究；E-mail：54LLF@163.com