各向异性花岗岩的力学参数及相关性

吴秋红，尤明庆，苏承东



各向异性花岗岩的力学参数及相关性

吴秋红1，尤明庆2，苏承东2

(1. 中南大学资源与安全工程学院，湖南长沙，410083；2. 河南理工大学能源科学与工程学院，河南焦作，454010)

对花岗岩块及试样进行纵波速度测试、单轴压缩和巴西劈裂试验，确定材料的力学性质参数之间的关系。研究结果表明：花岗岩具有均匀、各向异性特征；岩石内裂隙面存在优势方向，沿其法向的纵波速度、抗拉强度及压缩弹性模量均较低，但单轴抗压强度未受其影响反而较高；另一方向的抗压强度因试样易于沿裂隙面劈裂而偏低，其他参数则较高，由此引起试样单轴抗压强度与弹性模量、纵波速度呈负相关性。

岩石力学；各向异性；超声波速度；力学参数

岩石力学性质参数之间的关系尤其是超声波速度与单轴抗压强度、弹性模量、巴西劈裂强度的关系一直是室内实验的研究内容之一。超声波测试便利，可以对岩体进行大范围无损检测，因而，理解超声波速度与岩体强度和变形参数之间的关系具有重要理论意义和工程应用价值[1−8]。岩石种类繁多、结构复杂，力学参数之间的关系至今尚未明确，如：依据超声波速度求得的动态参数与单轴压缩得到的弹性模量(平均模量、变形模量)之间的关系不明确[9]；强度和弹性模量较高的花岗岩纵波速度通常在6 km/s 以下[1,10]，而强度和弹性模量较低的大理岩纵波速度可以达到7 km/s以上[2]。即使对同一种岩石，纵波速度与岩石的单轴抗压强度甚至可以具有负相关性。尤明庆等[11]给出了大理岩压缩损伤和砂岩热损伤测试结果，说明纵波速度、弹性模量和强度是岩石试样力学性质的不同宏观表现，三者通常具有正相关性，但并没有确定的力学关系，且例外情形大量存在。需要针对引起岩石损伤的具体过程，利用多种手段具体研究岩石内部的结构变化。岩石是矿物颗粒的集合体，在微观乃至宏观上具有非均质性和各向异性，并非理想线弹性体。花岗岩由岩浆冷凝而成，而冷凝是逐步发生的，内部颗粒排列、裂隙分布等随方向而变化，引起力学参数的宏观各向异性。本文测试同一花岗岩块3个方向的超声波速度，并沿岩块2个方向加工试样，测试纵波速度后，进行单轴压缩、巴西劈裂试验，研究岩石力学性质参数之间的关系。

1 花岗岩矿物成分各向异性分析

花岗岩块产自河南省辉县，为灰白色，显晶质结构，块状构造，长为600 mm，高为149 mm，宽为82 mm，密度为2 610 kg/m3，孔隙率为1.04 %(吸水率为0.40 %)，如图1所示。

图1 岩块示意图

岩块主要矿物为钠长石、石英、黑白云母，含少量角闪石，由于这些矿物成分都具有特定的晶体结构，除了石英无解理外，其他矿物成分都有解理[12]。晶体的矿物成分在一定程度上决定了微观裂隙的发展方向，影响岩石在成岩过程中的各向异性，同时，上述矿物的晶体具有板状、片状，这种结构本身就具有一定程度的各向异性，而大量的类似晶体排列组合就会形成明显的各向异性集合体。花岗岩试样如图2所示。从图2可明显看到类似的弱面结构，微观的各向异性引起力学参数的宏观各向异性。

图2 花岗岩试样

2 岩块及试样纵波速度测试结果

对图1所示岩块沿长度方向加工成4个直径为50 mm、高度为100 mm的圆柱试样和4个直径为50 mm、厚度为30 mm左右的圆盘试样；沿高度方向加工成4个与长方形相同尺寸的圆柱试样和8个圆盘试样，利用RMT-150B试验机进行轴向压缩，采用速率为0.002 mm/s变形控制加载。圆柱试样的端面不平度小于 0.05 mm；对圆盘试样的2个端面也进行磨削加工，端面不平度小于 0.1 mm。

试样制备后在室内自然干燥7 d，采用UTA−2000A超声波测试仪，加工前先测量岩块的纵波速度，后测量加工的圆柱试样纵波波速。

从岩块的长度、高度和宽度3个方向各取3个测点测量3个方向的纵波速度，沿同一方向纵波通过岩块的速度P1相对误差在3%之内，而不同方向的差异较大：沿长度、高度和宽度方向的纵波速度平均值分别为4.224，3.224和3.791 km/s；沿长度和高度方向的纵波速度差异达到30 % 以上。花岗岩具有显著的均匀、各向异性特征。

3 巴西劈裂试验结果

加载压头为平板，其与试样的接触状态介于圆弧压头和钢针之间，两者分别由国际岩石力学学会[13]和中国水利水电学会[14]所推荐。长度、高度和宽度方向的12个圆盘岩石抗拉强度如表1所示。

表1中，长度方向试样沿高度方向钻取，沿宽度方向加载，破裂面法向为长度方向，强度为12.5~14.7 MPa，平均为13.4 MPa，变化幅度为17.6%；高度方向试样沿长度方向钻取，沿宽度方向加载，破裂面法向为高度方向，强度为9.5~11.8 MPa，平均为10.8 MPa，变化幅度为24.9%；宽度方向试样沿高度方向钻取，沿长度方向加载，破裂面法向为宽度方向，强度为12.2~13.8 MPa，平均为13.2 MPa，变化幅度为13.1%。

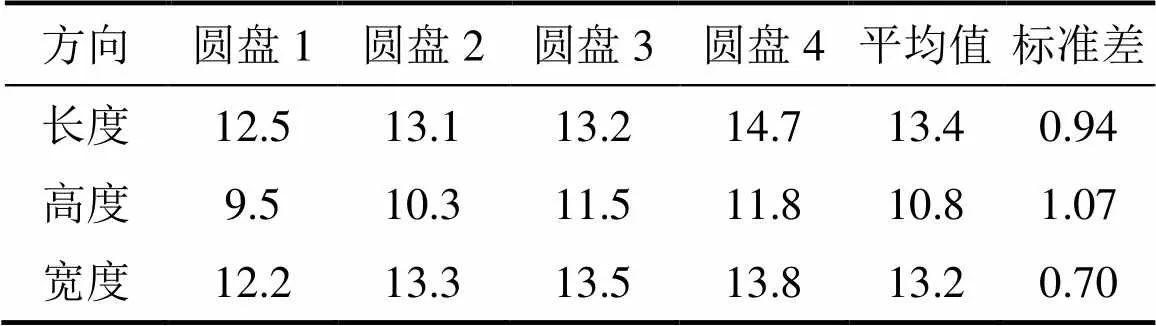
表1 圆盘沿3个方向巴西劈裂的强度

同一方向的4个圆盘劈裂强度偏差系数在10% 以下；长度和宽度方向的强度大致相当，而方向的劈裂强度偏低达2.6 MPa。

圆盘的劈裂强度与破裂方式有关。图3所示为4个圆盘破坏后的照片。从图3可见：强度较低的2个圆盘 H1和H2 破裂面较平整；强度较高的试样B2破裂面仅一侧平整，另一侧有多个碎块；强度最高的试样L4中出现众多碎块，缺乏明显的主控破裂面。垂直于方向的裂隙面可以使圆盘规则破裂，而抗拉能力均匀的材料使岩石强度提高，且出现多处破裂。

试样：(a) H1；(b) H2；(c) B2；(d) L4

4 单轴压缩试验结果

单轴压缩得到的轴向应力−应变曲线见图4，相关力学参数见表2。表2中，弹性模量是应力−应变曲线上最大应力的30%和70%这2点的割线斜率，大致相当于平均模量，s为峰值强度。

表2 花岗岩试样单轴压缩试验结果

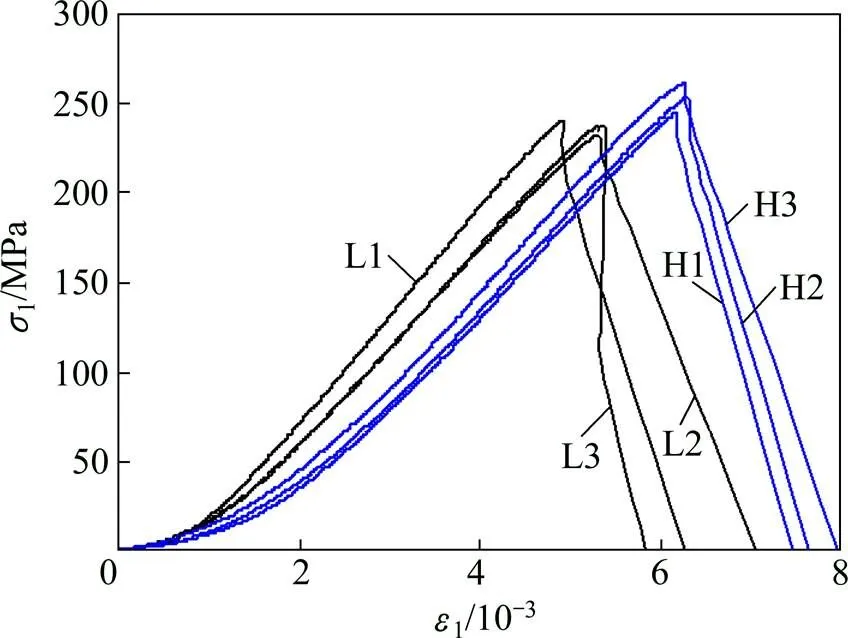
图4 花岗岩试样单轴压缩应力−应变全程曲线

从图4可以看出：2组试样在单轴压缩时变形特征大致相同，均表现出较强的脆性特征；同一方向的力学参数差异较小，但具有明显的方向性；在和这2个方向花岗岩的强度和弹性模量具有负相关性。此外，方向试样在压缩初期变形是非线性的，体现了裂隙逐步闭合的过程。

圆柱试样的纵波速度P2见表2。从表2可见：同一方向加工的圆柱试样的纵波速度差异在2%之内，与仪器的测试精度相当；而方向的平均值为4.003 km/s，方向的为3.087 km/s，差别较大。

图5所示为试样L3和H2破坏后的照片。从图5可以看出：试样L3有明显的剪切面，局部有劈裂面，是剪切和张拉破坏的结果；试样H2有较多的劈裂面。岩石在达到峰值强度后，承载能力迅速降低，试样破坏时伴随巨大的响声，局部被压成粉末状。

试样：(a) L3；(b) H2

L2和H1试样中部两侧各粘贴栅长为10 mm、栅宽为2 mm的2片应变片，标号分别为G1，G2，G3和G4，测量局部变形，见图6。由于花岗岩内不同矿物颗粒的变形特征不同，因而应变片测得的变形随位置变化而变化。此外，相同应力下应变片测量值明显低于LVDT位移传感器测量值，后者包含试样内部裂隙、弱面闭合以及试样端部不整等引起的非线性变形。临近峰值应力时，在应变片断裂未能测得峰值应变。

(a) L2；(b) H1

从图6可以看出：试样H1试样具有明显的非线性变形特征，存在裂隙闭合过程，但强度较高；而试样L2 局部变形没有体现裂隙的闭合过程，但其强度较低。这进一步说明花岗岩试样具有明显方向性。

5 各向异性分析

超声波测试和单轴压缩的试验结果表明：在试验粒度为5 cm的花岗岩具有较好的均质性，但具有明显的各向异性特征。3个方向的各个力学参数平均值见表3。

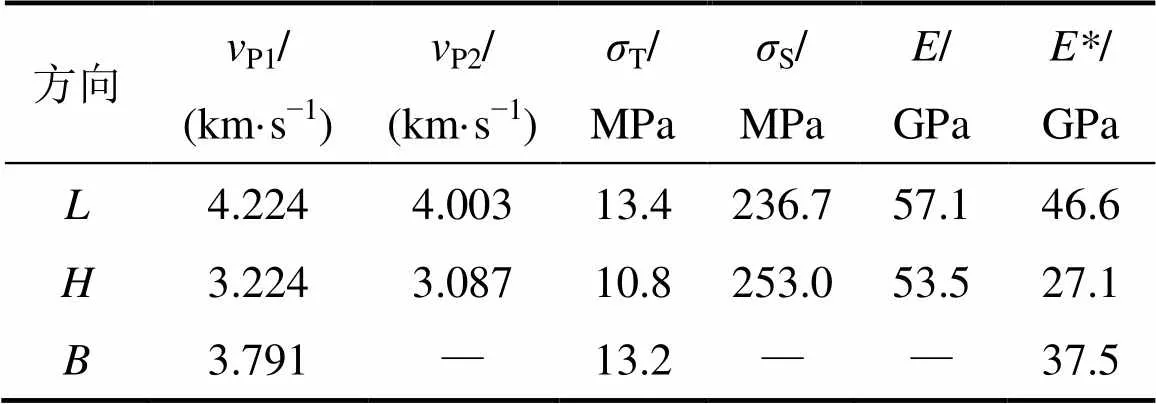
表3 花岗岩3个方向的力学参数平均值

杆件在横向的自由膨胀使材料刚度降低，因而沿杆件传播的纵波速度小于无限体中的速度，比值为，与泊松比有关：在=0.20时该值为0.95，=0.30时为0.86。直径为50 mm、高度为100 mm的圆柱试样尽管并非杆件，但所用超声波频率为 50 kHz，波长达 7 cm左右，与试样直径相当，因而，岩样中波速低于大尺度岩块中波速5%左右。岩块中纵波的速度大于平面纵波速度，动态弹性模量满足

其中：为密度；P1为岩块纵波速度。基于P1计算的*见表3。显然，岩石的动态模量低于其轴向压缩试验得到的平均模量。

从表3可以看出：方向的纵波速度、抗拉强度和弹性模量都较高，而单轴抗压强度偏低；方向则与之完全相反。其原因是：花岗岩尽管孔隙率仅为1.04%，但内部颗粒间的裂隙具有较大面积；裂隙面的优势延展方向垂直于，因而方向的劈裂强度、纵波速度较低；试样沿方向压缩时也具有明显的裂隙闭合过程(图4)，平均模量、初始切线模量均较低。

沿方向的纵波和巴西劈裂以及轴向变形受上述裂隙的影响较小；而岩石单轴压缩破坏与侧向劈裂有关，强度会受到裂隙的影响而偏低。

比较方向和方向的力学参数可以发现：岩石内众多分布微小裂隙对单轴压缩和弹性模量影响较小，但对超声波速度和动态模量影响较大；超声波速度表示岩石在微小载荷作用下的变形特征，对应于岩石的初始切线模量，与单轴抗压强度、平均模量以及抗拉强度并没有直接的力学关系。岩石的单轴抗压强度可以与弹性模量、纵波速度具有负相关性。当然，基于试验结果可以研究这些参数之间的统计关系，但对其适用性需要进一步研究。

6 结论

1) 纵波速度、巴西劈裂强度、单轴抗压强度及弹性模量均表明试验用花岗岩具有较好的均质性和各向异性特征。

2) 花岗岩孔隙率为1.04%，但可以具有较大的裂隙面积。若裂隙面存在优势方向，则沿其法向的纵波速度、抗拉强度及压缩弹性模量将较低，但单轴压缩强度所受影响较小；另一方向的抗压强度因试样易于沿裂隙面劈裂而偏低，其他参数则较高。

3) 岩石力学参数之间的相关性需要依据岩石内部构造进行具体分析。岩石的单轴抗压强度与弹性模量、纵波速度具有负相关性。

[1] 陈颙, 黄庭芳. 岩石物理学[M]. 北京: 北京大学出版社, 2001: 41−68.CHEN Yong, WONG Tengfong. Rock physics[M]. Beijing: Peking University Press, 2001: 41−68.

[2] 王让甲. 声波岩石分级和岩石动弹性力学参数的分析研究[M]. 北京: 地质出版社, 1997: 13−19.WANG Rangjia. The acoustic classification of rocks and study of dynamic-elastic mechanical parameters of rocks[M]. Beijing: Geological Publishing House, 1997: 13−19.

[3] 丁梧秀, 姚增, 蒋振. 岩体工程特性研究中弹性波速参数取值方法探讨[J]. 岩土力学, 2004, 25(9): 1353−1356.DING Wuxiu, YAO Zeng, JIANG Zhen. Study on methods of how to select reasonably elastic wave velocity parameters of engineering rockmass[J]. Rock and Soil Mechanics, 2004, 25(9): 1353−1356.

[4] LI Qiyue, DONG Longjun, LI Xibing, et al. Effects of sonic speed on location accuracy of acoustic emission source in rocks[J]. Transactions of Nonferrous Metals Society of China, 2011, 21(12): 2719−2726.

[5] 陈庆发, 周科平, 胡建华, 等. 缓倾薄层弱结构松动圈声波测试时测孔布置的理论依据与验证[J]. 中南大学学报(自然科学版), 2009, 40(5): 1406−1410.CHEN Qingfa, ZHOU Keping, HU Jianhua, et al. Theory basis and practice of acoustic measuring boreholes arrangement for broken rock zone in gently inclined thin layer weakness structure[J]. Journal of Central South University (Science and Technology), 2009, 40(5): 1406−1410.

[6] 邓华锋, 李建林, 邓成进, 等. 岩石力学试验中岩样选择和抗压强度预测方法研究[J]. 岩土力学, 2011, 32(11): 3399−3403. DENG Huafeng, LI Jianlin, DENG Chengjin, et al. Analysis of sampling in rock mechanics test and compressive strength prediction methods[J]. Rock and Soil Mechanics, 2011, 32(11): 3399−3403.

[7] 邓涛, 黄斌彩, 杨林德. 致密岩石纵横波速各向异性的比较研究[J]. 岩土力学, 2007, 28(3): 493−498.DENG Tao, HUANG Bincai, YANG Linde. Anisotropy comparison of P wave and S wave velocity for compacted rocks[J]. Rock and Soil Mechanics, 2007, 28(3): 493−498.

[8] 江进, 孙进忠, 乔艳红, 等. 太原晋阳西山大佛岩石动静力学参数的对比研究[J]. 岩石力学与工程学报, 2007, 26(Z1): 3452−3460. JIANG Jin, SUN Jinzhong, QIAO Yanhong, et al. Comparison between static and dynamic parameters of grand buddha rockmass specimens in west Jinyang Mountain in Taiyuan[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(Z1): 3452−3460.

[9] 尤明庆, 苏承东, 杨圣奇. 岩石动静态参数间关系的研究[J]. 焦作工学院学报, 2002(6): 413−419.YOU Mingqing, SU Chengdong, YANG Shengqi. Relation between static and dynamic parameters of rocks[J]. Journal of Jiaozuo Institute of Technology, 2002, 21(6): 413−419.

[10] 尤明庆, 苏承东, 申江. 岩石材料的非均质性与动态参数[J]. 辽宁工程技术大学学报, 2001, 20(4): 492−494. YOU Mingqing, SU Chengdong, SHEN Jiang. Effect of heterogeneity on the dynamic parameters of rocks[J]. Journal of Liaoning Technical University, 2001, 20(4): 492−494.

[11] 尤明庆, 苏承东, 李小双. 损伤岩石试样的力学特性与纵波速度关系研究[J]. 岩石力学与工程学报, 2008, 27(3): 458−467. YOU Mingqing, SU Chengdong, LI Xiaoshuang. Study on the relation between longitudinal wave speed and mechanical properties of damaged specimens[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(3): 458−467.

[12] 车树成, 张荣伟. 煤矿地质学[M]. 徐州: 中国矿业大学出版社, 1996: 38−65. CHE Shurong, ZHANG Rongwei. Coal mine geology[M]. Xuzhou: China University of Mining and Technology Press, 1996: 38−65.

[13] Bieniawski Z T, Hawkes I. Suggested methods for determining tensile strength of rock materials[J]. International Journal of Rock Mechanics and Mining Sciences, 1978, 15(1): 99−103

[14] SL 264—2001, 水利水电工程岩石试验规程[S].SL 264—2001, Specifications for rock tests in water conservancy and hydroelectric engineering[S].

(编辑 陈灿华)

Mechanical parameters and their relativity of anisotropy granite

WU Qiuhong1, YOU Mingqing2, SU Chengdong2

(1. School of Resource and Safety Engineering, Central South University, Changsha 410083, China;2. School of Energy Science and Engineering, Henan Polytechnic University, Jiaozuo 454010, China)

Longitudinal wave measurement, uniaxial compression and Brazilian split test were carried out for granite to study the relationship among rock mechanical parameters. The results show that granite is homogenous but anisotropy significantly. The fissure planes in the granite have a predominance normal direction, along which the longitudinal wave velocity, tensile strength and elastic modulus are lower, but the uniaxial compression strength may have high magnitude. The fissures induce axial split and result in the uniaxial compression strength decease along the direction within their plane, but do not influence the other parameters observably. Therefore, uniaxial compression strength of the granite has negative correlation with elastic modulus and longitudinal wave velocity.

rock mechanics; anisotropy; supersonic velocity; mechanical parameters

10.11817/j.issn.1672-7207.2015.06.032

TU443

A

1672−7207(2015)06−2216−05

2014−06−22；

2014−08−25

国家自然科学基金资助项目(10572047)(Project (10572047) supported by the National Natural Science Foundation of China)

吴秋红，博士研究生，从事岩石动力学研究；E-mail：0507010223@163.com