端铣刀五坐标曲面加工刀位计算方法研究

□ 丁 杰 □ 孙 博 □ 刘践丰 □ 李 鑫

1.北京石油化工学院 北京 102617 2.抚顺石化公司烯烃厂 辽宁抚顺 113004 3.河北石油职业技术学院 河北廊坊 065000

端铣刀五坐标曲面加工刀位计算方法研究

□ 丁 杰1□ 孙 博2□ 刘践丰1□ 李 鑫3

1.北京石油化工学院 北京 102617 2.抚顺石化公司烯烃厂 辽宁抚顺 113004 3.河北石油职业技术学院 河北廊坊 065000

提出端铣刀五坐标曲面加工刀具干涉情况，分析了刀具后跟脚和刀位的计算过程，采取了误差补偿方法，有效解决了端铣刀五坐标曲面数控加工的技术难点，为数控加工提供了技术参考，具有现实意义和实际应用价值。

五坐标 端铣 刀位

近年来，五坐标端铣加工在曲面加工中的应用日益广泛,已成为数控领域的研究热点,越来越多的复杂曲面零件需用多坐标数控机床进行加工。而刀具与加工表面的几何拟合关系非常复杂，当被加工表面的曲率半径小于刀具半径时,刀具和被加工表面间就会发生曲率干涉，有时尽管被加工表面的曲率半径大于刀具半径,但仍有可能发生刀具过切被加工表面的现象［1］。因此在空间自由曲面五坐标数控加工中,如何确定各类刀具的无干涉刀位轨迹,至今仍是一个难题。由于快速进给铣刀具有很多优点,对它的曲面端铣加工刀位进行研究计算就变得十分重要，在端铣刀五坐标端铣数控加工中，刀具与加工表面的几何拟合关系非常复杂，是五坐标端铣数控加工及编程技术的关键。

1 基本原理

采用端铣刀加工曲面零件时，为了避免刀具底面中心与加工表面接触以及切削刃与加工表面发生干涉，应将刀轴置于加工表面法向矢量n与进给方向切向矢量f所在的平面n-f之内，五坐标加工刀具位置如图1所示，n-f即为端铣加工时刀具的摆动平面，刀具底面的刀刃外圆或刀刃外圆环面与加工表面接触，同时刀轴将沿进给方向与加工表面法向矢量倾斜一个角度β，β角称为后跟角，图中，R为刀具半径，R1为环形刀刃圆弧半径，Re＝R-R1（1-sinβ）为端铣加工时环形刀的有效切削半径。如果刀具的有效切削半径大于被加工曲面的曲率半径，则会发生切削干涉，可以通过加大平头刀的倾角，以减小有效切削半径，避免干涉的发生。

2 后跟角计算

在端铣刀五坐标端铣数控加工中，刀具与加工表面的几何拟合关系及后跟角的大小与加工表面的形状密切相关。将端铣刀刀具半径简化为Re，以加工表面微分几何结构为凹椭圆点表面（即加工表面的主曲率k1和k2都大于零）为例［2，3］，介绍五坐标端铣后跟角的计算方法。

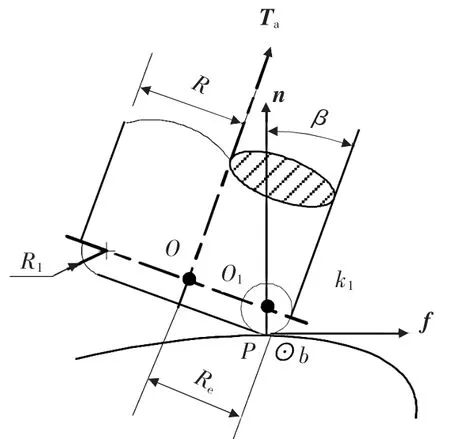
▲图1 五坐标加工刀具位置

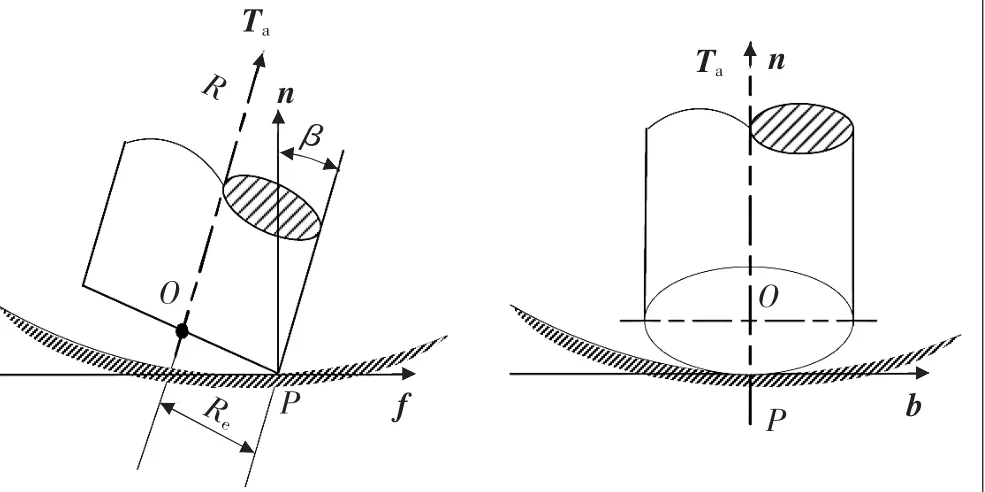
▲图2 端铣刀与凹椭圆点曲面的关系

设端铣刀与加工表面切触于P点，在P点建立一个局部坐标系，刀具与加工表面在该局部坐标系中的投影关系、端铣刀与凹椭圆点曲面的关系如图2所示，其中Re为端铣刀刀具半径，Ta为单位刀轴矢量，n和f分别为加工表面在P点处的单位法向矢量和沿进给方向的单位切向矢量，b=f×n，kb和kf分别为加工表面在P点处沿b方向和f方向的法曲率。则在该局部坐标系内，刀盘底面方程为：

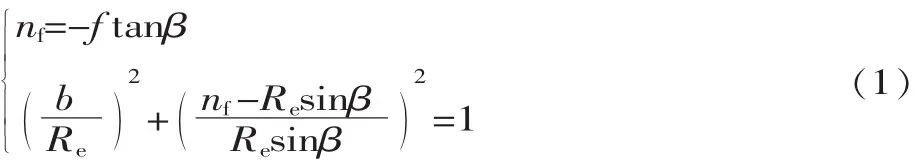
加工表面的局部二阶逼近方程为：

式中：L、M、N为加工表面在P点处以f、b为参数的第Ⅱ类微分基本量，即：

L=rff″n=kfE=kfrf′rf′=kf，M=rff″n，N=rbb″n=kbF=kbrb′rb′= kb，r为加工表面的参数表示r（f，b）。

设H为端铣刀刀盘底面距加工表面的法向高度：

很显然，刀盘不切入加工表面的充分必要条件为：

H≥0

为了简化处理问题，用H在摆刀平面（n，f平面）及其法平面（n，b平面）上的投影关系构造如以下两个必要条件：

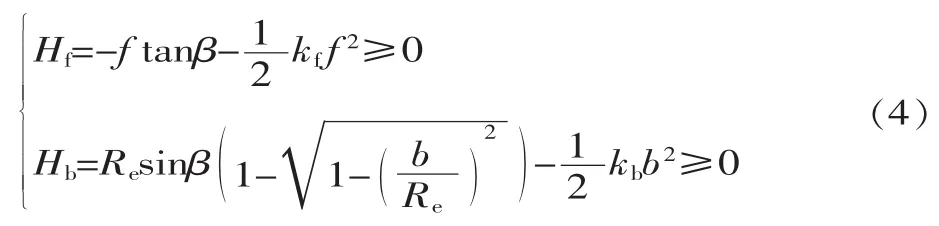
进一步推导，可得：

令-f=2Recos茁，b=0，可得：

实际应用中，对于曲面r（u，v），曲面沿其参数线方向ru和rv的法曲率ku和kv，以及曲面的主曲率k1和k2的求解较为容易，如果曲面的曲纹坐标（u，v）不正交的话（一般情况下不正交），即使是沿参数线加工，kb的求解（kf等于ku或kv中的一个）也是相当困难的，原因在于这时曲面的主方向的求解比较困难。因此，上面的条件式须作进一步简化。

取ke=max（k1，k2），将式（6）简化为：

实际应用中，由于环形刀的有效切削半径Re是随后跟角的变化而变化的，可用刀具半径R代替，并取端铣后跟角：

根据微分几何理论，很容易求出切触点处的曲面的主曲率k1和k2，根据k1和k2的不同数值组合，可将加工表面分为不同的微分几何结构。下面分别给出各种微分几何结构下的后跟角茁的计算公式。

（1）对于凹椭圆点（k1>0，k2>0）、双曲线点（k1>0，k2<0）、凹抛物点（k1>0，k2=0）：茁=arcsin（keRe）+2°，ke= max（k1，k2）。

（2）对于凸抛物点（k1=0，k2<0）、凸椭圆点（k1<0，k2<0），取端铣后跟角茁=2°。

3 刀位计算方法

五坐标端铣加工的刀位是指端铣刀刀盘上刀刃圆环中心点的坐标及刀轴矢量，如图1中O点的坐标及矢量Ta。

式中：PQ=rn；QO=（R-r）（nsin茁-fcos茁）；ro为O点的矢径，rp为P点的矢径。

令：

则：

式中：u、v为加工表面的曲纹坐标参数，ru′=坠r/坠u、rv′=坠r/坠v。

4 加工误差补偿

首先讨论加工轨迹为凸曲线的情况。当kf<0时，加工表面沿走刀方向为凸曲线，而由上面的误差分析可知，刀具切触点的轨迹为凹曲线。因此加工误差较大，为直线逼近误差与刀轴摆动误差绝对值之和，即：

如图3所示，将刀具切触点A沿加工表面外法向矢量移动到A′点，使：

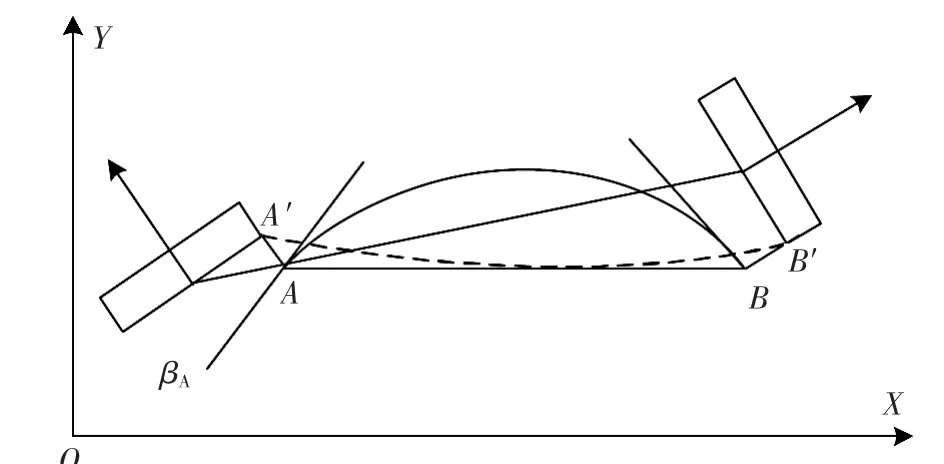
▲图3 刀具切触点偏置法补偿加工误差

即用A′代替A作为新的刀具切触点，驻兹表示接触点之间的夹角，这样，加工误差的分布发生了改变，从而达到了加工误差补偿的目的。当kf>0时，加工曲面沿进给方向为凹曲线，而刀轴摆动误差|啄n|小于直线逼近误差|啄t|，因此在任何情况下都不会发生超差，故无须进行加工误差补偿。

5 结论

刀片的几何形状近似凸三角形,切削刃被设计成一个很大的圆角，其切削深度很小,使得切削力的方向是朝向主轴的轴向,这在悬伸较长的情况下非常有利,能使用非常高的进给量而没有太大的振动,可以大大提高加工效率。在对快速进给铣刀五坐标端铣加工技术进行研究的基础上,给出了完整准确的刀位计算公式,为快速进给铣刀的实际应用提供了理论支持。

［1］ 李立杰,王珉.空间自由曲面五坐标数控加工无干涉刀位轨迹生成算法［J］.航空制造技术，1999（3）：35-37.

［2］ 樊文刚,王小椿.快速进给铣刀五坐标端铣加工刀位计算［J］.北方交通大学学报，2010（1）：154-157.

［3］ 王清辉，廖文和，刘壮，等.五坐标数控加工刀位轨迹及其干涉检查的算法研究［J］.航空学报，1997,18（3）：330-335.

［4］ 喻道远，钟建琳，熊壮，等.空间自由曲面数控编程中刀位轨迹的计算方法及存在的问题 ［J］.制造业自动化，1997（1）：25-28.

（编辑 小 前）

TH161；TG502 %

A

1000－4998穴2015雪07－0058－03

2015年1月