含非阿基米德无穷小量ε的CCR模型应用研究

黎　薇，杨　辉

（1.铜仁学院 数学科学学院，贵州 铜仁 554300；2.贵州大学 理学院，贵州 贵阳 550025 ）

含非阿基米德无穷小量ε的CCR模型应用研究

黎薇1，杨辉2

（1.铜仁学院 数学科学学院，贵州 铜仁 554300；2.贵州大学 理学院，贵州 贵阳 550025 ）

在“相对有效评价”的基础上，引入含有非阿基米德无穷小量ε的CCR经典模型，结合线性规划的单纯形算法，用LINGO软件求解结果，根据结果判断决策单元是否DEA有效。本文应用上述方法对贵州某高校学的教学质量和农业银行营业点经济效率规模的有效性评价。

数据包络分析（DEA）；CCR模型；多目标决策

1.经典的CCR模型［1，2］

设有n个待评价决策单元是有效性的：DMUj，j=1，2，…，n ，θ为DMUj效率评价参数。设每个决策单元有m项输入，s项输出，即：

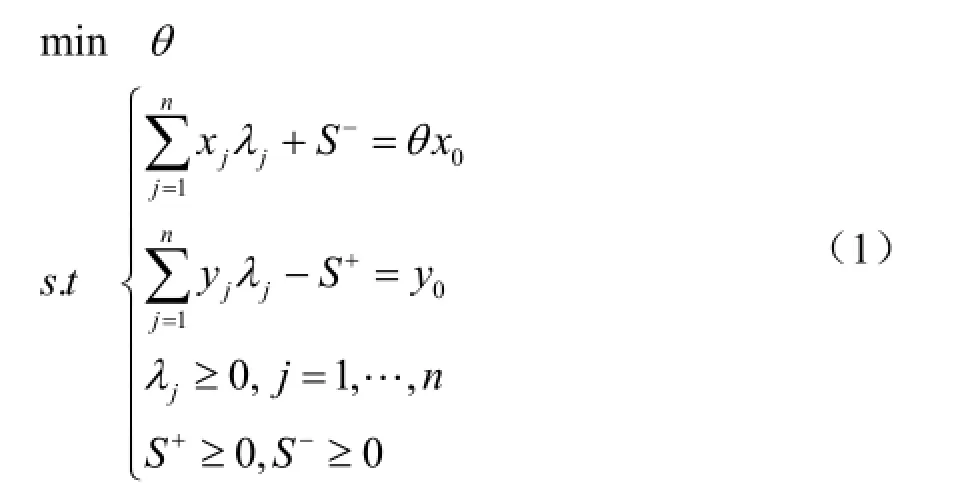
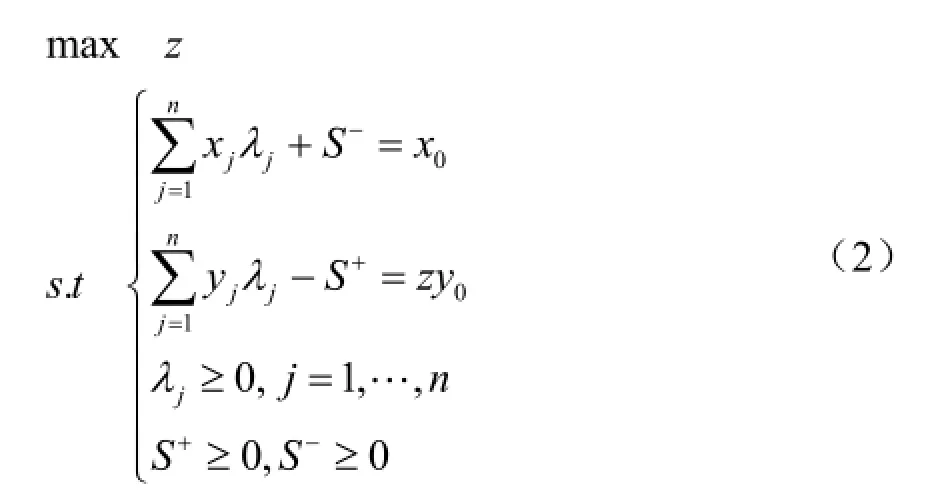
说明：上面公式（1）为输入模型，思考在输出不减的情况下输入量是否能减少到最小；（2）式为输出模型，思考在输入不增的情况下输出量是否能增加到最大。

总之，CCR模型是规模收益不变的，用来评价决策单元输出和输入模式的有效性。

2.含非阿基米德无穷小量ε的CCR模型［3，4］

DEA最早是一种单目标预测决策单元的有效性的方法，随着时代发展扩展为一种多输入多输出同类决策单元的效率有效性评价方法。预测出同类型投入产出DMUj的相对最高效率。但它只能从投入或产出两种角度先后来预测决策单元的相对有效性，而不能同时进行预测。决策单元是否相对有效还须在相应的规划中引入非阿基米德无穷小量才能做出判断。

在评价相对有效性的基础之上，可以考虑引入非阿基米德无穷小量ε，这样就可以用线性规划中的单纯形算法求解CCR模型，用这样的模型可以判断DMUj的DEA有效。

在广义实数域内，非阿基米德无穷小量ε是一个数，它小于任何正数且大于零［5］。思考含非阿基米德无穷小量ε的CCR模型：

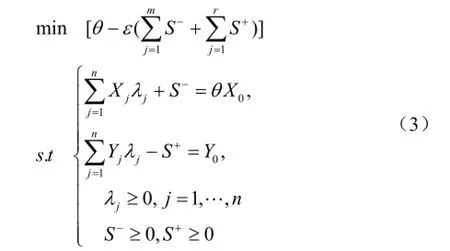
其中θ为决策单元DMUj的效率评价参数，xj为DMUj的投入要素的集合，Yj为DMUj的产出要素的集合，λj为决策单元DMUj的组合比例，S-、S+为松弛变量，x0、y0为DMUj的投入向量和产出向量。由此模型，可以判断出DMUj是否DEA有效，还是仅为弱DEA有效或者是非DEA有效。

3.DEA有效性的判断

对具有非阿基米德无穷小量的CCR输入模型，可以根据以下规则判断DEA有效性：

（1）若θ＜1，则DMUj为非DEA有效；

（2）若θ=1，且 S-=S+=0时，则DMU为DEAj有效：即在这n个决策单元组成的系统中，在原投入 x0的基础上所获得的产出 y0已达到最优；

（3）若θ=1，且 S-≠S+≠0 则DMUj为弱DEA有效：即在这n个决策单元组成的模型中投入量 x0可减少S-而保持 y0原产出不变，或在投入 x0不变的情况下可将产出提高S+。

求解含非阿基米德无穷小量ε的DEA模型时，可令ε=10-5，接下来利用LINGO软件求解，根据求解结果判断决策单元是否DEA有效。

4.实际例子应用

例 1 投入多少教育经费，达到怎样的实际效果是大学教育管理者关心的问题。这需要结合当地教学水平、资金能力及学生本身学习能力等因数来决定投入规划。最新的教学理念和充足的经费投入能够在很大程度上调动教师教学和学生学习的主动性，能够明显提高教学质量，培养更多的优秀人才。下面用含非阿基米德无穷小量的CCR模型来探讨投入的有效性。

运用模型对教学效果进行有效性的评价，首先要确定教学的投入产出指标量。选择某校数学科学学院2009年～2011年间的教育经费、教师人数和图书经费作为投入指标量，毕业生就业数、考取研究生数作为教学的产出指标量，具体数据如表1所示。

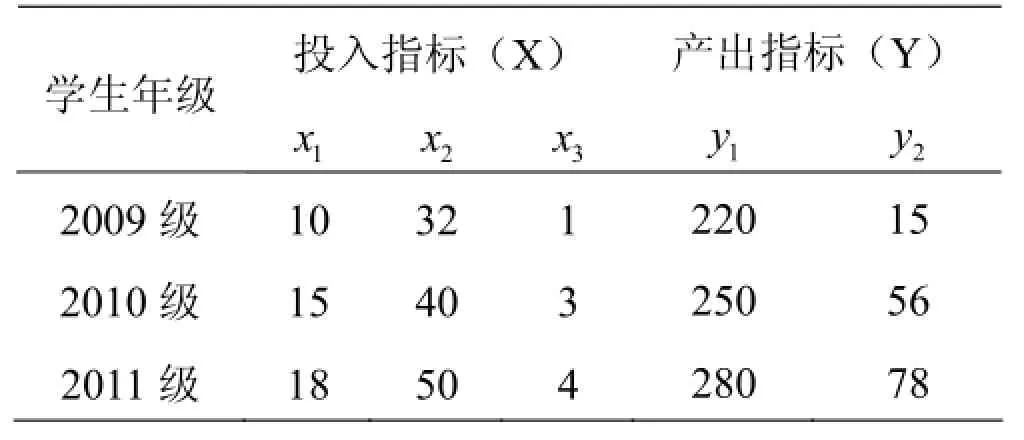
表1　教学投入与产出的数据

模型建立如下：

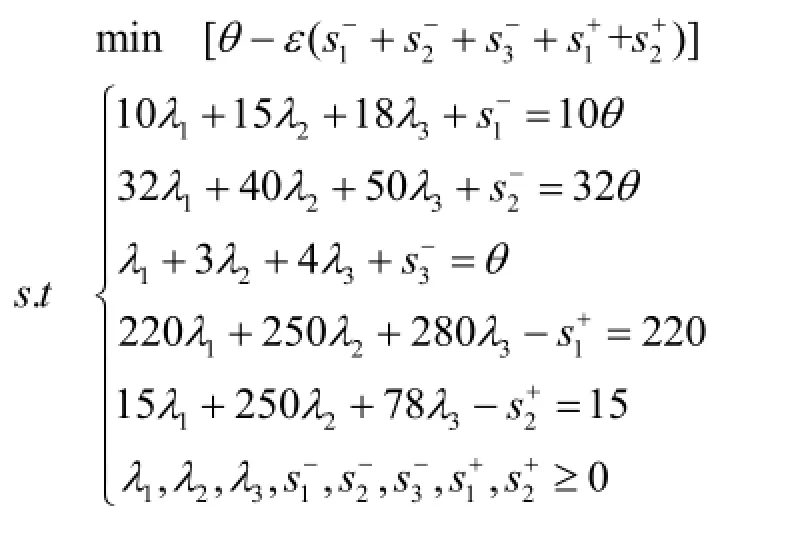
其中，θ 为三个投入量（教育经费、教师人数和图书经费）的效率评价指数，1λ、2λ、3λ为三个投入量的组合比例，S-、S+为松弛变量。

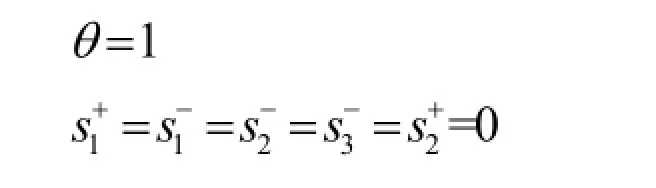
用LINDO软件求解得结果为：由此可知：DMUj为DEA有效。

例 2 农业银行在铜仁市内开设四个新的营业点，投入指标量分别为职员人数、营业点面积和储蓄存取量三个方面，产出指标为贷款量和业务量，具体数据如表 2所示。以一个月为试行时间，建立含非阿基米德无穷小量ε的CCR模型，判断这四个营业点的效率性及可行性。

表2　银行的各投入和产出指标值

模型建立：

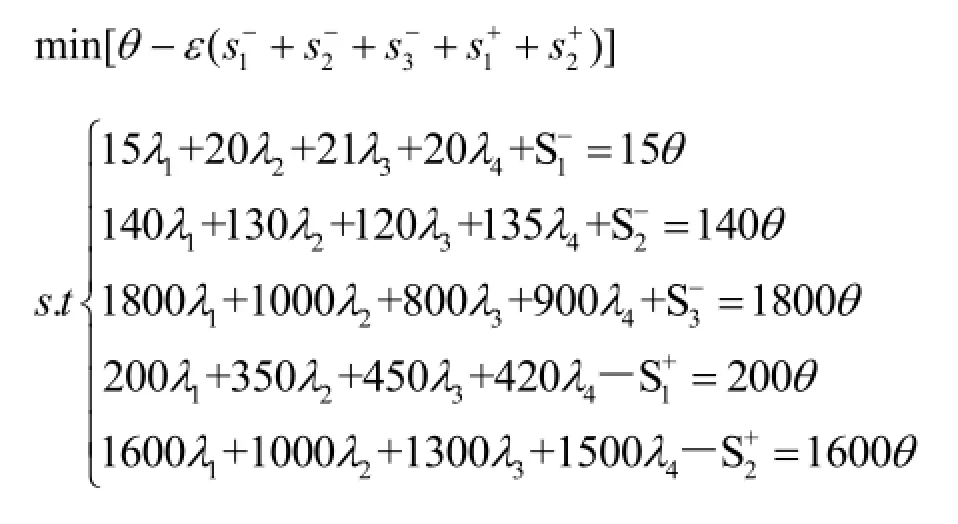
通过LINGO软件得到计算结果如下：

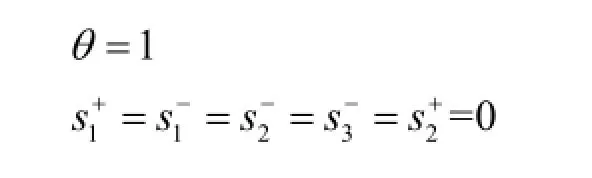
结论：决策单元是DEA有效的。即农业银行建立的 4个营业点在一个月之内是规模收益递增的，银行可考虑继续保留4个营业点。

［1］魏权龄，岳明.DEA概论与CCR模型——数据包络分析［J］.系统工程理论与实践，（1）：58-62.

［2］魏权龄.数据包络分析［M］.北京：科学出版社，2004：1-20.

［3］李光金，刘永清.基于多目标规划的DEA［J］.系统工程理论与实践，1997，（3）：16-22.

［4］马占新.数据包络分析方法的研究进展［J］.系统工程与电子技术，2002，（3）：43-44.

［5］张宝成，王万乐.含非阿基米德无穷小量DEA模型的研究综述［J］.系统工程学报，2010，（3）：407-410.

The Application of the CCR Model Containing Non-Archimedes Dimensionless ε

LI Wei1，YANG Hui2
（1. School of Mathematical Science，Tongren University，Tongren，Guizhou 554300，China；2. School of Science，Guizhou University，Guiyang，Guizhou 550025，China ）

The simplex method of linear programming was mainly used to solve the CCR model which contains non-Archimedes dimensionlessεand judge the DEA efficiency of decision-making units. The paper introduced two applicable examples related to practical life by constructing models and analyzing the software. On the base of the models，LINGO was used to solve the examples and judge whether the decision-making unit is effective.

data envelopment analysis （DEA）；CCR model；multi-objective decision-making

O22；F223

A

1673-9639 （2015） 04-0165-03

（责任编辑 毛志）（责任校对 徐松金）（英文编辑 田兴斌）

2015-03-09

黎薇（1981-），女，贵州铜仁人，讲师，硕士，研究方向：运筹规划、应用数学。