二次直纹曲面的新判别法
2015-10-11熊宗洪
熊宗洪,姚 娟
(贵州民族大学 理学院,贵州 贵阳 550025 )
二次直纹曲面的新判别法
熊宗洪,姚娟
(贵州民族大学 理学院,贵州 贵阳 550025 )
本文先给出二次直纹曲面的判别法则,并利用四类经典二次直纹曲面的某些性质,建立了它们相应的新判别法则。最后,举出若干实例加以应用。
直纹曲面;二次锥面;二次柱面;单叶双曲面;双曲抛物面;直母线;新判别法
在空间解析几何中,二次直纹曲面是一类很重要的曲面,对二次直纹曲面最为经典的判别法是利用不变量和半不变量[1,2]。本文先给出二次直纹曲面的判别法则,再分别利用四类经典二次直纹曲面的某些性质,系统地建立了相应的新判别法则。无疑,这是对空间解析几何该部分内容的一个补充。
1.二次直纹曲面的统一方程及判别法则
所谓直纹曲面是指由一族或几族直母线所生成的曲面。对直纹曲面的研究,首先考虑函数方程,其中
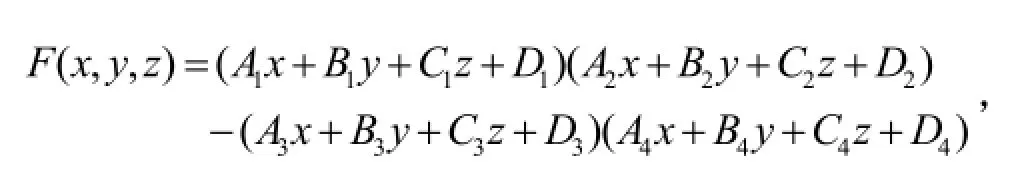
这里Ai、Bi、Ci、Di(i=1,2,3,4)为实数,且A1、B1、C1、A3、B3、C3和A2、B2、C2、A4、B4、C4不同时为零或A1、B1、 C1、 A4、 B4、 C4和A2、B2、C2、A3、B3、C3不同时为零。
判定定理1 设有如上的方程 F(x,y,z)=0,则它的图像为二次直纹曲面S。
证明
将方程 F(x,y,z)=0 改写为

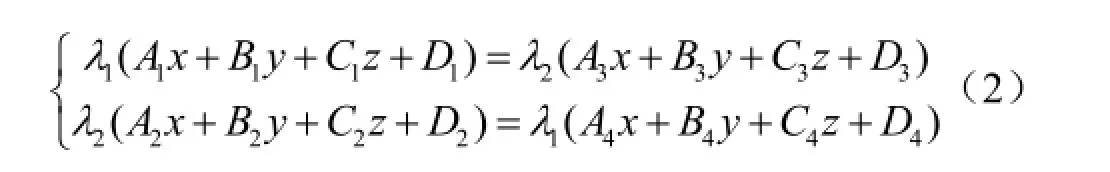
考虑方程组其中1λ、2λ是不同时为零的任意实数。对于12:λ λ的每一比值,方程(2)表示一条直线,称为λ族直(母)线。现在证明,λ族直线可以构成整个曲面S,从而它是曲面S的一族直线。为此需要证明以下两点。
(i)λ族直线中的每一直线在曲面S上。
当120λ λ≠时,将(2)中的两式相乘得到方程(1),这表明当120λ λ≠时,(2)表示的直线在曲面S上。当120λ λ=时,如,则(2)式变为

(ii)在曲面 S上的每一点处,必有直线族(2)中一条直线经过该点。

考虑方程组

这是关于1λ、2λ的二元一次齐次方程组,并由(3)式可知,系数行列式为零。从而上述方程组有非零解,因而可唯一确定比值12:λ λ,于是直线族(2)中有唯一一条直线过0P。
注:(2)表示的直线为λ族直线,也可以将(1)式改为μ族直(母)线:

并且同理可证它也可以构成整个曲面S,从而它也是曲面S的一族直线.
由判定定理1及其证明过程知,无论λ族直线还是μ族直线均可以生成直纹曲面。在此,指出两个概念:若直纹曲面由一族直线生成,称它为 1参数直纹曲面;若直纹曲面由两异族直线生成,称它为2参数直纹曲面。
2.四类直纹曲面的某些性质及新判定法则
现列出空间解析几何教材中直纹曲面的部分性质[3],并通过这些性质给出四类经典直纹曲面的新判定法则。
性质1 柱面和锥面均为1参数直纹曲面,而单叶双曲面和双曲抛物面均为2参数直纹曲面。
性质 2 非平面的锥面和单叶双曲面同族的任意三条两两不同的直母线不平行于同一平面。
性质 3 柱面和双曲抛物面同族的所有直母线都平行于同一平面。
记直纹曲面的同族中任意三条两两不同直母线的方向向量的混合积为Δ,并结合性质 1、2、3给出二次直纹曲面的新判别法则。
判定定理2 (1)设曲面S是1参数直纹曲面,若0Δ=,则S是柱面;若0Δ≠,则S是非平面的锥面。(2)设曲面S是2参数直纹曲面,若0Δ=,则S是双曲抛物面;若0Δ≠,则S是单叶双曲面。
3.实例研究
利用判定定理 1可以将所给二次曲面判别为直纹曲面,再由判定定理 2可以将直纹曲面具体判定为四类经典二次直纹曲面。下面举出若干例子进行说明。
3.1.例1
试问方程

为何种曲面?
解:记所给方程为F(x,y,z)=0,则方程F(x,y,z)=0可以改写为

显然,上式具有本文提及的方程形式,由判定定理1可知,方程 F(x,y,z)=0为直纹曲面。进一步,它的λ族直线和μ族直线分别为

易知,它们为同一方程组,由性质 1可得,F(x,y,z)=0表示的曲面为1参数曲面,从而它或为锥面或为柱面,需要继续判别。为此,取λ族直线的任意三条两两不同的直母线

其方向向量为

综上,F(x,y,z)=0为1参数的直纹曲面且同族直母线中任意三条两两不同直母线的方向向量的混合积为零。由判定定理2可得,F (x,y,z)=0为柱面。
3.2.例2
证明方程

表示锥面。
证明:原方程可以改写为

由判定定理1,方程表示直纹曲面,考虑它的两族族直线

显然,它们为同一方程组。由性质1可知,方程为1 参数曲面。现取λ族直线的任意三条两两不同的直母线

其方向向量为



因L1、L2、L3是三条两两不同的直线,则x、y、z两两不同,从而



当30v=时,30u≠,亦有类似结论。
综上所述,曲面为 1参数的直纹曲面且同族直母线中任意三条两两不同直母线的方向向量的混合积不为零,由判定定理2,方程表示非平面的锥面。
3.3.例3
解:原方程可以改写为

由判定定理 1可知,方程为直纹曲面,考虑它的两族族直线

其方向向量分别为

假设它们共线,则有比例关系


其方向向量为

易计算得3个向量的混合积
于是,该方程为1参数的直纹曲面且同族直母线中任意三条两两不同直母线的方向向量的混合积为零,由判定定理2,曲面为双曲抛物面。
3.4.例4
判别方程

的几何形状.
解:用析因式法将原方程可以改写为

由判定定理1,方程表示直纹曲面,考虑它的两族族直线

其方向向量为
易证得,当1λ、2λ和1μ、2μ都不全为零时,两方向向量不共线。由性质2可得,该直纹曲面是2参数的。考虑λ族直线的任意三条两两不同的直母线

其方向向量为

经过计算和整理可得,这3个向量的混合积

对于0Δ≠的情形,已在例2中讨论。
综上,曲面为 2参数的直纹曲面且同族直母线中任意三条两两不同直母线的方向向量的混合积不为零,由判定定理2可知,曲面为单叶双曲面。
[1]李养成.空间解析几何[M].新版.北京:科学出版社,2010.
[2]吕林根,许子道.空间解析几何[M].第四版.北京:高等教育出版社,2005.
[3]黄宣国.空间解析几何与微分几何[M].上海:复旦大学出版社,2003.
The New Criterion of Quadric Ruled Surfaces
XIONG Zonghong,YAO Juan
(School of Science,Guizhou Minzu University,Guiyang,Guizhou 550025,China )
Firstly,the paper provided judging rule for quadric ruled surfaces. By using some properties of four kinds of classic quadric ruled surfaces,a new criterion was set up. Finally,the paper gave some examples for applying the rules.
ruled surface;quadric cone;quadric cylinder;uniparted hyperboloid;hyperbolic paraboloid;rectilinear generator;new criterion
O182.2
A
1673-9639 (2015) 04-0161-04
(责任编辑 毛志)(责任校对 徐松金)(英文编辑 田兴斌)
2015-05-27
本文系贵州省科技厅联合基金(黔科合LH字[2014]7378),贵州省数学建模及应用创新人才团队项目(黔教科研发[2013]405号)研究成果。
熊宗洪(1982-),男,贵州思南人,讲师,硕士,研究方向:奇点理论。
