基于滑窗置信传播算法的联合信源信道编码

鹿增辉，方 勇，霍迎秋

(西北农林科技大学 信息工程学院，陕西 杨凌 712100)

基于滑窗置信传播算法的联合信源信道编码

鹿增辉，方 勇，霍迎秋

(西北农林科技大学 信息工程学院，陕西 杨凌 712100)

针对联合信源信道编码中信源统计特性和信道噪声参数未知情况下，解码算法性能急剧下降的问题，提出一种基于滑窗置信传播算法(SWBP)的联合信源信道编码，简称滑窗算法。研究采用不规则重复累积(IRA)码来实现基于滑窗置信传播算法的联合信源信道编码，IRA码可以取得与低密度奇偶校验(LDPC)码同样优越的性能，但编码复杂度远远低于LDPC码。在解码端引入滑动窗口，通过实时地估计不断变化的信源统计特性和信道噪声参数，从而提高解码速率。实验结果表明该算法具有接近相关参数已知情况下的理想性能、不依赖于初始参数、复杂度低且易于实现等优点。

联合信源信道编码；不规则重复累积码；置信传播；相关参数估计；低密度奇偶校验码

通信的目的是实现消息从信源到信宿的可靠传输，该过程一般需要进行信源编码和信道编码。信源编码的主要目的是提高码字序列中码元的平均信息量，即去除消息中的冗余，提高传输效率。信道编码的目的在于提高系统的可靠性，通过增加冗余位和校验信息，使系统具有一定的纠错能力和抗干扰能力，从而极大地避免码流传送中误码的发生[1]。在香农信源信道分离理论的指导下，通常信源编码和信道编码分离开来进行独立地编解码[2]。然而，在许多场景下，独立编码已经不能满足实际的需求，例如：受资源限制的系统、时变系统和多用户系统等，因此联合信源信道编码逐渐成为当前的研究热点之一。通常联合信源信道编码有如下几种实现方案：分层编码[3]、基于低密度奇偶校验(Low Density Parity Check， LDPC)码的联合译码[4]、Turbo码[5]和多描述编码[6]。不规则重复累积码(Irregular Repeat Accumulate， IRA)是一种特殊的LDPC码，不仅可以实现对信源的压缩，而且可以进行信道容错，因此本文中采用IRA码来实现联合信源信道编码[7]。

在IRA码译码算法中，对信源统计特性和信道噪声相关参数的估计，仍是影响解码算法性能的重要因素[8]。为了提高解码效率，学者们提出了许多参数估计方法。郑思明等人提出基于粒子滤波的置信传播算法[9]，该方法在标准置信传播算法基础上引入粒子滤波的过程，通过为每个变量节点赋予不同权重的随机粒子，然后在每次标准置信传播译码之后，重新计算粒子的置信和权重，舍弃权重较小的粒子，保留权重大的粒子，以实现对信源后验概率的估计。方勇提出基于滑窗的置信传播(Belief Propagation，BP)算法[10]，该算法的主要思想是在解码端引入滑动窗口，在每轮置信传播算法迭代之后，不断地对信源参数进行估计和更新，从而提高译码算法性能。

鉴于上述研究是基于理想信道进行的缺点，本文在IRA联合译码算法的基础上提出一种改进的IRA联合译码算法，即基于滑窗置信传播算法的联合信源信道编码。改进的IRA联合译码算法基于标准联合译码算法基础上引入滑动窗口，解码的同时对信源似然概率信息和信道噪声似然信息进行实时估计，从而极大地提高解码速率。改进的IRA联合译码算法具有时间复杂度低，对初始值不敏感等优点。

1 基于IRA码的联合信源信道编码

传统的联合信源信道编码，首先使用信源码对信源进行压缩，再串连一个信道码以实现信道容错。本文采用一种特殊的LDPC码，即IRA码。它既可以实现信源压缩，又可以实现信道容错，非常适合联合信源信道编码的应用场景。

1.1 系统模型与描述

如图1所示，利用在解码器中引入一个内嵌编码器的方法可以将分布式编码转化为传统编码[11]，如图1所示。具体转换过程如下：sx=Hx，其中sx为x的伴随式，H为奇偶校验矩阵。在解码端，首先计算边信息y的伴随式sy=Hy，则s=sx⊕sy=H(x⊕y)=Hz。此时，可以将信源x和边信息y之间交叉概率的估计问题转换为求z统计特性参数。

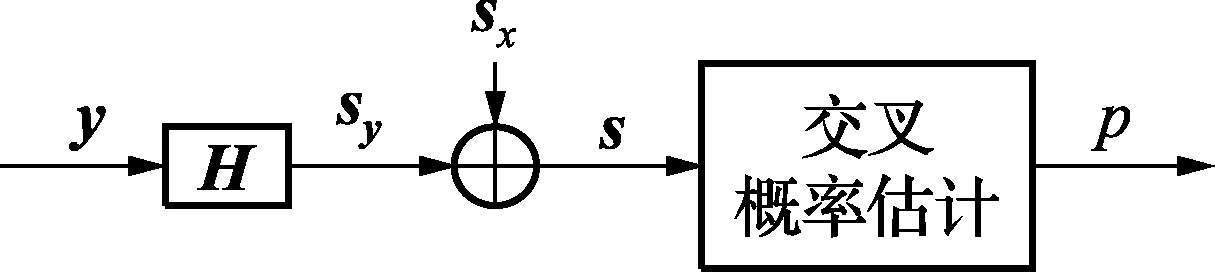
图1 解码器中引入内嵌编码器模型

1.2 基于IRA的编码器和解码器

图2所示为IRA码的二分图表示，IRA码有变量节点和校验节点[12]。[x1,x2,…,xn]和[u1,u2,…,um]代表变量节点，[s1,s2,…,sm]表示校验节点。

图2 IRA码二分图表示

基于IRA码的联合信源信道编码的原理可描述如下[13]：

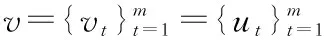
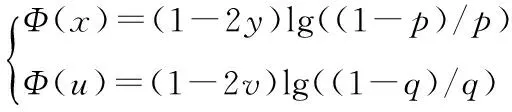
(1)

再通过IRA译码算法进行解码，就可以恢复信源x和u。

上述过程可以总结为：两边的变量节点，将置信度传递给中间校验节点。然后中间的校验节点，再将自身置的信度分别传递给两边的变量节点。此过程不断迭代，直至译码成功或达到最大迭代次数。实际上，x到s的过程为压缩，从s到u是一个容错过程。

2 改进的IRA联合译码算法

在信源统计特性和信道噪声参数未知的情况下，为了解决IRA联合译码算法性能急剧下降的问题，本文基于滑窗置信传播算法提出改进的IRA联合译码算法，以下简称滑窗置信传播算法。下面分别从滑窗置信传播算法的流程、改进后的译码算法和参数估计三方面对改进后的算法进行介绍。

2.1 符号说明

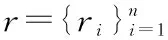
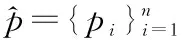
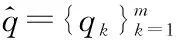
Li：与变量节点xi相连的所有校验节点的索引集合；

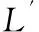
Mj：与校验节点sj相连的变量节点xi的索引集合；

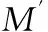
αij：xi传递给sj的消息；

αkj：uk传递给sj的消息；

βji：sj传递给xi的消息；

βjk：sj传递给uk的消息。

2.2 算法流程图

图3 SWBP算法流程图

2.3 IRA联合译码算法

标准的IRA联合译码算法，包含如下4步：

1) 变量节点向校验节点传递消息

(2)

2) 校验节点向变量节点传递消息

(3)

3) 计算后验概率

(4)

4) 硬判决译码

(5)

2.4 参数估计

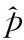
1)信源统计特性的估计

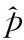
(6)

(7)

2)信道噪声参数的估计

类似于对信源统计特性的估计，对于信道噪声参数的估计，同样使用滑窗技术。估计公式如下

(8)

3 窗口大小的确定

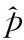
3.1 自适应窗口大小算法描述

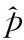
(9)

(10)

则该问题可转化为

(11)

(12)

3.2 搜索策略

在寻找最优窗口大小时，不需要从1到n搜索每个奇数。一方面，窗口太大或太小时该算法的性能都不会太好。另一方面，相邻两个窗口的大小对算法性能影响差别不大。因此，可采取间隔一个距离的方法进行搜索，假设间隔为20，则分别搜索大小为21、41、61等窗口。

4 实验结果

实验采用IRA码仿真滑窗算法的译码性能及其参数估计能力。对实验中的参数做如下说明：假设信源的统计特性取值为正弦函数，即pi=p+(p-0.01)×sin(2πi/n)。假设信道的噪声参数也取值正弦函数，即qk=q+(q-0.01)×sin(2πk/m)。使用码长为6 336的规则码，交叉测试6种不同的速率，即q取值0.05时，p分别取值0.02，0.03，0.04，0.05，0.06，0.07；p取值0.04时，q分别取值0.02，0.03，0.04，0.05，0.06，0.07。

表1描述了码长为6 336的规则IRA码，当q取0.05时，信源统计特性p在6种不同速率下的译码性能。其中ideal列表示在已知非平稳信源的统计特性的条件下，IRA码获得的实际编码速率；static列表示将非平稳信源看成平稳信源，且使用p来初始化变量节点的置信度，获得的实际编码速率；swbp-p列表示在不知道平稳信源的统计特性条件下，使用p来初始化变量节点置信度，运行SWBP算法获得的编码速率。同理swbp-2p、swbp-0.5p列是分别使用2p和0.5p初始化置信度获得的编码速率。

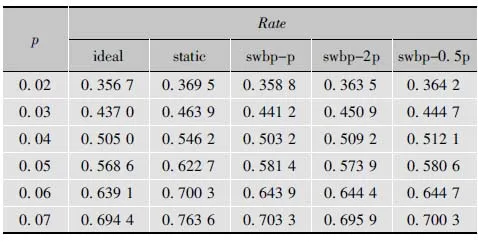
表1 q为0.05时、p在6种不同码率下的译码性能

从表1的实验结果可以看出，在信源统计特性未知的前提下，SWBP算法的性能接近于已知信源统计特性的理论性能，即ideal列与swbp-p列非常接近。主要是因为SWBP算法在迭代译码的过程中不断地对非平稳信源的统计特性和噪音参数进行估计与更新。swbp-p列、swbp-2p列和swbp-0.5p列实验结果非常接近，这说明对于不同初始化参数p、2p和0.5p对SWBP算法影响不大，因此，该算法具有鲁棒性，其性能曲线如图4所示。

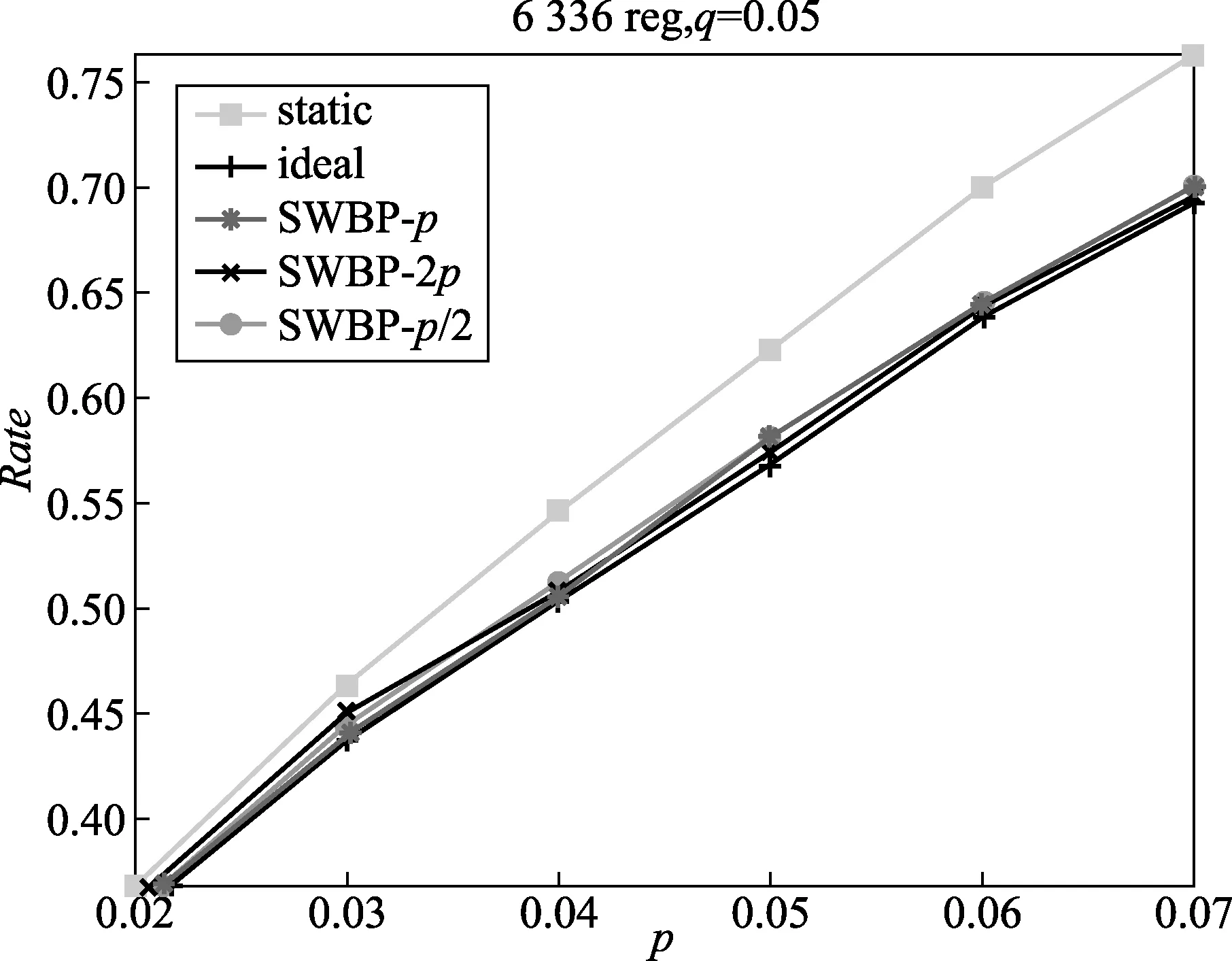
图4 p在6种不同速率下的译码性能

表2描述了码长为6 336的规则IRA码，当p取0.04时，信道噪声参数q在6种不同速率下的译码性能。其中ideal列表示在已知信道噪声参数的条件下，IRA码获得的实际编码速率；static列表示将信道噪声看成平稳变化的，且使用q来初始化置信度，所获得的实际编码速率；swbp-q列表示在未知信道噪声参数条件下，使用q来初始化置信度，运行SWBP算法获得的编码速率。同理swbp-2q、swbp-0.5q列分别表示使用2q和0.5q初始化置信度获得的编码速率。

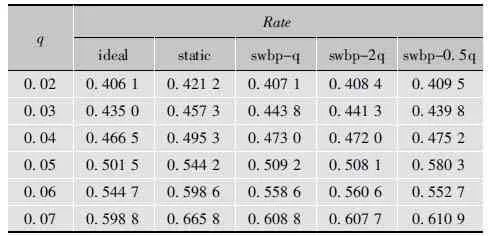
表2 p为0.04时q在6种不同码率下的译码性能

从表2的实验结果可以看出，在信道噪声参数未知的前提下，SWBP算法的性能接近于已知信道噪音参数的理论性能，即ideal列与swbp-q列非常接近。这主要是因为SWBP算法在迭代译码的过程中不仅可以估计信源的统计特性还可以估计信道的噪声参数。swbp-q列、swbp-2q列和swbp-0.5q列实验结果非常接近，这说明SWBP算法对于不同初始化参数q、2q和0.5q不敏感，具有鲁棒性，其性能曲线如图5所示。

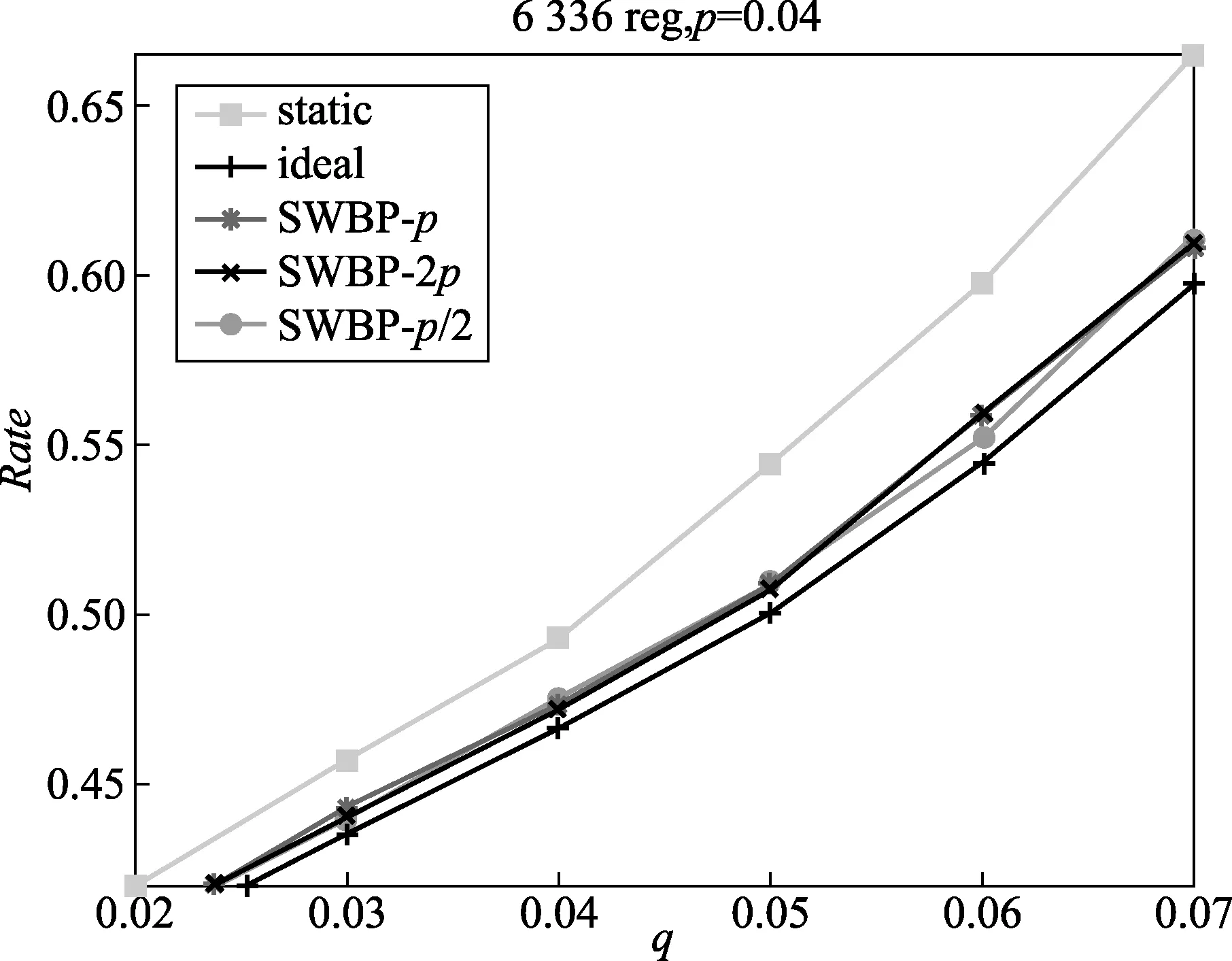
图5 q在6种不同速率下的译码性能

5 结束语

本文提出了一种基于SWBP的联合信源信道编码方法，其主要思想是在译码阶段引入滑窗算法，不断对信源统计特性和信道噪声参数进行估计和更新，从而提高了译码性能。该方法有效地解决了在译码阶段信源统计特性和信道噪声参数未知的情况下，译码性能急剧下降的问题。本实验采用的信源统计特性服从正弦函数，由于滑窗算法对当前变量节点局部统计特性的估计依赖于其周围变量节点的置信度，因此该方法对其他连续非平稳信源同样适用。实验结果表明，该方法的性能接近于理想情况下的性能，具有简单易实现、时间复杂度低和不依赖于初始值等优点。

[1] 陈运. 信息论与编码[M]. 2版.北京：电子工业出版社，2011.

[2] SHANNON C E. A mathematical theory of communication[J]. Bell System Technical Journal，1948(27)：379-423.

[3] 席志红，肖春丽，刘晓慧. 基于ROI图像传输的联合信源信道编码的研究[J]. 应用科技，2008，35(11)：11-14.

[4] 赵旦峰，王诗力，周相超. 基于隐马尔科夫模型的多元LDPC联合译码[J]. 电子科学，2013，26(8)：4-6.

[5] 贾镇泽，马林华，张嵩，等. RS码与LDPC码的联合迭代译码[J].电视技术，2013，37(17)：200-203.

[6] 张丹，李晓峰，简冲，等. 一种多参数优化的联合信源信道编码方法[J].计算机应用研究，2010，27(4)：1530-1533.

[7] 袁基睿，陈贺新，赵岩. 基于H.264和Turbo码的信源信道联合解码[J].吉林大学学报：工学版，2007，37(5)：1187-1191.

[8] 余华，曹维娜，赵力，等. 信源信道联合编码技术用于AVS传输的研究[J]. 电视技术，2007，31(8)：9-10.

[9] XU Q， STANKOVIC V， XIONG Z. Layered Wyner-Ziv video coding for transmission over unreliable channels[J]. Signal Processing，2006，86(11)： 3212-3225.

[10] FANF Yong. Analysis on crossover probability estimation using LDPC syndrome[J]. Science China： Information Sciences，2011，54(9)：1895-1904.

[11] WANG S，CUI L，CHENG S，et al. Noise adaptive LDPC decoding using particle filtering[J]. IEEE Trans. Commun.，2011，59(4)：913-916.

[12] FANG Yong. LDPC-based lossless compression of nonstationary binary sources using sliding-window belief propagation[J]. IEEE Trans. Communications，2012，60(11)：3161-3166.

[13] FANG Yong. Crossover probability estimation using mean-intrinsic- LLR of LDPC syndrome[J]. IEEE Commun. Lett.，2009，13(9)： 679-681.

[14] 周胜源，曹治政，臧岚，等.不规则LDPC码度分布的优化设计研究[J]. 电视技术，2012，36(15)：90-93.

[15] FANG Yong. Joint source-channel estimation using accumulated LDPC syndrome[J]. IEEE Commun. Lett. 2010，14(11)：1044-1046.

鹿增辉(1990— )，硕士生，主研信源信道编码方向的研究；

方 勇(1979— )，教授，博士生导师，主要从事编码理论、网络信息论、图像压缩与传输、并行计算等方向的研究，为本文通讯作者。

责任编辑：时 雯

Joint Source-channel Coding Based on Sliding-window Belief Propagation

LU Zenghui，FANG Yong， HUO Yingqiu

(CollegeofInformationEngineering，NorthwestA&FUniversity，ShaanxiYangling712100，China)

To solve the problem of unknown source statistical properties and channel noise parameters and that of the decoding performance degradation， a new joint source-channel coding scheme based on the Sliding-Window Belief Propagation (SWBP) algorithm is proposed. In this paper， irregular repeat accumulate (IRA) is adopted to achieve the SWBP algorithm in joint source-channel coding. IRA coding can obtain the same superior performance with low density parity check (LDPC) coding， but less than complexity. A sliding-window is introduced in the decoder， and the decoding rate is improved by estimating the changing source statistical properties and channel noise parameters real-timely. The experiment results show that the performance of the proposed algorithm is close to the ideal curve when correlation parameters have been given. While the algorithm shows other advantages， including the robustness to initial parameters， the low linear time complexity， and easy to implement.

joint source-channel coding； irregular repeat accumulate coding； belief propagation； correlation estimation； low density parity check coding

【本文献信息】鹿增辉，方勇，霍迎秋.基于滑窗置信传播算法的联合信源信道编码[J].电视技术,2015，39(11).

国家自然科学基金项目(61271280)；中央高校基本科研业务项目(QN2013086)

TN911.2

A

10.16280/j.videoe.2015.11.023

2015-01-19