Effects of spatial variation in cohesion over the concrete-rock interface on dam sliding stability
2015-10-09AlexandraKrounisFredrikJohanssonStefanLarsson
Alexandra Krounis,Fredrik Johansson,Stefan Larsson
Division of Soil and Rock Mechanics,KTH Royal Institute of Technology,Stockholm,SE-10044,Sweden
Effects of spatial variation in cohesion over the concrete-rock interface on dam sliding stability
Alexandra Krounis*,Fredrik Johansson,Stefan Larsson
Division of Soil and Rock Mechanics,KTH Royal Institute of Technology,Stockholm,SE-10044,Sweden
A R T I C L E I N F O
Article history:
in revised form
20 July 2015
Accepted 3 August 2015
Available online 8 October 2015
Concrete gravity dam
Sliding stability
Cohesion
Brittle failure
Spatial variation
A B S T R A C T
The limit equilibrium method(LEM)is widely used for sliding stability evaluation of concrete gravity dams.Failure is then commonly assumed to occur along the entire sliding surface simultaneously. However,the brittle behaviour of bonded concrete-rock contacts,in combination with the varying stress over the interface,implies that the failure of bonded dam-foundation interfaces occurs progressively.In addition,the spatial variation in cohesion may introduce weak spots where failure can be initiated. Nonetheless,the combined effect of brittle failure and spatial variation in cohesion on the overall shear strength of the interface has not been studied previously.In this paper,numerical analyses are used to investigate the effect of brittle failure in combination with spatial variation in cohesion that is taken into account by random fields with different correlation lengths.The study concludes that a possible existence of weak spots along the interface has to be considered since it significantly reduces the overall shear strength of the interface,and implications for doing so are discussed.
©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by
Elsevier B.V.All rights reserved.
1.Introduction
In Sweden and many other regions/countries of the world,there are an increasing number of older dams in need of safety reassessments to evaluate their compliance with modern safety regulations.One important failure mode considered is sliding. Several techniques for safety assessment with regard to sliding are available,with the traditional limit equilibrium method(LEM)being the most popular,accepted and widely used approach.In LEM, the dam is modelled as a rigid body allowed to slide along its base, and the safety is evaluated by the ratio between the driving forces and the resisting forces.In general,the available shear strength of the dam-foundation contact is expressed by the Mohr-Coulomb failure criterion,and the resisting forces are determined by integrating the normal stresses over the potential sliding plane.The technique is based on the assumption that the shear strength is simultaneously mobilised along the entire sliding surface at the time of failure(Ruggeri et al.,2004).In order for that simplification to be valid,the interface must behave as an elastic-perfectly plastic material.However,tests conducted on concrete-rock cores taken from dams show that an elastic-brittle response is to be expected for cores with bonded interfaces(Rocha,1964;Link,1969;Lo et al., 1990;EPRI,1992).The elastic-brittle response,in combination with the varying stress conditions along the interface,means that a progressive mechanism of failure would be a better description of the interface behaviour.In addition,it is likely that parts with high and low values of cohesion could be expected to appear in clusters with a certain correlation distance.According to Westberg Wilde and Johansson(2013),the reason for this is that the bond strength depends on factors such as the results from cleaning the rock surface prior to the concrete casting,the local rock mass quality and the location of leakage and other degradation processes.Possible spatial variation in cohesion over the interface may introduce weak areas where the failure process can be initiated and contributes further to the uncertainties regarding the failure behaviour of the bonded contact.Since progressive failure can lead to the failure of interfaces which appear to be stable when only the mean value of the peak strength is considered,the simplified Mohr-Coulomb model commonly used in LEM will result in an overestimation of the interface shear resistance and thus dam safety.
Numerical methods,which allow for the incorporation of the deformability of the materials and different sliding and opening criteria for the interfaces,have been implemented for analyses of concrete dams.The constitutive models usually adopted for potential sliding surfaces in the dam body at the dam-foundation interface and in the foundation are of the Mohr-Coulomb type, ruled by the friction angle and cohesion(Foster and Jones,1994;Dawson et al.,1998;Liu et al.,2003;Zhou et al.,2008;Chen and Du, 2011;Jia et al.,2011;Sun et al.,2011).Linear elastic and nonlinear fracture mechanics models,governed by fracture toughness and fracture energy,are also used(Ebeling et al.,1997;Kishen,2005;Saouma,2006).When fracture mechanics models are used,the semi-brittle behaviour of bonded interfaces is taken into account. However,when Mohr-Coulomb type constitutive models are used for the concrete-rock interface,the semi-brittle behaviour of bonded contacts is rarely considered.Dawson et al.(1998)and Jia et al.(2011)constituted the rare exceptions.Yet in none of the cases published has the spatial variation in cohesion been included in the analysis,which means that its impact on the assessed dam safety is still uncertain.There is thus a need to genericallystudyand quantitatively determine the impact of brittle failure in combination with a possible variation in the bond strength on the assessed dam safety.
In this paper,the influence of a brittle material model in combination with spatial variation in cohesion on the assessed sliding stability of a hypothetical dam monolith,with dimensions similar to those of a typical Swedish concrete gravity dam,is investigated using numerical experiments.The reason put forward for using numerical methods is that physical observations of dam failure due to sliding are almost impossible to be realized for economic,technical and environmental reasons.The numerical experiments are performed using the three-dimensional(3D)finite difference programme FLAC3D(Itasca Consulting Group Inc,2011).Mohr-Coulomb constitutive material models are used for the interface to provide a straightforward comparison with the factor of safety(FS)obtained using LEM.The distribution of cohesion is estimated from results of direct tensile tests on concrete-rock cores extracted from a concrete dam located in Sweden,and the spatial variation over the sliding surface is taken into account through the use of random fields.Comparisons are conducted between the numerical results obtained using ductile and brittle material models for the interface and values of FS determined analytically by LEM to analyse the discrepancy between the different models.Finally,there is a discussion on the results and how possible spatial variation in bond strength could be incorporated into re-assessments of existing concrete dams.
2.Factor of safety
In this section,the definition of FS used in this paper is presented.The limit equilibrium and strength reduction techniques, used to determine FS in the analytical and numerical analyses, respectively,are also described.A detailed review of the two methods for use in rock engineering and a comparison between them are provided in Ureel and Momayez(2014).Previous studies, within the fields of geotechnical and rock engineering,where comparisons between FS obtained using LEM and the strength reduction technique are conducted,can be found in Matsui and San(1992),Cala and Flisiak(2001),Cheng et al.(2007),Chen et al.(2014),etc.
2.1.Limit equilibrium method(LEM)
According to LEM,a structure is stable with regard to sliding when,for any potential sliding surface,the resultant shear stress required for equilibrium(τ)is lower than the available shear strength(τF).FS is thus determined as the ratio between these quantities,i.e.FS=τF/τ.
Definingthemaximumshearstrengththatcanbemobilisedusing the Mohr-Coulomb failure criterion,the shear strength available locally for each point of the concrete-rock interface is given by
τF=c+σNtanφ(1)
whereσNis the effective normal stress;and c andφare the cohesion and internal friction angle of the bonded interface,respectively.In order to estimate the shear force of the total interface(TF), it is assumed that the ultimate capacity is simultaneously achieved along the entire sliding surface and the normal stress is integrated over the potential sliding plane.This gives
TF=cA+N′tanφ(2)
where N′is the resultant of the effective forces normal to the assumed sliding plane including the effects of uplift,and A is the area of the sliding surface.By also integrating the resultant shear stresses over the sliding plane,the global FS against sliding at the concrete-rock interface,FSLEM,can be determined according to

where H is the resultant of the horizontal loads acting on the structure.
2.2.Strength reduction technique
There are two common techniques to determine failure due to sliding using numerical techniques:reducing the shear strength of the interface until failure occurs,or increasing the applied loads until failure occurs.Since increasing the load could lead to other types of failures,e.g.overturning,which are not considered in this paper,the shear strength reduction technique(SRT)is applied here.SRT is a popular technique when numerical modelling for stability analyses of rock and soil slopes is used and was employed as early as 1975by Zienkiewicz et al.(1975). In the field of dam engineering,the technique has been applied by Alonso et al.(1996),Liu et al.(2003),Zhou et al.(2008),Chen and Du(2011),and Jia et al.(2011)among others.In this study, the technique is implemented using the 3D explicit finite difference code FLAC3D.FLAC3Dand the two-dimensional(2D)code FLAC have been widely used for numerical stability evaluations of rock slopes(Sjöberg,1999a,b;Latha and Garaga,2010)and soil slopes(Zettler et al.,1999;Dawson and Roth,1999),and have also been applied in stability analyses of concrete dams by Kieffer and Goodman(1999),Bu(2001),Léger and Javanmardi(2006),Gustafsson et al.(2010),and Yang et al.(2012)among others.
The analysis is initially carried out with the actual load and resistance parameters of the structure studied to establish the initial stress conditions.After this,the resistance parameters of the interface,φand c,are simultaneously and progressively decreased by a factor RF according to Eqs.(4)and(5)while keeping the applied load conditions unchanged.The computation continues until failure occurs.

cRF=c/RF(5)
The interface strength just prior to failure can be considered as the shear strength required for equilibrium.It then follows,from the definition of FS in Section 2.1,that the numerical FSSRTcan be determined according to

where RFeqis the reduction factor at the limit bearing capacity state.
3.Method for numerical analyses
3.1.Modelling procedure
Three stages of numerical analyses are performed(Fig.1).The main purpose of the first stage is to check the accuracy of the result obtained by LEM compared to the numerical solution, where stresses and strains are included in the analysis.The interfaceistherefore assumed tofollowtherequirements imposed by plastic-perfectly failure theory(Fig.2).This is achieved by using the default constitutive model provided in FLAC3D, defined by the linear Coulomb shear strength criterion and governed byφ,c,dilation angle(ψ),normal stiffness(Kn)and shear stiffness(Ks)of the interface.
In the second stage of the numerical analyses,the effect of brittle failure is studied.The elastic-brittle-plastic or strainsoftening models(Fig.2)are commonly adopted to simulate brittle rock failure(Hajiabdolmajid et al.,2002),a mechanism of the same type as the brittle concrete-rock interface failure.In this study,the elastic-brittle-plastic model is implemented for the interface,and the peak shear strength is described by the Mohr-Coulomb failure criterion.In order to reproduce the behaviour described,the“bond”model available in FLAC3Dis used.The logic of the“bond”model means that the interface remains elastic before the bond strength and that the bond breaks if either theshear stress exceeds the shear strength or the tensile normal stress exceeds the normal strength of the interface.The“bond”model is managed by the tension,representing the normal bond strength,and the sb ratio,i.e.the ratio between the shear and normal bond strengths. Because of the normal stress distribution and,in the following stages,the spatial variation in c over the interface,the shear and tensile strengths of the different interface elements vary.The builtin programming language FISH is therefore used to calculate the tensile strength of each element(σt,i)according toσt,i=ci/2 based on Griffith's failure criterion(Griffith,1921).FISH is also used to estimate the sb ratio assigned to each element according to sbi=τp,i/σt,i,whereτp,iis calculated using Eq.(1).The computation then proceeds in the same way as described for the previous stage.

Fig.2.Schematic representations of the post-peak responses of various material models.
In stages 1 and 2,the concrete-rock interface is assumed to be homogeneous with regard to c,i.e.a single value,equal to the sample mean of c,is assigned to all interface elements.In order to analyse the effect of a possible spatial variation in c on the peak shear strength,a third stage of calculations is performed.The“bond”model is used to represent the interface behaviour,and the analysis is performed in the same way as described for stage 2. However,a random field is used in order to represent the fluctuation of c from point to point.Each point of the interface is thus assigned a different value of c,randomly chosen from a predefined distribution function for the parameter.Since the location of elements with high or low values of c in relation tothe normal stresses along the interface may affect the initiation and propagation of failure,stage 3 is carried out for several different realisations of random fields generated from the same distribution function.The more the realisations implemented,the greater the confidence that can be placed in the estimated magnitude of the error. Nevertheless,due to extensive computational time,the number of realisations is limited to 10.

Fig.1.Schematic of the analyses outline.
3.2.Definition of failure
When numerical methods are used for stability analyses,failure is commonly determined based on either the obtained deformations or the occurrence of divergence.In the present study,the occurrence of a divergence(a simulation is considered to have converged when the normalised unbalanced force of every node in the mesh is less than 10-5within 200,000 iterations)is regarded as the loss of the static-force equilibrium state and is taken as the failure condition.The reason is that the technique where failure is defined based on the inflection point of the deformation curve is more susceptible for human errors.However,since the choice of 200,000 as the iteration ceiling is subjective(it can be mentioned that at a balanced state,the number of iterations required to reach stable conditions,once the shear strength properties have been reduced by 0.1,varies between approximately 35,000 at early stages to 150,000 just prior to failure),bonding conditions and deformations at the interface of the dam are also checked in order to verify the results obtained.
3.3.Limitations
One limitation associated with the methodology used is the simultaneous reduction of all strength parameters,both peak and residual.Once the peak shear strength of an interface element is reached,the residual shear strength of the node has been reduced to a lower value than the initial residual shear strength of the element.This means that the stress redistribution may not be entirely representative of the real stress redistribution and that higher stresses than that in reality may be assigned to nearby elements and cause them to yield.
It should also be mentioned that,for most real dams,it is reasonable to assume that the concrete-rock interface is partially bonded(Lo et al.,1990).Yet,in this paper,the entire area under the dam monolith is assumed to be bonded,which may deviate from real conditions.
4.Application to dam monolith
4.1.Input
4.1.1.Geometry and mesh
An outline of the hypothetical dam body used in the analyses is shown in Fig.3.The dam monolith is 30 m high and 8 m wide.The dimensions of the dam monolith are based on the geometry of typical Swedish concrete dams and were chosen so that the entire base of the monolith will be under compression.The numerical model of the dam also includes part of the foundation,45 m in depth,101 m in length and 8 m in width.The dam and foundation are modelled using solid elements,while the dam-foundation contact is modelled using specific interface elements.Each interface element has a size of 0.1 m×0.1 m in order to be representative of the measurement data,i.e.drilled core size,to minimise possible scale effects and transformation errors in the determination of the material properties.The mesh adopted in the analyses is shown in Fig.4.
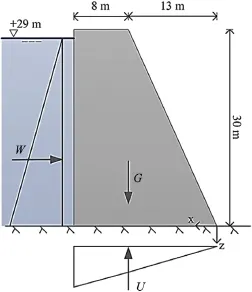
Fig.3.Illustration of the dam monolith geometry.The dam monolith is 8 m wide.
4.1.2.Loads and boundary conditions
A fixed displacement constraint is applied to the bottom boundary while normal displacement constraints are applied tothe side boundaries of the foundation.Only one load case,with the water level at the retention level,is considered.The loads included in the analyses are a horizontal water load acting on the upstream face of the dam monolith(W),uplift(U)and deadweight of the concrete monolith(G).In FLAC3D,W and U are applied as external pressures to the upstream face of the dam monolith and the full area of the base of the dam,respectively.The uplift pressure is assumed to vary linearly from a hydrostatic pressure based on the retention level at the upstream face to zero pressure at the downstream face,while W varies linearly from a hydrostatic pressure based on the retention water at the bottom of the reservoir to zero pressure at the water surface.The relation G=Vcγc, where Vcis the volume of the monolith andγcis the unit weight of the concrete,is used to determine G.
The concrete elastic modulus(Ec),Poisson's ratio(νc),and the unit weight(γc)are set to 30 GPa,0.2,and 24 kN/m3,respectively. The dam monolith is assumed to be located on a strong rock foundation.The rock elastic modulus(Er),Poisson's ratio(νr),and the unit weight(γr)are set to 50 GPa,0.2,and 26 kN/m3, respectively.
The internal friction angle of the bonded concrete-rock interface(φi)is assumed to be equal to that reported by EPRI(1992), φi,peak=54°.Based on the results presented by Lo et al.(1990),the residual friction angle is set toφi,residual=45°.
A population mean ofμc=1.44 MPa and a population variance ofare estimated for c of the bonded interface from the results of direct tensile tests on four bonded cores extracted from a concrete gravity dam located in northern Sweden.Although based on a small number of tests,the results seem reasonable compared to those presented by EPRI(1992).A lognormal distribution is chosen to avoid unrealistic negative values.
In stages 1 and 2,c is assumed to be equal toμc.In stage 3,the distribution function of c is used to generate the random fields utilized.A measure to describe the degree of spatial correlation of c is also necessary to generate the fields.Such a measure is the correlation length,also called the scale of fluctuation(e.g.Vanmarcke, 2010).Unfortunately,the magnitude of the correlation length of cohesion(θc)at existing dams is generally unknown.Therefore,two different correlation distances,θc=0 m andθc=10 m,are assumed for comparison.The correlation lengths are taken to be statistically isotropic.
Realisations of the cohesion fields are made in the computer software R!(Hornik,2006)using the Random Fields package(Schlater,2001)that simulates Gaussian random fields.Since c is assumed to follow a lognormal distribution,the first step in the realisation procedure is to determine the mean value(μlnc)and variance)of lnc based on the relationship between the normal and lognormal randomvariables.Then random fields are generated for lnc and transformed back into c according to c=elnc.Fig.5a shows a realisation of a random field with correlation length of 0 m where high values of cohesion are randomly mixed with lower values.A realisation of a random field with correlation length of 10 m is shown in Fig.5b.

Fig.4.Finite difference mesh adopted in the study.

Fig.5.Realisation of c with(a)θc=0 m and(b)θc=10 m.
The empirical relationproposed by Barton and Choubey(1977)is used to determine the initial value of Ks:

whereτfis the peak shear strength,and L is the critical joint length. However,sinceτFof the concrete-rock interface is not homogeneous,Kscannot be defined by a single value.Eq.(4)is therefore applied separately to each element along the interface in the numerical analyses.This is done by first deciding an initial value for the entire interface based on the mean values of c andφi,where the estimated averageof the interface,based on the assumption of equal loading conditions,is obtained by dividing the sum of all vertical forces(G and U)by the total area of the interface.The estimated initial value is then used as input in the numerical analysis where the stress conditions over the interface are estimated.Once the initial stress distribution over the interface has been calculated,Ksof each element is updated based on c and the calculated value offor the specific element.This is an iterative process,repeatedforeverystep,whichmaycausestress redistribution along the interface.The initial value is set to Ks=0.19 MPa/mm based on L=1 m andσ′N=0.35 MPa.Since Eq.(4)is based on the behaviour of rock joints,the reasonableness of the estimated value of Ksis checked by comparing it with the results presented by Saiang et al.(2005)for shotcrete-trachyte and shotcrete-magnetite cores.For the currentrangeof normal stresses, the estimated initial value of Ksis within the limits of the values presented by Saiang et al.(2005).
The normal stiffness to shear stiffness ratio R=Kn/Ksis used to determine Kn.In this paper,a ratio of 10,which lies within the interval of values presented by Bandis et al.(1983),is assumed,and this leads to an initial value of Kn=1.92 MPa/mm.
4.2.Results
For the monolith studied,FSLEM=9.6 is obtained.According to the normal stress distribution at the concrete-rock interface, determined using Navier's formula,the entire base of the dam is under compression so there is no need to update the uplift pressure due to a potential tensile crack at the heel of the dam.
In order for the dam monolith to reach failure in stage 1,the initial shear strength parameters of the interface are reduced by a factor of 10.4 under current loading conditions.Thus,the factors of safety against sliding obtained using LEM and SRT with a homogeneous interface and a ductile constitutive model for the interface agree reasonably well,with FSSRTbeing slightly higher than FSLEM. The numerical results also show that,under normal loading conditions and initial shear strength values,the dam monolith is stable with regard to all relevant failure modes,i.e.sliding,overturning and crushing of the foundation or concrete,and the entire base of the dam is under compression,in agreement with the analytical calculations.
In stage 2,when the brittle material model is used to describe the failure behaviour of the homogeneous interface,a somewhat lower value of FSSRT=8.1,which supports the previous findings that numerical models incorporating the FLAC“bond”model cast lower safety factors than LEM models for gravity dams(Altarejos-Garcia et al.,2012),is obtained.The reason for this is that due to the brittle material model,the post-peak load that an element of the interface can carry is lower than the estimated peak shear strength.Thus,once the peak shear strength of an interface element is exceeded,the stresses around the element will increase. This may cause nearby points to yield,resulting in further stressredistributions and so the process continues in a consecutive manner until the surface of failure extends to the point where kinematic release becomes possible as shown in previous studies of dam stability(Bolzon,2010;Jia et al.,2011).A comparison between FSLEMand FSSRTobtained in stage 2 shows that for a homogeneous interface,the assumption of ductile failure results,for the analysed monolith,in an overestimation of FSLEMby approximately 20%.
FSSRTvalues calculated in stage 3,when the spatial variation in cohesion over the interface is included in the analyses,together with FSLEMfor each realisation are given in Tables 1 and 2 for θc=0 m andθc=10 m,respectively.The deviations between FSLEM and FSSRTfor each realisation,representative of the error associated with Eq.(4),are also presented.Whenθc=0 m,the deviation between FSLEMand FSSRTvaries between 46.8%and 66.1%,with an average of 56.7%and standard deviation of 5.9%.Whenθc=10 m is assumed for cohesion,the deviation between FSLEMand FSSRTvaries between 41.4%and 58.2%,with an average of 52%and standard deviation of 5%.
In Fig.6,the deviations between FSLEMand FSSRTare plotted againstμc,randomfieldfor each realisation.The deviation between FSLEMand FSSRTobtained in stage 2 is also shown in the figure.It can be seen that no overall trend can be detected for the different cases. The deviations obtained whenθc=0 m followa linear trend,where the deviation increases with the mean value of c.This is due to FSSRTbeing nearly constant for all realisations(Table 1)while FSLEMis correlated toμc,randomfield.Whenθc=10 m is assumed,the deviations calculated exhibit a more random scatter.From the values presented in Table 2,it seems that,although FSSRTin general increases with the mean value of c,the degree of correlation is slightly lower than that for FSLEM,which results in the pattern shown in Fig.6.
In Fig.7 the debonding of the concrete-rock interface due to decreased shear strength is plotted against RF for stage 2 and two typical cases of stage 3.It can be seen here that,for a homogeneous interface,the debonding process initiates at the upstream part of the interface,whereσNis at its lowest,for RF close to RFeqand then almost immediately propagates to the rest of the interface.When the spatial variation in c is taken into account,the debonding process is initiated much earlier.Furthermore,from the start,the debonding is scattered over the entire interface.Nonetheless,when θc=0 m is assumed,the debonding is completely randomly distributed;while forθc=10 m,a pattern where nearby elements debond at the same time can be detected.This indicates that the location and size of the clusters of elements with related values of c have an impact on the failure process of the interface,which could explain the somewhat lower degree of association between FSSRTandμc,randomfieldthan that between FSLEMandμc,randomfield, resulting in the scatter observed in Fig.6.

Table 1 A summary of the mean values of c for random fields,used as input in the numerical analyses in stage 3,the corresponding FSLEMand FSSRTand the deviations between FSLEMand FSSRTfor realisations withθc=0 m.
To check the reasonableness of the obtained results,the deformation of the monolith was also controlled for the different stages. Fig.8 shows typical deformation curves.It can be seen from the figure that the obtained deformations just prior to failure are approximately 1.5 mm.These deformations are on the high end of the range measured and presented by Saiang et al.(2005),for laboratory samples with bonded interfaces.However,since they represented the deformation of a dam monolith with significantly larger dimensions than regular laboratory test samples,they are deemedas reasonable.It can also be seen that,asexpected,defining failure based on deformations generates a somewhat lower FSSRTthan that when the convergence criterion is used.Nevertheless,the discrepancy is nearly negligible and the obtained values of FSSRTare therefore considered acceptable.

Table 2 A summary of the mean values of c for random fields,used as input in the numerical analyses in stage 3,the corresponding FSLEMand FSSRTand the deviations between FSLEMand FSSRTfor realisations withθc=10 m.
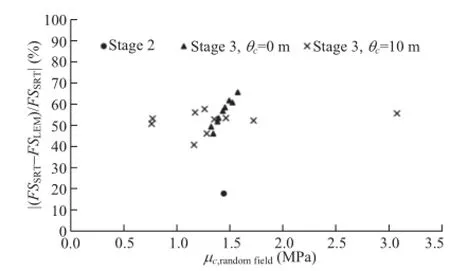
Fig.6.Deviations between FSLEMand FSSRTplotted against the mean value of interface cohesion for each realisation.
5.Discussion
5.1.Application example
The results fromthe numerical analyses show that the analytical LEM,commonly used in dam stability analyses,results in an overestimation of the assessed dam stability with regard to sliding.The results also indicate that spatial variation in c along the interface results in weak spots where failure can be initiated,in contrast to a homogeneous interface where failure is initiated at the location with lowest normal stress,and further diminishs the validity of the ductile model,leading to an overestimation of the factor of safety with regard to sliding by approximately 40%-65%.From the spread of the results presented in Section 3.2,both within and between different cases,it is evident that,for the monolith studied,the uncertainty associated with Eq.(4)cannot be represented by one constant value unless the exact composition of the interface is known.
Although the results presented in this paper are only valid for the specific dam monolith under the stated boundary conditions,it is reasonable to believe that a possible spatial variation in c mayalso have a significant influence on the behaviour of other damfoundation systems with bonded or partly bonded concrete-rock interfaces.It follows that a reliable framework for incorporating the uncertainties associated with the erroneous assumptions of ductile failure in combination with spatial variation in cohesion is required in order to avoid an overestimation of the sliding stability of gravity dams with bonded concrete-rock interfaces.

Fig.7.Debonding of the contact area due to gradual shear strength reduction.Slip now marks the elements that have debonded during the current step of the numerical analysis, slipped in past marks elements that have debonded during previous steps with lower RF,and no slip marks elements where the bond is still intact.R4 and R5 mean realisations 4 and 5,respectively.
5.2.Incorporation of spatial variation in c in sliding stability analyses of existing dams
A majority of the national regulations/guidelines for dam safety assessment and reassessment available today are based on deterministic techniques and uncertainties are generally dealt with by using target safety factors.However,in the Swedish guidelines(SwedEnergy,2012),uncertainties related to the shear strength of bonded contacts are regarded as so significant that cohesion is disregarded when sliding stabilityassessments of existing dams are performed.This approach is on the safe side but may lead to expensive and unnecessary strengthening of dams.An alternative approach for dealing with the greater uncertainties associated with cohesion is to apply separate,higher partial safety factors to cohesion than to the frictional component.According to Ruggeri et al.(2004),this technique has been adopted in the Spanish,Portuguese,Chinese,Indian,French,and Swiss regulations.In other regulations/guidelines,where a single global FS is used,it is instead common to refer to higher target values for FS when the effect of cohesion is included in the overall shear strength of the interface than that when only frictional strength is considered(FERC,2002;CDA,2007).Nonetheless,it is unclear to what extent the higher reduction factors applied to the cohesion component and the higher target values of global FS reflect the errorassociated with theapplied model for the shear strength since they are mainly determined based on experience and not on actual knowledge about the impact of the model error on the assessed safety of the dam. Furthermore,the uncertainty associated with the design values of the shear strength properties,arising not only from the natural variation of the parameters but also from the scarce amount of data upon which they are commonly determined,has also to be taken into account by the same FS.It is thus questionable whether a uniform level of safety can be achieved by using a single,constant value of FS without regard to the degree of uncertainty involved in the calculation.

Fig.8.Horizontal displacements vs.reduction factor for typical cases.
A more robust framework for incorporating uncertainties in the analyses is provided in probability-based methods such as structural reliability analysis.Such methods have not been used extensively in dam safety assessments;however,in recent years,interest in using probability-based approaches for dam safety assessment and reassessment has increased.Probability-based approaches have been taken into account in various regulations or guidelines(ANCOLD,2003;Hartford and Baecher,2004;ICOLD,2005;USBR, 2011;SPANCOLD,2013).Moreover,one of the main themes at the 11th ICOLD Benchmark Workshop on Numerical Analysis of Dams dealt with estimation of the probability of failure of a gravity dam for the sliding failure mode(ICOLD,2011).A review of published papers in which probabilistic analysis of the sliding failure mode is performed,including de Araújo and Awruch(1998),Ellingwood and Tekie(2001),Saouma(2006),Altarejos et al.(2009),Lupoi and Callari(2010,2012),ICOLD(2011),and Westberg Wilde and Johansson(2013),showed that the cohesion/adhesion of the concrete-rock interface is commonly included in the evaluation of the peak shear strength without taking the progressive failure mechanism into consideration.The only exceptions in the aforementioned publications were Saouma(2006)and Westberg Wilde and Johansson(2013),who included the progressive failure mechanism of bonded interfaces in their analyses.Saouma(2006), however,did not include the effect of a possible spatial variation in cohesion,while Westberg Wilde and Johansson(2013)did not take into account the initial stress distribution,the stress redistributions or the stiffness of the interface.
Nonetheless,probability-based methods are subjected to the same uncertainty regarding the degree to which the applied model mimics reality as the traditional deterministic LEM.Thus, for probability-based methods to be considered,a reliable option for sliding reassessment of dams with bonded concrete-rock interfaces,accurate modelling of the uncertainty associated with progressive failure is required.JCSS(2001),among others,suggested that deviations between real behaviour and the behaviour predicted by the model can be dealt with by introducing a random variable representative of the uncertainty associated with a specific model.The numerical experiments presented in this paper can be used as a starting point for quantifying such a random variable representative of the uncertainty associated with the brittle material model in combination with spatial variation in c.
6.Concluding remarks
Based on the results presented in this paper,it can be concluded that it is not enough to only consider the brittle material model and model cohesion with a deterministic value;the influence of potential weak spots along the interface has to be taken into account since it further reduces the overall shear strength of the interface significantly.
It can also be concluded that,if simple analytical methods such as LEM are to be used fordam safety assessment and reassessment, further research is required to determine whether the target values of FS commonly used today are representative of the uncertainty related to the interface properties and the simplified model used for defining the shear strength of bonded concreterock interfaces.
The limit state function commonly used in most probabilitybased methods is based on the same failure model as that used in analytical deterministic analyses.Probability-based methods are thus also subjected tothe same uncertainties as LEM is.Therefore,a reliable and preferably simple methodology for including this particular uncertainty needs to be developed.The numerical experiments presented herein can be used as a starting point for such a methodology.
Conflict of interest
The authors wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.
Acknowledgements
The research presented was carried out as a part of“Swedish Hydropower Centre-SVC”.SVC has been established by the Swedish Energy Agency,Elforsk and Svenska Kraftnät together with Luleå University of Technology,KTH Royal Institute of Technology,Chalmers University of Technology and Uppsala University. The authors also wish to acknowledge Diego Mas Ivar at Itasca Consultants AB for offering invaluable advice concerning FLAC3Dthat greatly assisted the research,although any errors and the interpretations/conclusions of this paper are those of the authors.
References
Alonso E,Carol I,Delahaye C,Gens A,Prat P.Evaluation of safety factors in discontinuous rock.International Journal of Rock Mechanics and Mining Sciences&Geomechanics Abstracts 1996;33(5):513-37.
Altarejos L,Escuder I,de Membrillera MG,Serrano A.Risk analysis and probability of failure of a gravity dam.In:Proceedings of the 23rd International Congress on Large Dams.Brasilia:International Commission on Large Dams(ICOLD);2009.
Altarejos-GarciaL,Escuder-BuenoI,Serrano-LombilloIA,deMembrillera-Ortuño MG.Methodology for estimating the probability of failure by sliding in concrete gravity dams in the context of risk analysis.Structural Safety 2012;36-37:1-13.
Australian National Committee on Large Dams Incorporated(ANCOLD).Guidelines on risk assessment.Hobart:ANCOLD;2003.
Bandis SC,Lumsden AC,Barton NR.Fundamentals of rock joint deformation.International Journal of Rock Mechanics and Mining Sciences&Geomechanics Abstracts 1983;20(6):249-68.
Barton N,Choubey V.The shear strength of rock joints in theory and practice.Rock Mechanics 1977;10(1):1-54.
Bolzon G.Collapse mechanisms at the foundation interface of geometrically similar concrete gravity dams.Engineering Structures 2010;32(5):1304-11.
Bu S.Seismic evaluation of concrete gravity dams using FLAC.In:Bilaux D,Rachez X, Detournay C,Hart R,editors.FLAC and numerical modeling in geomechanics. Rotterdam:A.A.Balkema;2001.p.39-46.
Cala M,Flisiak J.Slope stability analysis with FLAC and limit equilibrium methods. In:Bilaux D,Rachez X,Detournay C,Hart R,editors.FLAC and numerical modeling in geomechanics.Rotterdam:A.A.Balkema;2001.p.111-4.
Canadian Dam Association(CDA).Dam safety guidelines-technical bulletin 9. Structural consideration for dam safety.CDA;2007.
Chen DH,Du CB.Application of strength reduction method to dynamic anti-sliding stability analysis of high gravity dam with complex dam foundation.Water Science and Engineering 2011;4(2):212-24.
Chen J,Liu J,Xue J,Shi Z.Failure analyses of a reinforced embankment by strength reduction and limit equilibrium methods considering hardening of soft clay. KSCE Journal of Civil Engineering 2014;18(7):2043-50.
Cheng YM,Lansivaara T,Wei WB.Two-dimensional slope stability analysis by limit equilibrium and strength reductions methods.Computers and Geotechnics 2007;34(3):137-50.
Dawson EM,Roth WH.Slope stability analysis with FLAC.In:Detournay C,Hart R, editors.Proceedings of the International Symposium on FlAC and Numerical Modeling in Geomechanics.Rotterdam/Brookfield:A.A.Balkema;1999.p.3-9.
Dawson RV,Curtis DD,Donnelly RC.Sliding resistance of concrete gravity dams. CEA No.9331 G 2002.Canadian Electricity Association Technologies Inc.(CEATI);1998.
de Araújo JM,Awruch AM.Probabilistic finite element analysis of concrete gravity dams.Advances in Engineering Software 1998;29(2):97-104.
Ebeling RM,Pace ME,Morrison EE.Evaluating the stability of existing massive concrete gravity structures founded on rock.Technical Report REMR-CS-54.US Army Corps of Engineers(USACE);1997.
Electric Power Research Institute(EPRI).Final Report.Report EPRI TR-100345.Uplift pressures,shear strengths and tensile strengths for stability analysis of concrete gravity dams,vol.1.Denver,CO:Stone and Webster Engineering Corporation;1992.
Ellingwood B,Tekie PB.Fragility analysis of concrete gravity dams.Journal of Infrastructure Systems 2001;7(2):41-8.
Federal Energy Regulatory Commission(FERC).Engineering guidelines for the evaluation of hydropower projects,Chapter III:gravity dams.Washington DC:US Department of Homeland Security Federal Emergency Management;2002.
Foster J,Jones HW.Procedure for static analysis of gravity dams including foundation effects using the finite element method-Phase 1B.Technical Report ITL-94-5.US Army Corps of Engineers(USACE);1994.
Griffith AA.The phenomena of rupture and flow in solids.Philosophical Transactions of the Royal Society A:Mathematical Physical and Engineering Sciences 1921;221:163-98.
Gustafsson A,Johansson F,Löwen KE,Stille H.Analysis,instrumentation and upgrading of the Krokströmmen arch dam.In:Proceedings of the 8th ICOLD European Club Symposium,Dam Safety:Sustainability in a Changing Environment.Innsbruck;2010.
Hajiabdolmajid V,Kaiser PK,Martin CD.Modelling brittle failure of rock.International Journal of Rock Mechanics and Mining Sciences 2002;39(6):731-41.
Hartford D,Baecher G.Risk and uncertainty in dam safety.London:Thomas Telford Publishing;2004.
Hornik.The R FAQ.2006.http://cran.r-project.org.
ICOLD.Risk assessment in dam safety management-a reconnaissance of benefits, methods and current applications.Bulletin 130.Paris:ICOLD/CIGB;2005.
ICOLD.Theme C-estimation of the probability of failure of a gravity dam for the sliding failure mode.In:Proc.11th International Benchmark Workshop on Numerical Analysis of Dams.Valencia:ICOLD;2011.
Itasca Consulting Group Inc.FLAC3D-fast lagrangian analysis of continua in three dimensions,Version 4.0.Minneapolis,MN:Itasca Consulting Group Inc.;2011.
Jia C,Gao F,Li Y.Progressive failure research on foundation surface of concrete gravity dams.Advanced Materials Research 2011;163-167:1038-43.
Joint Committee on Structural Safety(JCSS).Probabilistic model code.2001.http:// www.jcss.byg.dtu.dk/Publications/Probabilistic_Model_Code.aspx.
Kieffer DS,Goodman RE.Evaluating an old gravity dam on a soft foundation using FLAC.In:Detournay C,Hart R,editors.Proceedings of the International FLAC Symposium on FlAC and Numerical Modeling in Geomechanics.Rotterdam/ Brookfield:A.A.Balkema;1999.p.33-7.
Kishen CJM.Recent developments is safety assessment of concrete gravity dams. Current Science 2005;89(4):650-6.
Latha GM,Garaga A.Seismic stability analysis of a Himalayan rock slope.Rock Mechanics and Rock Engineering 2010;43(6):831-43.
Léger P,Javanmardi F.Structural stability of concrete gravity dams strengthened by rockfill buttressing:hydrostatic load.Journal of Geotechnical and Geoenvironmental Engineering 2006;132(12):1591-9.
Link H.The sliding stability of dams,part III.International Water Power and Dam Construction 1969;21(5):172-9.
Liu J,Feng XT,Ding XL.Stability assessment of the three gorges dam foundation, China using physical and numerical modeling-Part II:numerical modeling.International Journal of Rock Mechanics and Mining Sciences 2003;40(5):633-52.
Lo KY,Lukajic B,Wang S,Ogawa T,Tsui KK.Evaluation of strength parameters of concrete-rock interface for dam safety assessment.In:Proceedings of Canadian Dam Safety Conference.Toronto;1990.p.71-94.
Lupoi A,Callari C.A probabilistic method for the seismic assessment of existing concrete gravity dams.Structure and Infrastructure Engineering:Maintenance, Management,Life-Cycle Design and Performance 2012;8(10):985-98.
Lupoi A,Callari C.Probabilistic seismic assessment of concrete dams.In:Furuta H, Frangopol DM,Shinozuka M,editors.Safety,reliability and risk of structures, infrastructures and engineering systems.London:Taylor&Francis Group;2010. p.1758-65.
Matsui T,San KC.Finite element slope stability analysis by shear strength reduction technique.Soils and Foundations 1992;32(1):59-70.
Rocha M.Mechanical behavior of rock foundations in concrete dams.In:Transactions of the 8th International Congress on large dams.Edinburg;1964.
Ruggeri G,Pellegrini R,Rubin de Celix M,Berntsen M,Royet P,Bettzieche V, Amberg W,Gustafsson A,Morison T,Zenz G.Sliding stability of existing gravity dams-final report.ICOLD European Club;2004.
Saiang D,Malmgren L,Nordlund E.Laboratory tests on shotcrete-rock joints in direct shear,tension and compression.Rock Mechanics and Rock Engineering 2005;38(4):275-97.
Saouma V.Reliability based nonlinear fracture mechanics analysis of concrete dam -a simplified approach.Dam Engineering 2006;16(3):219-41.
Schlater M.Simulation of stationary and isotropic random fields.R-News 2001;1(2):18-20.
Sjöberg J.Analysis of failure mechanics in high rock slopes.In:Vouille G,Berest P, editors.Proceedings of the 9th ISRM International Congress,Paris;1999. p.127-30.
Sjöberg J.Analysis of the Aznalcollar pit slope failures-a case study.In:Detournay C,Hart R,editors.Proceedings of the International FLAC Symposium on FLAC and Numerical Modeling in Geomechanics.Rotterdam/Brookfield:A.A. Balkema;1999b.p.63-70.
Spanish National Committee on Large Dams(SPANCOLD).Technical guide on operation of dams and reservoirs.Vol.1.Risk analysis applied to management of dam safety.SPANCOLD/CNEGP;2013.
Sun GH,Zheng H,Liu DF.A three-dimensional procedure for evaluating the stability of gravity dams against deep slide in the foundation.International Journal of Rock Mechanics and Mining Sciences 2011;48(3):421-6.
SwedEnergy.Kraftföretagens riktlinjer för dammsäkerhet.SwedEnergy;2012(in Swedish).
Ureel S,Momayez M.An investigation of the limit equilibrium method and numerical modeling for rock slope stability analyis.In:Zhang L,Wong ELNY,editors.Rock mechanics and its applications in civil,mining,and petroleum engineering.Reston,VA:American Society of Civil Engineers;2014.p.218-27(CD-ROM).
US Bureau of Reclamation(USBR).Dam safety public protection guidelines(interim).Denver,CO:US Department of the Interior,Dam Safety Office;2011.
Vanmarcke E.Random fields:analysis and synthesis.Hackensack,USA:World Scientific Publishing;2010.
Westberg Wilde M,Johansson F.System reliability of concrete dams with respect to foundation stability:application to a spillway.Journal of Geotechnical and Geoenvironmental Engineering 2013;139(2):308-19.
Yang X,Yang G,Yu T.Comparison of strength reduction method for slope stability analysis based on ABAQUS FEM and FLAC3DFDM.Applied Mechanics and Materials 2012;170-173:918-22.
Zettler AH,Poisel R,Roth W,Preh A.Slope stability analysis based on the shear reduction technique in 3D.In:Detournay C,Hart R,editors.Proceedings of the International FLAC Symposium on FlAC and Numerical Modeling in Geomechanics.Rotterdam/Brookfield:A.A.Balkema;1999.p.11-6.
Zhou W,Chang X,Zhou C,Liu X.Failure analysis of high-concrete gravity dam based on strength reverse factor method.Computers and Geotechnics 2008;35(4):627-36.
Zienkiewicz OC,Humpheson C,Lewis RW.Associated and non-associated viscoplasticity and plasticity in soil mechanics.Géotechnique 1975;25(4):671-89.
18 May 2015
*Corresponding author.Tel.:+46 87908060.
E-mail address:alexandra.krounis@byv.kth.se(A.Krounis).
Peer review under responsibility of Institute of Rock and Soil Mechanics, Chinese Academy of Sciences.
1674-7755©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.
http://dx.doi.org/10.1016/j.jrmge.2015.08.005
杂志排行
Journal of Rock Mechanics and Geotechnical Engineering的其它文章
- Characterizing the influence of stress-induced microcracks on the laboratory strength and fracture development in brittle rocks using a finite-discrete element method-micro discrete fracture network FDEM-μDFN approach
- Effects of fracture distribution and length scale on the equivalent continuum elastic compliance of fractured rock masses
- Shear strength behavior of geotextile/geomembrane interfaces Belén M.Bacasa,*,Jorge Cañizalb,Heinz Konietzkyc
- Engineering properties for high kitchen waste content municipal solid waste
- Evaluation of the effect of sodium silicate addition to mine backfill, Gelfill-Part 2:Effects of mixing time and curing temperature
- Studies on the key parameters in segmental lining design
