基于空间点模式分析的地震空间分布集中趋势特性

郑文锋，李晓璐，顾行发，LAM Nina，刘 珊，谢建军

(1. 电子科技大学自动化工程学院 成都 611731；2..路易斯安那州立大学 美国 路易斯安那 巴吞鲁日 70803；3. 中国科学院遥感与数字地球研究所 北京 海淀区 100101)

基于空间点模式分析的地震空间分布集中趋势特性

郑文锋1,2，李晓璐1,2，顾行发1,3，LAM Nina2，刘 珊1,2，谢建军1

(1. 电子科技大学自动化工程学院 成都 611731；2..路易斯安那州立大学 美国 路易斯安那 巴吞鲁日 70803；3. 中国科学院遥感与数字地球研究所 北京 海淀区 100101)

地震序列的时空相关性在地震运动趋势分析中发挥着基础性的作用。时空相关性的一个最直接作用是一个强震发生以后促使一定空间区域甚至全球范围的地震群的发生。该文借助现有空间点模式分析方法，通过均数中心，加权均数中心，几何均数中心和调和均数中心函数，尝试探索一种空间相关性方法来描述强震与其震后临近的非强震之间的相关性与趋势特性。该文研究工作中，相关性和趋势特性的物理基础是在地理学第一定律的背景下讨论的——任何事物之间时空相关。均数中心函数方法应用于中国境内地区。结果显示，中国境内强震震后的余震群并非以强震为均数中心均匀分布，其均数中心与强震空间位置存在明显偏移特征。

集中趋势; 地震; 地震空间分布趋势; 空间点模式分析; 空间统计

根据地理学第一定律，任何事物都相关，时空距离相近的事物关联更紧密可知，空间距离近的地震联系紧密。目前地震间相关性多通过地表理化表征或从地震成因机理的角度进行研究，如应力与形变、气体效应、地球系统动力学等。本文通过点模式空间分析统计方法，从另一视角描述、解释并预测空间规律特性。

文献[1]通过描点法推测病例“点”分布规律，成功地控制了霍乱；借鉴犯罪学中犯罪事件的二维描述方法，系统地提出了空间分析中描述集中趋势的统计指标，并应用到血吸虫病案例分析中。文献[2]首次提出空间点模式分析的统计理论。文献[3]提出了空间统计的3个分类标准：点模式分析、格网或区域分析和地统计学建模。文献[4]发展了文献[3]的工作。而后，文献[5]将空间点模式分析方法应用到如传染病学等领域。文献[6]分析比较了点集的质心空间分析方法，为地震点集群的中心点分析提供了理论基础。文献[7]提出了一种震中空间的统计分析方法，分析可能存在的断层。文献[8]利用地理统计原理，研究地震点模型分析方法。文献[9]用时空点模式分析方法验证汶川余震的时空集群特征。

本文分析地震点描述性统计特征，取国家尺度的试验区域，以相邻两强震为时间节点，研究各节点后余震的空间分布特性及其与节点间相关性。对1970—2011年间地震数据进行了空间点集群分类和空间分布统计分析，在此基础上探讨地震发生和传播的空间分布规律，及震间相关性分析的方法，为深入挖掘地震点信息奠定基础。

1 时空点模式分析基本原理

空间点模式是基于随机过程理论的空间点过程的一种实现形式[10]，它由所有感兴趣研究事件的空间位置组成，其统计分析多基于事件间的空间距离进行[2,11]。以地震震中点空间位置为研究对象，后文点集群的质心可视为多个点集的“代表”，故由强震与续震质心间的空间位置关系，可体现两者空间方位相关性。质心的涵义较多[12]，本文采用较通用的4种均数定义。

1.1 均数中心

均数中心[6,8]为：

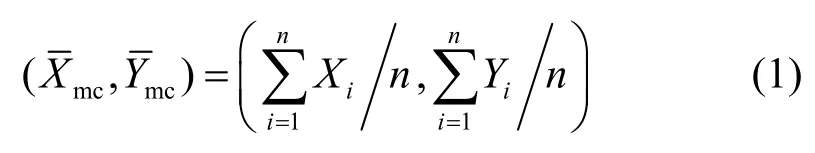
1.2 加权均数中心

通过附加要素Wi，加权均数中心为：

1.3 几何均数中心

空间分析中几何均数中心定义为[1]：

1.4 调和均数中心

空间分析中调和均数中心定义为[1]：

式中，是调和均数中心坐标；其余参数同式(1)。它同样对极端值有一定稳健性，不过对为0或接近0的坐标值情况较脆弱[19]。加权调和均数中心亦不再赘述。

2 中国境内地震分布数据点模式分析

本文假设在中国境内两两地震相关，相关程度正比于两者间空间距离。本文在时间序列上分析众多非强震点集群与和其最临近强震间的相关性。

图1 基础数据叠加效果图

目前，强震没有统一定义，本文强震是震级(Ms)在震级阈值及以上的地震。相关数据均可从相关权威部门或机构获得，收集1970—2011年间地震点数据，经筛选、标准化，建立原始数据Excel统计表，在Arcgis10中生成空间分析数据库，经过配准叠加结果如图1所示。由图可见，地震点和断裂带的分布相当吻合。在时间方向上，以先后发生的两次强震分别作为起点和终点，将各起点同其后下一起点间的所有余震归为一类，进行划分。分别定义震级阈值(Ms)为7及6.5(与强震相对的为非强震)，如图2、图3所示。

图2 中国境内强震空间分布(Ms=7为阈值)

由图2和图3可见，中国境内的强震主要分布于西南地区，分布较为均匀。对比各图可知7级以上强震的分布，更能体现整体分布趋势，而6.5级以上强震分布，将地震点分布的不确定因素反映得更为清晰，有利于对区域状态的分析。

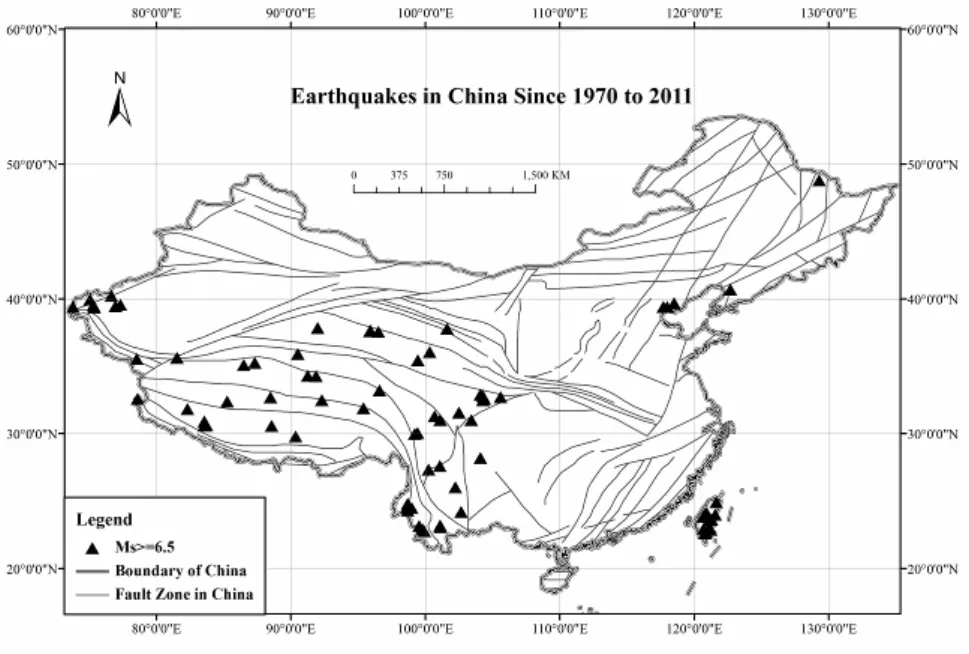
图3 中国境内强震空间分布(Ms=6.5为阈值)

2.1 各类均数中心分析结果分布

中心点计算采用第1.1～1.4节定义进行，加权计算均以震级为权重。约80%的各均数中心落入椭圆框区域，如图4和图5所示，显示出地震点空间分布集中特性。随震级阈值减小，类别数目增多，各均数中心点数目也越多，聚集特性也越明显，但范围稍大。从空间分布方位来看，各中心点大多分布在羌塘地块、松潘-甘孜地块、鲜水河断裂带区域及其附近，各强震点分布较中心点分散。在两类定义中，以震级7为阈值，各中心点的分布最为集中，整体趋势特性最突出。

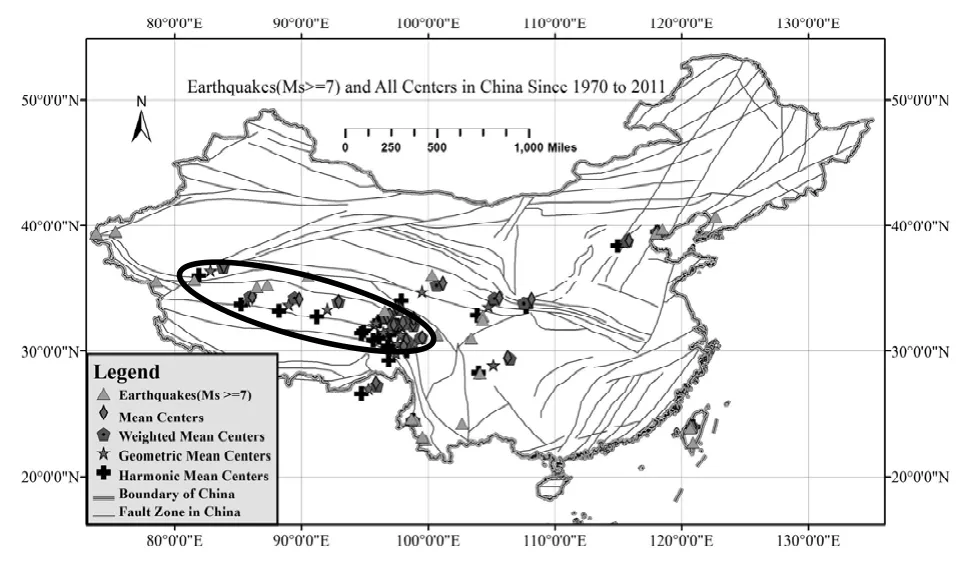
图4 各均数中心与强震(Ms≥7)空间分布

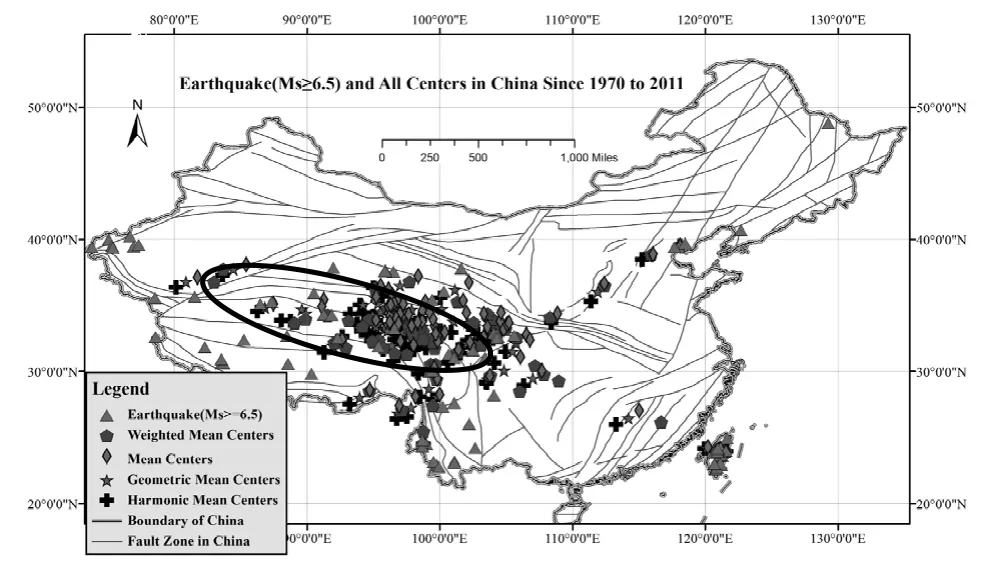
图5 各均数中心与强震(Ms≥6.5)空间分布

2.2 均数中心分析结果分布

将以上各种均数中心对应的强震点和中心连线，可更清楚直观地显示强震与非强震均数中心间的相关性。各非强震系列均数中心分布如图6、图7所示。

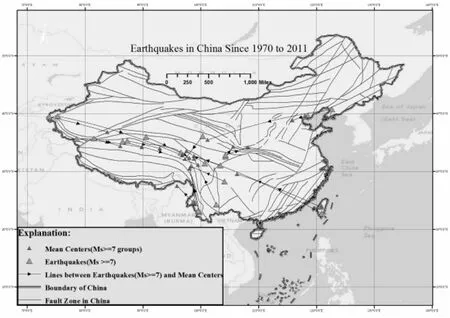
图6 强震与均数中心空间分布(Ms=7为震级阈值)

Ms≥7及6.5的强震点由大三角形点代表，小三角形为非强震点分布均数中心。强震点和对应均数中心的连线是基于椭球体所生成的由强震震中到各均数中心直线，强震以及对应非强震均数中心有一定的相关性，但强震及对应的均数中心点基本不重合。

图7 强震与均数中心空间分布(Ms=6.5为震级阈值)

由图可见，每个强震点以及该震级的一系列非强震的均数中心之间存在着明显的对应关系；同时，强震点分布较均数中心分散；此外，90%以上均数中心点相对于对应强震点，有向鲜水河断裂带中部区域方向偏移的现象——即呈现一定的方向规律，且其偏移规律性随着均数中心点数目增多而更加明显。空间点及连线的分布呈现出轴对称趋势。

综上可知，强震与余震间必然相关而不是独立的，地震点的空间分布也呈现一定规律而不是随机的。故此本文提出一种大胆的猜想：地震震中的空间位置在大约东南至西北方向上呈现震荡的趋势。

2.3 加权均数中心分析结果分布

图8、图9的产生过程与2.2节相似。由图8可见，与各强震对应的均数中心相比，加权均数中心更集中于鲜水河断裂带及其附近。加权均数中心的偏移，显示出鲜水河断裂带附近区域发生震级较大的余震概率偏高。

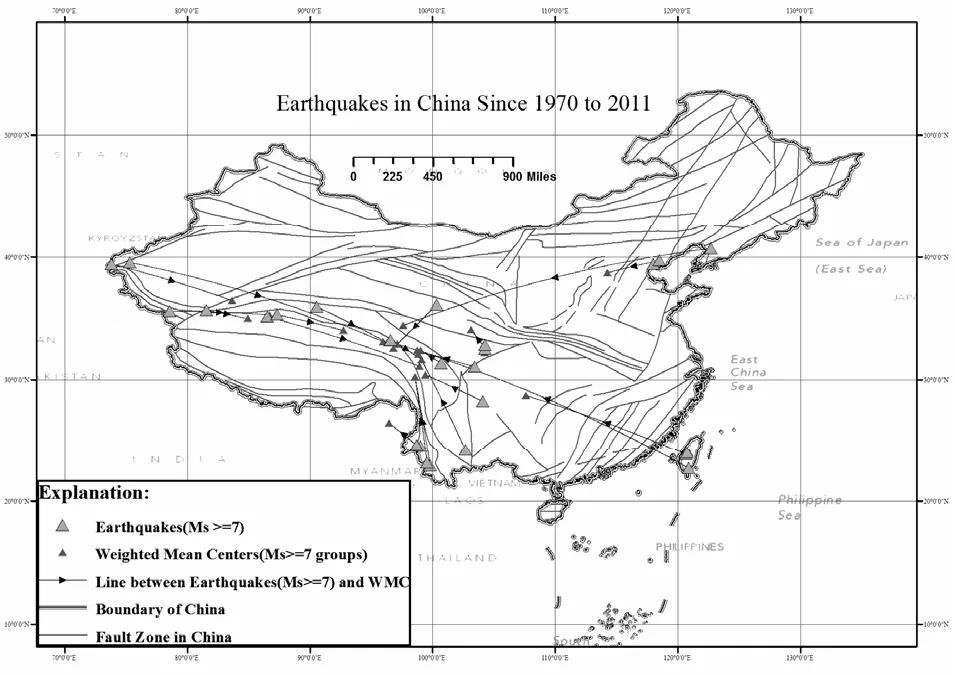
图8 强震与加权均数中心空间分布(Ms=7为震级阈值)

图9中加权均数中心点数目较图7更多，加权均数中心所表现出的特性更为明显。其在图9中龙门山断裂带附近区域也开始显示出相对聚集特性。

图9 强震与加权均数中心空间分布(Ms=6.5为震级阈值)

2.4 几何均数中心和调和均数中心分析结果分布

应用1.3节和1.4节的定义可计算几何均数中心、调和均数中心。图10、图11所示的几何均数中心点集也在前述类别中心聚集区域内呈现出聚集特性。但不同的是，几何均数中心向正南方向有一定的纬度减少，主要原因是在均数中心以北的中国地区，所发生的非强震相对于以南地区稀疏。

图10 强震与几何均数中心空间分布(Ms=7为震级阈值)

图11 强震与几何均数中心空间分布(Ms=6.5为震级阈值)

图12 强震与调和均数中心空间分布(Ms=7为震级阈值)

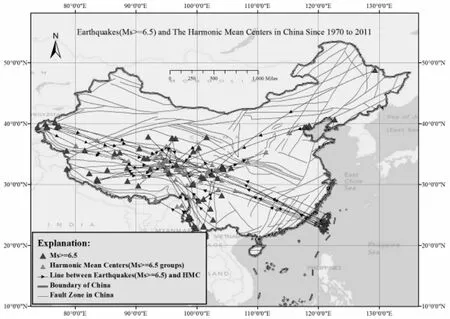
图13 强震与调和均数中心空间分布(Ms=6.5为震级阈值)

由图12知，调和均数中心与几何均数中心空间分布特征大体相同，但前者较后者有一定的纬度减少，前者是本文的四类均数中心，点空间位置纬度最少的一类。从图10～图13知，非强震的几类中心与对应强震间的空间分布，都显示出了较强的相关性，且其聚集特性与前文相似，但较之有不同程度的加强，这表现为点集更为聚集。表明从各空间方位往鲜水河断裂带中部区域方向，有发震频率增加的趋势。

3 讨 论

1979—2011年试验区域累计7级以上强震25例，6.5级以上强震79例。本文中，对于划分点集的震级阈值，分别采用了7和6.5两种标准。从图2、图3知，阈值越小，类别数目越多，各类别点集包括的地震点越少，其信息越个性化，节点对子点集的影响也愈明显，尤其是强震发生较为频繁时，因此也增加了不确定性，对于地震点间的相关性研究更为有利；反之亦然。图4和图5中，各中心点大多分布在羌塘地块、松潘−甘孜地块、鲜水河断裂带区域及附近，而各强震分布较各中心点分散，这可能与该区域的复杂地质构造有关。

图6、图7中，90%以上均数中心相对于强震点，呈现出方向上的偏移规律性。点及连线的空间分布，呈现出轴对称趋势。

由图8和图9知，非强震的加权均数中心与对应的强震之间的分布显示出明显相关性，较均数中心更集中，表明从各空间方位向鲜水河断裂带中部区域方向，有震级增大的趋势；以震级为权重，为0或缺失震级的有效地震点数据将被丢弃，会产生一定的误差。

由图10～图13知，几何均数中心和调和均数中心较均数中心、加权均数中心，向正南方向有一定的纬度减少，可能是因为在均数中心以北的中国地区所发生的非强震，相对于以南地区稀疏。调和均数中心点是本文四类均数中心中，点空间位置纬度最少的一类。从上文可见，中国境内西南地区为强震分布概率较大的区域，其次为北纬40°东经120°附近及台湾半岛周围，而与强震相关的各系列非强震也形成以此区域为中心的分布格局。从整体来看，川滇构造带处于地震多发区中心，发震地点以其为中心向外分散，其分布位置随各方位地质构造环境不同而异。另外，90%左右的强震对应的均数中心，有向鲜水河断裂带中部区域方向偏移的现象，并以强震和地质环境的具体情形而异。从地质构造应力角度来说，龙门山断裂带、鲜水河断裂带是受到印度洋板块与欧亚板块间的应力挤压形成的，属于地震活动是国内最为活跃的地区，而大多强震对于这一区域都会带来一定范围内的余震。也就是说，每次周围区域的强震都会通过震动、应力传递和相互作用，进而促进这一区域的应力释放。

由图7～图13可见，强震−各均数中心−下一次强震间，有强震−非强震−强震的震荡传播效应。这种效应在震级阈值较小时更明显。另外，南天山带地区强震的发生，引发以川滇构造带为中心的非强震，继而由一系列非强震的陆续产生传递触发中国台湾地区的强震。由于川滇构造带的地质构造复杂，此区域的非强震又易诱发该区域的强震，而该区域的强震同样也可以引发本区域一系列非强震。

4 结 论

集中趋势特性对于初步的空间分布分析是非常有帮助的，能为更深层次的研究奠定基础。本文借鉴空间点模式的构建思路和空间各均数中心的空间分析方法，系统研究了地震空间分布的集中趋势。当然，空间分析中描述集中趋势的指标还有很多，每种方法的应用和效果各有特点，各均数中心方法亦然[20]。藉此，本文论述了松潘甘孜构造带−龙门山构造带之间区域的地震分布特殊性，验证了该区域是地震分布较为集中的区域，其发震有概率加大、震级加强的趋势。由此提出这样的推断：松潘甘孜构造带−龙门山构造带之间的区域是中国境内地震发生的核心区域，区域间发震相关性正相关于其空间距离。此外，根据统计分析结果，对地震发生规律的总结提出如下猜想：试验区域强震，通过触发川滇构造带区域的一系列地震(包括强震和非强震)，传递到以川滇构造带为原点的强震点对立方位；试验中强震呈现震荡的传递效应。因为地震发生情形复杂，研究中对很多因素做了简化处理。如考虑到强震和非强震之间相互作用的复杂性，研究初期只考虑了强震与其后临近的非强震间的关系；地震点集是以7和6.5级震级地震的时序特征来划分的，将地震点数据形成“树”状结构，每个非强震都是单一强震的子节点，而非实际的“网”状结构，存在很多局限性。后期将基于现有的研究成果，更全面地对地震的特殊性进行研究。地震成因机理复杂，结合空间分析和统计方法，从空间立体的角度，对地震现象有一个更新的认识。

[1] ZHANG Zhi-jie, PENG Wen-xiang, ZHOU Yi-biao, et al. Study and application on the statistical indices to describe central tendency for spatial analysis[J]. Chinese Journal of Health Statistics, 2008, 25(3): 269-272.

[2] RIPLEY B D. The second-order analysis of stationary point processes[J]. Journal of Applied Probability, 1976, 13(2): 255-266.

[3] CRESSIE N. Statistics for spatial data[M]. New York: Wiley Interscience, 1993.

[4] ANSELIN L. Issues in the specification and interpretation of spatial regression models[J]. Agricultural Economics, 2002, 27(3): 247-267.

[5] DIGGLE P J. Statistical analysis of spatial point patterns[J]. International Journal of Geographical Information Science, 2004, 18(1): 105-106.

[6] MICHAEL J S, MICHAEL F G, PAUL A L. Geospatial gnalysis: a comprehensive guide to principle, techniques and software tools[M]. 2nd ed. Beijing: Publishing House of Electronics Industry, 2007.

[7] AMORESE D, LAGARDE J L, LAVILLE E. A point pattern analysis of the distribution of earthquakes in normandy[J]. Bull Seism Soc Am, 1999, 89(3): 742-749.

[8] ZIMERAS S. Exploratory point pattern analysis for modeling earthquake data[C]//Proceedings of the 1st WSEAS International Conference on Environmental and Geological Science and Engineering (Eg'08): Environment and Geoscience. Malta: [s.n.], 2008: 112-120.

[9] SHI Pei-jian, LIU Jie, YANG Zhen. Spatio-temporal point pattern analysis on Wenchuan strong earthquake[J]. Earthquake Science, 2009, 22(3): 231-237.

[10] MAO Zheng-yuan. The study of extracting structure information of a clustered spatial point pattern[J]. Acta Geodaeticaet Cartographica Sinica, 2007, 37(2): 181-186.

[11] TOBLER W A. Computer movie simulating urban growth in the detroit region[J]. Economic Geography, 1970, 46(2): 234-240.

[12] WOO G. Kernel estimation methods for seismic hazard area source modeling[J]. Bulletin of the Seismological Society of America, 1996, 86(2): 353-362.

[13] MORE H, HALVORSEN K B. The Bayesian bridge between simple and universal kriging[J]. Mathematical Geology, 1989, 21(7): 767-786.

[14] SHURYGIN A M. Statistical analysis and long-term prediction of seismicity for linear zones[J]. Mathematical Geology, 1992, 25(7): 759-772.

[15] SHCHERBAKOV R, TURCOTTE D L, RUNDLE J B. Aftershock statistics[J]. Pure and Applied Geophysics, 2005, 162(6-7): 1051-1076.

[16] LEE J, WONG D W S. Statistical analysis with arcview GIS[M]. New York: John Wiley Sons, Inc, 2001.

[17] CRESSIE N A C. Statistics for spatial data[M]. New York: John Wiley Sons, Inc, 1991.

[18] ELLIOTT P, WAKEFIELD J C, BEST N G, et al. Spatial epidemiology: Methods and applications[M]. New York: Oxford University Press, 2000.

[19] MONMONIER M. Mapping it out[M]. Chicago: University of Chicago Press, 1993.

[20] SENETA E, PARSHALL K H, JONGMANS F. Nineteenth-century developments in geometric probability [J]. Archive for History of Exact Sciences, 2001, 55(6): 501-524.

编辑漆 蓉

Study of the Central Tendency of Earthquake Based on Spatial Point Pattern Analysis

ZHENG Wen-feng1,2, LI Xiao-lu1,2, GU Xing-fa1,3, LAM Nina2, LIU Shan1,2, and XIE Jian-jun1
(1. School of Automation Engineering, University of Electronic Science and Technology of China Chengdu 611731; 2. Louisiana State University Baton Rouge LA USA 70803; 3. Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences Haidian Beijing 100101)

Correlations in space and time among approaching earthquakes play a fundamental role in earthquake motion trend analysis. One direct effect of the correlations is a promotion of earthquake swarms occurred in a certain region even worldwide after a strong earthquake. The variability of the random variable over space in correlations may occur in earthquake swarms after strong earthquakes. Using the classical analysis method of spatial point pattern, it is possible to introduce a measure of spatial correlation and trend between strong earthquakes and the aftershocks, through the function of mean center (MC), weighted mean center (WMC), geometric mean center (GMC) and harmonic mean center (HMC). The method of mean center functions is applied to the earthquakes of China. The result shows that in China, aftershock swarms did not evenly spread around the strong earthquakes as the mean center. And there is an obvious migration between the strong earthquakes and the mean centers position of aftershock swarms.

central tendency; earthquake; earthquake spatial trend; spatial point pattern analysis; spatial statistics

TP315

A doi:10.3969/j.issn.1001-0548.2015.04.015

2013 − 07 − 03；

2015 − 03 − 05

郑文锋(1969 − )，男，博士，副教授，主要从事空间信息科学、地球探测与信息技术方面的研究.