一种快速准确适用性广的伪随机扰码识别方法
2015-10-09虞红芳杜宇峰
虞红芳,吴 曼,刘 曼,杜宇峰
(1. 电子科技大学通信与信息工程学院 成都 611731;2. 中国电子科技集团公司第五十四研究所 石家庄 050081)
一种快速准确适用性广的伪随机扰码识别方法
虞红芳1,吴 曼1,刘 曼1,杜宇峰2
(1. 电子科技大学通信与信息工程学院 成都 611731;2. 中国电子科技集团公司第五十四研究所 石家庄 050081)
针对高误码率下的伪随机扰码快速盲识别问题,提出了一种结合基于m序列统计特征和基于卷积的快速相关攻击算法的盲识别方法。该方法通过基于m序列统计特性快速获得扰码器生成多项式和通过快速相关攻击准确获得扰码器初态。仿真实验表明,该方法与基于枚举法的扰码识别方法和快速相关攻击的扰码识别方法相比,在识别时间和识别正确率方面都有更好的性能表现。
误码率; 盲识别; 快速相关攻击; m序列统计特性; 伪随机扰码
在通信领域中,实际的数字通信系统为了提高性能,信号在传输前常采用扰乱编码技术以改变其传输特性。加扰在提高信号传输安全性的同时也使原始信息变为充分随机化的信号,因此,研究如何快速正确地识别对方采用的扰码显得尤为重要。
从扰码序列是否独立用于加扰的伪随机序列来看,扰码可以分为自同步扰码和伪随机扰码两种。两种扰码识别的区别主要在于自同步扰码识别只需要识别扰码器结构;而伪随机扰码识别在识别扰码器结构的基础上还需要识别扰码器的初态。本文主要研究伪随机扰码的识别问题。
1 研究现状
文献[1]采用Walsh变换法对扰码序列的生成多项式进行测定,文献[2]基于文献[1]改进了对扰码序列的初态进行恢复的快速相关算法。但是Walsh-Hadamard法对自同步扰码进行识别时,当输入信息中含1率在46%~50%时正确率不高;对伪随机扰码,该方法仅能识别出生成多项式,无法对扰码初态进行识别。
文献[3]利用信道序列的游程特点粗略估计扰码器多项式阶数的范围,然后运用组合枚举求优势的还原方法对扰码器结构进行识别。文献[4]充分利用了伪随机序列中存在的线性相关性以及概率论中正态分布的优势理论,但在识别伪随机扰码的寄存器初态时,对扰码器输入的消息序列中含1率有要求(一般不超过20%)。
文献[5]提出的基于m序列统计特性的扰码识别方法,充分利用m序列良好的伪随机性进行游程特性的统计以及序列本身的递推关系,还原产生m序列的线性反馈移位寄存器。该方法适用于自同步扰码生成多项式的识别分析,但并不适用于对伪随机扰码识别。
文献[6-10]提出了基于卷积相关攻击法的扰码识别方法。特别地,文献[8]提出一种针对序列密码改进的快速相关攻击算法,其将序列密码的攻击问题转化为线性分组码的译码问题,但是该算法也需要穷举扰码器初始状态,在扰码器级数较大时需要大量的穷举时间;文献[9]提出了一种自同步式伪随机扰码的盲识别法,通过组合枚举法确定生成多项式,并利用基于卷积码的快速相关攻击算法识别初态,但是该方法需要穷举LFSR的所有抽头情况,且当误码率较大时恢复无误码的初态需要找到上万个校验方程,这会导致计算量的急剧增加;文献[10]针对在高误码率下多抽头系数的伪随机扰码的盲识别问题,提出了结合BM算法与基于卷积码的快速相关攻击算法的盲识别方法,该方法可以对级数较低的伪随机扰码器进行快速准确识别,但当级数较大时,随着预估计生成多项式急剧增多,识别初态的时间也急剧增加,识别准确率明显下降。
针对现有伪随机扰码盲识别方法在识别时间效率、识别准确率和识别适用范围的局限性,以及各种方法的优势,本文提出了一种新的盲识别方法。
2 算法原理及过程
本文扰码识别算法在现有方法的基础上,有效地结合了基于m序列统计特性的扰码识别和基于卷积相关攻击的扰码识别方法,可以较好地解决在高误码率以及扰码器级数较高情况下伪随机扰码盲识别的问题。其主要由两部分组成,即基于m序列统计特性的扰码器结构识别和基于卷积相关攻击的扰码器初态识别。
2.1 基于m序列统计特性的扰码器结构识别
经扰码器加扰后的信道序列具有与组成该扰码器的寄存器产生的m序列相近的特性,按照游程统计特征,确定级数l的范围。对每一个可能的l值,在每种可能的抽头位置下,统计满足m序列递推关系的个数:
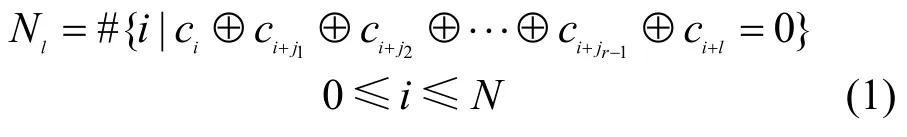
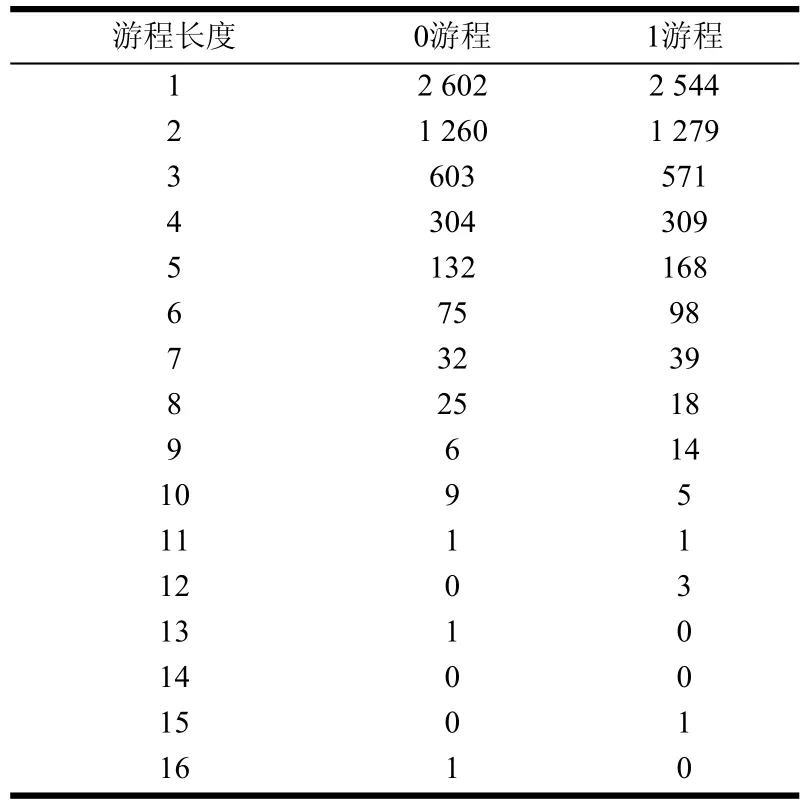
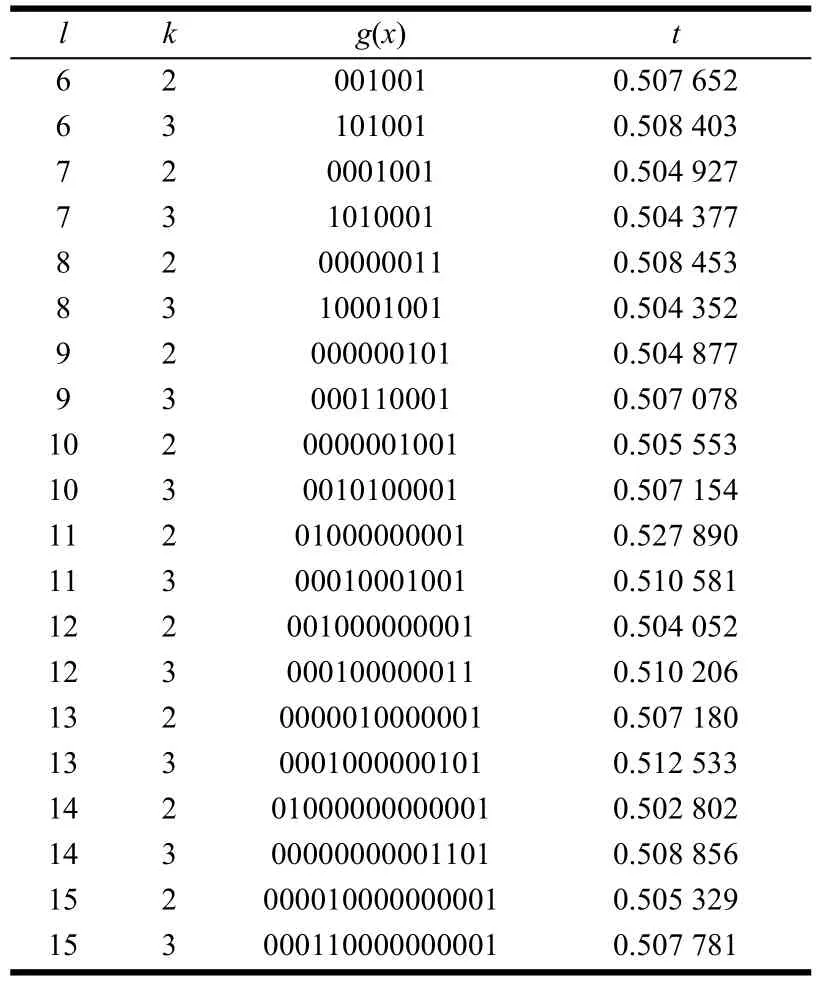
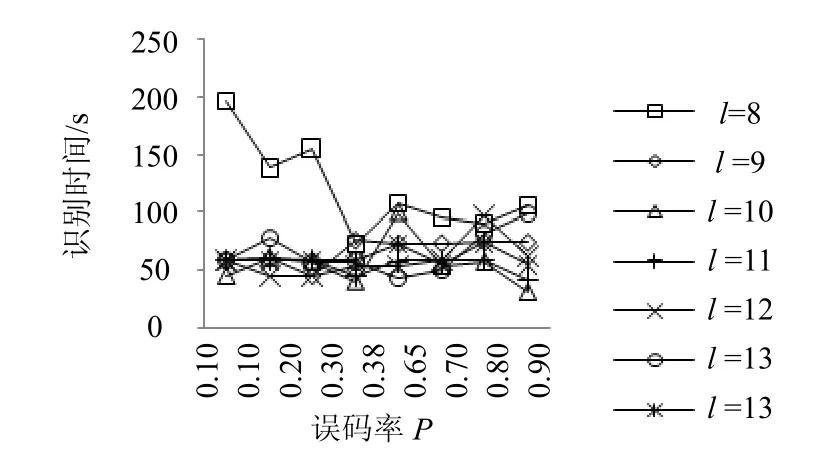
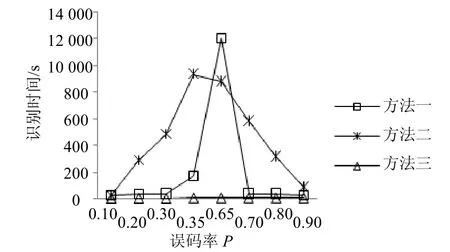
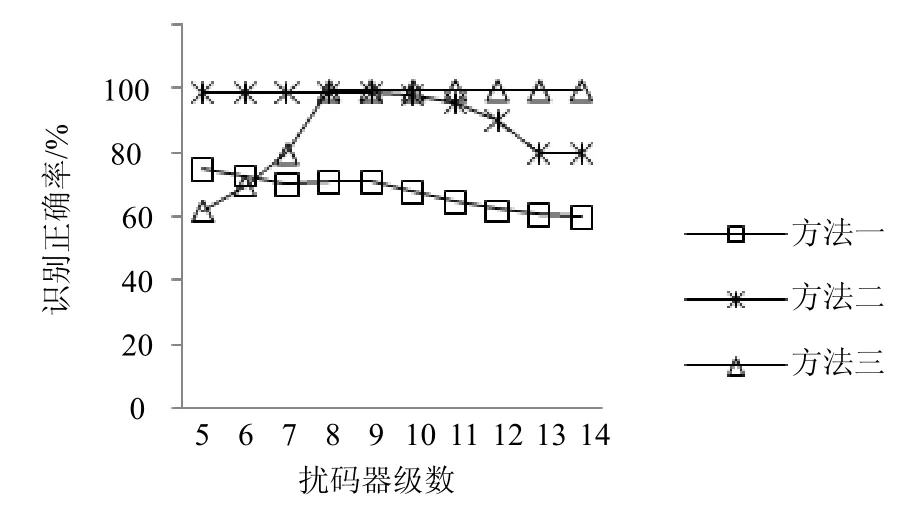
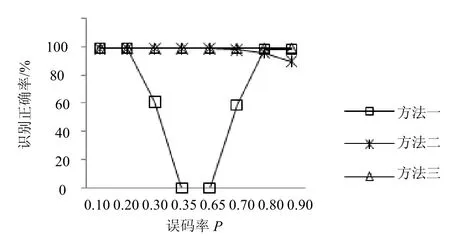
式中,0 2.2 基于卷积相关攻击的扰码器初态识别 1) 构造生成矩阵和编码矩阵 对g(x)有LFSR序列un满足: 并且根据 2) 对卷积码序列进行Viterbi译码 在信道序列位置Location(构造卷积码序列对应的信道序列位置,其初始值为1)处,分别截取信道序列Z和Z*(Z*为将接收到的信道序列中1变为0,0变为1得到的序列),分别与生成矩阵GLFSR构造卷积码序列rn和在译码时遍历2B个译码初始状态以得到准确的译码结果。 3) 通过误码率与阈值比较确定扰码器初态 当Comp<ρ(ρ为设置比较误码率Comp的阈值,其初始值为0.1),且ρ<0.5,则为最后识别的扰码器初态,识别结束。 当Comp*>*ρ(*ρ为设置比较误码率Comp*的阈值,其初始值为0.9),且*ρ>0.5,则为最后识别的扰码器初态,识别结束。 当Comp>ρ(或Comp*<*ρ)且ρ<0.5(或*ρ>0.5),将Location值增加1; 当Location值小于10l,重复以上步骤;当Location值大于10l,阈值ρ增加0.05,阈值*ρ减少0.05,同时将Location值恢复成初始值,重复以上步骤。 2.3 算法流程 图1为基于m序列统计特性和卷积相关攻击的扰码识别算法流程图。 图1 基于m序列统计特性和卷积相关攻击的扰码识别算法流程图 3.1 实例分析 为验证本文算法,以接收信道序列长度为20 kb,扰码器生成多项式为g(x)=1+x2+x11,初态为10000001000,误码率为0.3,设置比较误码率为0.35为例,进行扰码盲识别和恢复的仿真试验。 表1 伪随机扰码游程统计结果 1) 先进行游程统计和寄存器级数初识别。表1为伪随机扰码的游程统计结果,由统计结果可以看出,在l=5附近,1/2递减规律开始不明显;在l=16附近,游程个数开始趋于0,由判决标准可以确定级数l的范围为5<1<16。 表2 基于m序列统计特征得到的优势值与抽头(k)关系 表2中列出了每个可能的级数对应的一定抽头数下最大优势值。 2) 对5<1<16,分别统计可以发现01000000001结构对应的优势值(0.527 89)最大,故得到扰码器生成多项式为g(x)=1+x2+x11;再根据该生成多项式构造出其生成矩阵以及编码矩阵;最后将构造的卷积码序列进行Viterbi译码,得到预估计初态为10000001000,根据误码率比较可以确定该预估计初态即为扰码器初态。不同抽头情况下的优势值,其统计结果如表2所示。 3.2 性能分析 采用本文提出的扰码识别方法对不同扰码器结构以及不同误码率分别进行测试,并与基于枚举法的扰码识别方法和基于相关攻击的扰码识别方法进行了比较。 图2所示为基于m序列统计特性和卷积相关攻击的扰码识别方法在不同误码率P值的情况下,不同扰码器级数对应的识别时间,通过该图可以看出新方法随着扰码器的移位寄存器个数的增多识别时间并没有急剧增加,即扰码器级数越大本文方法在识别时间上的优势越明显,这是因为该方法首先采用m序列的统计特性得到了扰码器结构,而在已知扰码器结构的情况下,利用卷积相关攻击算法就可以较快地识别出扰码器初态。 图2 不同扰码器级数在不同误码率时的识别时间 图3为在扰码器级数9l=的情况下,3种扰码识别方法在不同误码率时的识别时间,其中方法一代表基于枚举法的扰码识别方法,方法二代表基于卷积相关攻击的扰码识别方法,方法三代表基于m序列统计特性和卷积相关攻击的扰码识别方法。从图中可以看出,基于枚举的扰码识别方法和基于卷积相关攻击的扰码识别方法随着误码率向0.5靠近时,识别的时间急剧增加,而基于m序列统计特性和卷积相关攻击的扰码识别方法在各误码率情况下变化不大,这是由于基于枚举法的扰码识别对扰码器输入的消息序列中含1量要求较高,而基于卷积相关攻击的扰码识别方法当误码率较大时,恢复无误码的初态需要找到上万个校验方程,这都会导致计算量的急剧增加。 图3 9l=,在不同误码率下3种方法的识别时间 图4为在不同扰码器级数情况下,3种扰码识别方法识别的平均正确率。从图中可以看出,基于枚举的扰码识别方法和基于卷积相关攻击的扰码识别方法随着扰码器移位寄存器个数增加识别的平均正确率下降,这是因为随着扰码器级数的增加,枚举法要遍历的初态成指数增加,卷积相关攻击法译码长度也增加,导致了这两种方法识别正确率下降。本文提出的扰码识别方法识别的平均正确率反而提高,表明该方法更适用于扰码器级数较高的情况。 图4 不同扰码器级数,3种方法识别的平均正确率 图5为在扰码器级数9l=的情况下,3种扰码识别方法在不同误码率时的识别正确率。从图中可以看出,在扰码器级数为9时,基于枚举法的扰码识别方法只能正确识别误码率低于0.2的伪随机扰码,基于卷积相关攻击的扰码识别方法和基于m序列统计特性和卷积相关攻击的扰码识别方法都可以得到较好的识别正确率。 图5 9l=,3种方法识别正确率的比较 综上,基于枚举法的扰码识别方法识别结果的正确性受到误码率的限制,这是由于该算法本身是基于扰码序列自相关性的强弱来判断扰码器结构的,而当误码率较大时,对扰码序列的自相关性有较大影响,即会影响扰码识别的结果;对基于卷积相关攻击的扰码识别方法,当扰码器生成多项式级数越大时,识别的时间越长。当多项式级数较低时,基于m序列统计特性和卷积相关攻击的扰码识别方法与快速相关攻击算法比较,其时间效率较低,即没有明显优势;但随着多项式级数增加,特别是当级数增加到10以上时,其正确识别的时间效率明显地提高了。所以新方法识别的时间效率有所提高,且准确率也大大提高。 本文创新点在于将传统识别方法中的基于m序列统计特性法和卷积相关攻击法相融合,得到一种全新的识别伪随机码的方法——结合了m序列统计特性识别扰码器生成多项式和卷积相关攻击识别扰码器初态的优势。与基于m序列统计特性的扰码识别方法比较,本文方法可以对伪随机扰码器的初态进行识别,并且在进行初态识别时不需要对所有初态进行遍历,而是利用卷积相关攻击快速求解初态,大大降低了识别高级数的扰码器初态的时间,即在识别时间效率上得到提高。与卷积相关攻击方法比较,本文方法不用求解预估计生成多项式集合,而是利用基于m序列统计特性的扰码识别方法求解出准确的生成多项式,提高了识别多项式和初态的准确率。另外,现有的伪随机扰码识别方法需要知道扰码器输入信息序列1、0比例,且限制1、0比例不在0.4左右。本文方法不需要提前知道该比例,且可以快速准确识别输入序列1、0比例在0~0.4和0.6~1之间的扰码器生成多项式和初态,扩大了适用性。 [1] 伍文君, 黄芝平, 唐贵林, 等. 含错扰码序列的快速恢复[J]. 兵工学报, 2009, 30(8): 1134-1138. WU Wen-jun, HUANG Zhi-ping, TANG Gui-lin, et al. Fast recovery of interfered scrambling code sequence[J]. Acta Armamentarii Sinica, 2009, 30(8): 1134-1138. [2] 游凌, 朱中梁. Walsh函数在解二元域方程组上的应用[J].信号处理, 2000, 16(12): 27-30. YOU Ling, ZHU Zhong-liang. The application of Walsh function in resolving of F(2) equations[J]. Signal Processing, 2000, 16 (12): 27- 30. [3] 黄芝平, 周靖, 璟苏绍. 基于游程统计的自同步扰码多项式阶数估计[J]. 电子科技大学学报, 2013, 42(4): 541-545. HUANG Zhi-ping, ZHOU Jing, SU Shao-jing. Order estimation of self-synchronizing scrambling polynomial based on run statistic[J]. Journal of University of Electronic Science and Technology of China, 2013, 42(4): 541-545. [4] 朱洪斌. 对伪随机扰码和自同步扰码的盲识别[J]. 科技风, 2010(14): 220-221. ZHU Hong-bin. Blind recognition of pseudo-random scrambling and self-synchronizing scrambling[J]. Technological Wind, 2010(14): 220-221. [5] 朱华安, 谢端强. 基于m序列统计特性的序列密码攻击[J].通信技术, 2003(8): 96-98. ZHU Hua-an, XIE Duan-qiang. Attacks upon stream cipher based on m-sequence’s statistical property[J]. Communications Technology, 2003(8): 96-98. [6] THOMAS J, FREDRIK J. Theotetical analysis of a correlation attack based on convolutional codes[J]. IEEE Transactions on information theory, 2002, 48(8): 2173-2181. [7] THOMAS J, FREDRIK J. Improved fast correlation attacks on stream ciphers via convolutional codes[DB/OL]. [2009-05-20]. http://www.springerlink.com/ content/. [8] 伍文君, 唐贵林, 黄芝平. 一种快速相关攻击算法[J]. 计算机工程, 2009, 35(17): 129-131. WU Wen-jun, TANG Gui-lin, HUANG Zhi-ping. Fast correlation attack algorithm[J]. Computer Engineering, 2009, 35(17): 129-131. [9] 罗向阳, 沈利, 陆佩忠, 等. 高容错伪随机扰码的快速盲恢复[J]. 信号处理, 2004, 20(6): 552-558. LUO Xiang-yang, SHEN Li, LU Pei-zhong, et al. Fast blind restore of LFSR sequences with error tolerance[J]. Signal Processing, 2004, 20(6): 552-558. [10] 郝士琦, 戚林, 王勇. 一种新的伪随机扰码识别方法[J].电路与系统学报, 2011, 16(4): 6-12. HAO Shi-qi, QI Lin, WANG Yong. A new blind recognition method of pesudo-randomizer code sequence [J]. Journal of Circuits and System, 2011, 16(4): 6-12. 编辑张 俊 Fast and Correct Recognition Method for Pseudo-Randomizer Code YU Hong-fang1, WU Man1, LIU Man1, and DU Yu-feng2 To solve the recognition of pseudo-randomizer code under the condition of high bit-error rate, a new blind recognition method is proposed. Combining the statistical property of m-sequence and fast correlation attack mechanism based on convolutional codes, this method can fast recognize the generating polynomial based on m-sequence’s statistical property and correctly find the initial state of linear feedback shift register (LFSR) through fast correlation attack mechanism. The simulation results show that this method outperforms exiting solutions (e.g., enumeration based solution and fast correlation attack based solution) in terms of recognition time and correct rate. bit-error rate; blind recognition; fast correlation attack; m-sequence’s statistical property; pseudo-randomizer code TP911.4 A doi:10.3969/j.issn.1001-0548.2015.04.004 2014 − 03 − 18; 2014 − 12 − 11 国家973计划(2013CB329103) 虞红芳(1975 − ),女,博士,教授,主要从事网络虚拟化、软件定义网络、云计算、星地融合光网络等方面研究.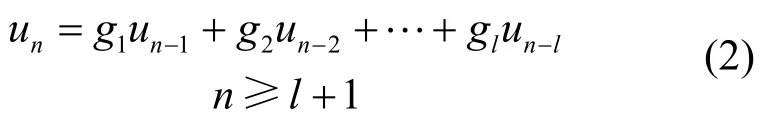
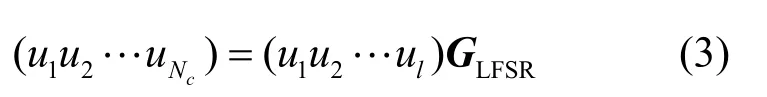
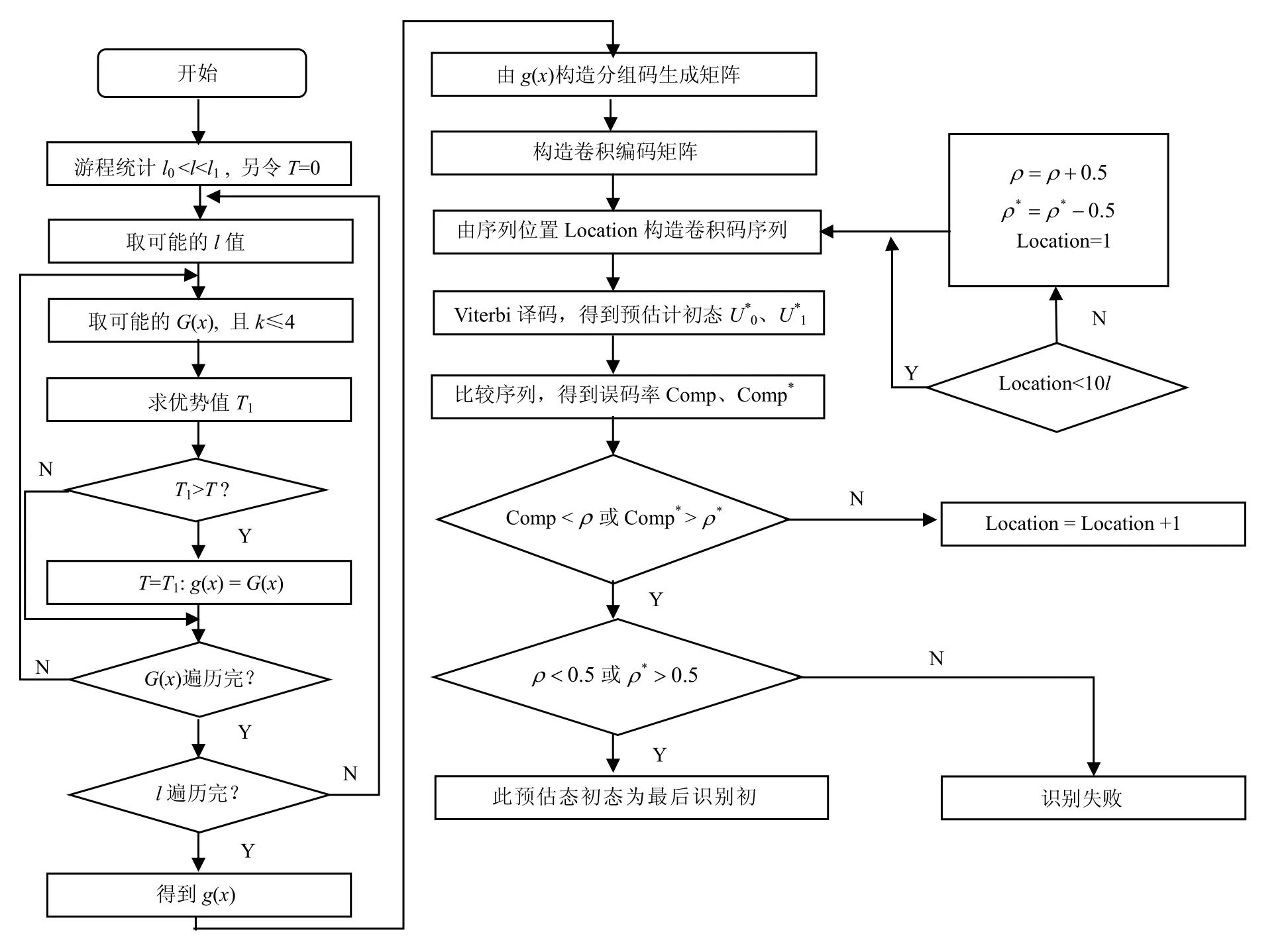
3 应用及结果分析
4 结 束 语
(1. Institute of Communication and Information Engineering, University of Electronic Science and Technology of China Chengdu 611731; 2. China Electronics Technology Group Corporation 54th Research Institute Shijiazhuang 050081)
