欠定盲分离时变混合矩阵的估计

付卫红，李爱丽，黄 坤，马丽芬，严 新，杨 博

(1. 西安电子科技大学综合业务网理论及关键技术国家重点实验室 西安 710071; 2. 航天恒星科技有限公司 北京 海淀区 100086)

欠定盲分离时变混合矩阵的估计

付卫红1，李爱丽1，黄 坤1，马丽芬1，严 新1，杨 博2

(1. 西安电子科技大学综合业务网理论及关键技术国家重点实验室 西安 710071; 2. 航天恒星科技有限公司 北京 海淀区 100086)

针对欠定盲分离中时变混合矩阵的估计问题，在稀疏域二维最小偏差角算法的基础上，提出了一种改进的欠定盲分离时变混合矩阵估计算法。该算法通过判断原始阵各列上是否都有观测点聚集和聚集在原始阵上的观测点以外的点的聚集方向，来检测变化时刻；并利用基于点密度大区域检测算法估计混合矩阵。改进算法对于混合矩阵发生某些列增加、消失和变化时均能检测出变化，并且在大幅提高变化时刻检测概率和混合矩阵估计精度的同时，降低了复杂度。实验仿真结果表明，在20 dB信噪比时，混合矩阵估计精度提高了60%以上。

盲源分离; 混合矩阵估计; 信号处理; 时变; 欠定

盲源分离[1-2]是指在一个通信系统中，源信号和信道均未知，在只有观测信号的情况下，恢复出源信号的技术。根据源信号个数和观测信号个数的不同可以分为欠定盲分离[3-4](源信号个数大于观测信号个数)和非欠定盲分离[5-7](源信号个数小于观测信号个数)两种情况。

对于欠定盲分离，目前主要集中在静态情况下的研究[8-11]，即源信号个数不变、信道不变。而实际情况中，源信号个数常会发生变化，在增加、减少或者某些源信号消失的同时又有新的源信号产生。受环境的影响，信道也在不断发生变化。对于这种时变情况下的欠定盲分离，目前研究甚少。文献[12]提出了一种源信号和混合矩阵时变情况下的欠定盲分离方法，将时变的混合矩阵的估计分为两步：1) 变化时刻的检测。通过将观测信号分帧；然后检测每帧中观测信号是否聚集在原始矩阵的各列上来判断是否发生变化。该方法适用于混合矩阵有新列增加的情况，但是当某些源信号消失时，不能检测出变化。2) 混合矩阵的估计。采用搜索重构观测信号采样点法[9]，该方法抗噪声能力较差，且受区间数影响较大。本文针对文献[12]进行改进，提出了一种改进的欠定盲分离时变混合矩阵的估计方法，即改进的变化时刻检测方法和新的混合矩阵估计算法——基于点密度大区域检测的混合矩阵估计算法。改进的变化时刻检测方法在混合矩阵发生某列增加、某列减少、某列消失的变化时均能检测出变化，而点密度大区域检测法相比于文献[12]中的搜索重构观测信号采样点法具有更高的估计精度，从而使本文方法在时变混合矩阵估计时具有更好的性能。

1 欠定盲分离的模型

考虑最简单的线性瞬时混合欠定盲分离，其数学模型可以表示为：

式中，s(t)=[s1(t),s2(t),,sn(t )]T为n维源信号矢量；x(t)=[x(t)x(t),,x(t )]T为m维观测信号矢量；m n>m；A为m×n的混合矩阵，A=[a1,a2,,an]，ai(i=1,2,,n)为A的列向量；t表示观测时刻，t=1,2,,T。若将A写成列向量的形式，则式(1)可写为：

欠定盲分离一般采用两步法：首先估计混合矩阵；然后在混合矩阵已知的基础上分离源信号。混合矩阵的估计精度直接影响分离信号的质量，因此，混合矩阵的估计在欠定盲分离中起着至关重要的作用，无论是静态还是动态情况下的盲分离。在欠定模型下，源信号和混合矩阵动态变化时，应首先估计出变化时刻，然后根据变化后的观测信号估计出变化后的新矩阵。因此，对于欠定盲分离时变混合矩阵的估计，包括检测变化时刻和估计混合矩阵。

2 变化时刻的检测

对于时变情况下的欠定盲分离，关键是检测出变化时刻，再根据变化前后的观测信号分别估计出混合矩阵。在每一次变化时，都将变化前的混合矩阵作为已知(称为原始阵)，检测观测信号聚集方向与原始阵间是否出现偏差，若连续出现偏差，则混合矩阵已发生变化，从而估计出新的混合矩阵。

文献[12]主要思想是检测观测信号是否聚集在原始阵各列上。对变化时刻的检测主要依据两个门限值：稀疏域二维最小偏差角的门限a和每帧观测信号中超出门限a的比例的门限b。

文献[12]主要依据连续数帧中有高于门限值数目的观测信号没有聚集在原始矩阵的方向上来判断变化，比较笼统，尤其在混合矩阵变化情况为某列消失时，观测信号仍然聚集在原始阵的部分列上，导致检测不出变化。门限b的设定依赖于噪声大小和混合矩阵变化的大小，不好设定。另外文献[12]需要先求出原始矩阵的方向角和观测信号的方向角，增加了计算量。

本文提出了一种改进的检测变化时刻的方法。首先分析了混合矩阵变化具体有哪些情况，在检测时，对每一帧检测原始阵各列上是否都有观测信号聚集并估计出不在原始阵各列上的观测信号的聚集方向。该方法不用计算方向角，没有门限b，且可以检测混合矩阵变化为某列消失的情况。

针对源信号和混合矩阵动态变化的情况，变化时刻检测的方法如下：将t=0,1,,T1,,T2时刻的观测信号分为M帧，每帧的观测信号点数为T2/M，按帧处理。首先，在每一帧内检测原始阵各列上是否有观测信号聚集，若某些列上连续k帧没有观测信号聚集，则混合矩阵发生改变。若原始阵上各列均有观测信号聚集，检测除聚集在原始阵上的观测点以外的点的聚集方向，若这些点连续k帧聚集在某些确定方向上，则混合矩阵发生改变。

由以上原理得到，改进的变化时刻检测方法的具体步骤如下：

1) 将观测信号进行归一化，得到X。

3) 根据第i(初始值为0)帧观测信号X(1),X(2),,X(N)估计混合矩阵A1。

4) i=i+1。

5) 检测第i帧中，原始阵A1各列是否有观测信号聚集；检测聚集在原始阵上的观测点以外的点的聚集方向。

6) 若i>2

① 若存在某些列上连续3帧没有观测信号聚集，则混合矩阵发生变化，跳到步骤7)；否则，执行②；

② 若原始阵以外的观测点连续3帧聚集在某些方向上，则混合矩阵发生变化，跳到步骤7)；否则，回到步骤4)。

7) 利用变化后的3帧观测信号估计出新的混合矩阵，并将该阵赋值给A1作为原始阵。回到步骤4)。

3 混合矩阵的估计

文献[12]对混合矩阵的估计采用了搜索重构观测信号采样点的方法，该方法抗噪声能力较差，并且涉及区间个数设置的问题，区间设置的个数对估计效果影响很大，却没有理论指导应该设置多少。下面对本文提出方法进行介绍。

3.1 点密度大区域检测法原理

在欠定情况下，当源信号充分稀疏时，观测信号具有线聚类特性，即聚集在混合矩阵A的各个列向量上。若把观测信号和混合矩阵列向量进行归一化，则观测信号聚集在A的各个列向量确定的点上。如图1所示，m=3，n=4，有噪情况下的3个观测信号x1,x2,x3的散点图。

图1 m=3、n=4情况下观测信号散点图

从图1可以看出，观测信号点清晰地分为4类。在混合矩阵列向量确定的4个点附近有较多的观测信号点。定义某个点的密度为以该点的方向为中心，以θ为角度差的方向内的观测信号点数，则位于混合矩阵A确定的4个点周围的观测信号点，其密度明显大于远离这4个点的观测信号点。而密度比较小的点往往是受噪声影响较大的点，且这些点也含有一定的有用信息。

若将这些密度比较小的点先去掉，那么剩下的点则清晰地分为4类。以保留下来的密度比较大的点为对象，随机选取某个观测点为初始点；然后按照距离原则，将离该点较近的观测点都划分为一类，将该类中的观测信号点求均值，即得到混合矩阵某列的估计。再对剩下的点随机选取一个观测信号点为初始点，按照距离原则，将离初始点较近的观测信号点划分到一类并求均值，得到混合矩阵第二列的估计。以此类推，直到所有的观测信号点都被聚类完毕，得到混合矩阵的初始估计。

将得到的混合矩阵的初始估计作为初始聚类中心，将所有的观测信号(包括点密度大的和点密度小的)以初始聚类中心开始进行k均值聚类[13]。经过k均值聚类后得到混合矩阵的精确估计。

3.2 点密度大区域检测法

1) 将观测信号进行归一化，得到观测信号X。2) 计算每个观测信号点的点密度。

3) 将点密度比较大的观测信号点筛选出来，组成集合1X。

4) 对于集合1X中的观测信号点，随机选取某个点为初始点，将离该点较近的点归到一类，并求出这一类中观测信号点的均值，该均值为混合矩阵某一列的初始估计。

5) 对于1X中未参与聚类的点重复步骤4)，直到X1中所有观测信号点都参与了聚类。

6) 将得到的混合矩阵的初始估计作为初始聚类中心，利用k均值算法对X进行聚类。

聚类中心即为混合矩阵的估计。

4 实验结果与分析

分别从变化时刻检测概率和混合矩阵估计误差两方面对本文算法及文献[12]算法进行了比较；另外研究了每帧所取点数对估计效果的影响。

4.1 仿真实验一

该实验为变化时刻检测概率的对比试验。仿真条件如下：源信号个数为n(取值为3和4)；观测信号个数m=2；源信号由函数randn随机产生，源信号长度T=4 000；分帧数M=20；信噪比SNR=15～25 dB，每个信噪比下仿真2 000次。混合矩阵A1、A2和A3分别为：

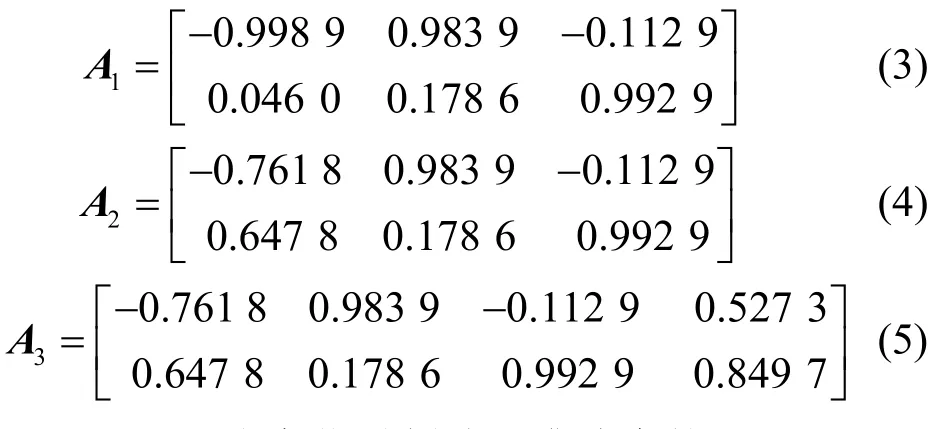
图2～图4为变化时刻估计准确度的对比图，混合矩阵均从第11帧发生变化，即1～10帧为一个矩阵，第11～20帧为变化后的矩阵。其中图2为混合矩阵从A1变化到A2时的对比图，对应混合矩阵某列发生变化的情况；图3为混合矩阵从A2变化到A3时的对比图，对应混合矩阵发生增加某列的情况；图4为混合矩阵从A3变化到A2的对比图，对应混合矩阵发生某列消失的情况。

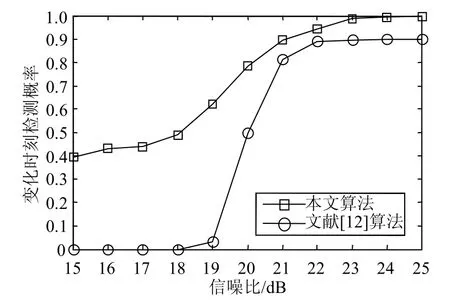
图2 混合矩阵变化一列情况下变化时刻检测概率

图3 混合矩阵增加一列情况下变化时刻检测概率

图4 混合矩阵减少一列情况下变化时刻检测概率

从图2和图3可以看出，本文方法在变化时刻检测概率方面明显高于文献[12]的算法，尤其在低信噪比时，文献[12]无法使用，而本文方法仍然可以检测出变化时刻，检测概率在30%以上。从图4可看出，在混合矩阵发生列数减少时，文献[12]完全不能使用，而本文方法不仅能够估计出变化，且准确率较高，在信噪比20 dB以上时，准确率达到80%以上。

4.2 仿真实验二

该实验为混合矩阵估计误差的对比试验。仿真条件如下：源信号个数为n(取值为3和4)；观测信号个数为m=2；源信号由函数randn随机产生，源信号长度T=600；信噪比SNR=15～25 dB，每个信噪比下仿真2 000次。混合矩阵分别为4.1节中的A1、A2和A3，分别采用搜索重构观测信号采样点法和点密度大区域检测法估计混合矩阵，混合矩阵估计误差图如图5所示。

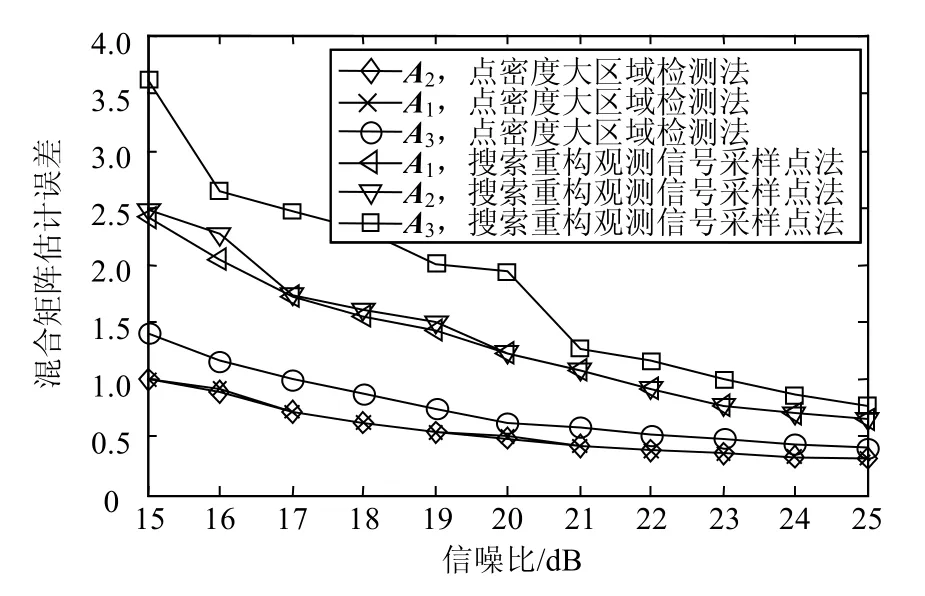
图5 混合矩阵估计误差对比

从图5可以看出，在混合矩阵估计精度方面，点密度大区域检测法明显优于搜索重构观测信号采样点法，如在信噪比为20 dB时，对矩阵A1、A2和A3的估计精度，点密度大区域检测法分别比搜索重构观测信号采样点法提高了60%、60%和65%，这是因为点密度大区域检测法抗噪声能力较强，而搜索重构观测信号采样点法不仅抗噪能力差，而且区间数的设置不好把握。由于点密度大区域检测法对混合矩阵的估计精度较高，结合改进算法中提出的变化时刻检测方法，使得改进的时变欠定盲分离混合矩阵估计算法在时变混合矩阵估计中具有很好的性能。

4.3 仿真实验三

该实验为每帧内点数N对变化时刻检测概率的影响实验。仿真条件如下：源信号个数n=4；观测信号个数m=3；源信号由函数randn随机产生，源信号长度T=4 000；信噪比SNR=15～25 dB，每个信噪比下仿真1 000次；分帧数M=20, 40, 80，对应的每帧内的点数N=200, 100, 50。变化前的混合矩阵为A4，变化后的混合矩阵为A5。当M=20时，混合矩阵从第11帧变化为矩阵A5；当M=40时，混合矩阵从第21帧变化为矩阵A5；当M=80时，混合矩阵从第41帧变化为矩阵A5。参数N对检测概率的影响如图6所示。

从图6可以看出，每帧内点越多(N值越大)，检测概率越高，但是N值不宜过大，过大不容易跟踪并检测矩阵发生变化的精确时刻。一般N值取100～200比较合适。

图6 参数N对检测概率的影响

5 结 束 语

对于欠定盲分离时变混合矩阵的估计，本文提出了一种新的方法，该方法采用改进的变化时刻检测方法和新的混合矩阵估计方法——点密度大区域检测法。改进算法具有较低的复杂度，不仅提高了变化时刻的检测概率，且可以估计混合矩阵某列消失时的变化。点密度大区域检测法在估计混合矩阵方面具有更高的估计精度，和改进的变化时刻检测方法结合较原来的方法在时变混合矩阵估计时具有更好的性能。

[1] THIAGARAJAN J J, RAMAMURTHY K N, SPANIAS A. Mixing matrix estimation using discriminative clustering for blind source separation[J]. Digital Signal Processing, 2013, 23(1): 9-18.

[2] ZHANG Yan-liang, ZHANG Wei-tao, DU Jing-jing. Jeneral method to estimate mixing matrix in blind source separaton[J]. Journal of Computer Applications, 2012, 32(9): 2432-2435.

[3] XIE S, YANG L, YANG J M, et al. Time-frequency approach to underdetermined blind source separation[J]. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(2): 306-316.

[4] LU Hong, ZHAO Zhi-jin, YANG Xiao-niu. Algorithm for underdetermined blind source separation based on DANMF[J]. Journal of Computer Applications, 2011, 31(2): 553-555, 558.

[5] XUE Yun-feng, WANG Yu-ja, SUN Qiu-dong. A novel method for overdetermined blind source separation[C]//The 2nd International Conference on Information Science and Engineering. NewYork: IEEE Press, 2010.

[6] WANG Yu-ja, XUE Yun-feng. Overdetermined blind source separation by Gaussian mixture model[C]//Advanced Intelligent Computing Theories and Applications. With Aspects of Artificial Intelligence. Berlin: Springer, 2011.

[7] YE Ji-min, ZHANG Xian-da, JIN Hai-hong. Semiparametric statistical approach for overdetermined blind source separation[J]. Dianbo Kexue Xuebao/Chinese Journal of Radio Science, 2006, 21(3): 331-336.

[8] 谭北海, 谢胜利. 基于源信号数目估计的欠定盲分离[J].电子与信息学报, 2008, 30(4): 863-867. TAN Bei-hai, XIE Sheng-li. Underdetermined blind source separation based on source’s number estimation[J]. Journal of Electronics & Information Technology, 2008, 30(4): 863-867.

[9] 白琳, 陈豪. 欠定情形下语音信号盲分离的新方法[J]. 计算机应用研究, 2010, 30(4): 863-867. BAI Lin, CHEN Hao. New method of underdetermined blind voice source separation[J]. Application Research of Computers, 2010, 30(4): 863-867.

[10] YI Qing-ming. Blind source separation by weighted k-means clustering[J]. Journal of System Engineering and Electronics, 2008, 19(5): 882-887.

[11] YANG Jing, ZHANG Yu-jie, LI Hong-wei. Underdetermined blind source separation algorithm based on k-means clustering and potential function[J]. Telecommunications Science, 2012, 28(1): 98-101.

[12] 白琳, 陈豪. 欠定模型下源信号及混合矩阵动态变化时的盲分离[J]. 电子科技大学学报, 2012, 41(3): 348-354. BAI Lin, CHEN Hao. Underdetermined blind source separation of dynamic sources and mixing matrix[J]. Journal of Electronic Science and Technology, 2012, 41(3): 348-354.

[13] LI Y, CICHOCKI A, AMARI S. Analysis of sparse representation and blind source separation[J]. Neural computation, 2004, 16(6): 1193-1234.

编辑张 俊

Time-Varying Mixing Matrix Estimation for Underdetermined Blind Source Separation

FU Wei-hong1, LI Ai-li1, HUANG Kun1, MA Li-fen1, YAN Xin1, and YANG Bo2
(1. State Key Laboratory of Integrated Service Networks, Xidian University Xi’an 710071; 2. Space Star Technology Co., Ltd. Haidian Beijing 100086)

Aiming at the problem of time-varying mixing matrix estimation in underdetermined blind source separation, an improved time-varying mixing matrix estimation algorithm is presented based on the method of planar minimum offset angle of sparse domain. By determining whether the original columns has observed the signals and the direction of the observed signals that are not in the direction of the original matrix the change time instant can be detected. The mixing matrix can be estimated by the method called the large point density area detecting. The improved algorithm can detect the changes of the columns increasing, disappearing and changing. Moreover, the detection probability of the changed time instant and the estimation accuracy of the mixing matrix are substantially increased, while the complexity of the algorithm is decreased. Experimental results show that when SNR is 20 dB, the estimation accuracy of the mixing matrix is improved by more than 60%.

blind source separation; mixing matrix estimation; signal processing; time-varying; underdetermined

TP911.7

A doi:10.3969/j.issn.1001-0548.2015.04.006

2014 − 03 − 04;

2015 − 04 − 09

国家自然科学基金(61201134, 61201135)；中央高校基本科研业务费专项资金(72124669)；高等学校学科创新引智计划(B08038)；重大专项(2012ZX03001027-001)；中国航天科技集团公司卫星应用研究院创新基金(2014_CXJJ-TX_06)

付卫红(1979 −)，女，博士，副教授，主要从事宽带无线通信、通信信号处理方面的研究.