分类讨论法解一类恒成立问题的模型探究

苏凡文

在近几年的高考题中，利用分类讨论法解一类与恒成立有关的求参问题屡次出现，此类求参问题有个共同的特征，即“在某区间上不等式恒成立，区间的端点或区间内的某一点使不等式对应的方程成立”.笔者根据此类题目的特点，整理出了几类模型，供同仁参考.

模型一

函数f（x）中含参数r，且r∈U.在区间（a，b）上f（x）>0恒成立（或在区间[a，b）上f（x）≥0恒成立），且f（a）=0，则

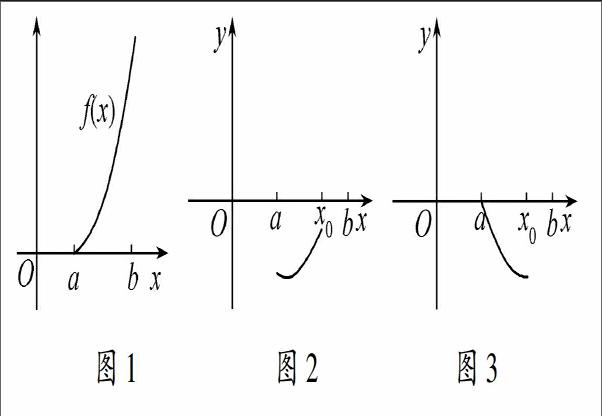
（1）对函数f（x）求导，直至f（m）（a）=0（m≤n-1），令f（n）（x）≥0在（a，b）上恒成立，求出r的取值集合A为止，然后依次推至函数f（x）为增函数（如图1），满足条件.

（2）当参数r∈

瘙 綂 [KG-3.5mm]UA时，对函数f（x）求导，直至f（m）（a）=0（m≤n-1）恒成立，且f（n）（a）<0，则x∈（a，x0）使得f（n）（x）<0，函数f（n-1）（x）在（a，x0）内为减函数，依次推至f′（x）<0（如图2），函数f（x）在（a，x0）内为减函数（如图3），得f（x）<0，与f（x）>0（或f（x）≥0）恒成立矛盾.

由（1）（2）得，参数r的取值集合为A.

图1图2图3

例1（2014年新课标Ⅱ理21改编）已知函数f（x）=ex-e-x-2x，设g（x）=f2x-4bf（x），当x>0时，g（x）>0，求b的最大值.

解析g（x）=e2x-e-2x-4x-4b（ex-e-x-2x），（x>0）.

g′（x）=2e2x+2e-2x-4-4b（ex+e-x-2），（x>0）.

若g′（x）≥0恒成立，则2（ex-e-x）2-4b（ex2-e-x2）2≥0，（ex2+e-x2）22≥b.

因为（ex2+e-x2）2>4，所以b≤2，此时g（x）在（0，+∞）上为增函数，因为g（0）=0，所以g（x）>0恒成立.

b>2时，g″（x）=4e2x-4e-2x-4b（ex-e-x），（x>0）.

g（x）=8e2x+8e-2x-4b（ex+e-x），（x>0）.

因为g（0）=16-8b<0，所以x∈（0，x0）使得g（x）<0，则g″（x）在（0，x0）上为减函数，因为g″（0）=0，则g″（x）<0，所以g′（x）在（0，x0）上为减函数，因为g′（0）=0，则g′（x）<0，所以g（x）在（0，x0）上为减函数，则g（x）<0，与g（x）在（0，+∞）上满足g（x）>0恒成立矛盾.

综上可知，b的最大值为2.

模型二

函数f（x）中含参数r，且r∈U.在区间（a，b）上f（x）<0恒成立（或在区间[a，b）上

f（x）≤0恒成立），且f（a）=0，则

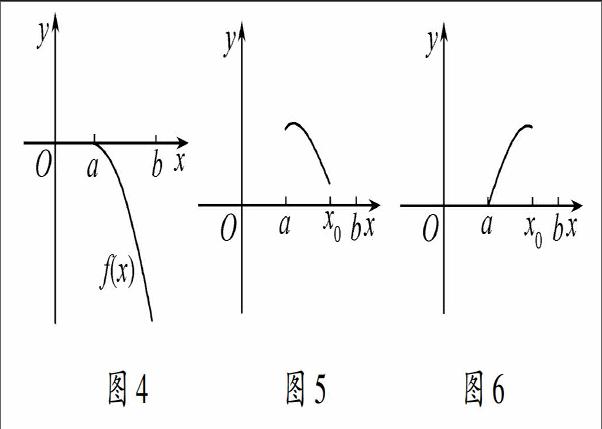
（1）对函数f（x）求导，直至f（m）（a）=0（m≤n-1），令f（n）（x）≤0在（a，b）上恒成立，求出r的取值集合A为止，然后依次推至函数f（x）为减函数（如图4），满足条件.

（2）当参数r∈

瘙 綂 [KG-3.5mm]UA时，对函数f（x）求导，直至f（m）（a）=0（m≤n-1）恒成立，且f（n）（a）>0，则x∈（a，x0）使得f（n）（x）>0，函数f（n-1）（x）在（a，x0）内为增函数，依次推至f′（x）>0（如图5），函数f（x）在（a，x0）内为增函数（如图6），得f（x）>0，与f（x）<0（或f（x）≤0）恒成立矛盾.

图4图5图6

例2（2012年天津理20改编）已知函数f（x）=x-ln（x+1）的最小值为0，对任意的x∈[0，+∞），有f（x）≤kx2成立，求实数k的最小值.

解析令g（x）=f（x）-kx2，则g（x）=x-ln（x+1）-kx2，x∈[0，+∞）.

问题转化为“对任意的x∈[0，+∞），有g（x）≤0成立，求实数k的最小值”.

g′（x）=-x（2kx-1+2k）x+1，x∈（0，+∞）.

若g′（x）≤0恒成立，则2kx-1+2k≥0，k≥12（x+1），因为x>0，所以0<12（x+1）<12，于是得k≥12，此时g（x）在[0，+∞）上为减函数，因为g（0）=0，所以g（x）≤0恒成立.

k<12时，令h（x）=-x（2kx-1+2k），x∈（0，+∞）.h′（x）=-4kx+1-2k，h′（0）=1-2k>0.所以x∈（0，x0）使得h′（x）>0，则h（x）在（0，x0）上为增函数，所以h（x）>h（0）=0，即g′（x）>0，所以g（x）在（0，x0）上为增函数，于是可得g（x）>g（0）=0，与g（x）≤0恒成立矛盾.

综上可知k≥12，即实数k的最小值为12.

注“在区间（a，b）上f（x）<0恒成立（或在区间[a，b）上f（x）≤0恒成立），且f（a）=0”可转化为“在区间（a，b）上g（x）=-f（x）>0恒成立（或在区间[a，b）上g（x）=-f（x）≥0恒成立），且g（a）=0”，于是模型二转化为模型一.

模型三

函数f（x）中含参数r，且r∈U.在区间（a，b）上f（x）>0恒成立（或在区间（a，b]上

f（x）≥0恒成立），且f（b）=0，则

（1）对函数f（x）求导，直至f（m）（b）=0（m≤n-1），n为奇数时，令f（n）（x）≤0，n为偶数时，令f（n）（x）≥0，求出r取值集合A为止，然后依次推至函数f（x）为减函数（如图7），满足条件.

（2）当参数r∈

瘙 綂 [KG-3.5mm]UA时，对函数f（x）求导，直至f（m）（b）=0（m≤n-1）恒成立，n为奇数时，f（n）（b）>0，则x∈（x0，b）使得f（n）（x）>0，函数f（n-1）（x）在（x0，b）内为增函数；n为偶数时，f（n）（b）<0，则x∈（x0，b）使得f（n）（x）<0，函数f（n-1）（x）在（x0，b）内为减函数，依次推至f′（x）>0（如图8），函数f（x）在（x0，b）内为增函数（如图9），得f（x）<0，与f（x）>0（或f（x）≥0）恒成立矛盾.