列一元一次方程解应用题的教学策略
2015-09-29林巧容
林巧容
【摘 要】2011年版《数学课程标准》要求学生在数学的学习过程中运用数学思维方式进行思考,培养发现问题、提出问题、分析问题和解决问题的能力,增强应用意识,提高实践能力,发展创新意识。
【关键词】一元一次方程 应用题 教学策略
2011年版《数学课程标准》要求学生在数学的学习过程中运用数学思维方式进行思考,培养发现问题、提出问题、分析问题和解决问题的能力,增强应用意识,提高实践能力,发展创新意识。而列方程解应用题是初中代数学习在应用上的出发点,是开发学生智力、培养分析问题、解决问题能力的重要环节,为今后学习不等式、方程组、函数等知识提供思想和方法,也为几何求值题的解题思路提供模型思想,是初中数学的重中之重。
初一学生的特点是思维活跃、肤浅,思考问题尚欠深刻,综合性较差。而列方程解应用题在“审”“设”“找”“列”“检”“答”的环节须经历抽象、建模等深刻思考才能顺利解题,因此,历来是教学的一个难点。新教材为了分散难点已作了充分的准备。比如,在小学编进了《简易方程》,让学生对列方程解应用题在思维和解法上积累经验;在初一第三章学习了列代数式,让学生能从探索具体问题中的数量关系和变化规律中,掌握用代数式进行表达的方法;新教材还在“认识一元一次方程”中举了大量与生活密切相关的应用题,设出未知数,让学生列出方程。这些举措从心理上有效减轻了学生学习应用题的恐惧心理,也从思想方法上积累了大量解题经验。但是,初中应用题加大了题目的复杂程度,学生在解题上存在如下问题:1.找不出隐含的等量关系。2.不懂灵活地设未知数。3.不懂如何使用等量关系。因此,列方程解应用题依然是教学的难点。费赖登塔尔德提出了再创造理论:数学课堂教学主要是运用问题的解决来启迪、培养和优化学生的思维品质,教师的任务是通过问题的设计为学生的发现和创造提供自由广阔的天地,进一步引导学生探索,自行挖掘其中蕴含的值得深思的问题。因此,我的教学策略是设计恰当的问题,在问题的思考和解决中以突破以上三个问题为抓手,立足于学生思维能力的培训,引导学生思考知识间的内在联系,注重分析过程的思路开拓与规律的揭示,从而感悟数学思想和方法,培养学生分析问题和解决问题的能力。
一、在问题情境思考中寻找等量关系的策略
引导学生思考知识之间的内在联系:方程是含有未知数的等式,有等式必须要有等量关系。因此列方程解应用题必须要学会找等量关系。如何寻找呢?下面通过例题的示范和回放已学过的例子来归纳总结寻找等量关系的策略。
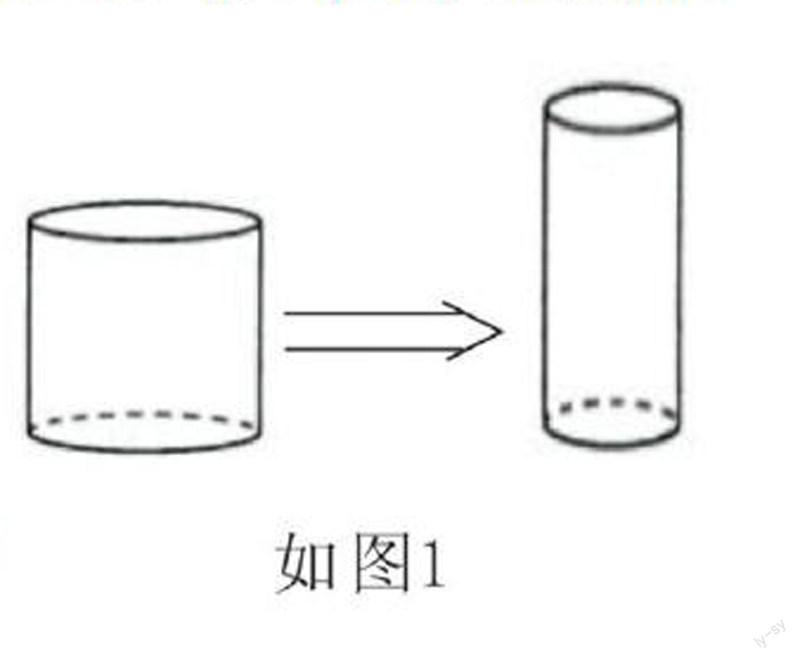
例题示范(教科书中的例题):某居民楼顶有一个底面直径和高均为4m的圆柱形储水箱(如图1),现对该楼进行维修改造,为减少楼顶原有储水箱的占地面积,需要将它的底面直径由4m减少为3.2m,那么在容积不变的前提下,水箱的高度由原先的4m变为多少米?引导学生思考探索得出:变化前后的不变量就是等量关系——旧水箱的容积=新水箱的容积。根据班级学生的实际情况,对教材进行再创造,丰富学生的数学活动经验,提高思维水平。
链接练习:铜仁市对区主干道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等,如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完,问原有树苗多少棵?
引导学生分析思考:两种假设中道路的长度总是不变的。因此,可设原有树苗x棵,根据两种不同栽树方法的道路长度一样,列方程5(x+21-1)=6(x-1)。通过例题示范和练习的链接让学生明白等量关系的一种找法:变化前后不变的量就是一个等量关系。
下面通过课件回放第一节认识“一元一次方程”的五个引例,引导学生归纳出等量关系的另外两种找法。
题目中有明显的数量关系就是等量关系。回放第三个引例:甲、乙两地相距22km,张叔叔从甲地出发到乙地,每小时比原计划多走1km,因此提前12min到达乙地。张叔叔原计划每小时走多少千米?引导学生分析思考:题目中明显的数量有“多”“提前”,因此本题等量关系有两个:①实际每小时行走的路程=原计划每小时行走的路程+1km;②实际行走时间=原计划行走时间-12min。引导学生关注题中“和”“差”“倍”“分”等表示数量关系的词语,如“一共”“多”“少”“快”“慢”“提前”“超过”“剩余”“增产”“降低”“上升”等,指出:数量关系的落实在数学运算上具有相对性。注意辨析:“几年后”与“第几年”,“翻一番”与“翻两番”, “是几倍”与“增加几倍”“增加到几倍”“增加百分之几”“增加几分之几”,“除”与“除以”等细节上的表达,要咬文嚼字,分辨清楚,注意细节。
3.挖掘问题中出现的公式,公式本身就隐含着等量关系。回放第五个引例:某长方形操场的面积是5850m2,长和宽之差为25m,这个操场的长与宽分别是多少米?引导学生观察、分析和思考:题中有一个明显的数量关系“差”,有一个公式“长方形的面积”。因此,本题有两个等量关系:①长方形的面积=长×宽;②长方形的长-长方形的宽=25m。通过以往问题的经验归纳和回放引例示范,让学生发现不同类型的应用题中都隐含有不同的公式,如行程问题:路程=速度×时间;工程问题:工作量=工作效率×工作时间;利润问题:利润率=利润÷进价,利润=售价-进价;价钱问题:总价=数量×单价;等等。
二、在解决问题的过程中引出三种设未知数的方法
引导学生思考知识之间的内在联系,方程是含有未知数的等式,因此列方程解应用题必须设未知数,未知数怎样设呢?有几种设法?下面通过例子的讲解感悟未知数的三种设法。
第一种:直接设元法。题目求什么,就直接设什么,然后寻找一个能体现题目主要意思的等量关系,列一个方程即可。这种方法应用最广,学生最爱用,也用得最好,这部分不讲,让学生自主探究,把学习的主动权还给学生。
第二种:间接设元法。有的题目用直接设元法根本无法求出,转而用间接设元法。
例题示范:在我们的身边有些股民,在每一次的股票交易中都可能盈利或亏损,某股民将甲、乙两种股票卖出,甲种股票卖出1500元,盈利20%;乙种股票卖出1600元,但亏损20%,该股民在这次交易中是盈利还是亏损?盈利或亏损多少元?引导启发学生思考:盈利还是亏损都是相对原价而言的,必须知道原来甲、乙两种股票的进价是多少,因此,用间接设元法,设甲种股票进价为x元,乙种股票进价为y元,则根据利润公式:利润率=利润/进价,得到(1500-x)/x=20%,解得x=1250元;(y-1600)/y=20%,解得y=2000。因为1500+1600-(2000+1250)=-150,所以亏损150元。
第三种:设辅助元。有的题目出现未知量,这个未知量我们不需要知道,但与题意关系密切,为了顺利解出问题,这时设一个辅助未知数起桥梁作用。
例题示范:某药店经营的抗病毒药品,在市场紧缺的情况下提价100%,物价部门查处后,限定其提价的幅度只能是原价的10%,则该药品现在降价的幅度是多少?引导学生思考:本题有一个明显的等量关系:药品提价的幅度是原价的10%,可用直接设元法,设降价的幅度为x,本题中原价是多少不知道,也不需要知道,但与题目密切相关,为了顺利列出方程,设原价为a元,这个a就是一个辅助未知数,起个桥梁作用,得(1+100%)a(1-x)=(1+10%)·a。因为a≠0,所以两边同除以a,得2(1-x)=1.1x,解得x=0.65。
通过以上问题的解决,学生在积极思考探索中,积累了活动经验,能根据题目灵活地设未知数,掌握设元的技巧,为顺利解决问题跨出了重要的一步。
三、通过一题多解或借助表格、线段图等形象表征法来领会等量关系的使用情况和注意事项
在北师大2013年6月第二版数学教学用书第225页有一句话“本课时的情况问题与前面的问题相比,数量关系要相对复杂一些,它包含两个等量关系”,这句话不对,在前面例子中只要是求两个问题,题中一定存在两个等量关系,只是列一元一次方程解应用题时,另一个等量关系用于列未知量,一个等量关系用于列方程。示范例子(教学用书第217页例子):用一根长为10m的铁丝围成一个长方形,使得该长方形的长比宽多1.4m,此时长方形的长、宽各为多少米?引导学生思考:本题有两个等量关系:①明显的数量关系,即长方形的长比宽多1.4m,所以等量关系为长方形的长=长方形的宽+1.4m;②题目中隐含着长方形的周长是10m,根据长方形的周长方式得等量关系为长方形的周长=2(长方形的长+长方形的宽)。可用直接设元法,设长方形的长为x米,解法1:用第①个等量关系列未知量,长方形的宽等于长方形的长-1.4m,即长方形的宽为(x-1.4)m;用第②个等量关系列方程,得2[x+(x+1.4)]=10,解得x=3.2,则x-1.4=1.8,得出答案。解法2:用第②个等量关系列未知量,长方形的宽等于长方形的周长除以2-长方形的长,即(5-x)m;用第①种等量关系列方程,得x=5-x+1.4,解x=3.2,则5-x=1.8,得出答案。引导学生明析:方法和过程不一样,结果一样,当然这当中有个最优化方案的解法,因题而异。
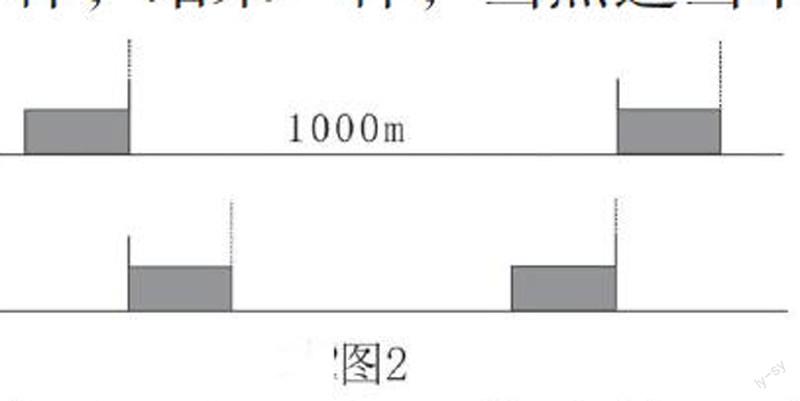
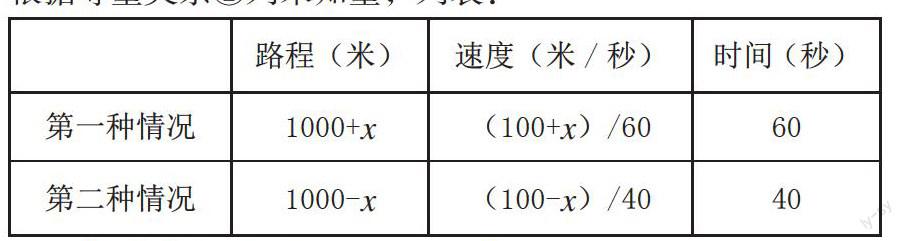
另注意:在应用题中,使用变化前后不变量作为等量关系时,完全是具体量或待定要求设元的量都不作为等量关系使用。示范例子:已知某铁路桥长1000米,现有一列火车从桥上通过,测得火车从开始上桥到完全通过桥共用了1min,整列火车都在桥上的时间为40s,求火车的车长是多少米。点拨学生可以借助线段图或表格形象表征法来分析思考:①行程问题可以借助线段图直观形象地帮助理解题意(如图2) ;②在已知量和未知量关系较模糊时可以列表格梳理思路;③引导学生找等量关系。本题是行程问题,根据路程公式本身隐含着一个等量关系:路程=速度×时间①。但题目中除了求车长一个问题外,相关的速度也是未知量,因此,还需一个等量关系。时间是完全具体量,若车长是待定要求设元的量(即用直接设元法),路程又不一样,那就从速度方面找等量关系。根据两种情况不变的是速度,因此还有一个等量关系:第一种情况的火车速度=第二种情况的火车的速度②。用直接设元法,设火车的车长为x米,根据等量关系①列未知量,列表:
路程(米) 速度(米/秒) 时间(秒)
第一种情况 1000+x (100+x)/60 60
第二种情况 1000-x (100-x)/40 40
根据等量关系②列方程得(1000+x)/60=(1000-x)/40,解得x=200。
变式:题目已知条件不变,结果改为求火车的速度。引导学生通过类比思考分析:题目中除了求火车的速度外,相关的车长也是未知量,因此除了等量关系①还需一个等量关系。时间是完全具体量,若火车的速度是待定要求设元的量(即用直接设元法),路程又不一样,那就从车长方面找等量关系。根据两种情况不变的是火车的车长,因此,另一个等量关系是:第一种情况火车的车长=第二种情况火车的车长③。用直接设元法,设火车的速度为y米/秒,根据等量关系①列未知量,列表:
路程(米) 速度(米/秒) 时间(秒)
第一种情况 60y y 60
第二种情况 40y y 40
根据等量关系③列方程,得60y-1000=1000-40y,解得y=20。
指出:本题中火车的车长与火车的速度都是不变的,为了让学生更好地理解等量关系的使用情况,可以鼓励学生用间接设元法解变式题,解法就是原题的解法,只不过把求出x=200,代入火车的速度(1000+x)/60中,得(1000+200)/60=20(米/秒)。
在列一元一次方程解应用题的一般步骤“审”“设”“找”“列”“检”“答”六个环节中,不是面面俱到,平均使力,而是提出恰当的问题,抓住学生思考问题的“关键点”,数学知识之间联系的“联结点”,数学问题变式的“发散点”,学生思维提升的“育点”和学生思维的“最近发展区”作精辟的讲解,使学生从纷繁复杂的教学内容中理出头绪,抓住问题的本质,突破难点。这种“讲”与“不讲”、“讲多”与“讲少”、“精讲”与“多练”,注重教学节奏之美的课堂,节约了很多时间,一方面可以为学生的思考提供足够的空间,另一方面可以把学习的主动权还给学生,使学生在主动、积极的情感状态下掌握知识和技能,同时也培养了分析问题、解决问题的能力。
【参考文献】
[1]翁启汉.列方程解应用题教学探讨[J].数学教学与研究,2002(16) .
[2]韩新正.谈数学课堂教学的节奏之美[J].中小学数学(初中版),2013(09).
