求解背包问题的布谷鸟搜索算法

许秋艳（盐城工学院信息工程学院，盐城　224051）

求解背包问题的布谷鸟搜索算法

许秋艳
（盐城工学院信息工程学院，盐城224051）

1　背包问题的数学模型

背包问题是计算机科学和管理科学中的一个典型优化问题，有着极其重要的研究价值。就计算时间复杂程度而言，背包问题属于经典的组合优化NP难问题。同时，背包问题在实际问题中有着广泛的应用，如材料分割问题、投资选择问题、项目组合问题等。

最经典的背包问题是0-1背包问题，该问题可以表示为：给定1个背包和n个物品，其中第i个物品的价值为pi，重量为wi，背包能够容纳的物品重量为c。现在要选择部分物品放入背包中，在保证放入物品的总重量不超过c的条件下，使得物品的总价值达到最大。背包问题的数学模型可以描述为：令pi和wi分别表示第i个物品的价值和重量，c表示背包能够容纳的物品总重量，设决策变量：

则0-1背包问题可以表示成如下的0-1整数规划模型

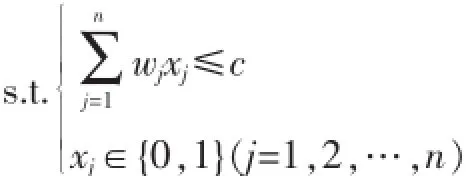
目前求解背包问题的算法可以分为传统优化算法和现代启发式算法两大类，例如分枝定界法、动态规划法、降阶法、遗传算法、蚁群优化算法、微粒群算法等等。这些方法为求解背包问题提供了思路，但都无法完全有效求解。如何设计背包问题的求解方法，仍然是一个开放性的问题。

2　背包问题的布谷鸟搜索算法

布谷鸟搜索算法是由Yang和Deb在2009年提出的一种现代启发式算法，其优化原理源于对布谷鸟寄生育雏行为和鸟类的莱维飞行行为的模拟。布谷鸟搜索算法已经在神经网络训练、工程设计优化、交通流量预测和人脸识别等方面等到成功应用。基于该算法良好的优化性能，本文将算法用于背包问题的求解。

布谷鸟搜索算法基本流程如下所示：

算法布谷鸟搜索算法

Begin

群体初始化，Xi表示第i个个体（i=1，2，…，n）

计算每个个体的适应度函数值Fi（i=1，2，…，n）While（未达到最大迭代次数）采用莱维飞行生成新解Xi

计算新解Xi的适应度函数值Fi

随机选择候选解Xj

If Fi＞Fj

采用新解替换候选解End

根据发现概率Pa舍弃差的解

保留每次迭代中产生的最好的解

End

End

上述布谷鸟搜索算法是为求解连续优化问题而提出的，为充分发挥其在处理连续优化问题的优势，仍限定算法的搜索空间为连续空间，且搜索范围为［0，1］。为将算法搜索空间的解和背包问题离散的解相对应，采用如下方法：如果Xij＞rand，则其问题对应的分量取1；否则取0。其中，Xij表示第i个解的第j个分量；rand表示0到1之间的随机数。

3　数值实验

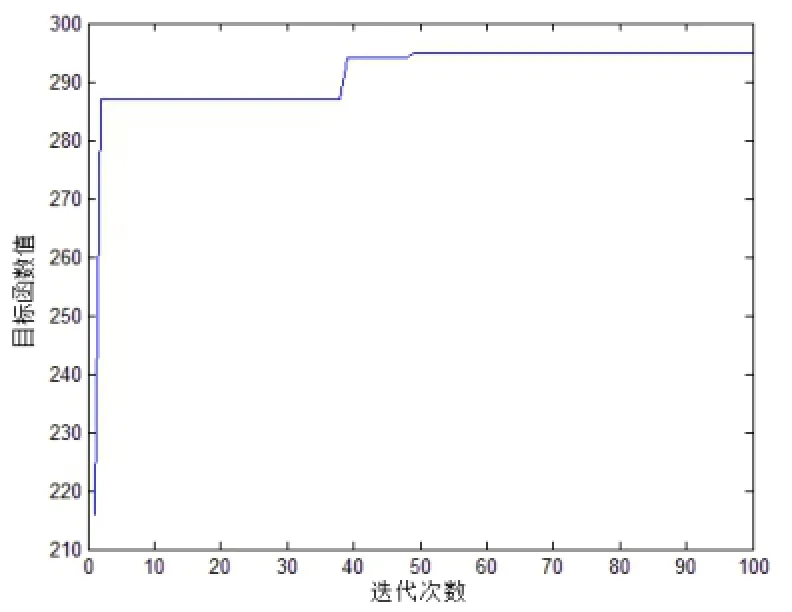
图1　算例2的优化示意图

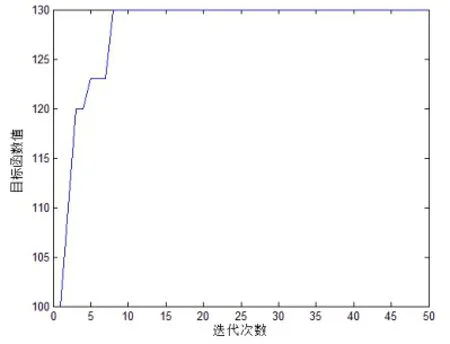
图2　算例2的优化示意图

为验证所提算法的优化性能，采用背包问题的典型算例进行实验。算法采用MATLAB（R2011a）软件编程实现，在CPU为i7、内存为4G的Dell台式机上运行。大量的数值实验表明，所提算法具有良好的优化性能。限于篇幅，仅给出其中2个算例。

算例1物品件数n=10，各个物品重量w=［95，4，60，32，23，72，80，62，65，46］，各个物品价值p=［55，10，47，5，4，50，8，61，85，87］，背包最大重量c=269，最优值为295。

算例2物品件数n=20，各个物品重量w= ［92，4，43，83，84，68，92，82，6，44，32，18，56，83，25，96，70，48，14，58］，各个物品价值 p=［44，46，90，72，91，40，75，35，8，54，78，40，77，15，61，17，75，29，75，63］，背包最大重量c=878，最优值为1024。

采用本文提出的布谷鸟搜索算法，对这2个算例进行求解，均可以获得最优解。图1-图2给出了算法的优化示意图。

本文提出的布谷鸟搜索算法在求解背包问题时表现出良好的优化性能，将算法用于其他类型的背包问题（如非线性背包问题、多维背包问题和多目标背包问题等）是进一步的研究方向。

［1］Yang X，Deb S.Cuckoo search via levy flights［C］.World Congress on Nature&Biologically Inspired Computing.Piscataway：IEEE Publications，2009：210-214.

［2］Yang X S，Deb S.Engineering optimization by cuckoo search［J］.International Journal of Mathematical Modeling and Numerical Optimization，2010，1（4）：330-343.

［3］樊小毛，马良．0-1背包问题的蜂群优化算法［J］.数学的实践与认识，2010，40（6）：155-160．

Knapsack Problem；Cuckoo Search Algorithm；Combinatorial Optimization

Cuckoo Search Algorithm for Solving Knapsack Problem

XU Qiu-yan
（School of Information Engineering，Yancheng Institute of Technology，Yancheng 224051）

1007-1423（2015）23-0032-03

10.3969/j.issn.1007-1423.2015.23.007

许秋艳（1981-），女，江苏东台人，硕士，讲师，研究方向为算法设计及其应用

2015-06-26

2015-08-05

背包问题是计算机科学一种典型的组合优化难题。为处理背包问题，设计基于布谷鸟搜索算法的优化方法。布谷鸟搜索算法是一种新型现代启发式算法，在求解连续优化问题时表现出良好的优化性能。在求解背包问题时，算法的搜索空间限制在连续空间，并通过自定义的映射，将背包问题的解空间和算法的搜索空间相对应。数值试验验证该算法的可行性和有效性。

背包问题；布谷鸟搜索算法；组合优化

Knapsack problem （KP）is a typical NP-hard problem in combinatorial optimization in computer science.To deal with KP，proposes a method based on cuckoo search algorithm（CSA）.CSA is a novel metaheuristic and shows good performance in solving continuous optimization problems.For solving KP，the search space of CSA is restricted in continuous space.The solution space of KP is corresponded to the search space of CSA by the self-defined map.The experimental results show that the proposed algorithm is feasible and effective.