面向无等待多目标柔性车间调度问题的遗传蜂群优化算法

毕孝儒，张黎黎，贺拴，贺艳果（四川外国语大学重庆南方翻译学院管理学院，重庆　401120）

面向无等待多目标柔性车间调度问题的遗传蜂群优化算法

毕孝儒，张黎黎，贺拴，贺艳果
（四川外国语大学重庆南方翻译学院管理学院，重庆401120）

0　引言

当前，无等待柔性车间调度问题 （No-Waiting Flexible Flow Job-Shop Scheduling Problem，NWFJSP）广泛存在于塑料塑造、钢铁铸造、化工制造等领域，它不仅需要确定工序的加工顺序，还要给每个工序分配机器，是更为复杂的NP-hard问题［1］。调度问题的复杂性，使得采用一般的数学规划方法很难求解因而许多学者运用遗传算法（Genetic Algorithm，GA）、粒子群算法（Particle Swarm Optimization，PSO）等智能优化算法［2-4］求解单目标NWFJSP问题，并取得了较好的效果。然而在实际生产中不仅要考虑工件最大完工时间、总拖延时间等调度性能指标，同时还要考虑生产成本等费用指标，即对多目标函数同时优化。因此求解多目标的无等待柔性车间调度问题更符合实际需求。

人工蜂群算法 （Artificial Bee Colony，ABC）是由Karaboga于2005年提出的一种群集智能优化算法。由于ABC算法具有收敛速度快、控制参数少，鲁棒性强等优点，一些学者［5］用其求解柔性车间调度问题。但该算法存在搜索后期容易陷入局部最优，且搜索速度慢的不足。

针对以上不足，本文给出了以关键路径为导向的变异操作，并将该变异操作和遗传算子中的IPOX和MPX交叉操作嵌入到人工蜂群算法中，以增强其全局寻优能力，提升搜索后期收敛速度，在设计了多目标优化模型和适应度值分配策略的基础上，将其用于无等待多目标柔性车间调度问题求解。

1　问题描述

无等待柔性车间调度问题可以描述为：设有m台机器和n个工件，pi表示工件i包含的工序数，Oijk表示工件工件i的第j道工序在机器k上加工，Sijk表示工序开始加工时间，Tijk表示工序的加工时间，每个工件包含一道或多道工序并且每道工序可以在多台性能不同的机器上加工，每道工序的加工时间、成本等因机器性能的不同而变化。调度目标是对所有工序在不同机器上的加工顺序进行排列，使总目标达到最优。同时加工过程还要满足以下假设和约束条件：

（1）在t=0时刻所有工件都可以被加工；

（2）所有工件的工序的先后顺序是固定不变的；

（3）同一时刻、同一台机器只能加工一道工序；

（4）同一工件工序之间有先后约束，上一工序r。

完成后才能开始下一工序r+1，即Si（r+1）k-Sirk-Tirk≧0。

本文针对无等待柔性车间调度的需求，给出了以下优化目标：缩短最大完工时间以增加生产效率、减少总拖延时间以提高客户满意度、减低成本以满足企业可持续发展，其需要优化的目标函数如下：

（1）最大完工时间

式中，Ti表示工件在机器i上的加工时间。

（2）生产成本

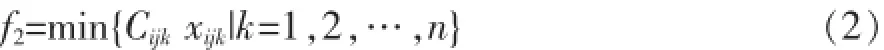
式中，Cijk表示工件i第j道工序在机器k上加工成本。

xijk决策变量，当工件Ji的第j道工序在机器k上加工时，xijk=1，否则为0。

（3）总拖延时间为：

式中，i=1，2，…，M，Ei表示工件i的最大完工时间，Di表示工件i的交货期。

2　灰互信息关联度适应度值分配策略

在多目标优化问题中，灰色关联度分析根据各目标的函数值组成数列的几何形状与参考序列接近程度来分析问题发展的态势。在优化时先将每个目标作为单目标分别求得最优解，并用这些最优解构成参考序列，即多目标优化的理想解。然后将Pareto解的目标函数值序列作为比较序列，利用灰关联度计算这两个序列的接近程度以分析每个Pareto解与理想解的近似程度，即利用灰关联度评判Pareto解的优劣。上述评判方法并未考虑个目标因素之间的信息，因而该分析方法的精度不高。本文将熵理论与灰色关联度分析结合，提出了灰互信息适应度值分配策略，其具体步骤如下：

（1）对于N个Pareto解，计算各目标函数值为：

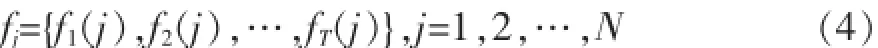
上式中，T为目标个数，fT（0）是第T个子目标作为单目标函数求出最优解的目标函数值，fi是每个子目标最优解组合而成的序列；

（2）依据式（5）对各Pareto解的目标函数值进行归一化处理；

其中，k=1，2，…，T，j=1，2，…，N。

3）依据式（6）计算各目标函数值之间的互信息量；

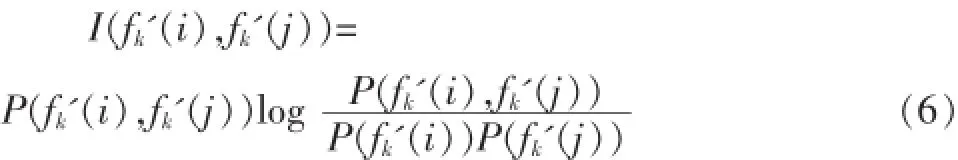
其中，P（fk'（i），fk'（j））为fk'（i），fk'（j）的联合熵。

（4）依据式（7）计算Pareto解灰互信息关联度；

其中，ρ∈（0，1）为分辨系数，一般取值为0.5。

3　遗传蜂群优化算法

3.1基本人工蜂群算法

在求解优化问题时，ABC算法将食物源位置抽象成优化问题的一个可行解，人工蜂寻找食物源的过程就是搜寻最优解的过程。人工蜂群主要包括雇佣蜂、观察蜂和侦查蜂三种个体。雇佣蜂数目和食物源数目相等，雇佣蜂和观察蜂各占蜂群总数的一半，食物源的含密量（收益度）对应优化问题的适应度函数。假设初始种群含有SN个解，每个解xi（i=1，2，…，SN）是一个d维向量。雇佣蜂首先寻找食物源，并根据式（9）进行食物源位置更新，

其中，k∈｛1，2，…，SN｝，j∈｛1，2，…，d｝，且k≠i。

雇佣蜂在进行位置更新后，若新食物源含密量高于旧食物源含密量时，用新位置代替原位置，否则仍保持对旧食物源的开采。

当雇佣蜂完成搜索后，观察蜂根据雇佣蜂传达的食物源信息，依照含密量以轮盘赌方式选择食物源：

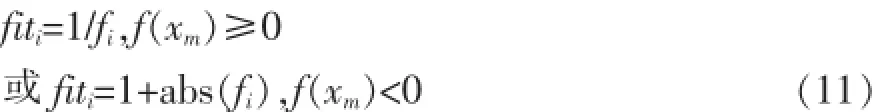
其中，Pi是第i个解的选择概率，fiti是第i个解的适应度值，fi是被优化问题的目标函数。在ABC算法中，如果某个解连续经过“limit”次循环后没有得到改善，则表明该解陷入局部最优，则此时与该解对应的雇佣蜂转变为侦查蜂，通过式（12）随机产生一个新解代替原解。

3.2遗传蜂群优化算法

作为模拟蜜蜂行为的一种新颖的群智能优化算法，人工蜂群算法具有简单、灵活、鲁棒性强、寻优时间短的优点，但其也存在全局搜索能力差，容易陷入局部最优的问题。遗传算法是一类模拟生物界自然选择遗传机制过程来解决负责问题的随机搜索算法，迭代计算过程从一组解（群体）出发，采用类似自然选择和游行繁殖的方式，通过交叉和变异操作，生成具有更好性能指标的下一代解的群体。遗传算法虽然有寻优时间长，搜索效率低的不足，但其具有较强的全局搜索能力。因而本文将遗传算子中的交叉和变异嵌入到人工蜂群算法中，提出了一种遗传蜂群智能优化算法。该算法描述如下：

输入：蜜蜂数量、变异概率、交叉概率；

输出：最优解及相应参数；

（1）依据式（12）随机生成对应蜜蜂数量的解（蜜源），利用式（7）求解适应度值；

（2）引领蜂在当前位置邻域内产生新位置，利用式（10）评价选择概率，在引领蜂搜索到的新位置和原位置中通过贪婪选择算子选取一个具有更高适应度的位置，保留给下一代种群；

（3）各跟随蜂按照式（10）选择跟随一个引领蜂，并在其邻域内进行新位置的搜索；

（4）当某只蜜蜂再起位置周围搜索次数达到某一阈值limit，仍没找到更优位置时，变为侦查蜂，并依据式（12）随机初始化其蜜源位置；

（5）按照交叉概率选择群体中的两个个体进行交叉操作 ，如果产生的新解优于父代，则替换父代，同时对最差个体按照变异率进行变异操作，变异后，若更好则替换最差个体；

（6）计算每个食物源适应度值及相应参数值；

（7）重复步骤（1）～（6），直到达到最大迭代次数。

4　求解NWMFJSP的遗传蜂群优化算法设计

4.1编码设计

针对无等待柔性车间调度不仅需要确定工序的加工顺序，还要给工序分配机器特点，本文采用一种扩展的基于工序编码，该编码由两部分组成：前半段是基于工序的编码，它是用来确定工序的加工顺序；后半部分是基于机器的编码，该编码中的机器按照每个工件工序的顺序进行排列，它用来给每个工序分配合适的机器。结合这两部分编码，就可以得到无等待柔性作业车间调度问题一个可行解。

4.2交叉

交叉操作是将种群中个体的某些基因随机交接，以产生新的基因组合。交叉的目的是将优良的基因进行组合以使子代较好地继承优良的父代基因。本文采用两种交叉操作［6］，第一种是改进工件优先顺序交叉（Improved Precedence Preserving Order-based Crossover，IPOX）用于染色体中加工工序的交叉；第二种是多点交叉操作（Multi-point Preservative Crossover，MPX）用于染色体工序分配的机器交叉。

（1）IPOX交叉

IPOX交叉是对每个个体中的工件顺序进行交叉，其具体操作过程是：所有的工件被随机分成两个集合J1，J2后，首先将父代染色体P1中包含在J1的工件复制到子代染色体C1，将父代染色体P2中包含在J2的工件复制到子代染色体C2，保留它们的位置不变，然后将父代染色体P1中包含在J1的工件复制到子代染色体C2，将父代染色体P2中包含在J2的工件复制到子代染色体C1，保留它们的顺序不变。图1给出了一个IPOX交叉示例，其中，J1=｛2，4｝，J2=｛1，3｝。

（2）MPX交叉

MPX交叉操作仅对染色体中工序分配的机器进行交叉。设父代染色体MP1和MP2，交叉产生的子代染色体分别是MC1和MC2，MPX交叉操作过程为：首先随机产生一个0、1组成的与染色体长度相等的序列集合R，其次将MP2和MP1中与R中的“1”的位置对应的工序选出，复制到MC1和MC2，最后将MP1和MP2中剩下的机器保留到MC1和MC2。

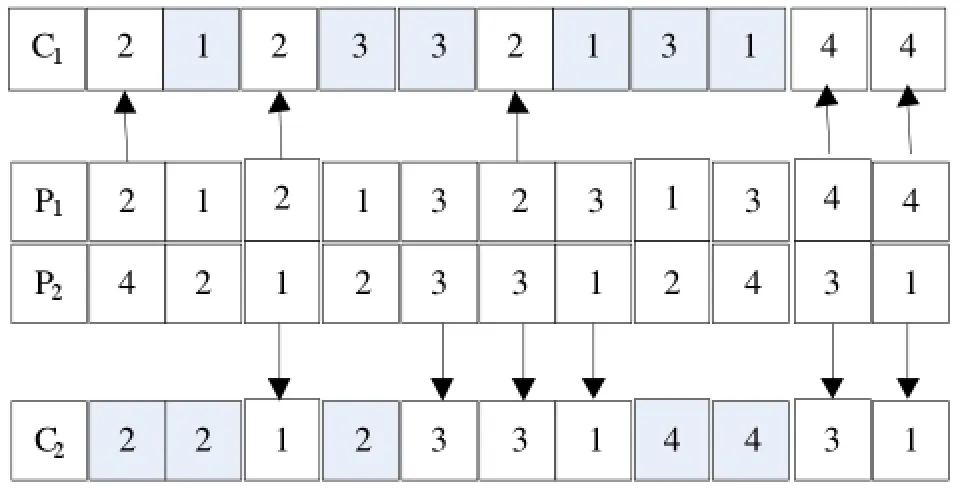
图1　IPOX交叉操作

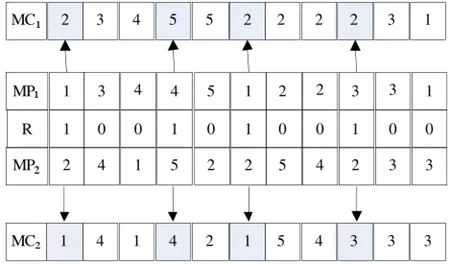
图2　MPX交叉操作

图2给出了一个MPX交叉示例，其中，1、2、3、4、5分别表示机器编号。

4.3以关键路径为导向的变异

引入变异算子是为了改善人工蜂群算法的局部搜索能力，有助于维持进化群体的多样性，防止过早陷入局部最优。考虑到无等待柔性车间调度具体问题，本文在变异中引入了关键路径的思想。

无等待柔性作业车间的可行调度可以通过有向图表示。在有向图从源点到汇点的路径中，长度最长的路径称为关键路径，且关键路径的长度等于无等待柔性作业车间的可行调度的最大完工时间。在关键路径上的所有工序都称为关键工序。任何一个关键工序一旦延迟，该调度的最大完工时间就必然会被推迟。图3为一无等待柔性车间调度示例的甘特图，其中，阴影工序为关键工序。

在变异过程中，只有当关键路径发生改变时，最大完工时间才会改变，才可能得到比父代更优的子代，因而本为给出了基于关键路径的变异操作。当对染色体的工序编码和机器分配编码进行变异时，分别通过改变关键路径上工序的顺序和修改关键工序所处的机器来达到改变关键路径的目的。

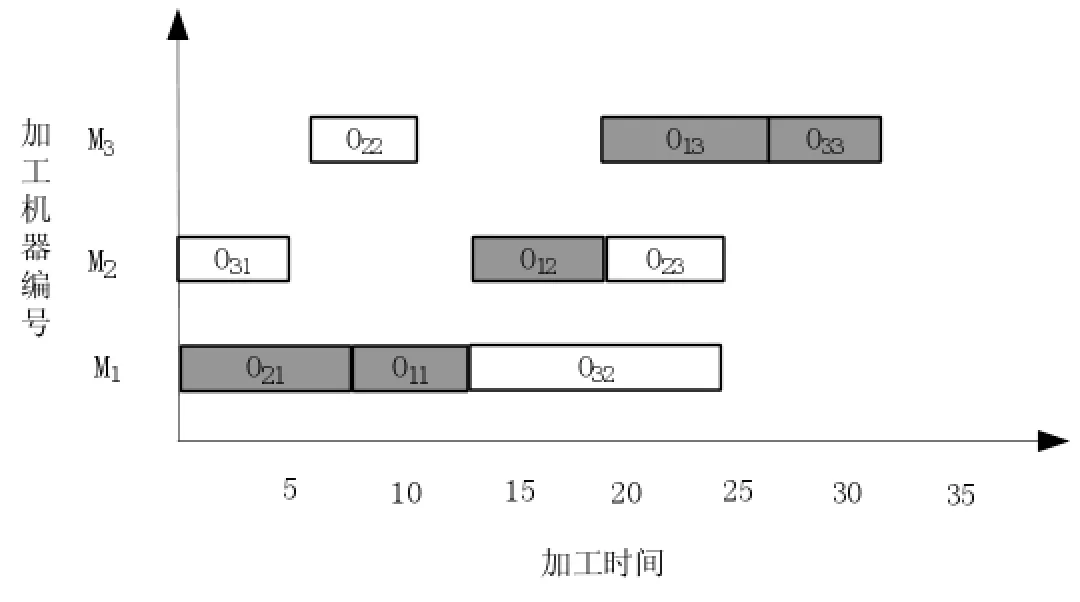
图3　甘特图示例

（1）基于工序编码的变异

对工序编码的变异，将变异位置的选择由整个染色体压缩到关键路径上。其操作过程为：从父代中随机选择一个关键工序，并且在满足工件内部顺序约束的前提下，将这个工序前插到其紧邻的前一个关键工序之前的某个位置，同时将对应的机器分配编码同步前移。图3对应的关键路径为｛O21，O11，O12，O13，O33｝，若选中关键工序O13，则其前插位置应在另一个关键工序O12之前，如图4所示。

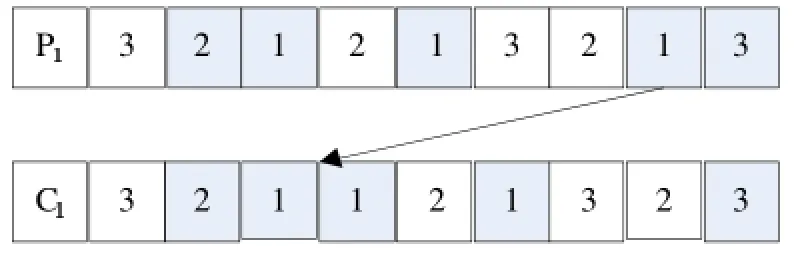
图4　基于工序编码的变异

（2）基于机器编码的变异

机器编码部分变异过程为：从加工成本最高的机器上选择一个关键工序，将它重新分配到加工成本最低的机器上。该变异过程不仅实现了对关键工序的修改，还实现了加工成本的降低。若图3中M2加工成本最高，M1的加工成本最小，则机器编码部分变异后结果如图5所示。

图5　基于机器编码的变异

5　仿真实验与分析

遗传蜂群优化算法在MATLAB 7.0上实现，实验采用文献［6］提供的实例数据进行测试。仿真硬件环境为Intel Core i5 CPU、2.2GHz主频、2GB内存；软件环境为Windows7操作系统。多目标混合人工蜂群算法参数设置为：种群规SN=50，采蜜蜂转成侦查蜂的limit= 6，最大迭代次数150。表2给出了遗传算法（GA）、人工蜂群算法（ABC）本文算法在三个目标函数函数上的平均值。三个优化目标的部分Pareto解集如表1所示，决策者可以根据企业实际，运用式（7）对Pareto解集各个解进行评价，并从中选出最优妥协解。图6是第16号解调度甘特图。

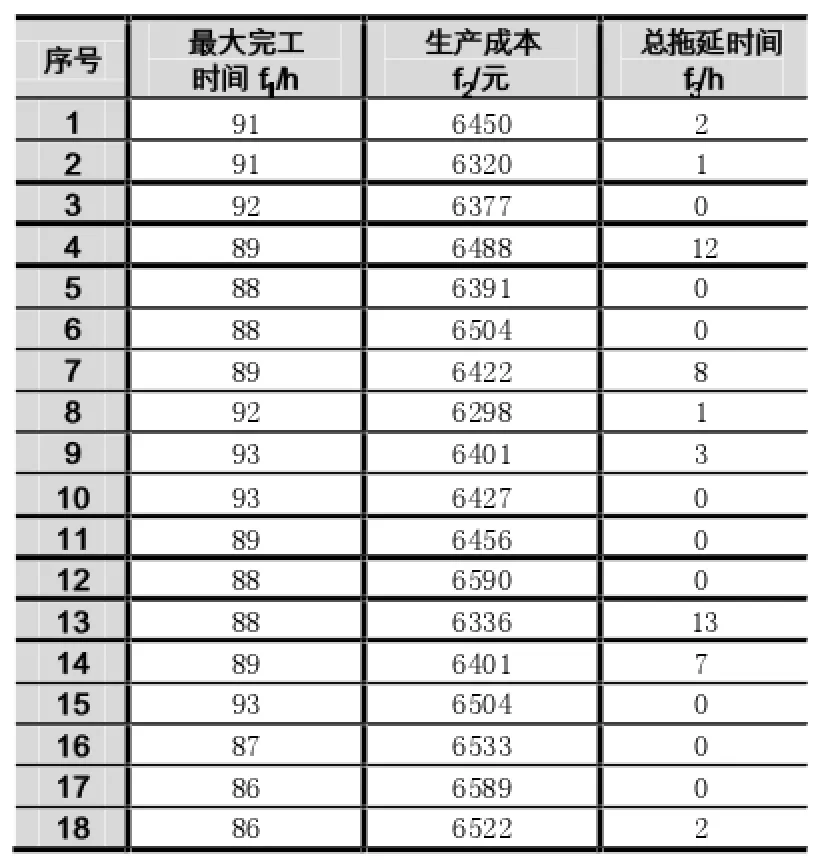
表1　部分Pareto解集

由表2中实验结果可知，本文提出的算法在求解无等待多目标柔性车间调度优化问题时在最大完工时间、生产成本、总拖延时间三个分目标上均具有一定优势。

表2　三种算法优化结果比较

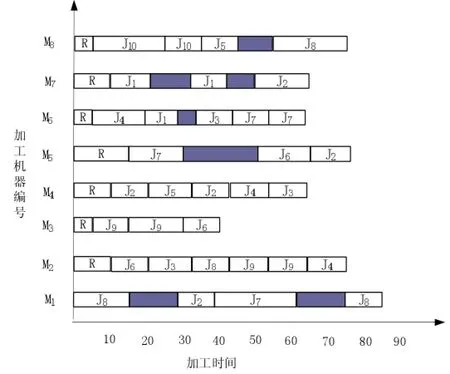
图6　第16号解的甘特图

6　结语

本文将最大完工时间、生产成本、总拖延时间作为为调度的目标函数建立了NWMFJSP的多目标调度模型，提出了灰互信息适应度值分配策略，给出了求解NWMFJSP问题的GABC算法。实验结果表明，提出的模型和算法对无等待多目标柔性车间调度问题是可行的。

［1］GAREY E L，JOHNSON D S，SETHI R.The complexity of flowshop and job-shop scheduling［J］.Mathematics of Operations Research，1976，1：117-129.

［2］Zhu Xia，Li Xiao-ping，Wang Qian.Total-idle-time increment based hybrid GA for no-wait flowshop with makespan minimization ［J］.Journal of Computer Research and Development，2011，48（3）：455-463.

［3］Zhou Hui-ren，Tang Wan-sheng，Wei Yinghui.PSO-based optimization of flexible flow-shop scheduling［J］.China Mechanical Engineering，2010，21（9）：1053-1056.

［4］基于混合粒子群-NEH算法求解无等待柔性流水车间调度问题［J］.系统工程理论与实践，2014，34（3）：802-809.

［5］混合蜂群算法求解柔性作业车间调度问题［J］.计算机集成制造系统，2011，17（7）.

［6］张超勇，董星，王晓娟等.基于改进非支配排序遗传算法的多目标柔性作业车间调度［J］.机械工程学报.2010，46（11）：156-164.

毕孝儒（1975-），硕士，网络工程师，研究方向为计算机网络安全与集成、智能优化

张黎黎（1982-），讲师，研究方向为软件理论与技术

贺拴（1982-），助教，研究方向为数据挖掘

贺艳果（1983-），助教，研究方向为教育学

NWFJSP；Multi-Objective Optimization GABC

Genetic Artificial Bee Colony Algorithm Faced with Multi-objective and No-wait Flexible Flow Job-shop Scheduling Problem

BI Xiao-ru，ZHANG Li-li，HE Shuan，HE Yan-guo
（School of Management，Chongqing South Translation College of University of SISU，Chongqing 401120）

1007-1423（2015）23-0011-06

10.3969/j.issn.1007-1423.2015.23.002

2015-06-04

2015-08-10

为了解决无等待柔性车间调度的多目标优化问题，构建以最大完工时间、生产成本、总拖延时间为目标函数的多目标调度模型，结合灰色关联分析和熵理论，提出灰互信息适应度值分配策略，以评价Pareto解的优劣。在此基础上，运用遗传蜂群优化算法求解，该算法给出以关键路径为导向的变异操作，并将该变异操作和遗传算子中的IPOX和MPX交叉操作嵌入到人工蜂群算法中，以增强其全局寻优能力，提升搜索后期收敛速度。一个车间调度实验验证调度模型和算法的有效性和适应性。

无等待柔性车间调度；多目标优化；遗传蜂群优化

四川外国语大学重庆南方翻译学院科研项目（No.ky2014004）

To solve no-wait and multi-objective flexible flow shop scheduling problem（NWMFJSP），proposes an optimization model，which takes finished time of maximum，machine cost and total delayed time as the objectives.Then presents the distribution strategy of the grey mutual information relational adaptive value combined with the grey correlation and information entropy to evaluate feasible solution.Based on it，applies genetic artificial bee colony algorithm（GABC）to solve the problem，the algorithm，which presents the mutation based on key path，embeds artificial bee colony with the nutation，IPOX and MPX crossover to enhance ability to search optimal solution globally and raise convergence rate in late search.The validity and adaptability of the scheduling structure and algorithm are proved by a case of job-shop scheduling.