饱和软粘土中新型法向承载力锚极限承载力分析

葛利忠　陆建辉

（中国海洋大学 工程学院 青岛266061）

饱和软粘土中新型法向承载力锚极限承载力分析

葛利忠陆建辉

（中国海洋大学 工程学院 青岛266061）

法向承力锚（VLA）因其安装回收方便、承载能力高、可重复使用等优点，被广泛应用于海洋工程。文中假设一楔形锚板埋置于理想不排水饱和软粘土中，通过建立锚板-土体有限元数值模型，对锚板的极限承载力和锚的失效形式进行分析，考察了不同埋深、埋置倾角等对其承载力系数的影响。在浅埋和深埋两种情况下，锚的失效形式分别表现为锚板上方土体的整体破坏和周边土体的局部剪切破坏。随着埋深增加，锚板承载力系数趋于稳定，埋置倾角对承载力系数的影响也逐渐变小。

楔形锚板；不排水饱和软粘土；极限承载力

引 言

拖曳式锚基础是目前海洋工程界深水锚泊系统的研究热点之一，其中的法向承力锚由于具有高承载力、安装回收方便以及可重复使用等优点，尤其适用于深水绷紧索系泊系统，因此此类锚基础在深水工程中正受到广泛关注。现场应用中，法向承力锚由锚体入水安装直到锚回收的整个过程中，存在诸如锚的准确定位、嵌入深度评估、运动轨迹描述、复杂环境中锚体工作状态及承载力分析等工程难题亟待解决。

目前国内外在锚的极限承载力分析方面，概括起来研究方法主要有三种：实验法、解析法、有限元数值模拟方法。

O’Neil（1997）等［1］通过离心机实验考察锚板和土的相互作用以及在嵌入过程中土体受力情况。荷兰Vryhof公司在巴西近海对法向承力锚做了小比尺实验，考察其工作性能和拖曳嵌入过程［2］。R.S.Merifield（2001）［3］利用上下限分析定理对不排水无重软粘土中水平和竖直埋设的条形锚板的承载力做了研究，其假设土体是理想的弹性材料并且服从Tresca屈服准则，得出在不同埋深下锚抗拔力系数的上下限值，并根据是否考虑土重，提出两种简便的锚板承载力系数计算方法。R.S.Merifield［4-6］还通过建立不同的模型研究条形锚板和圆形锚板的承载力状况，分析锚板在不同特性土壤中的极限承载力及锚失效时其周边土体的塑形流动机制。C.P.Aubeny（2010）［7］则通过建立垂直力V、切向力H、力矩M相关模型和不相关模型研究各承载力系数之间的关系，并分析软土海床中锚板形态如锚体长度、厚度、锚胫倾角等参数对承载力的影响。

O’Neil、M.F.Randolph（2003）等［8］利用有限元数值方法，分别建立条形和楔形锚板-土体模型，研究无重饱和软粘土中锚在拖拉过程中的受力特性，综合考虑力和力矩的影响，分析特定埋深下当位移方向与锚板上表面成特定夹角时，锚水平承载力和法向承载力之间的关系，还提出一种推测拖曳锚嵌入轨迹的计算方法。国内杨晓亮、刘君等［9-10］也分别建立二维、三维数值模型，对条形和圆形锚板的极限承载力进行研究；王晖等［11］则利用有限元模型研究不同土质、不同锚板粗糙度等对极限承载力的影响。

本文利用有限元数值方法， 参考O’Neil （2003）［8］对锚的分析描述，将法向承力锚简化成一楔形锚板，建立锚-土二维有限元数值模型，分析锚板在浅埋和深埋情况下锚的失效形式，研究不同的埋深、埋置倾角对承载力的影响，并将所得结果与其他分析实验数据进行比较。

1　数值分析模型的建立

1.1VLA工作状态分析

图1表示的是法向承力锚在工作状态下的受力情况。从图中可以看出，锚板在土中的嵌入角度为α ，Fa表示系缆作用在锚杆上的拉力，拉力方向与水平方向的夹角为β；FV表示锚板所承受的法向压力，包含了锚板上土体压力，锚板下表面吸附力，锚杆及锚板上摩擦力的法向分力，锚板自身重力法向分力；FH表示锚板所承受的平行于锚板上表面的外力，包含有锚板和锚杆摩擦力沿锚板上表面方向的分力，锚板自身重力锚板方向分力；M为锚板上的力矩，本文分析中，假设锚板上不存在力矩作用。

图1　工作状态下锚的受力

图2是锚板在土中的埋设状态。图中，B为锚板长度，d为锚板最宽处长度，H表示锚板埋设深度，锚板上的法向拉力为F。锚板在土中的埋设角度分为0°、22.5°、45°、67.5°、90°五种情况。

图2　锚在海底土中的埋设情况及受力状态

1.2建立有限元数值模型

根据相关资料和R.S.Merifield（2001）［5］、O’Neil（2003）［9］等人的研究成果，对土体作如下描述：假设土体是无重不排水饱和软粘土，理想弹塑形材料，满足摩尔-库伦屈服准则。土体不排水抗剪强度与埋深的关系为：Sμ=1.5H，土体弹性模量E与不排水抗剪强度Sμ之比为500，即E/Sμ=500，泊松比为0.49。锚板弹性模量为2.1E11，泊松比为0.3，锚板表面极其粗糙。根据M.F.Randolph （2003）［8］、王晖［11］等人研究表明当法向位移载荷从0逐渐达到0.2 m 过程中，VLA极限承载力逐渐变大并趋于稳定状态，本计算中取位移载荷s=0.2 m，利用有限元分析中典型的增量迭代法，将位移载荷分步施加并求解。

本文利用有限元分析软件ABAQUS进行建模分析，其具有优越的非线性分析功能以及Mohr-Coulomb模型、Drucker-Prager模型等多种模型可用来模拟土体分析，网格划分采用四边形平面应变单元（CPE4R），数值模拟过程采用减缩积分方法。

建立二维有限元数值模型如图3，土体尺寸为60 m×60 m，锚板尺寸B=3.5 m，d=0.5 m，（根据M.P. O’Neill［9］的研究，这种后角为45°，前面9.5°的楔形结构，形状上更加接近某款Stev式法向承力锚）。对土体下表面施加竖向约束，左右表面施加水平约束，锚板上表面施加法向位移载荷。锚板与土体之间进行接触处理，设定锚板表面为主动面，土体接触面为从动面，锚板与土体之间受力可分离。

图3　锚-土有限元模型

2　计算结果分析

2.1锚板周围土体流动及破坏机制

图4中列举的是H/D=2、H/D=6、H/D=10三种情况下，当锚板达到极限承载力时，锚周边土体的位移流动变化以及土体的塑性变形应变。从中可以看出当锚埋设较浅时，土体的破坏线从锚周围延伸到土体上表面，海底土表面隆起，此时锚的失效表现为土的完全破坏，锚从土体中拉出；当锚处于深埋时，土体流动曲线包络锚板四周，主要集中于锚板上方和左右两端，这说明土体发生局部破坏，锚已失效，此时的破坏形式表现为锚周边土体的塑性流动。同时这组结果图片也反映了随着深度的增加，尤其在深埋情况下，土的破坏模式逐渐变为局部剪切破坏和土的塑性流动，即锚的极限承载力变化模式趋于稳定。

图4　数值模拟土体流动及塑性应变图

图5（a）是O’Neil、M.F.Randolph（2003）等［9］通过建立有限元数值模型对条形锚板分析所得到的土体破坏塑性流动图，图5（b）图反映的是上限定理分析下条形锚板周围土体流动规律。比较图4、图5两组图片，锚板上表面土体流动模式十分吻合，而锚板下方土体流动变化却有差异，这也说明：不同形状的锚板在失效破坏时，周围土体塑性流动有所不同。同时这种流动的相似性，也反映在相同条件下，锚板失效产生位移之后，形状的不同对极限承载力的影响有限，因为此时锚板下表面与土体已分离，所以结果的差异可看作锚在移动中侧面摩擦的影响。

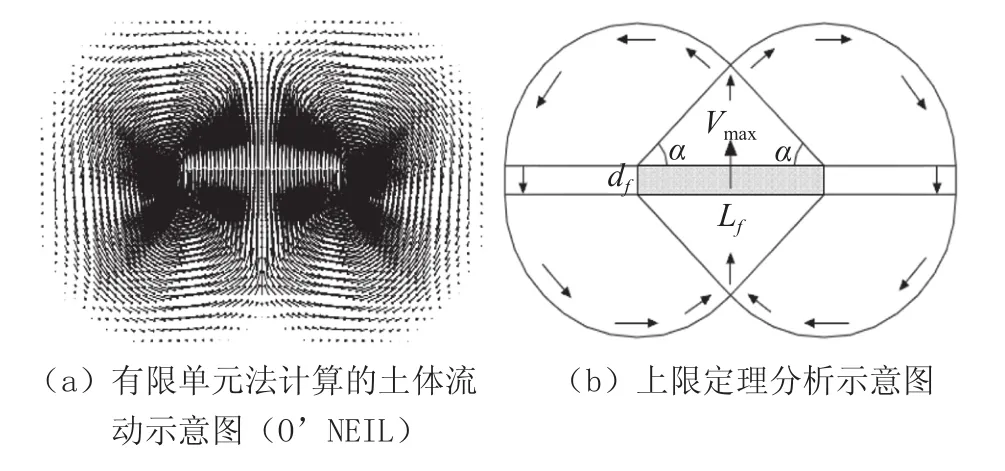
图5　其他理论下土体破坏流动图

2.2锚板极限承载力

利用位移控制方法进行加载，通过得到VLA承载力与锚体位移荷载的关系曲线，再确定相应的极限承载力。典型的弹塑性荷载曲线包含弹性段、过渡段和塑性段（塑性破坏区）。当位移荷载达到一定程度后（如图6中S3点），VLA承载力将保持不变，但位移荷载继续增加，锚板周围土体将形成贯通破坏，甚至有的锚体承载力会有所降低。因此本文中将锚体承载力-位移荷载曲线中的S3点所对应的荷载作为锚板的极限抗拔力。

目前工程中对锚板极限承载力一般采用经验公式进行估算：

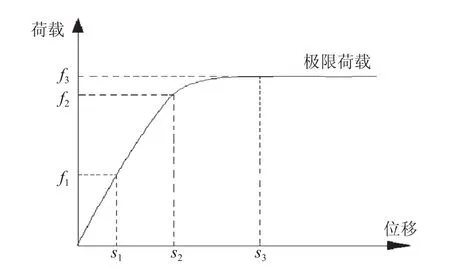
图6　锚板承载力-位移关系图

式中：NC为承载力系数；F为极限承载力；A为锚板上表面面积；Sμ为不排水抗剪强度。

R.S.MERIFIELD（2001）［5］针对承载力系数提出一组简单方便的计算公式，其中γ为单位土重。

（1）当土体为匀质无重土时，公式如下：

（2）当土体匀质但考虑土重影响时，公式如下：

对于承载力系数的取值，目前尚未有定论，O’NEIL（2003）［9］在土体周边全约束下得出无重土中楔形锚板法向承载力系数为11.53，R.S. MERIFIELD（2001）［5］利用上下限定理计算得到无重土中条形锚板承载力系数为6～9之间。查阅相关国内外资料和实验数据，承载力系数在6～14之间。

利用文中公式（1），代入模拟所得到的极限承载力，便得到承载力系数。图7表示本文中承载力系数值分析结果。根据曲线规律当埋深较浅时，所得承载力系数与R.S.MERIFIELD（2001）［5］利用上限定理所求的结果比较吻合，随着埋深的增加，本文承载力系数数值计算结果逐渐倾向于上下限定理所得结果之间，并逐渐趋于稳定。

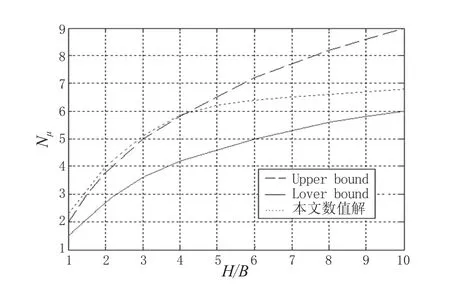
图7　承载力系数曲线

2.3埋设角度的影响

图8反映了承载力系数随埋设角度变化的曲线。从中可看出：在不同埋深下，埋设角度对法向承载力的影响，随着埋深的增加，承载力系数曲线趋于平缓，即不再随着埋设角度的变化而改变；当锚板浅埋时，竖直埋设水平受力的情况下，承载力最大；在同一倾角下，埋深越大，承载力系数越大；图片曲线也显示，在倾斜角度小于45°时，承载力系数变化较小，当倾斜角度在45°～ 90°时，承载力系数变化较大。

图8　承载力系数随埋设角度变化曲线

3　结 论

本文利用有限元方法通过建立数值模型，对楔形锚板进行模拟分析，得出以下结论：

（1） 不同埋深下锚的失效破坏表现形式不同，浅埋时锚板周围土体发生整体破坏，锚从土中被拉出；深埋时锚周围土体发生局部剪切破坏，土体产生局部流动。

（2） 在假设无重土的前提下，所得锚的承载力系数小于上限解，但仍大于下限解。此前提忽略了锚板自身重力和上覆土压力，这是造成结果偏小的主要原因。

（3） 埋设角度只有在浅埋时对锚板的法向承载能力有较大影响，随着埋深的增加这种影响逐渐变小，本文结果中当H/D=10时，承载力系数基本不再变化。

（4） 在浅埋下锚板竖直埋设相比于水平埋设，能承受更大的法向拉力。

［ 1 ］ O’Neill M P，Randolph M F，Neubecker S R. A novel procedure for testing model drag anchors［A］. Proceedings of the 7thInternational Offshore and Polar Engineering Conference［C］//Honolulu，Hawaii，1997：939-945.

［ 2 ］ Vryhof Anchors. Anchor Manual 2005［M］. Krimpen，ad YJssel， The Netherlands.

［ 3 ］ Merifield R S，Sloan S W，Yu H S．Stability of plate anchors in undrained clay［J］．Geotechnique，2001（2）：141-153.

［ 4 ］ Merifield R S， Lyamin A V， Sloan S W. Threedimensional lower bound solutions for stability of plate anchors in clay［J］. Journal of Geotechnical and Geoenvironmental Engineering， 2003，129：243-253.

［ 5 ］ Merifield R S， Lyamin A V，Sloan S W. Stability of inclined strip anchors in purely cohesive soil ［J］. Journal of Geotechnical and Geoenvironmental Engineering， 2005（3）： 792-799.

［ 6 ］ Merifield R S，Sloan S W. The ultimate pullout capacity of anchors in frictional soils［J］. Geotechnique，2006，43：852-868.

［ 7 ］ Aubeny C P， Chi C. Mechanics of drag embedment anchors in a soft seabed［J］. Journal of Geotechnical and Geoenvironmental Engineering， 2010（1）： 57-68.

［ 8 ］ O’Neill M P， Bransby M F， Randolph M F. Drag anchor fluke-soil interaction in clays［J］. Canadian Geotechnical Journal， 2003，40：78-94.

［ 9 ］ 刘海笑，杨晓亮. 法向承力锚极限抗拔力特性［J］.海洋工程，2006（4）： 8-14 .

［10］ 刘君，于龙，吴利玲，等. 饱和黏土中倾斜圆形锚板承载力分析［J］. 大连理工大学学报，2008（2）：229-234.

［11］ 王晖，董玉才，李新超，等. 法向承力锚极限抗拔力影响因素的二维有限元分析［J］. 天津大学学报，2010（11）：964-970.

［12］ Merifield R S，Lyamin A V，Sloan S W. Stability of inclined strip anchors in purely cohesive soil ［J］. Journal of Geotechnical and Geoenvironmental Engineering， 2005（3）： 792-799.

Analysis of ultimate bearing capacity for new-type vertically loaded anchor in saturated soft clay

GE Li-zhong LU Jian-hui
(Engineering College , Ocean University of China , Qingdao 266061, China)

The Vertically Loaded Anchor (VLA) is widely applied in ocean engineering due to the convenient installation and recycling, high bearing capacity and reusability. It is assumed that a wedge-shaped anchor is buried in the ideal undrained saturated soft clay. A finite element modeling of anchor-soil has been established to carry out the analysis of the ultimate bearing capacity and the failure pattern of the anchor, and the investigation of the influence of different embedment depths and angles to the bearing capacity factor. It is found that the failure pattern shows a whole damage of soil above the anchor for the shallow embedding, and a local shear damage of the surrounding soil for the deep embedding, respectively. With the increasing embedment depths, the bearing capacity factor of the anchor tends to be stable, and the influence of embedment angles on the bearing capacity factor becomes smaller and smaller.

wedge-shaped anchor; undrained saturated soft clay; ultimate bearing capacity

TU312

A

1001-9855（2015）02-0052-05

2014-12-22；

2015-01-29

葛利忠（1986-），男，硕士，研究方向：海洋机电装备与仪器。陆建辉（1960-），男，博士，教授，研究方向：海洋结构设计与动力分析。