UPFC附加阻尼控制器设计研究

宋鹏程，甄宏宁，王震泉，徐　政，董桓锋

UPFC附加阻尼控制器设计研究

宋鹏程1，甄宏宁2，王震泉2，徐政1，董桓锋1

（1.浙江大学电气工程学院，浙江杭州310027；2.江苏省电力设计院，江苏南京211102）

提出一种基于测试信号法的统一潮流控制器（UPFC）附加阻尼控制器设计方法。首先运用测试信号法进行系统小信号稳定性分析；然后运用测试信号法求得从UPFC有功功率指令值到并联交流联络线有功功率的开环传递函数；最后基于经典控制理论的极点配置算法便可整定UPFC附加阻尼控制器的各个参数。利用PSS/E验证了所设计的UPFC附加阻尼控制器的有效性。以南京西环网系统为例，验证所提出的UPFC附加阻尼控制器设计方法在实际电力系统中应用的有效性。

UPFC；附加阻尼控制器；测试信号法；参数整定方法

随着电网规模的急剧增长，负荷水平的持续攀升，远距离大功率互联的工程实例越来越多。区域间的低频振荡成为限制区域联络线输电能力，甚至影响互联电网安全稳定运行的主要因素之一。柔性交流输电（FACTS）技术的出现为抑制低频振荡，特别是区域间振荡提供了新的手段［1-3］。作为最新一代的FACTS装置，统一潮流控制器（UPFC）能够实现潮流的精确控制，对电网动态稳定性和电压稳定性均有较大影响。通过加装UPFC附加阻尼控制器，能够提高系统阻尼比，抑制系统低频振荡［4-6］。控制器的参数整定是UPFC附加阻尼控制器设计的核心问题之一。近年来，常见的控制器设计方法包括遗传算法、进化策略、模糊控制等［7-10］，然而实际大系统中状态方程异常繁杂，使用上述方法整定UPFC附加阻尼控制器参数存在一定的困难。

本文首先提出了一种UPFC附加阻尼控制器的设计方法，采用测试信号法和极点配置法对UPFC附加阻尼控制器的参数进行整定，从而在整定过程中避开在常规设计中遇到的困难、便于实际工程应用；然后在PSS/E中验证了所设计的UPFC附加阻尼控制器的有效性；以南京西环网系统为例，验证所提出的UPFC阻尼控制器设计方法在实际电力系统中应用的有效性。

1　基于测试信号的UPFC附加阻尼控制器设计

1.1UPFC附加阻尼控制器结构

UPFC抑制低频振荡的作用主要通过UPFC附加阻尼控制器实现，UPFC附加阻尼控制器的基本结构如图1所示，具有类似于电力系统稳定器的结构。一般它的传递函数由以下4部分构成：稳定信号隔直，相位超前补偿，稳定器增益和稳定器限幅环节。

（1）稳定信号隔直。隔直环节与PSS中的隔直环节的作用相同，为一高通滤波器。其主要作用是避免故障后UPFC控制输入信号中可能存在的直流分量对UPFC附加阻尼控制的影响。

（2）移相环节。移相环节是阻尼控制中的主要环节，其作用是使UPFC的输出随着输入信号的变化而产生一个与输入信号之间相位差，这就需要相位超前回路，以补偿UPFC阻尼控制器输出与形成的电气转矩之间的相位滞后，从而有效阻尼系统低频振荡。

（3）控制器的增益。控制器的增益对阻尼系统振荡有重要作用，它的大小决定控制器向系统提供阻尼的大小。UPFC附加阻尼控制器的基本机构如图1所示。x为附加阻尼控制器的输入信号，一般可以取联络线功率波动、发电机转速、系统频率等作为附加阻尼控制器的输入信号。附加阻尼控制器产生的输出信号与UPFC有功功率指令值叠加后一起作为UPFC潮流控制器的输入信号。

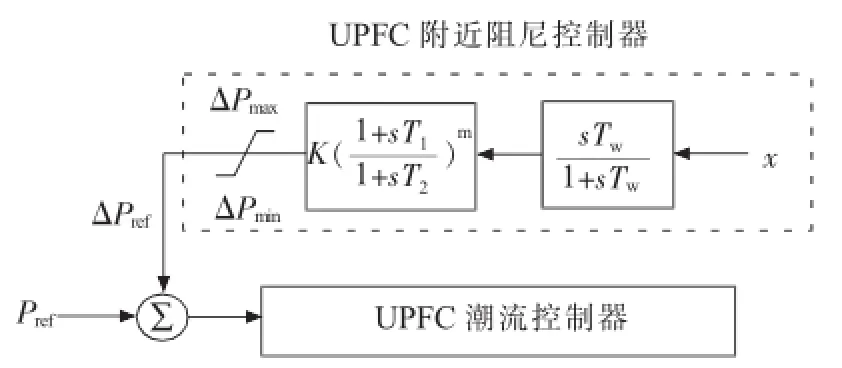
图1　UPFC附加阻尼控制器的基本结构

1.2UPFC附加阻尼控制器参数整定方法

选择交流联络线功率波动作为UPFC附加阻尼控制器的输入信号，从并联交流联络线上提取反映交流联络线路功率波动的信号，来调节UPFC控制线路传输的功率，使之快速吸收或补偿交流联络线路的功率过剩或缺额，起到阻尼振荡的作用。以UPFC有功功率指令值增量ΔPref作为控制变量，交流联络线输送有功功率增量ΔPac作为被控变量，则ΔPref到ΔPac的开环传递函数框图如图2（a）所示。引入ΔPac作为反馈变量，系统的闭环传递函数框图如图2（b）所示。

图2　系统传递函数

系统闭环传递函数为：

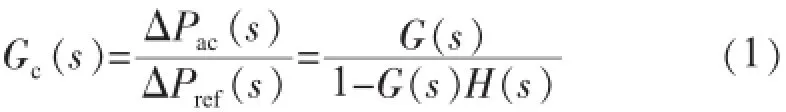
式（1）中：G（s）为系统开环传递函数；H（s）为反馈信号传递函数。

由式（1）可得闭环系统的特征方程为：

假设加入反馈补偿环节后闭环系统新的主导极点为sd，sd必满足系统特征方程，可得：

分别写成幅值和相角的形式：

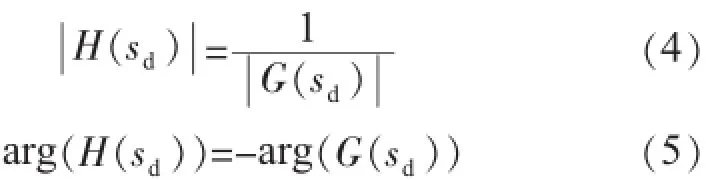
因此，反馈补偿环节H（s）在s=sd处的幅值和相角可以通过系统开环传递函数G（s）在s=sd处的幅值和相角求得。根据所得结果，可设计超前—滞后补偿环节并整定相应参数。

图1所示附加控制器对应的传递函数形式为：

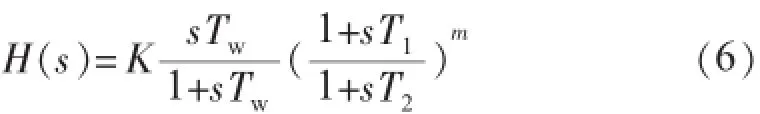
可设计超前—滞后补偿环节的参数为［2］：

式（7）中：φ为需要补偿的相位；arg（G（sd））为开环传递函数在期望主导极点处的相位；ωk为期望主导极点的虚部；m为相位补偿环节阶数，本文取3。

确定T1，T2后，可以通过式（4）来确定增益K。

1.3基于测试信号法的系统传递函数辨识

由以上分析可得，设计超前—滞后补偿UPFC附加控制器的关键是求取从UPFC有功功率指令值到并联交流联络线有功功率的开环传递函数。在实际大系统中用解析法求这一开环传递函数非常困难，但利用

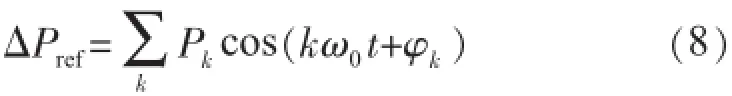
式（8）中：kω0=0.1～2.0 Hz；Pk，φk分别为相应振荡电流的幅值和相位。对所加ΔPref的要求是不能破坏系统线性化条件。

由于系统在运行点附近基本上是线性的，不同频率的量不会相互干扰。因此可以一次施加多个不同频率的干扰电流信号。

（2）对系统进行机电暂态仿真直到稳态，并提取公共周期内的数据量ΔPref和ΔPac。

（3）对ΔPref和ΔPac做傅立叶分解，得到不同频率下的相量（kω0）和ΔP.ac（kω0）。

（4）对所有的kω0计算不同频率下的传递函数：

（5）利用数据拟合辨识出的表达式。在求得开环传递函数的解析表达式后，可进行UPFC附加阻尼控制器参数整定。

1.4UPFC附加阻尼控制器设计步骤

（1）用测试信号法对交直流系统进行小信号稳定性分析，求出系统主要振荡模式的频率和阻尼比。

（2）根据（1）的结果选择期望的主导极点。

（3）用测试信号法辨识从UPFC有功功率指令值到并联交流联络线有功功率的开环传递函数G（s）。

（4）根据（3）求出相应于期望主导极点的UPFC附加阻尼控制器的补偿相位和幅值，采用极点配置法整定UPFC附加阻尼控制器的参数。

（5）应用测试信号法重新计算系统主要振荡模式的频率和阻尼比。

2　算例

算例系统是如图3所示的一个简单的电力系统，UPFC装置安装在节点7与节点9之间的一回线路上，将线路功率控制在2.2+j0.0。

用测试信号法分析系统主要振荡模式的频率和阻尼比，结果如表1所示。

由表1可以看出，系统中存在一个阻尼比极低的测试信号法可以方便地做到。测试信号法基于频率响应和模态辨识理论［11］。对于任何一个线性系统，施加的动态输入将会激发出相应的动态输出响应。这些输入激励和输出响应之间存在一定的因果关系，即为线性系统的动态特性。电力系统是一个非线性系统，但当系统遭受小扰动时，可将系统在工作点附近线性化，因此传递函数的求取可用测试信号法。

（1）在UPFC有功功率指令值上施加一系列小信号振荡功率，即：振荡模式（振荡模式1），可以通过加装UPFC附加阻尼控制器提高振荡模式1的阻尼比，改善系统动态特性。附加阻尼控制器的输入信号为7-8一回线路的有功功率。用测试信号法辨识从UPFC有功功率指令值到并联交流联络线有功功率的开环传递函数G（s）。通过时域仿真得到G（s）的幅频特性，通过模态辨识可得到G（s）的表达式为：

图3　算例系统示意图

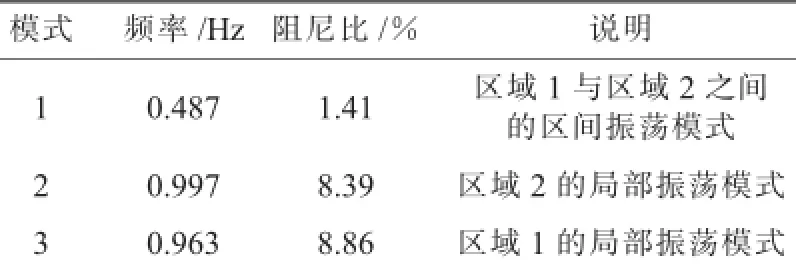
表1　加装UPFC附加阻尼控制器前系统主要振荡模式

UPFC附加阻尼控制器的目标是将与振荡模式1对应的主导极点的阻尼比提高到20%。因此将期望的主导极点sd设置在-0.63+j3.1，对应振荡频率为0.5 Hz，阻尼比为20%。使用UPFC附加阻尼控制器参数整定方法得到UPFC附加阻尼控制器的参数：K= 0.107，Tw=10.0 s，T1=0.55 s，T2=0.20 s，限幅为±25 MW。加入UPFC附加阻尼控制器后，再用测试信号法分析系统低频振荡特性，测试结果如表2所示。UPFC附加阻尼控制器安装前后系统在大扰动下的动态特性如图4所示，图4中曲线为大扰动下7-8一回线路的有功功率。具体仿真过程：2 s时发电机G3出口处发生三相接地故障，2.1 s故障切除。

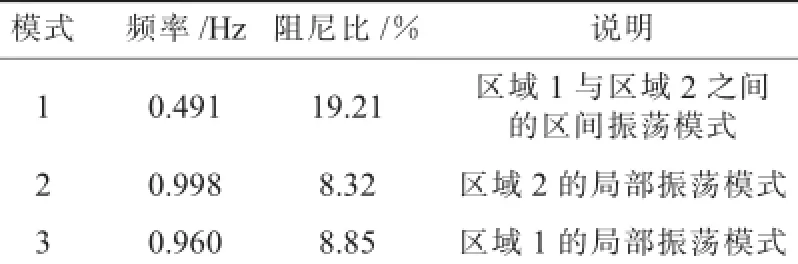
表2　加装UPFC附加阻尼控制器后系统主要振荡模式

由表1和表2可以看出，设计的UPFC附加阻尼控制器具有良好的阻尼效果，设计的UPFC附加阻尼控制器将振荡模式1的阻尼比从1.41%提升至了19.21%，而对区域1和区域2内的局部振荡模式基本没有影响。由图4可以看出，加装UPFC附加阻尼控制器后，系统在遭受大扰动时能够迅速的平息振荡，具有较好的动态特性。验证了所提出的UPFC附加阻尼控制器设计方法的有效性。

为验证所设计的UPFC附加阻尼控制器的适应性，在几个不同工况下加装UPFC附加阻尼控制器。工况1为设计UPFC附加阻尼控制器时考虑的工况，线路7-9的功率被控制在2.2+j0.0；工况2中将线路7-9的功率控制在1.5+j0.0；工况3中将线路7-9的功率控制在2.9+j0.0；工况4中将线路7-9的功率控制在3.6+j0.0。加装的UPFC附加阻尼控制器参数为工况1下设计得到的UPFC附加阻尼控制器参数。加装UPFC附加阻尼控制器后不同工况下振荡模式1的频率和阻尼比如表3所示。

图4　并联交流联络线7-8一回线路的有功功率

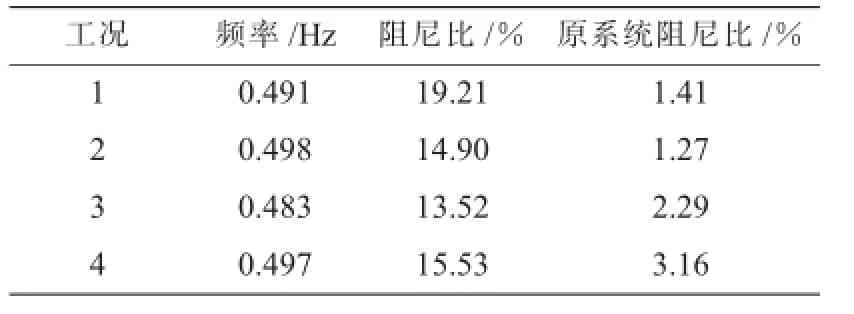
表3　加装UPFC附加阻尼控制器后不同工况下振荡模式1的频率和阻尼比

由表3数据可以看出，设计的UPFC附加阻尼控制器对不同的运行工况具有较好的适应性。

3　实际电力系统应用验证

以南京西环网系统为例验证所提出的UPFC阻尼控制器设计方法在实际电力系统中应用的有效性。南京西环网系统接线示意图如图5所示。UPFC装置加装在铁北—晓庄双回线路上［12］。UPFC装置投运后，南京西环网系统中存在一个频率为1.422 Hz，阻尼比为7.15%的振荡模式，主要表现为苏华润机组对苏镇厂机组的区间振荡。针对此振荡模式，利用UPFC附加阻尼控制器设计方法，设计UPFC附加阻尼控制器。附加阻尼控制器的输入信号为秦淮—滨南一回线路的有功功率，整定得到的控制器参数为：K=0.021，Tw=10.0 s，T1=0.55 s，T2=0.08 s，限幅为±25 MW。

分析加装UPFC附加阻尼控制器后南京西环网系统的低频振荡特性发现，安装UPFC附加阻尼控制器后，苏华润机组对苏镇厂机组振荡模式的阻尼比从7.15%提升至了11.06%。UPFC附加阻尼控制器安装前后南京西环网系统在大扰动下的动态特性如图6所示。图6中曲线为大扰动下苏华润机组的转速差曲线。具体仿真过程：1 s时晓庄—下关线路发生三相接地的故障，UPFC退出运行；1.1 s故障切除；为保证UPFC装置安全，经过设定时间（1 s）后，2.1 s时UPFC重新投入。

图5　南京西环网系统接线示意图

图6　苏华润机组的转速差曲线

由图6可以看出，UPFC附加阻尼控制器加装前，南京西环网系统已经具有比较理想的动态特性，加装UPFC附加阻尼控制器可以进一步改善南京西环网系统的动态稳定特性，进一步增加系统的阻尼比，加快振荡的平息过程。且UPFC附加阻尼控制器设计方法在实际电力系统中的仍然有效。

4　结束语

本文提出了一种UPFC附加阻尼控制器的设计方法，采用测试信号法和极点配置法对UPFC附加阻尼控制器的参数进行整定，从而在整定过程中避开在常规设计中遇到的困难、便于实际工程应用。首先运用测试信号法进行系统小信号稳定性分析；然后运用测试信号法求得从UPFC有功功率指令值到并联交流联络线有功功率的开环传递函数；最后基于经典控制理论的极点配置算法便可整定UPFC附加阻尼控制器的各个参数。UPFC附加阻尼控制器设计方法简单、易行，即使考虑复杂的发电机模型及励磁和调速器模型时，也不增加整定过程的复杂度，使用常规机电暂态仿真程序便可实现。UPFC附加阻尼控制器设计方法的有效性在简单算例系统与实际电力系统中均得到了验证，对南京西环网UPFC工程投运后系统动态稳定特性的改善具有重要作用。

［1］林宇锋，徐政，黄莹.TCSC低频振荡阻尼控制器设计研究［J］.电网技术，2005，29（22）：34-39.

［2］常勇，徐政.SVC广域辅助控制阻尼区域间低频振荡［J］.电工技术学报，2006（12）：40-46.

［3］SANCHEZ GASCA J J.Coordinated Control of two FACTS Devices for Damping Interarea Oscillations［J］.IEEE Trans.on Power Systems，1998，13（2）：428-434.

［4］胡晓波，陈中，杜文娟，等.利用多端统一潮流控制器阻尼多模态振荡［J］.电力系统自动化，2007（17）：35-39.

［5］刘青，马朋，邹家平.基于WAMS的UPFC装置的附加控制器设计［J］.华北电力技术，2015（2）：13-18.

［6］TAMBEY N，KOTHARI M L.Damping of Power System Oscillations with Unified Power Flow Controller（UPFC）［C］.IEE ProceedingsonGeneration，TransmissionandDistribution，2003（150）：129-140.

［7］周前，方万良.基于TCSC技术和粒子群优化算法的电力系统阻塞疏导方法［J］.电网技术，2008，32（8）：47-52.

［8］郭成，李群湛.基于改进PSO算法的SSSC广域阻尼控制器设计［J］.电工技术学报，2010（25）：151-157.

［9］牛振勇，杜正春，方万良.基于进化策略的多机系统PSS参数优化［J］.中国电机工程学报，2004，24（2）：22-27.

［10］ASADI M R，SADR V G.UPFC Online PI Controller Design Using Particle Swarm Optimization Algorithm and Artificial Neural Networks［C］.Proceedings of 2th IEEE International Conference on Power and Energy，Johor Baharu，2008：473-478.

［11］XU Z，FENG Z.A Novel Unified Approach for Analyzing Smallsignal Stability of Power Systems［C］.Power Engineering Society Winter Meeting.Jan.22-27，2000，Singapore.

［12］蔡晖，祁万春，黄俊辉，等.统一潮流控制器在南京西环网的应用［J］.电力建设，2015（8）：73-78.

Parameters Tuning for UPFC Auxiliary Damping Controller

SONG Pengcheng1，ZHEN Hongning2，WANG Zhenquan2，XU Zheng1，DONG Huanfeng1
（1.College of Electrical Engineering，Zhengjiang University，Hangzhou 310027，China；2.Jiangsu Electric Power Design Institute，Nanjing 211102，China）

In this paper，a new method of UPFC auxiliary damping controller parameters tuning based on test signal method is proposed.First，the small signal stability of power system is analyzed using the test signal method.Then the testing signal is scanned at the line active power setting point of UPFC while the active power flow in the parallel AC tie line is oscillated.The open-loop transfer function between the line active power setting point of UPFC and the active power flow in the parallel AC tie line is identified by Fourier resolution and curve fitting.Finally，the parameters of UPFC auxiliary damping controller are tuned based on the root locus rules of the classical control theory.The proposed parameter tuning method is validated by the simulation results of a simple case and a real power grid.

unified power flow controller（UPFC）；UPFC auxiliary damping controller；test signal method；parameter tuning method

TM761

A

1009-0665（2015）06-0010-04

2015-08-11；

2015-09-17

宋鹏程（1990），男，山东淄博人，博士研究生，从事大规模交直流电力系统分析、直流输电与柔性交流输电相关研究工作；

甄宏宁（1985），男，江苏南京人，工程师，从事电力系统规划相关研究工作；

王震泉（1980），男，江苏泰州人，工程师，从事电力系统规划相关研究工作；

徐政（1962），男，浙江海宁人，博士生导师，从事大规模直流电力系统分析、直流输电与柔性交流输电、电力谐波与电能质量、风力发电技术与风电场并网技术相关研究工作；

董桓锋（1990），男，浙江绍兴人，博士研究生，从事大规模交直流电力系统分析相关研究工作。