基于关联度分析的电网可靠性指标评价

吴　骏，李　珉，惠　峻

基于关联度分析的电网可靠性指标评价

吴骏，李珉，惠峻

（无锡供电公司，江苏无锡214061）

目前，基于可靠性指标评价现状电网的分析中，大多是根据工作人员积累的经验或按照复杂的公式计算指标权值对电网的影响程度，未有一种快速的方法去评判现状电网可靠性指标的影响程度。为此文中提出了一种关联度分析法，该方法用于现状电网可靠性指标评价，通过建立关联度分析函数快速计算各可靠性指标关联度，并且可以纵向上评判现阶段电网各可靠性指标的影响程度，进而找到现状电网可靠性的薄弱环节。最后结合算例结果验证该分析方法的合理性，为电网可靠性的建设方向提供较好的理论依据。

评价方法；可靠性指标；关联度分析；偏离度；改造方向

城市配电网建设发展是一项复杂艰巨的系统工程，具有规模大、不确定因素多、涉及领域广的特点［1］。对电网可靠性发展方向的把握，是通过对现状电网可靠性分析从而进行规划建设改造方案的确定和实施而实现的。而现状电网可靠性分析，则需要建立在电网现阶段真实详尽的评价分析的基础上，因此有必要建立科学快速有效的评价分析方法。

多目标决策是指在考虑多个目标的情况下，选择最优备选方案或进行方案排序的决策问题，在管理学、经济学、运筹学以及系统工程等学科研究中占有十分重要的地位，具有广泛的理论价值和应用前景。针对电网可靠性多指标评价的权值大小的确定，往往比较困难。目前已产生许多方法，例如特征向量法［2］、Delphi［3］、层次分析法［4，5］、专家咨询打分法［6］、优序图法［7］、模糊层次分析法［8］等主观权重法，及熵权法［9］、主成分分析法［10］、改进熵权法［11］、离差最大化客观赋权法［12］等客观权值法。主观权值法往往简单可行、操作方便，但易受到决策者知识、能力、经验等限制，随意性很大，不同的决策者废除的结果千差万别，直接影响到决策者的偏好程度；而客观权值法计算又往往过于复杂，不便于工程人员的运用。

1　关联度分析法

在实际的现状电网可靠性分析过程中，是不可能建立具体的电网决策变量函数，在此采用关联度分析的方法进行分析。首先需要考虑的问题是，众多的对电网可靠性决策变量产生影响的因素中，影响程度可能存在差别，或者说找出主要的影响因素是非常关键的。下面选取可靠性指标——系统平均停电时间（SAIDI）为例，结合关联度分析法做一个具体的评价分析。

1.1指标归一化方法

对具体问题进行统计分析离不开统计指标，统计指标是对分析对象的数量特征进行描述和分析的基本工具［13］。然而各指标由于性质不同、计量单位不同，往往缺乏综合性。为避免这一点，解决各指标数值可综合性问题，需对各指标数值进行归一化处理。利用指标极值（极大值或极小值）计算指标的归一化值xi*，即：

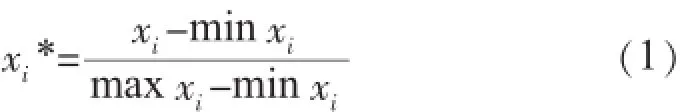
对可靠性指标，SAIDI根据连续两年及最优值可知，最大值为631.1 min，最小值为一流值11.5 min，现状值为622.7 min，所以得到归一化结果为1，0，0.986 4。

1.2关联度分析法

电力系统可以看成是一个运动系统，一般运动系统模型可以表达为：

将式（2）进行泰勒展开，忽略目标函数二次及以上的项：

因为在原始运行点上，各变量不发生变化，所以F［X0］=0，再令A=dF（X0）/dXX0，就可将上式整理得到：

式（4）中：A为关联向量，也是决策变量针对电网可靠性的关联度向量。当A中的某个元素较小时，可以认为对应的决策变量对经济或者可靠性的影响不大，可eF以从决策变量中剔除；ei为各指标的关联度，用* i表示。F（X）为电网的某特性，例如供电可靠性等。

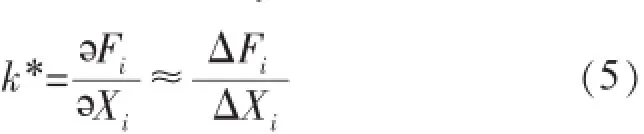
根据上文归一化数据，系统平均停电时间指标连续两年归一化结果为1和0.986 4，由式（5）得到，ΔF的值不影响k*的变化，定义为1，所以可靠性指标系统平均停电时间的关联度为73.762。

1.3关联度分析应用修正

结合工程建设的可实行性和可完成的实际情况，本文将电网可靠性指标的关联度发展趋势分为前期、中期和后期。前期是指标改善初期，基本处于很低的水平，此时关联度会很高；中期是指标改善快速时期，基本处于中等水平，关联度较大；后期是指标改善末期，这个时期已经基本达到一流水平，可提升量很低或是很难。具体变化趋势如图1所示。

这样就能近似地将一个非线性函数转换成一个线性函数［14］，从而简化了网络的模型，进行量化分析，其中ΔX的值取得越小，从非线性函数转换成的线性函数就越相似，分析的结果就越准确。根据收集的样本数据，将相邻2个状态的决策变量和电网特性指标相减，同时采取线性回归可以近似得到：

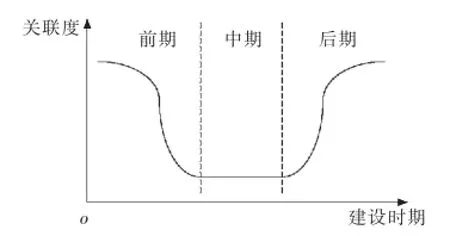
图1　指标关联度变化趋势

当某个可靠性指标发展到后期，即已经达到很高的水平，可提升量很低，在这个时期就会出现关联度分析的局限。因为此时的关联度理论上应该是很小的，但是通过式（5）可知，提升量低，即在ΔFi不变的情况下，ΔXi很小，会导致关联度很大，甚至会超过建设初期关联度。针对关联度分析存在的局限性，本文针对关联度分析局限的修正方法是引入了偏离度的概念。即：

式（6）中：对于系统平均停电时间，其中x是指标的实际值，为622.7 min；xN是指标基值，指标基值是在指标达到一流水平区间时选取的值，为11.5 min；D为偏离度，表示指标与一流水平的指标基值的偏离程度，由上述数据及式（6），计算得53.51。

从可靠性指标改善优先程度来说，在指标发展到后期，指标的偏离度越小，改善的优先程度越小，即关联度越低。但因为关联度分析的局限性，此时就必须要利用偏离度在关联度的基础上对指标再进行优先级优化，通过偏离度的引入可以消除关联度分析的局限性。

2　算例分析

选取某个城市的现状电网可靠性指标研究以验证该评价方法的实用性。该城市选取的指标均与可靠性相关，分别为系统平均停电时间（SAIDI）、系统平均停电次数（SAIFI）、输网平均停电时间（SAIDI-T）、输网平均停电次数（SAIFI-T）、城市用户供电可靠率、农网用户供电可靠率和10（20）kV电网N-1通过率。选取了A，B，C三组样本数据，其中C组数据是各指标经过改善提升的最优值，即指标基值xN，结合式（6）算出可靠性指标偏离度，并取均值表示A组和B组数据偏离度，具体指标基础数据及偏离度如表1所示。

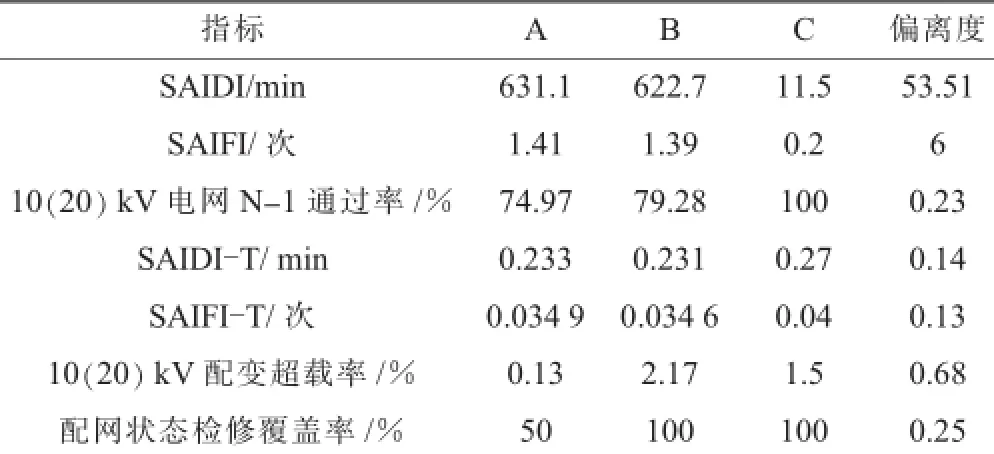
表1　评价对象指标基础数据与指标偏离度

由表1可知，该城市的SAIDI和SAIFI偏离度很大，说明这些可靠性指标距离一流水平还存在很大的差距，需要最优先改善。相比较而言，其他5组指标的偏离度很小，说明此类可靠性指标已经发展到很高的水平，可提升量较小，尤其是SAIDI-T和SAIFI-T。根据式（1）进行数据归一化处理，具体结果如表2所示。

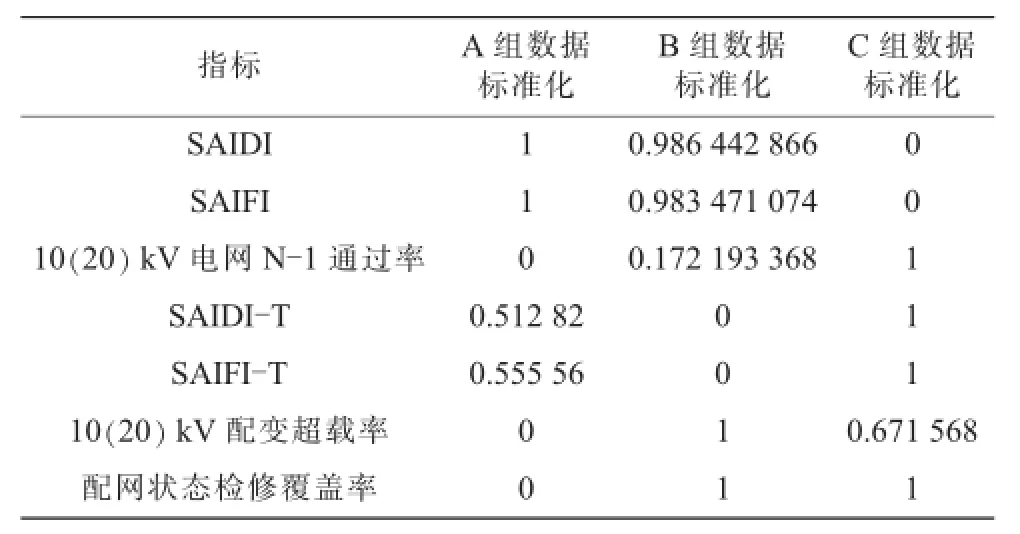
表2　数据标准化处理

再根据式（5）计算出各可靠性指标的关联度，具体结果如表3所示。

从表1和表3可知，SAIDI，SAIFI和10（20）kV电网N-1通过率的关联度很大，而10（20）kV配变超载率和配网检修覆盖率的关联度很小，说明该市现状电网指标改善应优先改善关联度大的指标。关联度的大小可以很清晰的反映出现状电网安全质量类特性的各指标的关联程度，该结果也符合各指标对电网的实际影响程度，同时也符合现状电网实际指标改善的优先度。但是SAIDI-T和SAIFI-T的关联度很大，而SAIDI-T和SAIFI-T的偏离度非常小，说明该指标已经发展到后期，可提升量很小，已经不能认为该指标对电网的影响程度很大，所以在电网实际指标改善措施中，该指标不作为指标改善的重点。

通过分析各可靠性指标的关联度，可以纵向上比较各指标对现状电网的影响程度，同时也可以找出该城市现状电网安全质量特性的薄弱环节，利用关联度的大小，判断各可靠性指标改善的优先级，同时结合偏离度分析，可以克服关联度分析的局限，对关联度分析结果进一步优化，从而对现状电网的可靠性优化建设指明方向。

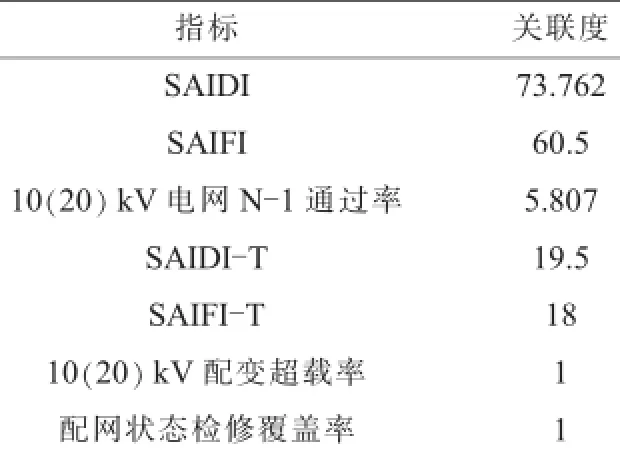
表3　各指标关联度

3　结束语

本文提出了适合电网可靠性评价指标纵向对比的客观研究方法——关联度分析法。该研究方法不仅不同于以往的主观权重法，不基于决策者的偏好程度，也不同于客观权重法，不需要建立复杂的熵权的计算，能够快速地、合理地计算出各可靠性指标的关联度，可以纵向上比较各指标的关联度大小，从而判断各指标对电网的影响程度，同时引入偏离度的概念，能有效地克服关联度分析的局限，从一定程度上完善关联度分析法，而且还能够客观有效地找出电网可靠性的薄弱环节，能够明确电网可靠性建设的改造方向，具有实际的指导意义。

［1］韩震焘，黄志伟，葛少云，等.城市配电网综合评价体系［J］.电网技术，2012，36（8）：95-99.

［2］SAATY T L.A Scaling Method for Priorities in Hierarchical Str u ctures［J］.Journal of Mathematical Psychology，1977，15：234-281.

［3］HWANG C L，LIN M J.Group Decision Making Under Multiple Criteria：Methods and Applications［M］.New York：Springer-Verlag，1987：318-335.

［4］张蔓，林涛，曹健，等.理想区间法在电能质量综合评估中的应用［J］.电网技术，2009，33（3）：33-38.

［5］沈阳武，彭晓涛，施通勤，等.基于最优组合权重的电能质量灰色综合评价方法［J］.电力系统自动化，2012，36（10）：67-73.

［6］王宇亮，刘智慧.基于模糊数学理论的桥型方案比选模型［J］.工程设计与建设，2005，37（1）：14-17.

［7］金新政，厉岩.优序图法和层次分析法在权值时的比较研究及应用［J］.中国卫生统计，2001，18（2）：119-120.

［8］姜艳萍，樊治平.一种三角模糊数互补判断矩阵的排序方法［J］.系统工程与电子技术，2002，24（7）：34-36.

［9］贾正源，赵亮.基于熵权未确知测度模型的电能质量综合评价［J］.电力系统保护与控制，2010，38（15）：33-37.

［10］周慧成，张改红，王国利.基于熵权的水库防洪调度多目标决策方法及应用［J］.水利学报，2007，38（1）：100-106.

［11］李英海，周建中.基于改进熵权和Vague集的多目标防洪调度决策方法［J］.水电能源科学，2010，28（6）：32-35.

［12］董一哲，党耀国.基于离差最大化的灰色聚类方法［J］.系统工程理论与实践，2009，29（9）：11-16.

［13］马力平.统计数据标准化［J］.北京统计，2000（3）：34-35.

［14］季晓明，成乐祥.基于突变理论的配电网规划方案综合评价［J］.江苏电机工程，2014，33（5）：31-34.

Network Reliability Evaluation Based on Association Analysis

WU Jun，LI Min，HUI Jun
（Wuxi Power Supply Company，Wuxi 214061，China）

The current multiple indicator evaluation methods for the current situation of power grid are mostly based on the accumulated experience of staff or by defining indicators to measure the impacts on power grid，and there isn't a quick way to judge the influence levels of indicators of the current situation of power grid，so this paper proposes a method called correlation analysis to research the multidimensional evaluation of the current situation.The correlation analysis is to determine the correlative degree size of each index，and longitudinal comparison is to analyze the current influence level of each indicator for revealing the weakness of power grid.Finally，the simulation results verify the proposed method，and it provides the theoretical basis of system reliability for power grid construction.

evaluation method；reliability index；correlation analysis；degree of deviation；reconstruction direction

TM727

B

1009-0665（2015）06-0082-03

2015-08-08；

2015-09-19

吴骏（1966），男，江苏苏州人，高级工程师，从事电网规划建设工作；

李珉（1973），男，浙江东阳人，研究员级高级工程师，从事电网规划建设工作；

惠峻（1977），男，江苏无锡人，工程师，从事电网规划建设工作。