基于粒子群算法的MMC-UPFC参数优化

林子杰，刘建坤，陈　静，张宁宇，孙国强，卫志农

仿真分析

基于粒子群算法的MMC-UPFC参数优化

林子杰1，刘建坤2，陈静2，张宁宇2，孙国强1，卫志农1

（1.河海大学能源与电气学院，江苏南京211100；2.江苏省电力公司电力科学研究院，江苏南京211103）

作为柔性交流输电（FACTS）中功能最强的设备，统一潮流控制器（UPFC）可以实现对线路传输的有功功率和无功功率独立控制、优化系统潮流分布、提高稳定性。文中在分析现有MMC-UPFC控制策略基础上，以其对指令的跟踪能力作为优化目标，提出一种基于粒子群算法控制参数优化方法。利用Matlab和PSCAD/EMTDC建立某实际电网中MMC-UPFC模型并实现了该优化算法。优化前后MMC-UPFC的仿真结果证明，粒子群算法能有效优化MMC-UPFC的控制参数。关键词：模块化多电平换流器（MMC）；UPFC；粒子群算法；参数优化

统一潮流控制器（UPFC）是目前为止功能最强大的柔性交流输电（FACTS）［1］装置，其自问世以来就受到了广泛的关注。近年来，对于UPFC的研究主要集中在其数学模型、控制策略以及对电网的影响［2，3］等方面。数学模型主要有功功率注入模型、独立支路模型等；控制策略主要有基于幅值和相角控制的比例—积分（PI）控制［4］，d-q解耦控制法［5］以及节点电流注入法［6］等。

目前，基于比例—积分（PI）控制器的dq解耦双环控制策略［7］在诸多已经投运的UPFC示范工程中得到广泛运用，通过优化设定PI控制器控制参数，可以改善UPFC装置的稳态、动态性能，但是该策略的控制参数主要依靠人为经验来设定，且相关的调试工作量大。基于此，本文利用粒子群算法精度高、收敛快且可以并行运算的优点，提出了基于粒子群算法的MMC-UPFC的控制参数优化方法。通过Matlab/Simulink与PSCAD/EMTDC的联合仿真，证明了所提方法能有效提高MMC-UPFC的性能。

1　模块化多电平换流器数学模型

模块化多电平换流器（MMC）通过将多个标准子模块（Submodule）的输出电压的叠加产生多电平交流电压，具有电压等级高，传输容量大的特点。相比于传统两电平、三电平换流器更能够满足UPFC的需求。

MMC的拓扑结构以及子模块结构的示意图如图1所示。子模块由一个IGBT半桥和直流储能电容构成。通过控制开关VT1，VT2的通断，可使端口电压在0和子模块电压uSM之间切换。

换流器由3个相单元组成，每个相单元由上、下2个桥臂构成。通过控制每个桥臂中子模块的切、投可以控制输出的瞬时电压，各桥臂可以用一个受控电压源等效。为了保持直流电压稳定，每个相单元中，2个桥臂投入的子模块数之和恒定。

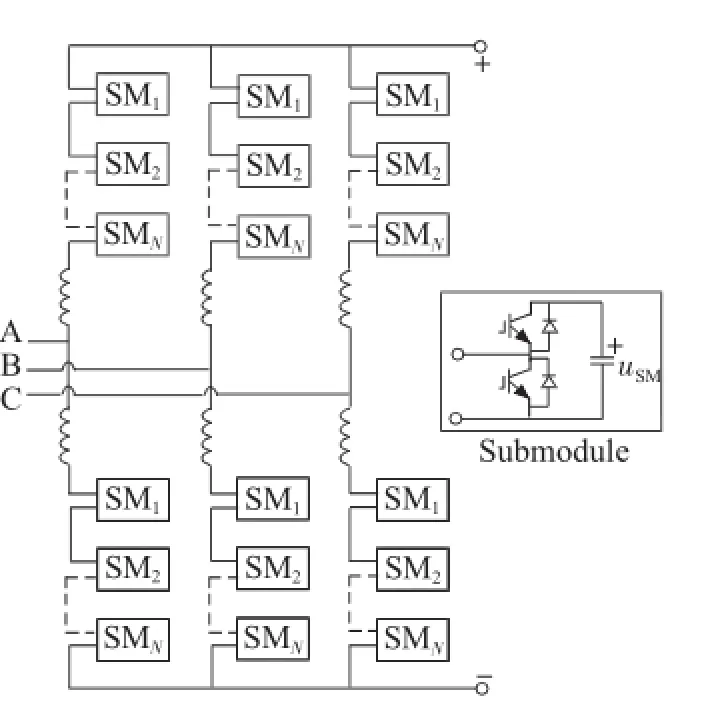
图1　MMC拓扑结构示意图

MMC的调制技术有多种，应用最广泛的是最近电平逼近（NLM）。NLM的本质在于使输出的方波尽量逼近于调制波，一般通过下面的表达式求到每个桥臂需要投入的子模块数nup，ndowm。

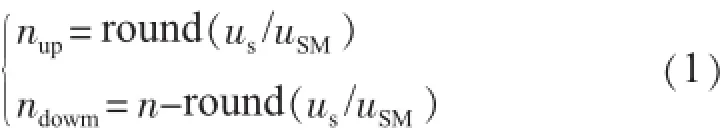
式（1）中：n为每相投入的总模块数；us为调制波瞬时值。

2　MMC-UPFC的数学模型

MMC-UPFC基本结构如图2所示。主要由2台模块化多电平换流器以及串、并联变压器组成。并联换流器（MMC1）通过并联变压器Tp并联接入系统，通过直流侧向串联换流器（MMC2）提供有功功率支持，同时可以往系统注入或吸收无功功率以维持送端电网电压。MMC2通过串联变压器Ts向输电线路中串入一个幅值、相角可调的同步电压，以控制输电线路流过的潮流。图2中，V.1，V.2分别为输电线路首、末端的电压向量；Pp，Qp分别为MMC-UPFC并联侧向系统注入的有功功率和无功功率；PL，QL为线路输送的有功和无功率；V.p，V.s为MMC1，MMC2交流侧的电压基波向量；I.s为输电线路电流向量；I.p为MMC1注入系统电流向量；Udc为直流母线电压；LL为输电线路等效电感。

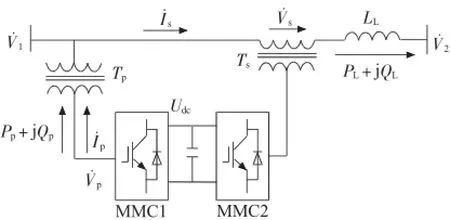
图2　MMC-UPFC基本结构图

忽略串、并联变压器电阻以及换流器的损耗，将MMC1，MMC2用2个电压源等效，TP，Ts分别用各自的漏电感LP，Ls等效，可以得到如图3所示的简化等效电路。

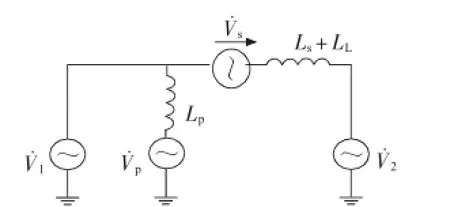
图3　MMC-UPFC简化等效电路图

通过park变换可以得到并联侧在d-q坐标下的数学模型。

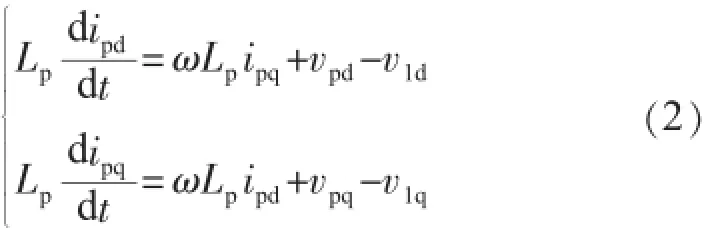
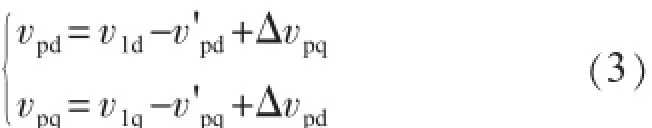
式（3）中

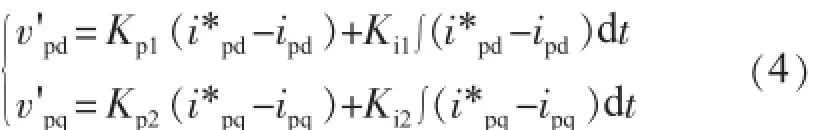
为了实现dq轴电流的解耦控制，引入电流交叉耦合项Δvpd，Δvpq解耦非线性方程以及使用送端电网扰动电压v1d，v1q进行前馈补偿，使得控制系统具有快速、稳定的动态特性。取送端电网电压为参考向量，在三相对称运行时，送端电网电压矢量为d轴的方向，即v1d= V1，v1q=0，则：

考虑式（3）中v'pd，v'pq和ipq，ipd之间的一阶微分关系，引入比例积分环节的对其进行控制，可以得到控制方程：

由式（5）可见，有功功率与无功功率分别受ipd和ipq的控制。利用PI控制器对ipd和ipq进行控制，可以对MMC1与输电系统之间交换的有功功率和无功功率独立控制。

根据式（3—5）设计的并联侧控制器如图4所示。

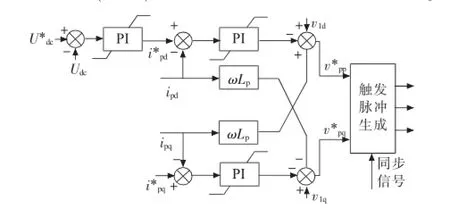
图4　并联侧换流器解耦控制器

对图3所示等效电路进行进一步简化，可以得到串联侧简化等效电路，如图5所示。

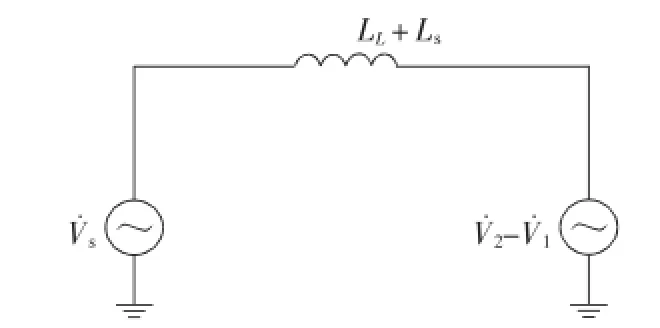
图5　串联侧简化等效电路

从图5可以得到串联侧在d-q坐标下的数学模型。令Lk=LL+Ls，参考上述并联侧控制器的建模，可以得到串联侧控制器，如图6所示。

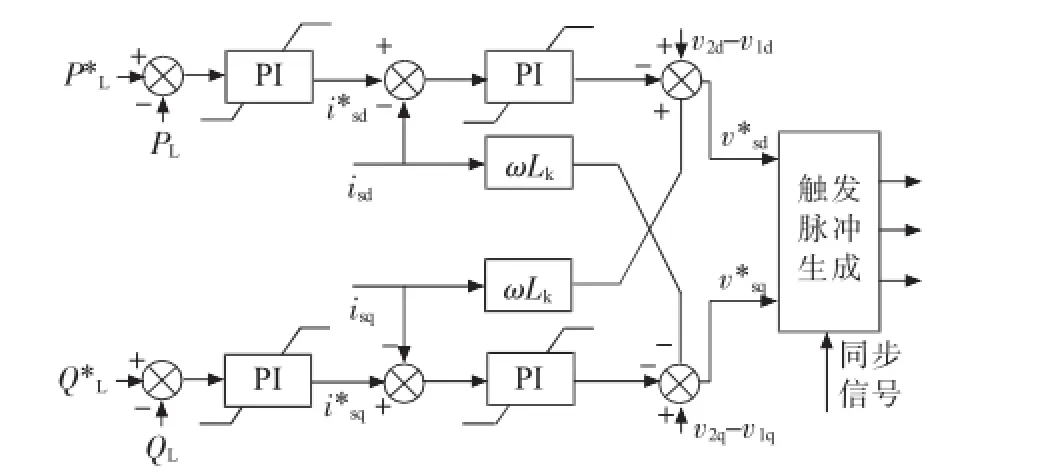
图6　串联侧换流器解耦控制器

3　控制参数优化

由上一节的建模可知，MMC-UPFC是一个强非线性的系统，很难通过解析的方式对控制参数进行优化。基于上述情况，利用粒子群算法易于实现、收敛速度快、搜索精确度高的优点对MMC-UPFC控制参数进行优化。粒子群算法以随机解作为起点，用一个目标函数来判断解的优劣，通过迭代寻优。算法流程如下：

（1）随机生成一定数量（一般取10～20）粒子的初始位置和初始速度。

（2）计算每个粒子的适应度，并把当前位置记录到个体最优位置中，把所有粒子里面的最优粒子记录到群体最优位置中。

（3）根据粒子当前位置和速度更新位置，各个粒子的个体最优位置和群体最优位置更新粒子速度。

（4）计算每个粒子的适应度，并与当前的个体最优和群体最优值对比，更新个体和群体最优位置。

（5）判断当前迭代结果是否满足精度要求或者迭代次数是否到达最大迭代次数，若是则停止运算并输出结果，否则返回步骤（3）。

基于粒子群算法的MMC-UPFC参数优化具体流程如图7所示。

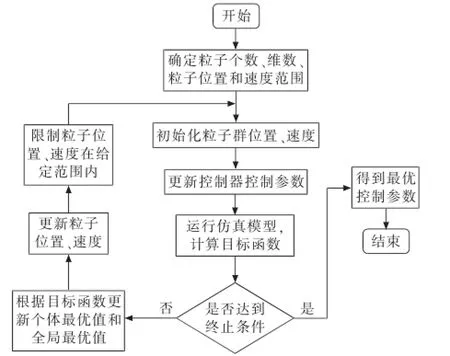
图7　控制参数优化流程图

从图4、图6中可知，本文使用的控制模型总共使用了7个PI控制器，取各个PI控制器的比例系数和积分系数作为优化对象。即取：

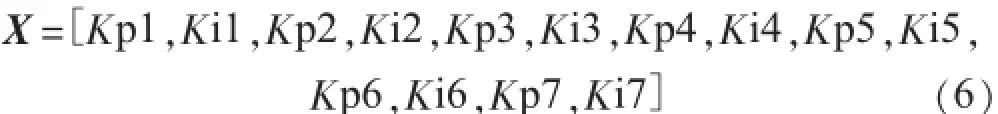
本文以时间乘绝对误差积分（ITAE）作为粒子群算法寻优的目标函数，式（6）为其基本表达式。其中t为扰动发生的时间；为误差的绝对值；T为一个时间定值，一般取一个足够大的时间以保证系统能进入稳定。JITEA作为优化目标函数具有良好的参数选择性，可以使系统动态响应过程快速、平稳、超调量小。

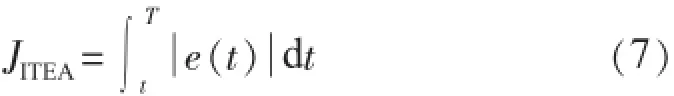
本文主要考虑UPFC在暂态过程中直流侧电压、线路传输的有功功率和无功功率的动态特性，故设置目标函数为：

式（8）中：ωDC，ωP，ωQ分别为直流侧电压、线路传输的有功功率和无功功率的ITAE指标在总指标中所占的权重，可根据不同的工程需求分配，本文中3个权重都取1.0，误差的计算均使用标幺值。

4　仿真验证

为了验证本文描述的控制系统以及提出的参数优化方法的有效性，在PSCAD/EMTDC中建立了江苏省某市实际电网中的MMC-UPFC模型，并利用MATLAB调用PSCAD模型进行参数优化。UPFC参数如表1所示。

所有变量采用标幺值，基准值SB=100 MV·A，UB= 220 kV初始设定有功功率为-0.4 p.u.，无功功率为0.1 p.u.。t=0.6 s时刻，将有功功率参考值设为0.0 p.u.，无功功率参考值设为0.5 p.u.。由于系统一般在0.1s内能进入稳定状态，取0.6 s到0.7 s之间的过程计算ITAE指标。如表2所示。

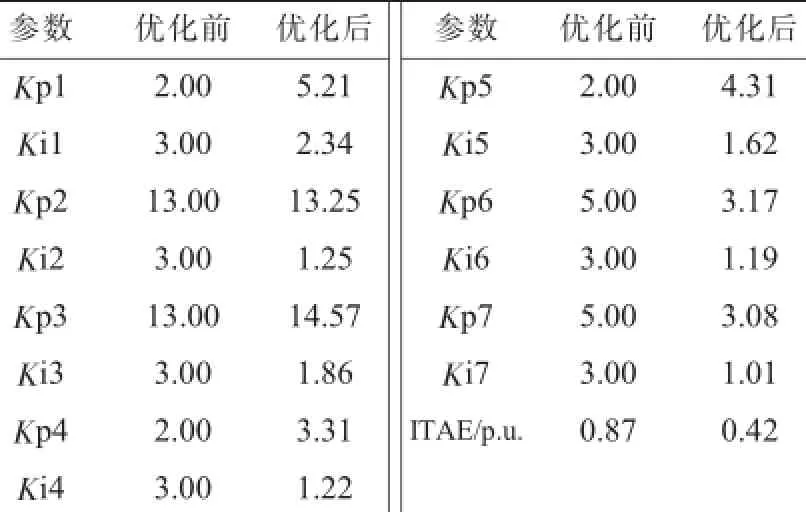
表2　参数优化结果

优化前后线路的有功功率、无功功率以及UPFC直流侧电压的情况如图8—10所示。

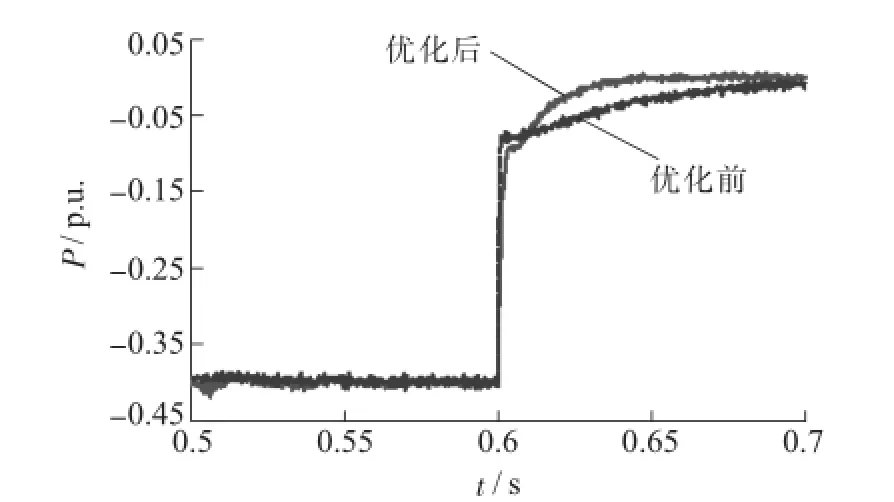
图8　线路传输的有功功率

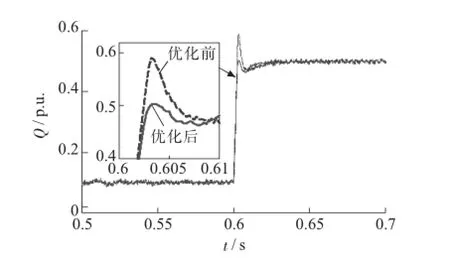
图9　线路传输的无功功率

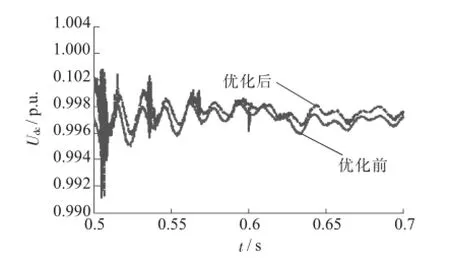
图10　UPFC直流侧电压

从仿真结果可以看出，利用粒子群算法对MMC-UPFC控制参数进行优化后，在系统有功及无功指令发生阶跃变化时，ITAE指标从0.87 p.u.减小至0.42 p.u.，线路传输有功功率对指令的跟踪能力得到较大提高，无功功率超调量从0.09 p.u.下降到0.01 p.u.，由于有功功率变化时，MMC-UPFC直流部分传输功率变化不大，直流电压的波动较小，参数优化的效果相对较小。总体来说，系统的动态性能得到了很大改善。

5　结束语

本文利用粒子群算法，用有功功率及无功功率参考指令变化时暂态过程的加权ITAE指标作为目标函数，对MMC-UPFC模型的控制参数进行优化。仿真结果表明，MMC-UPFC系统的控制参数经过优化后，动态性能得到较大的改善，ITAE指标能较好地反映MMC-UPFC的动态性能；本文提出的优化方法有效，且具有一定的推广使用价值。

［1］GYUGYI L，SCHAUDER C D，WILLIAMS S L，et al.The Unified Power Flow Controller：a New Approach to Power Transmission Control［J］.in Power Delivery，IEEE Transactions on，vol.10，no.2，1995：1085-1097.

［2］邱婕，刘峰，马波.计及统一潮流控制器的无功优化研究［J］.江苏电机工程，2007，26（3）：21-23.

［3］吴红斌，杨仪松，丁明.含统一潮流控制器的电力系统概率暂态稳定评估［J］.江苏电机工程，2006，25（6）：6-8.

［4］ZHENG Y H，YI X N，SHEN C M，et al.Application of Unified Power Flow Controller in Interconnected Power Systems-modeling，Interface，Control Strategy，and case study［J］.in Power Systems，IEEE Transactions on，vol.15，no.2，2000：817-824.

［5］杨勇，阮毅，吴国祥，等.基于DPWM1的无差拍解耦控制的三相并网逆变器［J］.电工技术学报，2010（10）：101-107.

［6］陈业飞.基于节点电流注入法的UPFC控制策略研究［D］.天津：天津大学，2013.

［7］刘黎明，康勇，陈坚，等.UPFC的交叉耦合控制及潮流调节能力分析［J］.中国电机工程学报，2007（10）：42-48.

A PSO Algorithm based Approach for Optimizing MMC-UPFC Control System Parameters

LIN Zijie1，LIU Jiankun2，CHEN Jing2，ZHANG Yuning2，SUN Guoqiang1，WEI Zhinong1
（1.College of Energy and Electrical Engineering，Hohai University，Nanjing 211100，China；2.Jiangsu Electric Power Company Electric Power Research Institute，Nanjing 211103，China）

As one of the most powerful flexible AC transmission system（FACTS）devices，the unified power flow controller （UPFC）can control the active and reactive power on the transmission line independently，optimize the system power flow distribution as well as improve the system stability.In this paper，the control strategy of the existing MMC-UPFC is analyzed. Based on the analysis，a particle swarm optimization based approach to optimize the control parameters is presented.The proposed approach takes the tracking ability to the reference value as the optimization objective.The MMC-UPFC model of a real system and the optimization algorithm are realized in Matlab and PSCAD/EMTDC.Simulation results show that the proposed approach is effective.

modular multilevel converter（MMC）；unified power flow controller（UPFC）；PSO；parameters optimization

TM762

A

1009-0665（2015）06-0023-04

2015-08-13；

2015-09-25

林子杰（1992），男，广东广州人，硕士研究生，研究方向为电力系统运行分析与控制；

刘建坤（1980），男，山东潍坊人，高级工程师，从事电力系统计算和分析工作；

陈静（1988），女，江苏南通人，工程师，从事电力系统分析工作；

张宁宇（1985），男，山西五台人，工程师，从事电力系统规划与优化计算工作；

孙国强（1978），男，江苏江阴人，副教授，研究方向为电力系统运行分析与控制；

卫志农（1962），男，江苏江阴人，博士研究生导师，研究方向为电力系统运行分析与控制、输配电系统自动化等。