量子计算与量子信息简介

王帮海，龚洪波

（广东工业大学计算机学院，广州　510006）

量子计算与量子信息简介

王帮海，龚洪波

（广东工业大学计算机学院，广州510006）

0　引言

电子计算机的产生与发展不仅深刻地改变了人们的生活，也深刻的影响着人们的思想。特别是计算机网络的应用与发展，计算机与人类生活的密切程度，已经远远超出了人们当初的想象。计算机的计算速度、存储容量都遵循着Moore定律：每三年翻一番［1］。按照这个速度，十多年以后计算机存储单元将是单个原子，届时就会出现集成电路中电流不稳定、热量在技术上难以散发以及受到量子效应干扰等现象［2］。同时，传统的计算机体系结构――冯诺依曼结构在人类探索世界奥妙的雄心壮志面前显得力不从心［3］。人们从冯诺依曼结构出发，不断地提出各种新型结构的计算机。

量子计算就是新型结构的计算模型之一 （值得一提的还有生物计算或分子计算）。量子计算与量子信息（这两方面一般合起来称作 “量子信息学”）是量子力学、计算机科学与信息理论等交叉融合产生的新兴学科［4］。本文介绍量子计算的起源、基本概念、以及与经典相比量子基本特性、基本原理和它们的应用。本文力求避免数学符号、物理概念，希望具有一点线性代数知识的读者能对量子信息学有一个初步的了解。

1　量子信息学发展简史

众所周知，20世纪初就发现了量子力学，但是直到20世纪30年代才差不多被人们所普遍知晓。当物理学家在尝试着用计算机模拟量子力学时，产生了量子力学可能会使（量子）计算比经典计算更先进的念头。因为对n个量子比特来说，总共需要2n个复数才能完全描述它，而不是2n个。量子力学的这种指数级的状态空间，使人们自然的想，它有没有包含一个超乎我们想象的更大、更强的计算资源。1982年，理查德费曼觉得也许基于量子力学的计算机可以执行任务更高效，因为传统计算机似乎需要指数开销模拟量子力学，因而产生了量子计算可能比传统计算更有优势的想法。1985年，英国牛津大学教授D.Deutsch引进量子计算线路模型和量子通用逻辑门组，提出量子图灵机的概念，使量子计算开始具备数学的基本型式。

更早的，有关量子信息学的研究可以追溯到几十年前的可逆计算的研究和贝尔不等式的发现，但真正引起人们普遍关注并掀起研究热潮的是二十世纪九十年代中期。在这期间，Shor提出了量子并行计算的大数因数分解算法，Grover提出了快速的基于无先验结构信息的量子搜索算法。大数因数的快速分解宣示着目前广泛应用于密码通讯中的公钥体制RSA算法不再具有计算安全性；Grover快速量子搜索算法能够快速地找到DES加密算法算法密钥，意味着DES算法将不堪一击［5］。

2　量子比特与量子门

一般来说，经典电子计算机处理的只有“0”、“1”两个基本状态，往往用电压或者电流有无来表示，或者不同的数值，例如+5伏电压表示1，-3伏电压表示0。

量子计算处理的基本元素是量子比特。量子力学系统由希尔伯特（Hilbert）空间中的向量表示，表示量子态的向量称状态向量。一般情况下，具有d个可完美区分的量子态的量子系统能够用复线性空间Cd中的一个单位向量描述。这个最简单的情况是d=2。这样的系统，我们称作一个量子比特。因为｝是一个二维复向量空间的正交基，所以任意向量］可以表示为，其中a和b都是复数。］被称为一个量子比特，常被称作叠加态（superposition），］称为计算基态，也不严格的称为量子中的“0”、“1”。与经典比特不同，我们不能通过测量量子状态来确定它是哪个具体的量子状态，也就是得到a和b的值。事实上，量子力学告诉我们，只能得到量子状态的有限信息。也就是说，一个量子态往往不是确定的，只是这两种基态的线性组合，也就是说，一个量子态中含有两个变量参数，这样n个量子比特里至少含有2的n次方信息。在测量量子比特时，我们得到态的概率为|a|2，态的概率为|b|2。由于概率和总是等于1，当然就有|a|2+|b|2= 1。这就是量子态的归一化，从几何意义上看，就是要求量子比特的状态归一化到长度1。所以，一般而言，量子比特的状态是二维复向量空间中的单位向量。例如，一个比特量子态。如果使用基｝进行测量，50%的可能得到，50%的可能得到］，如果使用基｝进行测量，则得到概率）是100%，得到的概率是0。这种奇妙的结果是量子力学所独有的，进一步的了解可参照参考文献［1-5］等。

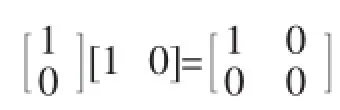
至于为什么量子比特用向量或者矩阵表示 （等同的，也可用波函数表示，这里不详述），这缘于量子力学的基本假设。自从牛顿创导模型与数学相结合的科学研究方法以后，几乎物理学的每一步发展也离不开模型和数学。把实际的物理问题简化并使之能直接应用数学就是物理模型，采用的办法往往就是作“假设”。对于量子领域的问题，人们很少有直接的感觉经验，“假设”就显得尤其重要。量子力学的假设是先驱们经过了大量猜测和摸索，甚至是长期的尝试与失败而得到的。它把物理世界和数学描述联系了起来，它界定了物理理论或者物理概念的适用范围。任何一个物理理论都有其适用范围。对于我们目的而言，坚持这些假设就足够了［6］。

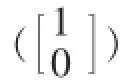
3　量子基本特性及其应用

量子力学为信息学带来了这些令人耳目一新的现象的根源在于量子的两个基本特性：量子线性叠加和量子纠缠。

（1）量子线性叠加

量子线性叠加原理是指任一量子系统都可以表示为描述量子系统不同状态（量子态）的线性组合，表现为如果输入是多个可能输入状态的线性组合时，输出态也将是所有输入态对应输出态的线性组合，这是量子物理最基本、最显著的原理，也是量子并行计算的核心［3，5］。

为了原理性的描述量子并行计算的机制，人们常常以Deutsch问题为例说明。设一个函数f，若f（0）=f （1），则称f为常数函数，否则称为平衡函数。现假设一个量子装置可以计算f（x），现在的任务是判断f（x）是常数函数还是平衡函数。很明显，如果是经典输入，必须运行这个装置两次才能得到结果，而如果是量子输入则只需运行量子装置一次。具体运算机制，读者可参考文献［4］等。

（2）量子纠缠及其应用

此时此地发生的某件事情能够在万里之外的同一时刻引起某种反应，这可能吗？我们对某一个观测量的测量，在同一时刻，千里之外，或者世界的另一头，甚至宇宙的边缘（假如存在），一个类似的行为也会发生，这可能吗？令人惊奇的是，与我们的直觉相反，这种现象确实存在，这就是“量子纠缠”（quantum entanglement）。纠缠中的两个粒子互相关联在一起，无论它们之间的距离多么遥远［7］。自从1935年薛定谔创造“纠缠”［8］这个词来描述这种关联以来，人们对“纠缠”的理解与探索就没有停止过。量子纠缠是量子力学独特的重要的资源，处于量子信息学的中心位置，在量子计算与量子信息的应用上起关键作用，参考文献［9］把它比作经典世界中青铜器时代中的铁的地位。

很明显，量子纠缠涉及到两个或者两个以上粒子的复合系统。数学上用张量积“⊗”描述系统间的关联。例如，密度矩阵表示系统以pi的概率处于状态ρi⊗σi，而ρi描述的是第一个系统的状态，σi描述的是第二个系统的状态。张量积的运算规则，感兴趣的读者可参考文献［9］等。

（1）量子超密编码

超密编码（superdense coding）是利用两个量子态纠缠特性的量子力学的一个简单的应用，最初由Bennett和Wiesner提出［9，10］。具体来说，就是收送双方共同拥有量子纠缠态，通过量子信道传送量子态，实现发送者发送一个量子比特，接收者得到两个经典比特的信息过程。习惯性的，把涉及的两方分别称为Alice和Bob。应用的情形是他们彼此相距很远，Alice要给Bob传送两个经典比特信息，但是只允许发送一个单量子比特给Bob。这种超出经典的直觉想象的任务，利用量子超密编码就可以完成。

（2）量子隐形传态

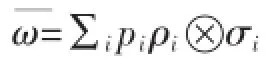
4　量子基本原理及其应用

量子世界有着与经典世界不同的特性，这些特性往往使“经典的”我们很难理解。下面不作证明的，介绍这些量子基本原理。事实上，数学上证明并不难，感兴趣的读者，可参考［1-5］、［9］、［13］等。

定理1：不能同时精确知道一个粒子的位置与动量。这就是大家所熟知的海森堡测不准原理。现在我们一般把它称为海森堡测不确定性原理。

定理2：无法可靠区分两个非正交量子态。

定理3：未知的量子态不能完全被克隆。这与经典非常不同，经典计算机之所以有今天这么广泛的应用或许与能“随意”拷贝密不可分。

上面这三个基本原理在本质上是统一的［13］。这些也是量子保密通信具有无条件安全的基础。

独立于量子计算，现在公认的最早的量子密码术出现于上个世纪70年代。当时还是研究生的Stephen Wiesner提出了量子货币的概念，希望用量子力学的方法增强钞票的防伪能力。当时的想法远远超前，他的论文处处碰壁，直到1983年才最终正式发表。但正是它启发了随后的BB84量子密钥分配协议的提出，从而引发了一场密码学技术革命［6］。

量子密码术一般包括两种不同的形式：量子密钥分配（QKD）以及从加密算法本身出发实现量子加密。量子密钥分配是指通信双方无须事先共享秘密的情况下产生一个随机安全密钥的过程。这样通信双方无须事先交换密钥就能进行秘密通信，因此量子密钥分配是量子密码的基础。海森堡不确定原理则是量子密钥分配的理论保证。因为海森堡不确定性原理告诉我们对一个量子态的测量必将引起原来量子态的扰动，对量子系统的任何测量都无法获取测量前的量子信息。这就意味着，一旦窃听者窃听量子信道的量子态时，必将对量子态造成干扰，对Alice和Bob双方的测量结果发生变化，从而提醒非法用户的存在。

5　发展与展望

量子信息学在不断的发展，其研究内容也在不断的扩充。目前，这一研究领域主要包含三个方向：（1）量子计算机和量子算法；（2）量子密码学；（3）相关的信息理论问题。方向（3）主要是将传统的信息熵、信道容量等信息学理论问题在量子力学层面推广到新内容以及带有量子力学独特特性的量子纠缠度的度量，等等。它是量子信息学发展比较迟的一个分支，有些问题甚至距离形成统一的定论都比较遥远，至今尚未完全成熟［4］。

目前，量子计算的实现采用的技术有核磁共振、光量子、量子几何相位、超导/介观电路等［4］。无论哪种方案，目前最大的问题是量子退相干。量子退相干是指量子系统不可避免地会与环境自发的耦合，导致其状态受到干扰而出现不可逆的错误，量子效应消失。目前量子系统能保持相干的时间非常短，还不足以保持到量子计算达到实用的程度。

令人鼓舞的是，量子保密通信，已经进入实用阶段，并且中国走在了世界的前列。2014年4月，中国开始铺设目前世界上最长的包括连接北京与上海的2000多公里的量子通信网络［14］。

由于大型量子计算机还未建立，因此量子信息对计算机科学的大部分贡献还处于理论阶段。但是一旦大型量子计算机建立成功，我们期望这些理论能应用在理论家难以解释的方面，就像我们今天在经典启发下成功发现了简单量子算法。历史告诉我们，很多这样的新工具最初是违反常识的，但是当我们掌握了它们之后，这些工具将会带领我们以全新的方式来认识世界［15］。

［1］佐川弘幸，吉田宣章著.突破经典信息科学的极限――量子信息论.宋鹤山，宋天译.大连理工大学出版社，2007，9.

［2］王帮海.基于纠缠破坏信道与纠缠目击者的可分标准研究.博士论文：中山大学计算机系，2011，6.

［3］戴葵，宋辉，刘芸，谭明峰.量子信息技术引论.湖南：国防科技大学出版社，2001，3.

［4］何广平著.通俗量子信息学.北京：科学出版社，2012.

［5］赵生妹，郑宝玉.量子信息处理技术.北京：北京邮电大学出版社，2010-1.

［6］金尚年.量子力学的物理基础和哲学背景.上海：复旦大学出版社，2007-7.

［7］A.D.Aczel.Entanglement：The greatest mystery in physics.John Wileyand Sons Ltd.2002.庄星来译.纠缠态：物理世界第一迷.上海：上海科技文献出版社，2008-7.

［8］E.SchrAodinger.Die gegenwartige Situation in der Quantenmechanik（TheCurrent Situation in Quantum Mechanics）.Naturwissenschaften，1935，23：807-812.

［9］M.A.Nielsen and I.L.Chuang.Quantum computation and quantum information.Beijing：Higher Education Press，2003.

［10］C.H.Bennett and S.J.Wiesner.Communication via one-and two particle operators on Einstein-Podolsky-Rosen states.Physical Review Letters，1992，69：2881.

［11］C.H.Bennett，G.Brassard，C.Crepeau，R.Jozsa，A.Peres and W.K.Wootters.Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels Physical Review Letters，1993，70：1895.

［12］D.Bouwmeester，J.W.Pan，K.Mattle，et al.Experimental quantum teleportation.Nature，1997，390：575-579.

［13］温巧燕，郭奋卓，朱甫臣.量子保密通信协议的设计与分析.北京：科学出版社，2009，6.

［14］Jane Qiu.Quantum communications leap out of the lab.Nature，2014，508：4 4.

［15］Aram W.Harrow.Why now is the right time to study quantum computing arXiv：1501.00011.

Quantum Computation and Quantum Information；the Brief History of Development；Basic Concept；Basic Characteristics；Basic Principles

The Introduction of Quantum Computation and Quantum Information

WANG Bang-hai，GONG Hong-bo
（School of Computer Science and Technology，Guangdong University of Technology，Guangzhou 510006）

国家自然科学基金资助项目（No.61272013）

1007-1423（2015）22-0018-05

10.3969/j.issn.1007-1423.2015.22.004

王帮海（1974-），男，副教授，博士，研究方向为兴趣为量子计算与量子信息

2015-07-30

2015-08-05

介绍量子计算与量子信息的产生背景、发展简史，量子比特与量子门的数学描述以及它们与物理概念之间的关系。介绍量子并行基础的线性叠加、量子力学独特资源的纠缠及其应用。介绍量子密码无条件安全的理论基础、发展历史，量子信息学研究、量子计算机实现的现状，并对未来作展望。

量子计算与量子信息；发展简史；基本概念；基本特性；基本原理

龚洪波（1989-），男，在读硕士研究生，研究方向为量子计算与量子信息

Introduces the background and the brief history of quantum computation and quantum information，describes the mathematical description of qubits and quantum gates and the relation between the mathematical description and their physical concepts.Introduces the linear superposition principle，which is the foundation of parallel computation，and quantum entanglement which is the unique property of quantum mechanics，and its application.Introduces the theory foundation of unconditional security of quantum cryptography and its history，introduces the current situation of the research on quantum information theory and the implement of quantum computer，and the future perspective of quantum computation and quantum information.