一维Theta神经元网络中的行波解对参数的依赖性

高菲菲

（内蒙古财经大学统计与数学学院，呼和浩特　010070）

一维Theta神经元网络中的行波解对参数的依赖性

高菲菲

（内蒙古财经大学统计与数学学院，呼和浩特010070）

0　引言

在文献［1］中，作者Remus Osan等人对一维Theta神经网络模型进行了研究，证明出了当突触传导系数gsyn充分大时，有两个波速c与之对应，使得模型中神经元的行波解确实存在。在文献［2］中，作者对同一神经网络模型进行了研究，证明了多放电行波解的存在性。在文献［3］中，作者通过改变α（t）和J（x）的形式而改变h输入，即给h的输入形式一个扰动，分析其对多放电行波解的影响情况。本文主要讨论该模型中行波解对于参数的依赖性，给出其结论完善的证明过程。

1　模型及其参数说明

文献［1］中所研究的Theta模型，当产生激发位势时，如一神经元接近它的阈值，那么它的动力系统会映射为单位圆动力系统，具有形式：

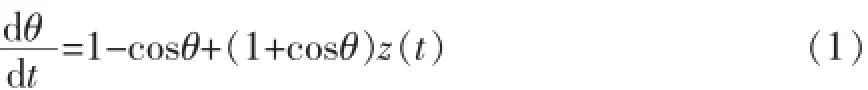
其中θ是相变量，Z（t）表示神经元的所有输入。

如果是单细胞模型，那么（1）式变为：

其中β∈（-1，0）是偏倚参数，控制细胞的兴奋性。I（t）表示神经元依赖于时间的输入。并定义当θ增加时每穿过一次π的奇数倍，就称细胞放电一次。假设没有外部输入，则可得到两个休止态：

其中θrest是稳定的，而θT是不稳定的。

考虑由多个神经元组成的突触耦合网，其计算模型有如下形式：

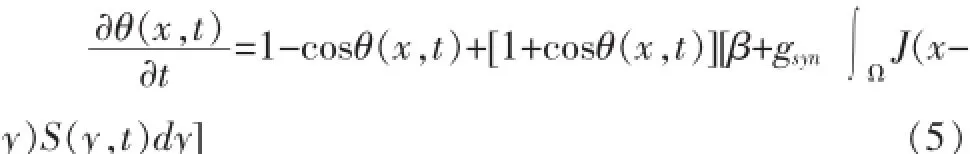
其中（x，t）∈R×R，gsyn表示最大的突触传导系数，J（x）是网络中两细胞间距离的衰减权函数，S（y，t）满足时间的常微分方程［1］。

2　模型假设

用与文献［4］中相同的行波公式，对常速c和ξ=ctx，行波解满足θ（x，t）=θ（ξ），S（x，t）=S（ξ）。由α（t-x/c）=α（ξ/c）可近似得到S。假设每个细胞在ξ=0处放电，细胞在ξ点的网输入是，那么（5）变为：

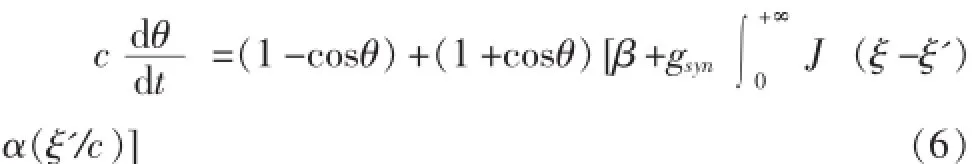
假设J（x）和α（t）具有可积性，且：

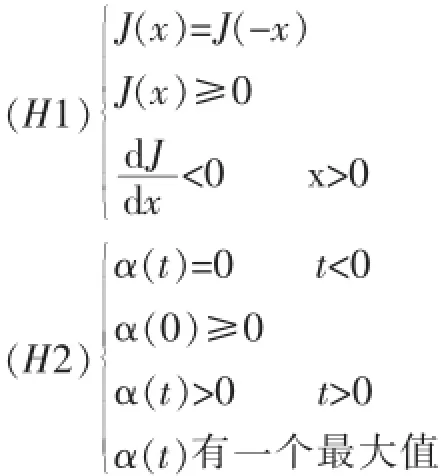
因为模型中的行波解都应满足条件：

且若是单放电行波解还应满足：

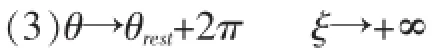
所以以下先在ξ∈（-∞，0］上研究模型，并对满足（H1）和（H2）的α（t）和J（x）的特殊形式加以讨论。

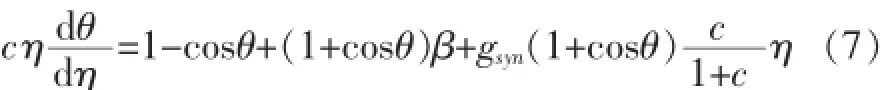
将（7）看作为自治系统：

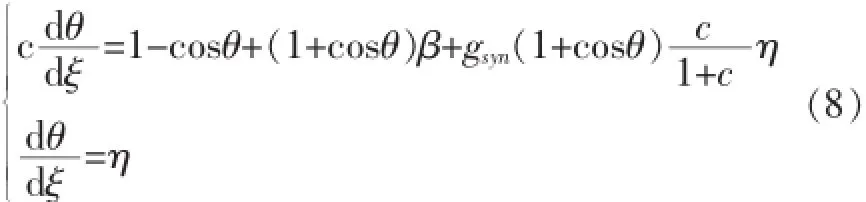
在文献［1］中已证明，自治系统（8）的解（θu（ξ），ηu（ξ））存在，它是穿过（π，1）的不稳定流形的分支｛（θ，η）：θ≥θrest，η＞0｝，且每个细胞都会放电一次以上。对每一个波速c，都存在一点（0，ηa（c））是θ方程的零等倾线的顶点，其中因为行波只有当c使得ηa（c）＜1时才会存在。对这样的c定义θa（c）使得当已证明当c＞0时，θa（c）是c的单调递减函数。下用表示在（8）的流下，不稳定流形的坐标从θa到π的发展时间

3　结论及证明

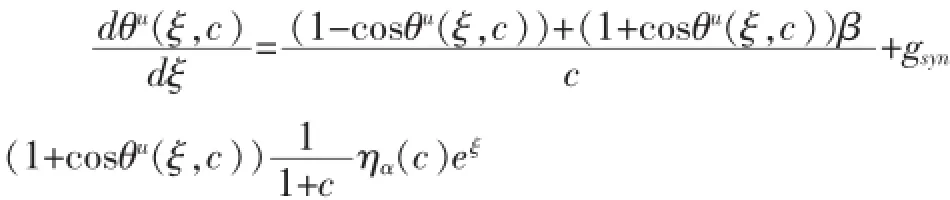
可计算：

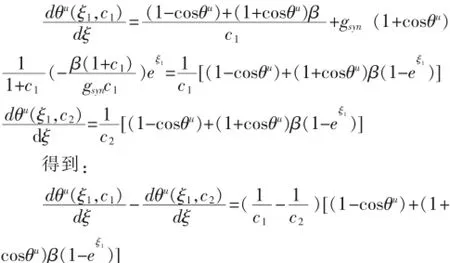
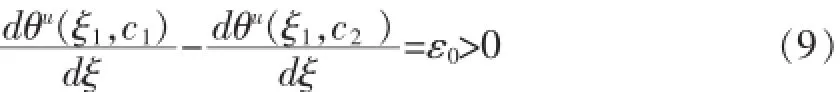
其中ε0＞0是一固定的常数。

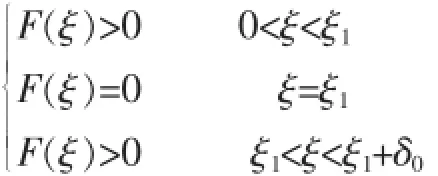
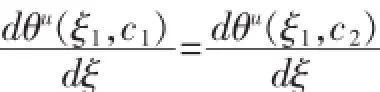
这与（10）式矛盾！

这样，由c1＜c2可得：

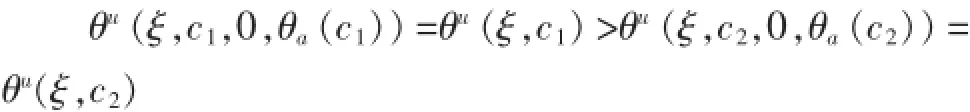
［1］Remus Osan，Jonathan Rubin，and Bard Ermentrout．Regular Traveling Waves in A One-Dimen-Sional Network of Theat Neurons，SIAM J．APPL．MATH．，2002．62．（4）：1197～1221

［2］高菲菲，郝敦元．一维神经网络微分方程模型的研究——多放电行波解的存在性［J］．内蒙古大学学报（自然科学版），2007．38．（4）：361～365

［3］高菲菲，郝敦元．一维神经网络中扰动后多放电行波解存在性［J］．浙江大学学报（理学版），2013，40（4）：391～395

［4］G．B．Ermentrout.The Analysis of Synaptically Generated Traveling Waves.J．Comp．Neurosci．，5（1998）：191～208

［5］G．B．Ermentrout.Type I Membranes，Phase Resetting Curves，and Synchrony.Neural Commput，8（1996）：979～1001

［6］G．B．Ermentrout and N．Kopell，Parabolic Bursting in an Excitable System Coupled with a Slow Oscillation，SIAM J．APPL．MATH．，1986，46（2）：233～253

Theat Model；Traveling Wave Solution；Synaptic Coupling；Dependence

Parameter-Dependence of Traveling Waves Solutions in a One-Dimensional Network of Theta Neurons

GAO Fei-fei
（College of Statistics and Mathematics，Inner Mongolia Universityof Finance and Economics，Hohhot010051）

1007-1423（2015）17-0042-03

10.3969/j.issn.1007-1423.2015.17.009

高菲菲（1981-），女，硕士研究生，讲师，研究方向为微分方程与系统仿真

2015-04-20

2015-05-22

主要研究一维Theta神经元网络的微分方程模型，对该网络模型从神经元生理运动特点和微分方程本身入手进行研究。讨论行波解对于参数的依赖性，即讨论对于固定的突触系数，依赖于速度c的不稳定流形的状态。

Theta模型；行波解；突触耦合；依赖性

内蒙古财经大学校级教育教学项目（No.JX1310）

Discusses the model of differential equations in a one-dimensional network of Theat neurons.Studies the problem from two aspects：the physiological movement characteristics of neurons and the model of differential equations．Discusses parameter dependence of traveling waves solutions in a one-dimensional network of Theat neurons，considers how the behavior of the unstable manifold depends on velocity c for fixed synaptic conductance．