浅谈常微分方程的教学方法

何小燕（内蒙古财经大学统计与数学学院，呼和浩特　010071）

浅谈常微分方程的教学方法

何小燕
（内蒙古财经大学统计与数学学院，呼和浩特010071）

0　引言

常微分方程已经出现了很长时间，所以对它的研究也很漫长，初期主要是求通解，它的解是用初等函数或超函数来表示。在不同的阶段人们选择的方法也是不同的：变量变换解决一阶微分方程是莱布尼茨研究的；积分因子解决是欧拉提出来的.而一些特殊方程如伯努利方程、黎卡蒂方程，是后人为纪念他们的研究成果而名字命名的微分方程。对于一阶常微分方程的初等解法，不仅要掌握的它的自身特点，还应了解其与实际问题的密切联系。通过对初等解法进行归类，可以有条理地进行求解，最起码可以很快判断出所给方程的类型，然后利用各自的特征快速解出结果。不用死记一些解法，更重要的是训练自己思维方法。

1　基本方法的归纳总结

1.1变量分离方程

变量分离形如：

的方程，这里f（x），φ（y）分别是x，y的连续函数。其实这是函数里最简单的一种一阶函数形式。如果φ（y）≠0，我们可将（1）改写成dy=f（x）dx，显然变量φ（y ）已经“分离”出来了，然后给两边同时积分，得：

1.2常数变易方程

（1）线性微分方程定义方程：首先未知函数y和导数y'都是一次的，也就是一阶线性微分方程。

当Q（x）≡0，那么（3）是齐次的，即可分离变量的微分方程。

当Q（x）≠0，那么（3）是非齐次的，求解方法是首先把Q（x）换为0，即：

为（3）的齐次微分方程，其解为 y=ce-∫P（x）dx，这里c是任意常数。（3）的解可利用常数变易法，用u（x）代替

是方程（3）的通解，这里c是任意常数.

此方法比较简便，所以在以后解方程的时候，就可以直接用运（5）式来求解。

（2）伯努利微分方程

①形如

的方程就是伯努利方程P（x），Q（x）都是关于x的连续函数，如果n=0，1时，就是一阶线性微分方程，直接就可用常数变易法求得结果。对于y≠0，在方程（6）两边同乘y-n，得：

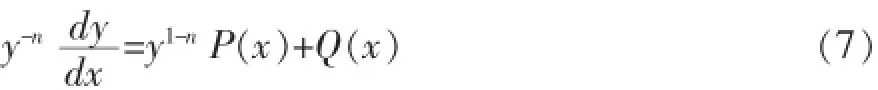
引入变量变换：

从而：

将（8），（9）代入（7），得到：

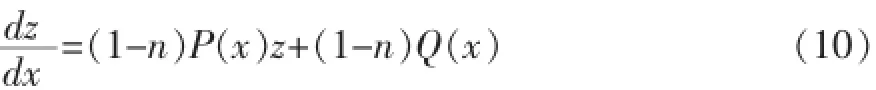
为一阶线性微分方程而且是非齐次线性微分方程，就可利用（5）求得它的通解：

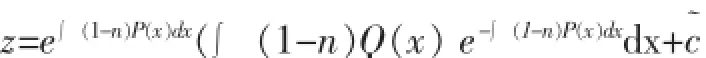
然后将原来的变量代入，得到的便是（6）的通解.这里不要忘了在n＞0时，还有y=0的解。

（2）伯努利微分方程的解题步骤可以有以下：

①两端同乘（1-n）yn；②代换z=y1-n；③解关于z的线性微分方程；④还原。

1.3恰当微分方程求解

说明一下 φ（y）是 y的任意可微函数，现要求有

由此：

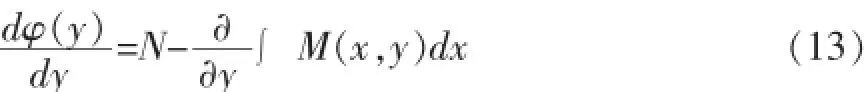
又因为：

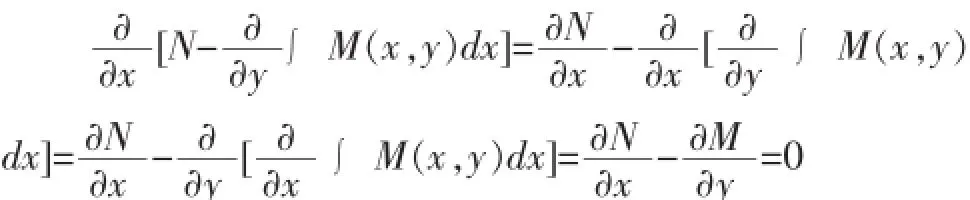
再对（13）关于y积分，得到：

将（14）代入（12），可得：

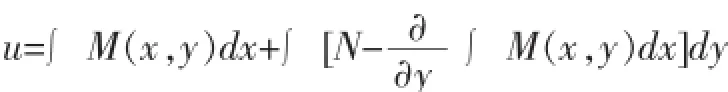
所以，恰当微分方程（11）的通解就是：

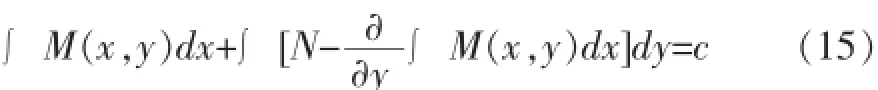
这里c是任意常数。

1.4积分因子法

则称μ（x，y）为方程（11）的积分因子。

这时v（x，y）=c是（17）的通解，因此也就是（16）的通解［2］。

①观察法

求积分因子的最早方法就是观察法，主要目的就是凑成恰当微分方程，因为简单明了，当我们遇到例题时再做进一步解说。

②公式法

要使函数μ（x，y）为（16）的积分因子，则其充要条件是即：

（3）分组法

分组法针对的就是一类较复杂的微分方程，因为它们难用观察法和公式法直接求出，这时找积分因子就需要运用分组积分因子法。

2　结语

以上是对一阶常微分方程的初等解法技巧的几种解法的总结，希望学生可以熟悉各种类型方程的解法，并正确而又快捷地判断所给出的方程属于何种类型，从而按照所掌握的方法进行求解.但实际所遇见的方程未必都恰好是所介绍的，所以学生在学习的过程中要多注意学习解题的技巧，学会举一反三，以不变应万变，尤其能结合计算机去解决一些复杂难算的问题，这样我们就可以掌握学习中的许多乐趣，也可以轻松解决一些问题。

［1］王高雄，朱思铭，周之铭，王寿松，李艳会.常微分方程（第三版）［M］.北京：高等教育出版社，2006.

［2］龚雅玲.求解微分方程的积分因子法［J］.南昌教育学院学报，2007（01）.

［3］温启军，张丽静.关于积分因子的讨论［J］.长春大学学报，2006（10）.

［4］华东师范大学数学系.数学分析（第四版）［M］.北京：高等教育出版社，2010.

［5］汤光宋，余复民.应用交换变量位置法解两类一阶常微分方程［J］.兰州工业高等专科学校学报，1996（1）：20-25.

Ordinary Differential Equation；Variable Separation Method；Constant Variation Method；Integral Factor Method

Discussion on the Teaching Mode of Ordinary Differential Equation

HE Xiao-yan
（Inner Mongolia Institute of Finance and Economics，Hohhot 010071）

1007-1423（2015）23-0059-04

10.3969/j.issn.1007-1423.2015.23.014

何小燕（1983-），女，内蒙古人，硕士研究生，讲师，研究方向为非线性动力学与控制

2015-07-03

2015-08-10

常微分方程是数学专业必修的专业基础课之一，是数学分析、高等代数和解析几何的应用于发展。在讲授一阶微分方程求解的过程中，有多种求解方法与技巧。根据多年教学经验，归纳总结给出求解一阶微分方程的基本方法，如一变量分离法、常数变易法、恰当微分方程以及积分因子法等，便于学生更好地了解和掌握一阶微分方程的初等解法。

常微分方程；变量分离法；常数变易法；积分因子法

Ordinary differential equations is one of the required professional course for professional mathematics，and the application and development of the mathematical analysis，higher algebra and analytic geometry.In the process of learning of one order differential equation，there are many solving methods and techniques.Gives the general separation of variables，constant variation method，exact differential equation and the basic ways of integrating factor method，presents the basic method of application，so convenient we better understand their own characteristics.