一种基于星载多波束天线的单星干扰源定位方法*

余 强，谢智东，张更新

0 引言

近年来，由于各国卫星通信业务的迅速增长，轨道与频率资源日趋紧张，卫星所处电磁环境日益恶化，通信卫星受干扰事件屡见不鲜，造成了诸多恶劣影响和大量经济损失。迅速准确地确定干扰源的空间位置并采用适当手段来消除其影响，是现代卫星通信系统的一项基本电子防护要求。卫星通信系统实现干扰源定位主要有两种途径，一是基于信号参数到达差(TDOA 或 FDOA)定位［1－3］，二是基于信号到达角(DOA)定位，即测向定位［4－6］。对于 GEO卫星通信系统，系统中一般仅包括有限的几颗卫星，大多数情况下只有一颗卫星或者选择邻星比较困难，因此难以通过到达时差(TDOA)和到达频差(FDOA)等基于双星或三星的定位技术实现干扰源定位;而基于测向定位的单星定位技术，由于受到星载测向设备以及卫星运行轨道的限制，在应用中也存在各种问题，所以有必要找到一种技术相对简单的基于单星的干扰源定位方法。

对于采用大型展开式多波束天线的GEO移动卫星通信系统，利用多波束天线各点波束在同一个干扰源位置上具有不同增益的特点，结合天线方向图分布实现干扰源定位是一个新思路。日本的研究人员曾经做过类似的实验，他们提出了通过比较各个波束接收的干扰信号幅度进行测向定位的方案，并在工程实验卫星(ETS－VI)上进行了实验，但其定位精度不高(测向误差达±0．21度，相应的地面定位误差为131 km)［7］。

本文针对卫星多波束天线七波束复用的情形，利用三个相邻的同频波束接收并估计干扰源信号的强度，通过求解三个波束的等信号强度曲线的交点确定固定干扰源在地面的位置。

1 定位过程

1． 1 原理描述

多波束天线具有高灵敏度，点波束旁瓣值较高，邻近波束之间有较大的重叠区域。因此，当系统受到干扰时，除主要受干扰波束接收到干扰信号外，其邻近波束也会接收到该信号。根据多波束天线方向图的分布特性，各点波束在干扰源方向上的天线增益不同，使得各波束所接收到的信号强度有较大的差异。干扰源定位系统实时监测卫星反向链路信号，一旦出现干扰，利用干扰信号较强的特点，就能在某个点波束中快速发现干扰，并确定其它主要受干扰点波束，对干扰信号进行多维认知，获得干扰信号强度在多波束环境下的空间分布特性，结合由多波束天线方向图地面投影模型获取的天线增益，即可实现对干扰源的定位。在星载多波束天线采用七波束复用时，其定位原理示意图如图1所示。

假如地面覆盖区B所在的波束受到地面辐射源的恶意干扰，此时至少有两个相邻的同频波束可以接收到该干扰源的信号，其地面覆盖区为图1中的A和C，D为待定位干扰源位置。首先，干扰源D发出的信号到达卫星三个同频波束获得不同的增益，由于波束中心坐标已知，卫星坐标可以由卫星星历获取，则通过计算波束中心点和干扰源位置点同卫星连线之间的夹角θ，结合天线方向图，可以得到三个受干扰波束分别对应的星上增益;其次，定位系统在确定主受干扰波束并选择相邻受干扰波束之后，对各受干扰波束接收到的干扰信号进行强度估计;最后，通过卫星系统的监测获取该干扰信号到达卫星受到的损耗值，就可以得到三个关于干扰信号链路计算的方程，联立干扰源位置坐标的约束条件就可以解得待定位干扰源的位置。

图1 单星干扰源定位原理示意Fig．1 Position principle by single satellite

1． 2 天线方向图及其数学模型

实际星上接收天线通常为赋形天线，与抛物面天线类似，可以建立方向图表示增益与偏离波束中心指向角度的关系，但通常不能表达为解析关系，只能以数据库的形式表示。实际工程应用中，进行干扰源定位之前都要对天线方向图的地面投影模型进行测量与校正，建立每个点波束的天线方向图(包括旁瓣)模型，实现与地球上的地理位置关联，并以数据库的形式存储起来。

对于圆形波束，文献［8］提出一种通过用户发射信号入射方向与波束中心之间的夹角近似计算波束增益的方法。假设点波束中心增益为G0，那么用户与波束之间的波束增益G近似计算为:

式中，u=2．07123sin(θ)/sin(θ3dB)，J1和 J3分别是1阶和3阶第一类贝塞尔函数，θ3dB是天线增益相对波束中心3 dB衰减处所对应的角度，θ表示用户发射信号入射方向与点波束中心之间的夹角。

假设卫星天线口径D为12．5 m，信号的载波频率为2 GHz，即信号波长λ为0．15 m，则半功率波束宽度 θ3dB=70·λ/D=0．84(度)。

当θ=0时，卫星天线增益如式(2)所示:

取天线效率 η为 0．5，则波束中心增益为45．35 dBi。此时，入射信号偏离波束中心的角度与波束增益之间的对应关系如图2所示。

图2 入射信号角度与波束增益的关系Fig．2 Relationship of between incident angle and antenna gain

1． 3 定位方程组的建立

考虑圆形波束覆盖的情形，在计算中以用户发射信号入射方向与波束指向中心之间的夹角θ为媒介建立干扰源位置坐标与对应星上接收天线增益的关系。

例如，在图1中，卫星和波束A中心点坐标均已知，假设在空间直角坐标系下分别为向量rS和rA，干扰源位置坐标设为rD=(x，y，z)，根据余弦定理，干扰源与卫星连线偏离波束A中心点与卫星连线的夹角θA可以用式(3)表示。

由1．2节中天线方向图函数的表达式，可以进一步得出，干扰源方向对应星上天线该波束的增益为G(θA)。同理，可以分别得到干扰源方向对应星上波束B和波束C的增益G(θB)和G(θC)。

当干扰源定位系统在反向链路监测到干扰时，利用干扰信号强弱关系确定主受干扰波束及其相邻同频波束后，对各波束接收的干扰信号强度进行估计。这里假设在星上各波束接收干扰信号强度分别为uA，uB和uC，信号的在传播过程中的损耗假设为uf，地面干扰源的初始辐射强度设为t，则关于波束A接收的干扰信号强度uA可以表示为:

整理得:

式中，Δu=t－uf。同理可得关于波束B和C的链路计算方程:

地面干扰源位置向量rD满足球面方程:

联立式(5)、式(6)、式(7)并将θ代入得到定位方程组:

求解该四元非线性方程组即可得到地面干扰源的位置。分析方程组(8)可知，Δu不影响干扰源位置坐标的求解，即干扰源的辐射强度t和信号在传播过程中的损耗uf不影响实际定位结果，但为方便仿真分析，在下文中仍将进行假设。

2 仿真验证

考虑到定位方程组的特殊性，本文采用蒙特卡罗算法并结合网格法的思想求解。

首先，构造约束函数:

然后，在三个定位波束中心点坐标范围内随机产生未知分量x和y，利用约束条件(7)计算分量z，并在合理范围内随机产生未知分量Δu，最后将该随机解代入方程组计算约束函数值，如此反复搜索，直至产生的随机解(xi，yi，zi，Δui)令约束函数值E(xi，yi，zi，Δui)足够小并达到定位精度要求为止。当然，这个过程随着搜索次数的增加花费的时间也随着增加。为加速搜索，降低计算量，根据网格法的思想，在搜索到一定精度的解之后，则以该点为中心，在较小半径的解空间内进行第二次随机搜索，直至搜索到满足精度要求的解。

仿真中，假设受干扰波束中心点经纬度分别为:E116°23'N39°54'(北京)、E104°04'N30°45'(成都)和 E119°17'N26°05'(福州)，星下点经纬度为 E113°53'N29°58'(武汉)，卫星轨道高度为35 786 km，地球半径 为6 371 km。对经纬度分别为 E113°53'N29°58'、E115°53'N28°41'、E116°23'N38°48'的地面干扰源进行定位仿真，搜索次数分别为104、105和106，仿真次数为100，定位仿真误差结果如表1所示。

其中对第一个目标位置定位的结果示意图如图3～5所示，图中五角星代表干扰源真实位置，定位误差曲线如图6所示。

图3 104次搜索定位结果Fig．3 Position result of 104 search

图4 105次搜索定位结果Fig．4 Position result of 105 search

图5 106次搜索定位结果Fig．5 Position result of 106 search

由表1中的数据可以看出，本文提出的基于星载多波束天线的单星干扰源定位方法是有效的，在没有测量误差的理想情况下，其定位精度可以达到km量级。图6进一步说明了文中采用的搜索算法的收敛性，并且随着搜索次数的进一步增加或者搜索方法的改良，其定位精度还有上升的空间。

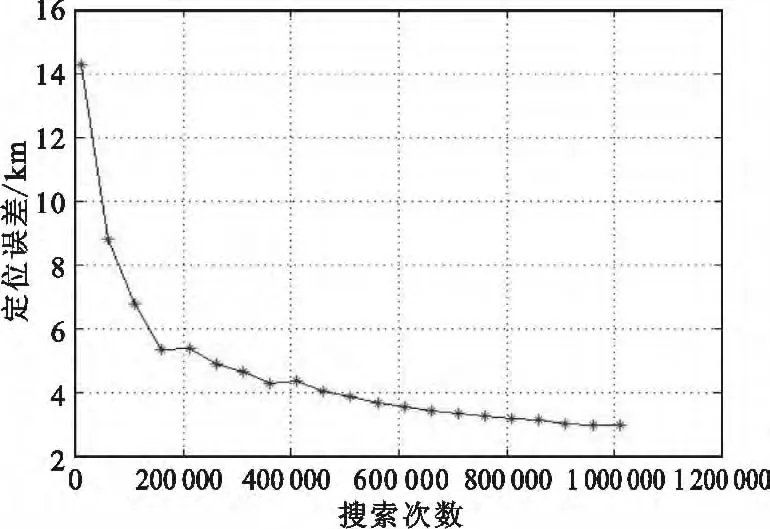
图6 定位误差曲线Fig．6 Position error curve

表1 不同搜索次数下的平均定位误差(km)Table 1 Mean position error(km)under different search times

3 结语

基于星载多波束天线的单星干扰源定位技术具有成本低、技术相对简单的优点，在定位精度要求不高的应用场合具有较强的竞争力，不仅可以作为独立手段协助排除地面干扰源，其定位结果还可以用来引导低轨侦察卫星进行更加精确的定位。当然，该方法的定位精度依赖于多波束天线方向图的测量精度以及多波束环境下干扰源信号强度的估计精度等因素，各种误差因素对定位精度的影响以及相应的补偿措施也需要进一步研究，因此该方法离实际应用还有较长的一段路要走。

［1］ 丁宏毅，柳其许，王巍．Chan定位算法与TDOA估计精度的关系［J］．通信技术，2010，43(03):134－136．DING Hong － yi，LIU Qi－ xu，WANG Wei．Relation Between Chan Location Algorithm and TDOA Estimation Accuracy［J］．Communications Technology，2010，43(03):134:136．

［2］ YU Hua－gang，HUANG Gao－ming．Approximate Maximum Likelihood Algorithm for Moving Source Localization Using TDOA and FDOA Measurements［J］．Chinese Journal of Aeronautics，2012(25):593 －597．

［3］ ZHANG Wei，ZHANG Geng － xin，HU Jing．Research on Priori Information of TDOA/FDOA in Satellite Communication Based on Ephemeris of Satellite［C］//ICSPCC:Xi＇an:IEEE，2011:413:417．

［4］ 焦健．卫星通信系统干扰源DOA估计方法研究［D］．哈尔滨:哈尔滨工业大学，2008．

JIAO Jian．Research on DOA Estimation of the Interference Sourses in Satellite Communication System［D］．Harbin:Harbin Institute of Technology，2008．10．

［5］ 刘海军，叶浩欢，柳征，等．基于星载干涉仪侧向的辐射源定位综合算法［J］．国防科技大学学报，2009，31(06):110－114．

LIU Hai－jun，YE Hao－huan，LIU Zheng，et al．Integration Algorithm of Emitter Location Based on Satelliteborne Interferometer［J］．Journal of National University of Defense Technology，2009，31(6)

［6］ 李献斌．单星测频无源定位技术研究［D］．长沙:国防科技大学，2009．

LI Xian－bin．Research on Passive Positioning System of Single－Satellite Frequency－Measurement［D］．Changsha:National University of Defense Technology，2009．

［7］ Y．Matsumoto，M．Tanaka，H．Okazawa，et al．Satellite Interference Location System Using On－board Multibeam antenna［J］．Electronics and Communications in Japan，1997，80(11):1022 －1030．

［8］ C．Caini，G．E．Corazza，G．Falciasecca，M．Ruggieri，et al．A Spectrum － and Power－Efficient EHF Mobile Satellite System to be Integrated with Terrestrial Cellular Systems［J］．IEEE Journal on Selected Areas in Communications，1992，(10)8:1315 －1325．